अप्राचलात्मक पद्धति : एखाद्या समष्टीच्या (म्हणजे माणसे, प्राणी, वस्तू इ. प्रकारच्या अथवा विविध वैज्ञानिक निरीक्षणांच्या कोणत्याही समूहाच्या) एखाद्या गुणधर्माबद्दल (उदा., कर्करोगग्रस्त माणसांचे प्रमाण) माहिती मिळविण्यासाठी त्या समष्टीतून काही जणांचा प्रतिदर्श (नमुना) घेऊन व त्याचे सांख्यिकीय सिद्धांतांच्या आधारे विश्लेषण करून त्या समष्टीसंबंधी अनुमाने काढण्यात येतात. अशी अनुमाने काढण्याच्या विविध पद्धतींपैकी अप्राचलात्मक वा अप्रचलात्मक पद्धती या काही पद्धती आहेत.
बऱ्याचशा सर्वसाधारण सांख्यिकीय कसोट्यांमध्ये समष्टीच्या ज्ञात किंवा गृहीत धरलेल्या वंटन फलना- तील[→ वंटन सिद्धांत] प्रचलांच्या (विशिष्ट परिस्थितीत अचल राहणाऱ्या राशींच्या उदा., सरासरी, माध्य इ.) मूल्यांचे आकलन (अंदाज) करणे किंवा दोन प्रतिदर्श एकाच समष्टीतील आहेत की नाहीत याची कसोटी घेणे, अशा स्वरूपाचे उद्देश असतात. अशा कसोटीच्या पद्धती प्रचलांशी संबंधित असल्यामुळे त्यांना प्रचलात्मक पद्धती म्हणतात. याउलट कित्येक वेळा समष्टीतील वंटनासंबंधी कोणतीही अटकळ करणे शक्य वा उचित नसते किंवा अभ्यासकाला त्यात स्वारस्यही नसते. अशा प्रकारच्या सांख्यिकीय प्रश्नांत प्रचलांना स्थान नसल्यामुळे, त्यांचा ज्या विशिष्ट पद्धतींनी अभ्यास करण्यात येतो त्यांना अप्रचलात्मक किंवा वंटनमुक्त्त पद्धती म्हणतात. अशा प्रकारच्या पुष्कळशा पद्धतींत समष्टीचे वंटन फलन संतत आहे एवढेच गृहीत धरले जाते. यांपैकी काही पद्धतींचे खाली विवेचन केलेले आहे.
कॉल्मॉगॉरॉव्ह-स्मिर्नॉव्ह कसोट्या : एखाद्या प्रतिदर्शातील निरीक्षणे समष्टीबद्दल अटकळ बांधलेल्या वंटनाशी सुसंगत आहेत की नाहीत हे पुढीलप्रमाणे पडताळून पाहता येते. समजा, गृहीतकानुसार समष्टीचे वंटन फलन फ (क्ष) आहे आणि क्ष१, क्ष२, …..,क्षप अशी प निरीक्षणे असलेल्या प्रतिदर्शाचे निरीक्षित फलन (म्हणजे क्ष पेक्षा कमी मूल्य असणाऱ्या निरीक्षणांची संख्या देणारे फलन) फप (क्ष) आहे. क्ष ला शक्य ती सर्व मूल्ये देऊन मिळणाऱ्या | फप (क्ष)-फ (क्ष) | या फलनाच्या महत्तम मूल्याला दप म्हणू. गृहीत आणि निरीक्षित वंटनांमधील तफावतीची दप वरून चांगली कल्पना येऊ शकते. दप चे मूल्य प्रसंभाव्यत: सार्थ असण्याइतके मोठे असेल तर निरीक्षित प्रतिदर्श गृहीत धरलेल्या समष्टीतून आलेला असणे संभवत नाही असे म्हणावे लागेल. फ (क्ष) हेच समष्टीचे वंटन फलन आहे असे गृहीत धरून काढलेल्या दप च्या वंटनावरून आणि त्यावर आधारलेल्या कोष्टकांवरून निरीक्षित दप चे मूल्य सार्थ आहे की काय हे ठरविता येते. प ही संख्या बरीच मोठी असेल तर दप चे वंटन खालील सूत्राने मिळते :
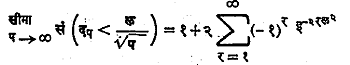
(येथे इ हा स्वाभाविक लॉगरिथमाचा आधारांक आहे. ल > ०).
दिलेले दोन प्रतिदर्श एकाच समष्टीतून आलेले आहेत की काय हे ठरविण्याचीही वरील प्रकारची कॉल्मॉगॉरॉव्ह-स्मिर्नॉव्ह कसोटी आहे. समजा, दिलेल्या प्रतिदर्शांतील निरीक्षणे अनुक्रमे प आणि म आहेत व त्यांची निरीक्षित वंटन फलने फप(क्ष) आणि फम(क्ष) अशी आहेत. तसेच समजा
| द | = | महत्तम | | फप (क्ष) – फम (क्ष) | . |
| ( क्ष ) |
जर प आणि म या संख्या मोठ्या असतील तर द चे वंटन खालील सूत्राने मिळते.
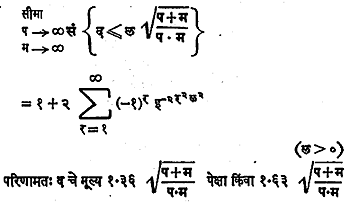
पेक्षा जास्त असेल तर अनुक्रमे ५% व १% सार्थता पातळींवर दोन्ही प्रतिदर्श एकाच समष्टीतून आलेले आहेत हे गृहीत त्याज्य मानावे लागते. अशाच कसोट्या म आणि प या संख्या लहान असताना वापरण्यासाठी कोष्टके उपलब्ध आहेत.
मालिका कसोटी : समजा दोन प्रतिदर्शांतील निरीक्षणे वाढत्या मूल्यांनुसार क्ष१, क्ष२, ……,क्षम आणि य१,य२…..,यप अशा क्रमाने लावली आहेत आणि समजा या सर्वांचा मिळून वाढत्या मूल्यांनुसार
क्ष१, क्ष२ य१ क्ष३ य२ य३ य…क्ष४ क्ष५…… ……………………………….(अ )
असा क्रम लागतो. या क्रमात जर दोन क्ष अक्षरांमध्ये नुसत्या य अक्षरांचीच किंवा दोन य अक्षरांमध्ये नुसत्या क्ष अक्षरांचीच पुनरावृत्ती होत असेल तर अशा अखंड पुनरावृत्तीला मालिका म्हणतात आणि अशा भिन्न अक्षरांमधील समान अक्षरांच्या संख्येला त्या मालिकेची लांबी म्हणतात. जर दोन्ही प्रतिदर्श एकाच (किंवा एकच वंटन असलेल्या) समष्टीतून आलेले असतील तर त्यातील क्ष-मूल्ये आणि य-मूल्ये एकमेकांत चांगली मिसळलेली आढळतील. यामुळे (अ) मधील मालिका सामान्यत: कमी लांबीच्या व म्हणून संख्येने जास्त येतील. याउलट एका समष्टीचे माध्य (सरासरी) दुसरीच्या माध्यापेक्षा बरेच कमी असेल तर त्या प्रतिदर्शा- तील पुष्कळशी मूल्ये (अ) मध्ये सुरुवातीलाच आणि दुसऱ्या प्रतिदर्शाची बरीच मूल्ये शेवटाला आढळतील. यामुळे (अ) मधील मालिका जास्त लांबीच्या व म्हणून संख्येने कमी येतील. तसेच दोन्ही समष्टींची माध्ये एक असूनही एका समष्टीचे अपस्करण दुसरीपेक्षा बरेच जास्त असेल तर पहिल्या प्रतिदर्शाची पुष्कळशी मूल्ये (अ) मध्ये सुरुवातीला आणि शेवटाला पसरलेली व दुसरीची मधल्या भागात केंद्रीत झालेली आढळतात व त्यामुळे पुनः मालिका जास्त लांबीच्या आणि संख्येने कमी आढळतील. म्हणूनच मालिकांची एकूण संख्या र ही (सार्थतेच्या दृष्टीने) फारच कमी (समजा, ≥ र°) झाली, तर ते मूळ समष्टी एकच वेगळ्या असल्याचे निदर्शक मानावे लागेल. दोन्ही समष्टी एकच असण्याच्या गृहीतकानुसार (अ) मधील मालीकांची संख्या र असण्याची संभाव्यता पुढील सूत्रांनी मिळते :
र= समसंख्या २ क असल्यास

विचरण असलेले प्रसामान्य वंटन असल्याचे मानता येते आणि त्यानुसार नेहमीच्या कसोट्या लावता येतात.
एखाद्या प्रतिदर्शाच्या यदृच्छतेची व त्यातील मूल्यांच्या निरवलंबतेची कसोटीही वरील प्रकारच्या मालिका-संख्येवर आधारता येते. समजा प्रतिदर्शातील मूल्ये क्ष१, क्ष२,…, क्षप या क्रमाने मिळालेली आहेत ती मध्यस्थ मूल्यापेक्षा कमी वा अधिक असल्यास अनुक्रमे अ किंवा क अशी लिहीत गेल्यास
क अ अ क अ अ अ अ क क अ क….
अशासारखी श्रेणी मिळेल. या श्रेणीतील अ आणि क यांच्या मालिकांची एकूण संख्या र असेल ती यदृच्छ प्रतिदर्शाच्या बाबतीत र चे माध्य व त्याचे विचरण अनुक्रमे
| प | + १आणि | प(प-२) |
| २ | ४(प-१) |
या सूत्रांनी मिळते. प ही संख्या मोठी असेल ती र चे वंटन जवळजवळ प्रसामान्य राहते व त्यामुळे नेहमीच्या कसोट्या लावता येतात.
चिन्ह कसोटी : समजा, एखाद्या समष्टीच्या वंटनाचे मध्यस्थ मूल्य म आहे किंवा काय हे त्या समष्टीतील पनिरीक्षणे असलेल्या प्रतिदर्शावरून ठरवावयाचे आहे. म हे मध्यस्थ मूल्य असेल तर प्रतिदर्शातील एखादे मूल्य मपेक्षा जास्त किंवा असण्याची संभाव्यता प्रत्येकी १/२ होईल. म्हणजेच प्रतिदर्शातील म पेक्षा जास्त असलेल्या मूल्यांची संख्या क असेल तर क चे वंटन प्रत्येकी (१/२+१/२)प या द्विपदाप्रमाणे होईल. यावरून क चे प्रत्यक्ष मिळालेले मूल्य सार्थ (आणि म्हणून गृहीतक त्याज्य) आहे की काय हे ठरविता येईल. प ही संख्या मोठी असल्यास अर्थात क चे वंटन जवळजवळ प्रसामान्य वंटनानुसार होईल. प्रत्यक्षात म पेक्षा अधिक असलेल्या प्रत्येकमूल्याकरिता + चिन्ह आणि कमी असल्यास-चिन्ह मांडले जाते (एखादे मूल्य म एवढेच असल्यास तेप्रतिदर्शातून वगळण्याचा एक पर्याय आहे). अशा +चिन्हांची संख्या म्हणजेच वर उल्लेखिलेली क ही संख्या होय. म्हणूनच या कसोटीला चिन्ह कसोटी म्हणतात. ही कसोटी वापरण्यास सोपी व सुलभ असते.
दोन चरांचे वंटन एकच आहे की काय हे ठरविण्यासाठीही वरील कसोटीचा उपयोग होतो. उदा., समजा सामान्य ज्ञानासंबंधीच्या एका शिक्षणक्रमाच्या उपयुक्ततेची चाचणी घ्यावयाची आहे. समजा प उमेदवारांच्या या शिक्षणक्रमापूर्वी व तदनंतर परीक्षा घेतल्या आहेत व त्यांचे त्यांतील गुण अनुक्रमे क्ष१, क्ष२,….क्षप आणि य१,य२,…यप असे आहेत. या शिक्षणक्रमाचा काहीच उपयोग नसेल, ती क्ष पेक्षा य कमी वा जास्त असण्याची संभाव्यता तितकी म्हणजे १/२ राहील व म्हणून (क्ष-य)चे चिन्ह + किंवा – असण्याची संभाव्यता १/२ राहील म्हणून (क्ष१-य१), (क्ष२-य२),…, (क्षप-यप) या समूहात धन चिन्हांची संख्या क असल्यास क चे वंटन (१/२+१/२ ) प या द्विपदाप्रमाणे होईल. यावरून प्रत्यक्ष मिळालेले क चे मूल्य सार्थ (व म्हणून क्ष आणि य मध्ये काहीच फरक नसल्याचे गृहीतक त्याज्य) आहे की नाही हे वरीलप्रमाणे ठरविता येईल. अशाच प्रकारच्या दोन परस्परा- वलंबी किंवा निरवलंबी चरांना याच प्रकारचे विवेचन व कसोटी लावता येईल. मात्र यासाठी दोन्ही चरांच्या निरीक्षणांची संख्या एकच असणे जरूर आहे. नाही तर काही निरीक्षणे गाळावी लागून वाया जातील.
विल्कॉक्रसन चिन्हांकित कोटी कसोटी : वर दिलेल्या चिन्ह कसोटीतील (क्ष-य) ह्या चराच्या चिन्हाबरोबरच त्याच्या मूल्यांचाही विचार करणारी जास्त कार्यक्षम कसोटी विल्कॉक्रसन यांनी दिलेली आहे. समजा वरील उदाहरणातील (क्ष-य) च्या चिन्हविरहित मूल्यांची वाढती कोटी लावली व अशा प्रत्येक कोटीला त्या त्या मूल्याचे चिन्ह (+ किंवा −) लागू केले तर वरील गृहीतकानूसार धन-चिन्हांकित कोटींची बेरीज आणि ऋण-चिन्हांकित कोटींची बेरीज जवळजवळसारख्या यावयास पाहिजेत, एक बेरीज दुसरीपेक्षा फारच कमी वा जास्त झाल्यास गृहीतक त्याज्य मानावे लागेल. प ही संख्या २५ पर्यंत असल्यास या कसोटी- साठी कोष्टके उपलब्ध आहेत. एरवी वरील बेरजांपैकी कमी असलेली बेरीज ही
प (प+१) हे माध्य आणि प(प+१)(२प+१)
———— ————-
४ २४
हे विचरण असलेल्या प्रसामान्य स्वरूपाचे वंटन आहे असे धरून नेहमीच्या कसोट्या लावता येतात.
मध्यस्थ कसोटी : समजा, क्ष आणि य ह्या चरांची अनुक्रमे प आणि म निरीक्षणे उपलब्ध आहेत व दोन्ही चरांची वंटने (किंवा निदान त्यांची मध्यस्थ मूल्ये म्हणजे आकारमानानुसार निरीक्षणे क्रमवार लावल्यानंतर मध्यभागी येणारी मूल्ये) एकच आहेत असे गृहीतक आहे.समजा प+म निरीक्षणांचा मिळून क्ष१, क्ष२, …, झप+म असा वाढत्या मूल्यांनुसार क्रम लावलेला आहे व त्यात क्षल हे मध्यस्थ मूल्य आहे. वरील अनुक्रमात क्षल पेक्षा कमी असलेल्या क्ष-मूल्यांची संख्या क आणि य-मूल्यांच्या संख्या ख असण्याची संभाव्यता वरील गृहीतकानुसार
| ( | प | ) | ( | म | प+म | ) | |
| क | ख | ल |
अशी येते. यावरून क आणि ख यांची निरीक्षित मूल्ये सार्थ (आणि म्हणून गृहीतक त्याज्य) आहेत की काय हे ठरविता येते. प आणि म या संख्या मोठ्या असल्यास क चे वंटन प/२ हे माध्य आणि पम/(प+म-१) हे विचरण असलेल्या प्रसामान्य वंटनाच्या स्वरूपाचे येते व यावरून नेहमीच्या कसोट्या लावता येतात.
मान-व्हिटनी- विल्कॉकसन कसोटी : समजा, क्ष आणि य ह्या चरांची अनुक्रमे प आणि म निरीक्षणे वरीलप्रमाणे एकत्र करून वाढत्या मूल्यांनुसार मांडली आहेत. त्यातील य-मूल्यांच्या कोटींची बेरीज र येते आणि समजा
| स= म प + | म (+१) | − | र, |
| २ |
तर क्ष आणि य यांची वंटने असल्यास आणि प व म या संख्या मोठ्या (८पेक्षा जास्त ) असल्यास स चे वंटन,१/२म प हे माध्य आणि म. प (म+प+१)/१२ हे विचरण असलेल्या प्रसामान्य वंटनासारखे येते. यामुळे गृहीतकाच्या त्याज्यतेच्या किंवा ग्राह्यतेच्या योग्य त्या नेहमीच्या कसोट्या लावता येतात. या कसोटीला ‘कोटि-योग कसोटी’ किंवा ‘यू-कसोटी’ असे म्हणतात.
गृहीतकांच्या वर निर्देशिलेल्या बहुतेक कसोट्या नेहमीप्रमाणे पर्यायाच्या स्वरूपानुसार योग्य त्या वारंवारता-वक्राच्या वामपुच्छावर, दक्षिणपुच्छावर किंवा उभय पुच्छांवरही आधारता येतात.
मध्यस्थ मूल्याच्या विश्वास सीमा : एखाद्या चराच्या समष्टीतील इष्ट विश्वासांकाच्या सीमा अप्रचलात्मक पद्धतींनी काढणे शक्य असते. समजा, उपर्युक्त मध्यस्थ म आहे आणि प्रतिदर्शातील मूल्ये वाढत्या क्रमाने क्ष१, क्ष२, …, क्षप अशी आहेत. तर कोणत्याही निरीक्षणाचे मूल्य म पेक्षा कमी (वा जास्त) असण्याची संभाव्यता १/२ आहे. हे लक्षात घेऊन द्विपद वंटन लावल्यास

असे आढळून येते. यातील उजव्या बाजूचे मूल्य त येत असेल तर क्षर आणि क्षस या म च्या त विश्वासांक असलेल्या सीमा होत. र आणि स ची मूल्ये योग्य अशी घेतल्यास म च्या इष्ट त्या (किंवा त्या आसपासच्या) विश्वासांकाच्या क्षर आणि क्षस या सीमा मिळू शकतील.
चराच्या निरवलंबतेच्या कसोट्या : एखाद्या प्रतिदर्शातील निरीक्षणांचे अ या गुणानुसार अ१, अ२, …, अर या वर्गामध्ये आणि क या गुणानुसार क१, क२, …, कस या वर्गामध्ये वर्गीकरण होत असल्यास हे दोन गुण निरवलंबी आहेत की ते सहसंबंधित आहेत, याची कसोटी घेण्यासाठी काय-वर्ग कसोटी वापरतात
[→सांख्यिकीयअनुमानशास्त्र]. उदा., धूम्रपान व कर्करोग यांमध्ये काही सहसंबंध आहे की काय हे अजमावण्यासाठी ही कसोटी वापरता येईल. या कसोटीशिवाय दोन गुणांचे किंवा चरांचे सहविचरण मोजण्यासाठी आणि त्यावरून समष्टीविषयी अनुमान काढण्यासाठी स्पीअरमन व केंड्ल यांनी सुचविलेल्या कोटि-सहसंबंधांकावर आधारलेल्या रीतीही उपलब्ध आहेत.अप्रचलात्मक पद्धतींखाली येणाऱ्या बऱ्याच उपलब्ध पद्धतींपैकी काहींचे वर थोडक्यात विवेचन केलेले आहे. या पद्धती बहुतांशी स्वयंप्रेरणेवर आधारलेल्या आहेत. पण त्या जास्त शास्त्रशुद्ध पायांवर उभारण्याचे संशोधकांचे प्रयत्न चालू आहेत.
संदर्भ : 1. Fraser, D. A. Non-Parametric Methods in Statistics, New York, 1957.
2. Harvard University Press. Bibliography of Non-Parametric Statistics, 1962.
3. Walsh, J. E. Handbook of Non-Parametric Statistics, Princeton, 1962.
नाडकर्णी , प्र. ना.