अन्वस्त

अन्वस्त : हा शांकव-कुलातील एक वक्र होय [→ शंकुच्छेद].

वृत्तशंकूला (वर्तुळाकृती पाया असलेल्या शंकूला) त्याच्या कोणत्याही एका जनिकेस (जनक रेषेस—शिरोबिंदू आणि पाया यांमधून जाणारी रेषा) समांतर असणाऱ्या आणि त्याच्या शिरोबिंदूतून न जाणाऱ्या प्रतलाने (पातळीने) छेदले असता जो छेदवक्र तो अन्वस्त होय. प्रतलास समांतर असलेली जनिका त्यास छेदणार नाही म्हणजेच अन्वस्त अनावृत्त (उघडा) आणि अनंतगामी वक्र आहे. शांकव-कुलातील सर्व वक्रांच्या बाबतीत वक्रावरील प्रत्येक बिंदूचे एका स्थिर बिंदूपासूनचे )या बिंदूला ‘नाभी’ म्हणतात) अंतर व एका स्थिर रेषेपासूनचे (या रेषेला ‘नियतरेषा’ म्हणतात) अंतर यांचे गुणोत्तर कायम (स्थिर) असते. या गुणोत्तराला ‘विक्रेंद्रता’ म्हणतात. अन्वस्ताच्या बाबतीत विकेंद्रतेचे मूल्य १ असते म्हणजेच अन्वस्तावरील प्रत्येक बिंदू नाभी आणि नियतरेषा यांपासून सारख्याच अंतरावर असतो. या गुणधर्माचा उपयोग करून अन्वस्ताचे बैजिक समीकरण काढता येते.

संदर्भ-अक्षांची योग्य निवड केल्यास पुढे दिल्याप्रमाणे अन्वस्ताचे समीकरण प्रमाणित स्वरूपात मांडता येते.

ना हा स्थिर नाभिबिंदू व स्थिर नियतरेषा दिली असता नाम हा नियतरेषेस लंब काढा.  नाम= २क समजा.नामचा मध्यबिंदू आ हा आदिबिंदू आणि आना हा क्ष-अक्ष घ्या.य-अक्ष काढा. ना चे सहनिर्देश (स्थानदर्शक संख्या) (क,०) आणि नियतरेषेचे समीकरण क्ष+क = ०आहे (कारण नियत रेषा य-अक्षाला क इतक्या अंतरावर समांतर आहे, हे उघड आहे  [→ भूमिती, वैश्लेषिक भूमिती]. आता प (क्ष,य)हा अन्वस्तावरील कोणताही बिंदू घेतला आणि पफ हा नियतरेषेवर लंब टाकला तर नाप = पफ असले पाहिजे. म्हणजेच (क्ष-क)^२+य^२ = (क्ष+क)^२ असले पाहिजे. यावरूनअन्वस्ताचे समीकरण य^२ = ४कक्षअसेलिहिता येते. आ ला अन्वस्ताचा शिरोबिंदू आणि आना या रेषेस अन्वस्ताचा अक्ष म्हणतात. 

अन्वस्ताचे काही गुणधर्म आणि वैशिष्टये खाली दिलेली आहेत. 

(१) जर (क्ष, य) हा बिंदू अन्वस्तावर असेल, म्हणजेच य^२ = ४कक्षअसेल तर (क्ष,-य) हाही बिंदू अन्वस्तावर असलाच पाहिजे, हे उघड आहे. यावरून अनवस्त त्याच्या अक्षाभोवती सममित (प्रमाणबद्ध) आहे, हे दिसून येते.

(२) नाभीमधून जाणाऱ्या आणि अक्षाला लंब असणाऱ्या जीवेस अन्व‍स्ताचा नाभिलंब म्हणतात. नाभिलंबाची लांबी ४क असते.

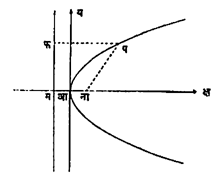(३) त या कोणत्याही सत् [→संख्या] मूल्यासाठी (कत^२, २कत) हा बिंदू य^२ = ४कक्ष या समीकरणाची पूर्तता करतो, हे उघड आहे. या बिंदूस अन्वस्तरावरील त बिंदू असे म्हणतात आणि त च्या निरनिराळ्या मूल्यांनी  अन्वस्तारावरील वेगवेगळे बिंदू दर्शवता येतात. त यास प्रचल क्ष=कत^२, य^२=२कत यांना अन्वस्तराची प्रचलीय समीकरणे म्हणतात. अशा तऱ्हेची बैजिक प्रचलीय समीकरणे असलेल्या अन्वस्त हा एकमेव शांकव होय.

(४) (क्ष_१,य_१) या बिंदूशी अन्वस्ताला स्पर्शिका (स्पर्शरेषा) काढल्यास तिचे समीकरण यय_१=२क(क्ष+क्ष_१) असते. तसेच त (प्रचल) बिंदूशी स्पर्शिका काढल्यास तिचे समीकरण यत=क्ष+कत^२ असते आणि तिचा उतार

(५) अन्वस्ताच्या कोणत्याही बिंदूशी काढलेल्या स्पर्शिकेवर नाभीपासून लंब टाकला तर त्याचा पाया यअक्षावर असतो (पहा : आकृती २).

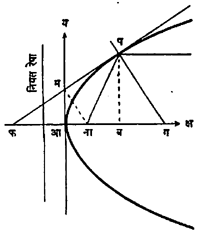(६) प (क्ष_१,य_१) बिंदूशी अन्वस्ताला प्रलंब (लंबरेषा) काढला तर त्याचे समीकरण

असते. तसेच बिंदूशी प्रलंब काढल्यास त्याचे समीकरण  

य = २ क त – त क्ष + क त^३ असे लिहता येईल. प शी काढलेला प्रलंब क्ष-अक्षास ग मध्ये छेदतो, पब क्ष-अक्षास लंब आहे आणि स्पर्शिका पब क्ष-अक्षाला फमध्ये छेदते. असे असेल तर फब आणि बग यांस अनुक्रमे अवस्पर्शिका आणि अवप्रलंब म्हणतात. फआ = आब म्हणजेच आदिबिंदू अवस्पर्शिकेचा मध्यबिंदू आहे असे दाखविता येते. तसेच अवप्रलंबाची लांबी २ कअसते म्हणजेच प च्या स्थानावर अवलंबून नसते व हे अन्वस्ताचे वैशिष्टय समजले जाते (आकृती ३).

(८) कोणत्याही बिंदूपासून अन्वस्ताला तीन प्रलंबरेषा काढता येतात. या रेषा अन्वस्ताला ज्या बिंदूशी प्रलंब असतील त्या बिंदूंच्या य-सह–निर्देशकांची बेरीज शून्य असते.

(९) नाभीमधून काढलेल्या जीवेच्या टोकांशी काढलेल्या स्पर्शिका परस्परांशी लंब असतात व त्यांचा छेदबिंदू नियतरेषेवर ध्रुवबिंदू असते आणि नियतरेषा ही नाभीची ध्रुवरेषा असते [→ शंकुच्छेद].

प हा अन्वस्तावरील कोणताही बिंदू आहे. पज या अक्षाला समांतर असणाऱ्या रेषेला अन्वस्ताचा व्यास आणि नाप हिला नाभित्रिज्या म्हणतात प शी काढलेली स्पर्शिका व प्रलंब हे नाभित्रिज्या आणि व्यास यांमधील कोनाचे दुभाजक असतात. ह्या गुणधर्मावरून असे दाखविता येईल की, जर अन्वस्ताच्या आकाराचा एखादा परावर्तक घेऊन त्याच्या नाभीच्या ठिकाणी एखादा दिवा ठेवला तर नाभीपासून निघाणारे प्रकाश-किरण क्ष-अक्षाला समांतर दिशेने परावर्तित होतील आणि ते कमाल अंतरावर जातील. दूरवर प्रकाशझोत टाकण्यासाठी (उदा., मोटारीचे दिवे) या तत्त्वाचाच उपयोग करतात.

आगाशे, क. म.

“