अंतर्वेशन व बहिर्वेशन :जर क्ष आणि य या दोन चलांमधील (बदलत्या राशींमधील) य = फ (क्ष) हा फलनसंबंध (परस्पर संबंधदर्शक समीकरण) माहीत असेल तर क्ष च्या फलन-प्रांतातील कोणत्याही मूल्यासाठी य चे मूल्य काढता येते. परंतु प्रत्यक्ष व्यवहारात दोन चलांमधील फलनसंबंध नेहमीच माहीत असतो असे नाही किंबहुना अशा तऱ्हेने संबंध अस्तित्वात आहे की काय, आणि असल्यास तो कोणत्या प्रकारचा आहे हे ठरविणे हेच उद्दिष्ट प्रामुख्याने असते. जर क्ष च्या काही मूल्यांकरिताच य ची संगतमूल्ये माहीत असतील किंवा प्रयोगाने मिळाली असतील तर त्यांवरून फलनसंबंध निश्चित स्वरूपात लिहिता येईलच असे नाही. अर्थात क्ष च्या इतर मूल्यांकरिता य ची संगतमूल्ये काय असावीत याचा अंदाज करावा लागतो. यासाठी अंतर्वेशनाचा वा बहिर्वेशनाचा उपयोग होतो.
समजा, क्ष च्या क्ष, , क्ष२ , . . . , क्षप अशा चढत्या मूल्यांसाठी य ची संगतमूल्ये अनुक्रमे य, , य२ , . . ., यप अशी आहेत. यावरून [क्ष१ , क्षप] या अंतरालातील कोणत्याही अधल्या-मधल्या मूल्यासाठी य चे संगतमूल्य काय असावे, याचा जास्तीत जास्त बरोबर अंदाज करणे म्हणेच अंतर्वेशन होय. तसेच [क्ष१ , क्षप] या अंतरालाबाहेरील क्ष-मूल्यांसाठी संगत य-मूल्ये शोधणे म्हणजे बहिर्वेशन होय. {य१ , . . ., यप }यामधील कोणत्याही य-मूल्यासाठी क्ष चे मूल्य ठरविणे म्हणजे व्यस्त-अंतर्वेशन आणि {य१ , . . ., यप } याच्या व्याप्तीबाहेरील य-मूल्यासाठी क्ष-मूल्य शोधणे म्हणजे व्यस्त-बहिर्वेशन होय.
उदा., एका देशाच्या शिरगणतीवरून पुढे दिल्याप्रमाणे कोष्टक मिळाले :
| वर्ष (क्ष) | १९०१ | १९११ | १९२१ | १९३१ | १९४१ |
| लोकसंख्या (य) कोटींमध्ये) | २३·६२ | २३·५१ | २५·१४ | २७·९० | ३१·८७ |
या कोष्टकावरून ‘१९२६ सारख्या मधल्याच एखाद्या वर्षी लोकसंख्या किती असेल? ’या प्रश्नाचे उत्तर अंतर्वेशनाने मिळेल. तसेच ‘१९४४ या वर्षी लोकसंख्या किती असेल?’ याचे उत्तर बहिर्वेशनाच्या साहाय्याने मिळेल. तसेच, २४ कोटी किंवा ३५ कोटी लोकसंख्या कोणत्या वर्षी असेल, याचे उत्तर अनुक्रमे व्यस्त-अंतर्वेशनावरून आणि व्यस्त-बहिर्वेशनावरून मिळेल.
आर्थिक व सामाजिक क्षेत्रांत अंतर्वेशन आणि बहिर्वेशन-गणित उपयुक्त ठरले आहे. वार्षिक अंदाजपत्रके तयार करणे, आयातनिर्यातीचे अंदाज वर्तवून धोरण ठरविणे, पंचवार्षिक योजनांचे आराखडे करणे इ. विषयांत संख्यात्मक निश्चित अनुमान बसविणे आवश्यक असते आणि यांकरिता अंतर्वेशन व बहिर्वेशन यांची मदत होते.
पूर्वी अंतर्वेशन हे ⇨संख्यात्मक विश्लेषणात अंतर्भूत करण्यात येत असे. आधुनिक संगणक त्यावेळी अस्तित्वात नसल्याने सर्व आकडेमोड हातानेच करावी लागत असे. तसेच हल्ली उपलब्ध असलेल्या लॉगरिथम, त्रिकोणमितीय इत्यादींसारखी सूक्ष्म कोष्टके त्या वेळी नव्हती. त्यामुळे आधिक कार्यक्षम अंतर्वेशन-सूत्रांना महत्त्व येऊन त्याचा विकास झाला. आधुनिक संगणकांमुळे या सूत्रांचा अंतर्वेशन-क्रियेसाठी फारसा उपयोग होत नसला तरी संख्यात्मक अवकलन-व समाकलन-गणितात त्यांचा उपयोग होतो, त्यामुळे हल्ली दृष्टिकोन बदललेला असला तरी या सूत्रांचे महत्व कमी झालेले नाही. अंतर्वेशन वा बहिर्वेशन या गणित क्रियेचे दोन मुख्य प्रकार म्हणजे आलेख -पद्धती आणि बैजिक पद्धती हे होत.
(१) आलेख-पद्धती : ही पद्धती वापरण्यास सोपी असली तरी त्यापासून काढलेले निष्कर्ष बरेचसे ढोबळ असतात. जर क्ष१ , क्ष२, . . .,क्षप या क्ष-मूल्यांसाठी य ची संगतमूल्ये य१, य२, . . .,यप अशी असतील तर संदर्भ अक्ष-प्रतलावर (क्ष१ , य१), (क्ष२, य२),
. . .,(क्षपयप) अशा सहनिर्देशकांच्या प बिंदूची स्थापना करतात. या सर्व पबिंदूमधून जाणारा वक्र काढल्यास तो पाहिजे असलेल्या क्ष, य मधील फलनसंबंधाचे भूमितीय प्रातिनिधिक स्वरूप असेल आणि हा आलेख वाचून पाहिजे त्या क्ष-मूल्यासाठी य-मूल्य आणि पाहिजे त्या य-मूल्यासाठी योग्य असे क्ष-मूल्य ठरवता येईल.
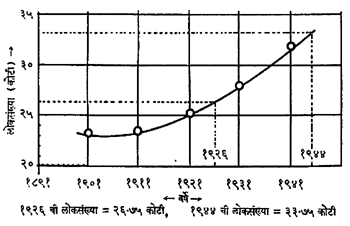
वर्ष आणि लोकसंख्या यांचे संबंध दर्शविणारा आलेख
वर दिलेल्या लोकसंख्येच्या आकडेवारीचा आलेख आकृतीत दाखविलेला आहे.
असा वक्र काढण्यामध्ये पुढील अडचणी ऊद्भवतात : वर स्थापन केलेल्या प बिंदूंमधून जाणारे अनेक वक्र काढणे शक्य आहे. त्यांपैकी कोणता निवडावा, हा प्रश्न उपस्थित होतो. तसेच एखाद्या प्रयोगातील निरीक्षणांनुसार जर य१ , य२ , . . ., यप अशी मूल्ये मिळाली असतील तर त्यांमध्ये काही प्रयोगोद्भव त्रुटी असण्याचाही संभव असतो. हे सर्व लक्षात घेऊन वरील प बिंदूंतून जाणारा किंवा त्यांच्या जास्तीत जास्त जवळून जाणारा असा मुक्तहस्त संतत वक्र काढतात. अर्थात हे करण्याला अनुभवाची व कौशल्याची जरूरी असून यात व्यक्तिगत निर्णयाचाही प्रभाव पुष्कळ असतो. एकदा असा वक्र काढला, की इष्ट ती मूल्ये आलेख वाचून काढता येतात व अंतर्वेशन इ. क्रिया साधता येतात.
(२) बैजिक पद्धती :या पद्धतीत वक्र अन्वायोजन आणि अंतर्वेशन-सूत्रे असे दोन भाग पाडता येतील.
(अ) वक्र अन्वायोजन :वर वर्णन केलेल्या आलेख-पद्धतीचे हे बैजिक रूप आहे, असे म्हणावयास हरकत नाही. पण या पद्धतीत वक्राची योग्य निवड करण्यासाठी बैजिक कसोट्या उपलब्ध असल्याने अधिक काटेकोर निष्कर्ष मिळतात. या पद्धतीत वक्राचे बैजिक समीकरण य = फ (क्ष) म्हणजेच क्ष आणि य मधील फलनसंबंध ठरविण्याचा विचार होतो. हे फलन बहुपदीच्या स्वरूपात घेण्याची प्रथा आहे. जर वक्राचे समीकरण य = क० +क१ क्ष +क२ क्ष२+ . . . + कप-१ क्षप-१असे मानले, तर क० , क१ , . . . , कप-१ हे सहगुणक असे असले पाहिजेत, की (क्ष, , य,), …, (क्षप यप) हे दिलेले प बिंदू या समीकरणाची पूर्तता करतील. म्हणजे मग यर =क० +क१ क्षर + क२ क्षर२ + … + कप-.१ क्षरप-१, र = १, २, …, प. ही प समीकरणे सोडवून क०,क,,…,कप-१ या प सहगुणकांची इष्ट मूल्ये काढता येतील. ही मूल्ये घालून वक्राचे समीकरण मांडता येईल व त्यायोगे क्ष च्या कोणत्याही मुल्याकरिता य चे संगतमूल्य काढता येऊन अंतर्वेशन वा बहिर्वेशन साधता येईल. प्रत्यक्ष व्यवहारात मात्र प हा जर मोठा पूर्णांक असेल तर असे (प-१) घाती बहुपदी समीकरण वापरणे कष्टदायक ठरते. कारण सहगुणकांची मूल्ये ठरविण्यासाठी तितकी युगपत् समीकरणे सोडवावी लागतात. याकरिता जितक्या कमी घाताची बहुपदी घेता येईल तितके चांगले. बहुधा तीनापेक्षा जास्त घाताची बहुपदी घेत नाहीत. मात्र असा वक्र सर्व प बिंदूमधून जाईलच असे नाही. ही त्रुटी कमीत कमी असावी याकरिता लघुतम वर्गपद्धतीचा उपयोग करतात. ही पद्धती पुढीलप्रमाणे आहेः समजा, य = फ (क्ष) = क० +क१ क्ष +क२ क्ष२ हे समीकरण असलेल्या वक्राचे अन्वायोजन करावयाचे आहे. क्ष = क्ष, असता य चे दिलेले मूल्य य, असून या समीकरणानुसार अपेक्षित मूल्य फ (क्ष,) असे येईल अशाच प्रकारे इतर मूल्यासंबंधी म्हणता येईल. आता स =[ य१ – फ (क्ष१)]२+[य२ – फ (क्ष२)]२ + . . . +[यप – फ (क्षप)]२असेल तर क० , क१ , क२ हे सहगुणक असे पाहिजेत, की स लहुतम असेल. कलनशास्त्रानुसार स हे क० , क१ , क२ यांचे फलन असल्यामुळे, स लघुतम असेल, तर स चे क० , क१ , क२ यांच्या सापेक्ष आंशिक अवकलज शून्य असले पाहिजेत आणि असले पाहिजेत. म्हणजेच ∂स/∂क० = ०, ∂स/∂क१ = ० आणि ∂स/∂क२ = ० असले पाहिजे. ही तीन समीकरणे सोडवून क० , क१, क२ या सहगुणकांची इष्ट मूल्ये मिळतील. अर्थातच यावरुन वक्राचे समीकरण मांडून अंतर्वेशन साधता येईल. हीच रीत वापरून अन्य घाती बहुपदी फलन घेऊन सहगुणक काढता येतात.
(आ) अंतर्वेशन-सूत्र-पद्धती :ही अधिक महत्वाची बहुपदी अंतर्वेशन-पद्धती आहे. यातील अंतर्वेशन-सूत्रांचा विचार करण्यापूर्वी सांत अंतरे व त्यांचे गुणधर्म यांची माहिती असणे आवश्यक आहे [→ सांत अंतर-कलन ] विवेचनाच्या सोयीकरता येथे त्यांचा सूत्रमय उल्लेख आवश्यक आहे. (क्षर, यक्ष र), र = ०, १, २, …,प अशा मूल्यांचे कोष्टक दिलेले असल्यास, क्ष मधील Δ क्ष या बदलाकरिता य मधील Δ यक्ष हा बदल देणारे समीकरणΔ यक्ष =यक्ष+Δ क्ष –यक्ष, हे होय. याचप्रमाणेΔ २यक्ष=Δ (Δ य क्ष) =Δयक्ष+Δक्षΔ –यक्ष असे लिहिता येईल. याच प्रकारे ∆३यक्ष, ∆४यक्ष, … ∆पयक्ष, यांच्या व्याख्या मांडता येईल. Δ ³यक्षΔ २यक्ष , Δ ३यक्ष अनुक्रमे प्रथम, द्वितीय, तृतीय, …, प कोटीची अंतरे म्हणतात. या अंतरांचा महत्वाचा गुणधर्म असा, की जर य=क०+ क१क्ष + … + कप क्षपअसा प-घाती बहुपदीय फलनसंबंध घेतल्यास Δपयक्ष= स्थिरांक आणि Δ प+,यक्ष= ० असे येते.
वरील समीकरणात Δ क्ष =ह (स्थिरांक) घेतल्यास समान अंतरे मिळतात (त्यांच्यासंबंधी अधिक स्पष्टीकरण खाली दिलेले आहे) व त्यावरुंन अग्रगामी, प्रतिगामी आणि मध्य अंतर-सूत्रे मांडता येतात. अग्रगामी, प्रतिगामी व मध्य अंतरांच्या व्याख्या पुढील कोष्टकावरुन स्पष्ट होतील. ही अंतरे दर्शविण्यासाठी अनुक्रमे
Δ, ∇ आणि इ ही चिन्हे वापरली आहेत.

या अंतराची अन्योन्य संबंध दर्शविणारी सूत्रे संदर्भाकरिता खाली दिलेली आहेत.

अंतर्वेशन-सूत्रे (समान अंतरे) : समजा, क्ष०, क्ष१, …, क्षप ही क्ष ची मूल्ये समान अंतरांवर आहेत आणि कोणत्याही दोन लगतच्या क्ष मूल्यांमधील अंतर ह आहे (क्षर+१-क्षर = ह) या क्ष मूल्यांशी संगत अशी य मूल्ये य०, य१,…, यप दिलेली आहेत. आपल्याला क्ष० आणि क्ष१, यांमधील एखाद्या क्ष-मूल्यासाठी य शोधावयाचा आहे. म्हणजेच क्ष = क्ष० + अह, ० < अ < १असता य चे मूल्य काढावयाचे आहे. आता अग्रगामी पद्धतीने य१ –य० या फरकास Δ य०, य२ -य१याला Δ य१…असे म्हणतात. तसेचΔ २य० =Δ य१ – Δ य०,Δ २य१ =Δ य२ – Δ य१,…. इ.द्वीतीयांतरे लिहता येतील अशा तऱ्हेने Δ य०,Δ २य,Δ ३य०, … ही निरनिराळ्या कोटींची अंतरे लिहिता येतील. ही अंतरे वापरून पुढे दिलेल्या सूत्रानुसार क्ष = क्ष० + अह असता य चे यक्ष+अह हे मुल्य इष्ट मिळवता येते.
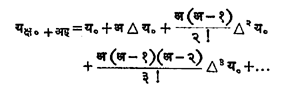
हे सूत्र ‘ग्रेगरी-न्यूटन यांचे अग्रगामी अंतर्वेशन-सूत्र’ म्हणून ओळखले जाते.
जर क्ष, य मधील फलनसंबंध प-घाती बहुपदीने दर्शविण्यायोग्य असेल तर Δ पय० स्थिरांक व Δ प+१य० शून्य असेल. म्हणजेच वरील सूत्रामध्ये पहिल्या प+१ पदानंतरची पदे लक्षात घेण्याचे कारण नाही. खालील उदाहरणावरून हे विवरण स्पष्ट होईल:
| क्ष | य | Δ | Δ२ | Δ३ |
| ० | १⋅००३ | |||
| ७⋅९९९ | ||||
| १ | ९⋅००२ | १०⋅००२ | ||
| १८⋅००१ | ०,००२ | |||
| २ | २७.००३ | १०.००० | ||
| २८⋅००१ | ०⋅००० | |||
| ३ | ५५⋅००४ | १०⋅००० | ||
| ३८⋅००१ | ||||
| ४ | ९३⋅००५ |
या कोष्टकातील Δ ३ यक्ष जवळजवळ शून्य म्हणजेच उपेक्षणीय आहेत. समजा, आपणाला य ०.५ हे मूल्य हवे आहे वरील सूत्रानुसार
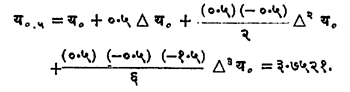
वरील मूल्ये य = १ + ३ क्ष + ५ क्ष२या बहुपदीशी सन्निकट आहेत, हे पडताळून पाहता येईल. अंतर्वेशन-सूत्राने मिळालेले मूल्य ३.७५ या यथार्थ मूल्याशी जुळते आहे. आवश्यक तर य = १ + ३ क्ष + ५ क्ष२या अन्वस्ताचा आलेख काढूनही पडताळा पहाता येईल.
ग्रेगरी-न्यूटन यांच्या अंतर्वेशन-सूत्रात अग्रगामी अंतरे वापरलेली असल्यामुळे ते कोष्टकाच्या प्रारंभीच्या मधल्या मूल्यांकरिता अंतर्वेशन करण्यासाठी उपयुक्त ठरते.
ग्रेगरी-न्यूटन यांच्या दुसऱ्या सूत्रात कोष्टकाच्या शेवटच्या मूल्यांपासून मागे मागे जाणाऱ्या म्हणजे प्रतिगामी अंतरांचा उपयोग करतात. अग्रगामी सूत्राप्रमाणेच क्ष = क्षप – अह घेऊन हे सूत्र खालीलप्रमाणे मांडता येते :

कोष्टकातील शेवटच्या नोंदीमधील अंतर्वेशन वा बहिर्वेशन करण्याकरिता या सूत्राचा उपयोग करतात.
सरल अंतर्वेशन (असमान अंतरे) : क्ष या स्वयंचलाची मूल्ये परस्परांपासून असमान अंतरावर असल्यास अंतर्वेशन करण्याकरिता विभाजिन अंतरे वापरावी लागतात. (क्षर , यर), र = ०, १,…, प हा फलनसंबंध दिलेला असल्यास प्रथम, द्वितीय इ. कोटीच्या विभाजित अंतरांची व्याख्या खालीलप्रमाणे करतात :
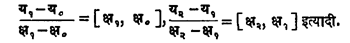
यांना ‘प्रथम कोटीची विभाजित अंतर’ म्हणतात.

यातील शेवटचे पद सूत्राची त्रुटी दर्शविते. न्यूटन यांच्या सूत्राचा उपयोग खालील उदाहरणावरूण स्पष्ट होईल

य = फ (क्ष) हे फलन प-घाती असेल तर प+१ कोटीचे सांत अंतर शून्य असले पाहिजे म्हणून न्यूटन यांच्या सूत्रात[क्ष, क्ष०,…,क्षप] = ० घेऊन ते सूत्र पुढीलप्रमाणे लिहिता येईल :

या सूत्राला ‘लाग्रांज यांचे अंतर्वेशन-सूत्र’ म्हणातत. या सूत्रात कोणत्याही अंतर-सूत्राचा अवलंब केलेला नाही.

या सूत्रावरून (१) स्वयंचलांची दिलेली मूल्ये समानांतरित नसतील तेव्हा उपलब्ध असलेल्या स्वयंचलांची संगतमूल्ये ठरविता येतात आणि (२) फलनाची कोष्टकात नसलेली मूल्ये घेतल्यास त्यावरून स्वयंचलाची संगतमूल्ये काढता येतात. याच कृतीला ‘व्यस्त अंतवशन’ म्हणतात.
मध्य अंतर अंतर्वेशन-सूत्रे : विभाजित अंतरे व साधी अंतरे यांची तुलना व परस्परसंबंध दर्शविणारे सूत्र म्हणजे
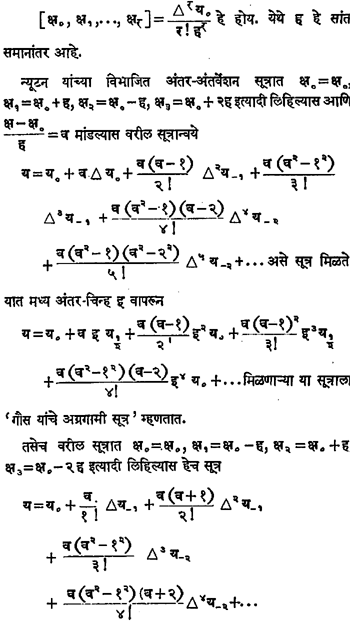
असे मिळते व त्यात मध्य अंतर-चिन्ह इ वापरून मिळणारे सूत्र
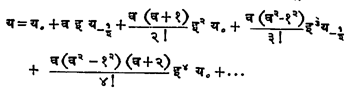
‘गौस यांचे प्रतिगामी सूत्र’ म्हणून ओळखले जाते. या सूत्रात सुरूवातीची संख्या य० न घेता य१घेतल्यास आणि पुढील अंतरे प्रतिगामी सूत्रातील अंतरांच्या समांतर रेषेतून घेतल्यास पुढील सूत्र मिळते :
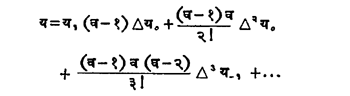
यात मध्य अंतर-चिन्ह वापरून मिळणाऱ्या सूत्राला ‘गौस यांचे तिसरे सूत्र’ म्हणतात. या तिन्ही सूत्रांत येणारी सांत अंतरे कोष्टकरूपाने खाली दिलेली असून सूत्रे अनुक्रमे ग१, ग२, ग३अशी दर्शविली आहेत.

ग१ आणि ग३ यांची सरासरी घेतल्यास येणाऱ्या सूत्रास ‘बेसेल-सूत्र’ म्हणतात.
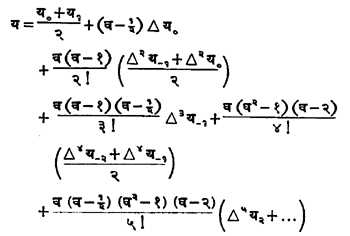
वरील कोष्टकातील क्ष० व क्ष१ समोरील सम क्रमांकांच्या अंतरांचा उपयोग करून गौस यांच्या अग्रगामी व प्रतिगामी अंतर्वेशन-सूत्रांच्या साहाय्याने महत्वाचे असे एव्हरेट-सूत्र मिळते. ते असे—
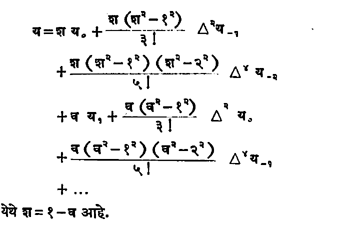
बहिर्वेशन : याकरिता अंतर्वेशन-सूत्रांचाच उपयोग करून इष्ट त्या बाहेरच्या क्ष करिता यक्ष चे मूल्य काढता येते. परंतु क्ष चे कोष्टकातील मूल्य क्ष०, क्ष१,…,क्षप या मूल्यांपासून फार दूर असल्यास सूत्राने ठरविलेले मूल्य विशेष विश्वासार्ह मानता येत नाही. यामुळे अंतर्वेशनापेक्षा बहिर्वेशन करताना अधिक काळजी घ्यावी लागते. य = फ (क्ष) हे बैजिक फलन विश्वासार्हतेच्या दृष्टीने निश्चित झालेले असल्यास अंतर्वेशन व बहिर्वेशन यांत फारसा फरक पडत नाही.
त्रुटि-सूत्रे : अंतर्वेशन-सूत्रांवरून मिळालेले य = फ (क्ष) हे क्ष ला संगत असणारे मूल्य फ (क्ष) च्या यतार्थ मूल्याचे सन्निकट-मूल्य असते. त्यामुळे प्रत्येक वेळी अशा मूल्यातील त्रुटी ठरविणे आवश्यक ठरते. वरील अंतर्वेशन-सूत्रांच्या विवेचनावरून प्रत्येक क्ष करिता
यक्ष = फ (क्ष) = ई (क्ष)+त्र (क्ष)
त्र (क्ष) = (क्ष-क्ष०)…(क्ष-क्षप) स (क्ष)
असे समीकरण मांडल्यास आणि ई (क्षर) = फ (क्षर), [ र = ०,१,२…,प ] घेतल्यास ई (क्ष) ला ‘अंतर्वेशन-फलन’ वत्र (क्ष) ला ‘त्रुटि-फलन’ म्हणतात. येथे यक्ष हे यथार्थ मूल्य होय.
अवकलनशास्त्रातील रोल-सिद्धांत प+१ वेळा वापरून
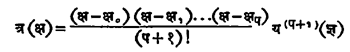
असे त्रुटि-सूत्र मिळते. येथे क्ष < ज्ञ < क्षप.
अंतर्वेशन-सूत्रांचा उपयोग : विषम कोटीच्या अंतराने शेवट होणारे स्टर्लिंग-सूत्र व सम कोटीच्या अंतराने शेवट होणारे बेसेल-सूत्र या सूत्रांखेरीज बाकीची सर्व सूत्रे कोष्टकवार मांडलेल्या चलांच्या मूल्यांच्या एकाच गटाकरिता बैजिक दृष्टया समान आहेत. समान अंतरे असलेल्या चलांच्या मूल्यांकरिता हाताने आकडेमोड करण्यासाठी लाग्रांज-सूत्रापेक्षा अंतरकोष्टके सहजपणे तयार करता येत असल्यामुळे सांत अंतर्वेशन-सूत्रे अधिक सोयीची आहेत.
सर्वसाधारणपणे एखाद्या अंतर्वेशन-सूत्रातील किती पदे घेतली असता आपणास इच्छित अचूकता मिळू शकेल, हे अगोदर सांगणे शक्य नसते. त्यामुळे सामान्यतः सूत्रामधील पुढची पदे उच्च कोटीच्या अंतराचे गणित करून अशा तऱ्हेने घेतली पाहिजेत, की आपणास इष्ट तितक्या दशांश-स्थळांपर्यंत अंतर्वेशित मूल्ये स्थिर राहून अधिक समावेश केलेल्या पदांमुळे होणारा बदल क्षणीय असावा. तसेच त्रुटि-सूत्रांचा उपयोग करून ज्या सूत्रामुळे कमीत कमी त्रुटी येईल असे सूत्र निवडणे इष्ट असते. तथापि कोणते सूत्र वापरावयाचे हे ठरविणे सैद्धंतिक विचारांपेक्षा प्रत्यक्ष परिस्थितीच्या सोयीवर अवलंबून असते. व्यवहारात बहुधा बेसेल व एव्हरेट यांचीच सूत्रे वापरतात. या सूत्रांतील सहगुणकांच्या मूल्यांची कोष्टके तयार करून अंतर्वेशनाचे काम बरेचसे सुलभ करता येते.
वरील गोष्टींचा विचार करून काढलेली सर्वसाधारण अनुमाने पुढे दिलेली आहेत. ग्रेगरी-न्यूटन यांचे प्रतिगामी सूत्र कोष्टकातील शेवटची मूल्ये काढण्याकरिता उपयुक्त ठरते. कारण त्या ठिकाणी गौस-सूत्र वापरण्याइतकी पुरेशी पदे नसतात. त्याचप्रमाणे ग्रेगरी-न्यूटन यांचे अग्रगामी सूत्र मुख्यतः कोष्टकांच्या सुरूवातीच्या मूल्यांच्या अंतर्वेशनासाठी उपयोगी पडते. परंतु अंतर्वेशन करावयाच्या मूल्याच्या दोन्ही बाजूंस पुरेशी मूल्ये उपलब्ध असल्यास, ग्रेगरी-न्यूटन यांच्या दोन्ही सूत्रांपेक्षा गौस यांचे सूत्र जास्त सोयीचे असते. विशिष्ट सूत्रांच्या बाबतीत बोलावयचे झाल्यास, सम कोटीच्या अंतराने शेवट झालेले स्टर्लिंग-सूत्र व चे मूल्य शून्याच्या जवळ असल्यास उपयोगी पडते. तसेच विषम कोटीच्या अंतराने शेवट होणारे बेसेल-सूत्र व चे मूल्य १/२ च्या जवळ असल्यास उपयुक्त ठरते.
कोणत्याही अंतर्वेशन-सूत्रातील पदांची केवळ संख्या वाढवून इच्छित असलेली कितीही अचूकता मिळू शकेल, असे वाटण्याचा संभव आहे. तथापि प्रत्यक्षात कोष्टकातील मूल्ये अनंताप्रत वाढवून तयार झालेली अंतर्वेशन-श्रेढी फक्त अनंतवर्ती अभिसारी असते. म्हणजेच, आपण जसजशी मूल्यांची संख्या वाढवीत जाऊ, तसतशी त्रुटी प्रथमतः कमी होते आणि एखाद्या विशिष्ट मूल्यानंतर ती वाढावयास लागते आणि त्यानंतर ती अमर्यादपणे वाढत जाते. अर्थात अंतर्वेशनातील अचूकपणा प्रत्यक्ष व्यवहारात बहुतेक वेळा साध्य होतो. म्हणजेच अनंतवर्ती अभिसारिता सर्वसाधारण चांगली असते.
इतिहास : १६५५ च्या सुमारास वॉलिन यांनी वर्तुळाचे क्षेत्रफळ व पर्यायाने Π ची संख्यात्मक निश्चिती करण्यासाठी निर्माण केलेल्या गणितातून अंतर्वेशन-गणिताचा प्रारंभ झाला. १६७६ मध्ये न्यूटन यांनी द्विपद-प्रमेय शोधून काढल्यानंतर १६७८ मध्ये त्यांनी त्यांच्या नावाने प्रसिद्ध असलेले अंतर्वेशन-सूत्र मांडले. ऑयलर-लाग्रांज-सूत्र १७५५ मध्ये व गौस यांचे सूत्र १८१२ मध्ये प्रसिद्ध झाले. ग्रह व ताऱ्यांचे ज्योतिषविषयक संख्यात्मक गणित करणे, निरनिराळी गणितीय कोष्टके तयार करणे, यांत्रिकरीत्या समाकलन करणे यांमध्ये आकडेमोड सुलभ करण्यासाठी अंतर्वेशन-सूत्रांचा प्रामुख्याने उपयोग झाला. लाप्लास यांनी संभाव्यता-सिद्धांताचा पाया घातल्यानंतर, बेर्नुली-संख्या आणि ऑयलर-मॅक्लॉरिन-सूत्रांमुळे अंतर्वेशन व बहिर्वेशन क्रियांना मूलभूत असलेल्या, सांत अंतरकलनशास्त्रास चालना मिळाली. कोशी यांच्या वैश्लेषिक गणितावरून स्फूर्ती घेऊन अंतर्वेशन-सूत्रासंबंधीची त्रुटि-सूत्रेही १८२२ च्या सुमारास मांडली गेली. सांत अंतरकलनास याकोप बेर्नुली यांच्यापासून सुरूवात झालेली असली, तरी आधुनिक वैश्लेषिक फलनकल्पनांचा उपयोग करून प्वँकारे (१८८५) यांनी या विषयाचा आधुनिक दृष्टिकोनातून अभ्यास केला. या विषयातील आधुनिक गणितज्ञ म्हणजे बर्कॉफ (१८८४-१९४४, अमेरिका), कारमायकेल (१८७९- , अमेरिका), पिन्शेर्ले (१८५३-१९३६, इटली), नॉर्लंड (१८८५ -, स्कँडिनेव्हिया) व मिल्न टॉमसन (ब्रिटन) हे होत.
पहा : सांतअंतरकलन, विमाविषयक सांख्यिकी.
संदर्भ : 1. Freeman, H. Mathematics for Acturial Students, Part II, Cambridge, 1952.
2. Nobel, B. Numerical Methods, Vol. II. New York, 1964.
3. Scarborough, J. B. Numerical Mathematical Analysis, Oxford, 1964.
4. Steffensen J. F. Interpolation. New York, 1950.
चिखलीकर, अ. ना.