सांख्यिकीय अनुमानशास्त्र

सांख्यिकीय अनुमानशास्त्र : एखाद्या समष्टीच्या (समुदायाच्या) अज्ञात प्रचलांबद्दल अनुमान वर्तविणे हे सांख्यिकीय अनुमानशास्त्राचे मुख्य उद्दिष्ट आहे. अठराव्या शतकात आणि एकोणिसाव्या शतकाच्या आरंभी ⇨बेर्नुली, मॉवरे, थॉमस बेझ, ⇨प्येअर सीमाँ मार्की द लाप्लास, ⇨ कार्ल फ्रीड्रिख गौस  इ. गणितज्ञांनी सांख्यिकीय अनुमानशास्त्र या विषयात महत्त्वाचे संशोधन केलेले आहे. त्यानंतरच्या काळात ⇨कार्ल पीअर्सन, ⇨सर रॉनल्ड एल्मर फिशर, जेर्झी नेमन आणि अब्राहम वॉल्ड यांचे योगदान अतिशय महत्त्वाचे आहे. सांख्यिकीय अनुमानशास्त्रात अनुमाने काढण्यासाठी समष्टीमधून यदृच्छ प्रतिदर्श घेऊन त्याचे विश्लेषण केले जाते. ह्या विश्लेषणाचे प्रामुख्याने दोन भाग आहेत : (१) आकलन किंवा आगणन, (२) गृहीतक परीक्षण.  

अनुमानशास्त्रात आकलक व आकल या दोन संज्ञा येतात. प्रचलाचे अनुमान करण्यासाठी उपयोगात आणलेल्या नियमाचे सूत्र मिळविले जाते. या नियमाला आकलक म्हणतात. आकलक व संख्यानक यांच्या व्याख्या समानार्थी आहेत. एखाद्या विशिष्ट संदर्भात मिळविलेल्या आकलकाच्या मूल्याला आकल म्हणतात. उदा., प्रतिदर्शाचा माध्य हे आकलक आहे. ते कसे काढावयाचे याचा नियम ( किंवा सूत्र ) असतो. त्याचे एखाद्या उदाहरणात काढलेले २·४ मूल्य हे त्या उदाहरणाच्यासंदर्भातील आकल होते. सर्वसाधारणतः गणितज्ञ व सांख्यिकीविज्ञ हेजास्त करून आकलकाबद्दल चर्चा करतात, तर अर्थशास्त्रज्ञांनाआकलाबद्दल जास्त आस्था असते. आकलक आणि आकल यासंज्ञांधील हा फरक ‘फलन’ व त्या ‘फलनाचे मूल्य’ या दोनसंज्ञांमधील फरकासारखा आहे. f (x) = x² हे फलन असून x = 2 असतानाचे त्याचे मूल्य 4 आहे. ज्याप्रमाणेएकाच फलनाच्या x या स्वचलाची विविध मूल्ये त्या फलनाची विविध मूल्ये प्रदान करतात, त्याच प्रकारे एकच आकलक निरनिराळ्या प्रतिदर्शाच्या संबंधात निरनिराळी आकले देतो. सांख्यिकीय अनुमानशास्त्राचे मुख्य काम अज्ञात प्रचलांचे निरनिराळे गुणधर्म असणारे आकलक मिळविणे हे असते. 

 

 

आकलन व गृहीतक परीक्षण ही दोन्ही विश्लेषणे प्रचलात्मक व अप्राचलात्मक अशा दोन प्रकारे केली जातात. जेव्हा समष्टीच्या संभाव्यता फलनाचे स्वरूप माहीत नसते तेव्हा ⇨अप्राचलात्मक पद्घती   वापरल्या जातात. येथे प्रचलात्मक विश्लेषणाचे वर्णन केले आहे. तसेच बेझियन अनुमानशास्त्र व ⇨अनुक्रमात्मक विश्लेषण यांचा थोडक्यात उल्लेख केला आहे. 

प्रचलात्मक आकलन :बिंदू आकलन : ह्या पद्घतीत ज्यासमष्टीमधून प्रतिदर्श घेतलेला असतो, त्याच्या संभाव्यता घनता-फलनाचेस्वरूप f (x θ), θ ϵ Ω हे माहीत असते. परंतु θ चेमूल्य अज्ञातअसते. येथे संच Ω प्रचल θ चे अवकाश दर्शविते. यदृच्छ प्रतिदर्शाच्या आधारे जेव्हा प्रचल θ  चेविशिष्ट मूल्य निश्चित केले जातेतेव्हा त्या पद्घतीस बिंदू आकलन असे म्हणतात. जर   X₁, X₂, …. , X_n हा f ( x θ) ह्या  संभाव्यता घनता-फलनातून घेतलेला n ह्या आकारविस्ताराचा यदृच्छ प्रतिदर्श असेल तर T ( X₁, X₂, …. , X_n ) हे X₁, X₂, …. , X_n चे असे फलन शोधून काढावयाचे असते की जे अज्ञात प्रचलθ संबंधीउपयुक्त अंदाज वर्तवू शकेल.T ( X₁, X₂, …. , X_n ) ह्यास θ चाआकलक असे म्हणतात तोखालीलप्रमाणे लिहिला जातो. 

                

जर  X₁, X₂, …. , X_n  ही प्रतिदर्शाची निरीक्षित मूल्ये असतील तर T ( X₁, X₂, …. , X_n ) या आकलकाचे

 t ( X₁, X₂, …. , X_n ) हे निरीक्षित मूल्य असते आणि त्यास प्रचलθ  चाआकल असे म्हणतात. 

आकलक T ( X₁, X₂, …. , X_n ) याचे मूल्यमापन करण्यासाठीअनेक निकष उपलब्ध आहेत : (१) निरभिनता, (२) सुसंगतता, (३)कार्यक्षमता व (४) पर्याप्तता. 

निरभिनता : जर T ( X₁, X₂, …. , X_n ) ह्या आकलकाचे अपेक्षितमूल्य E (T) =θअसेलतर त्यास निरभिनत आकलक असे म्हणतात.हा जरी इष्ट गुणधर्म असला तरी काही आकलक निरभिनत नसतात. 

उदा., (१) समष्टीचा माध्य ( μ) अस्तित्वात असेल तर प्रतिदर्शाचामाध्य (x) हा नेहमीच μ चानिरभिनत आकलक असतो. (२) प्रतिदर्शाचा मध्यक हा सर्वसाधारणतः समष्टीच्या मध्यकाचा निरभिनतआकलक नसतो. (३) प्रतिदर्शाचा विचरण हा कधीच समष्टीच्या विचरणाचा निरभिनत आकलक नसतो. (४) n आकारविस्तार असलेल्या प्रतिदर्शाचा विचरण S² असल्यास हा समष्टीच्या विचरणाचा निरभिनत आकलक  असतो. 

गुणधर्म : सर्वसाधारणतः समष्टीच्या एकाच प्रचलाचे अनेक निरभिनत आकलक असू शकतात. जर θयाप्रचलाचे T₁ व T₂ हे दोन भिन्न निरभिनत आकलक असतील, तर l₁T₁ + l₂ T₂ ( जेथे l₁ + l₂ = 1) हा देखील θचानिरभिनत आकलक असतो. 

सुसंगतता : जर T_n (X_१, X_२, …. , X_n) हा n ह्या आकारविस्ताराच्या प्रतिदर्शावर आधारित θ चाआकलक असेल आणिप्रतिदर्शाचा आकारविस्तार वाढवीत नेल्यास (n Ž→¥), जर T_n आणिθमधीलकेवल अंतर शून्यवत होत असेल, तर T_n ह्यास सुसंगतआकलक असे म्हणतात. सुसंगत आकलकाची व्याख्या खालीलप्रमाणेमांडता येते. जर तर T_n ह्यास θ चा सुसंगत आकलक असे म्हणतात. 

उदा., (१) प्रतिदर्शाचा माध्य हा सांत विचरण असणाऱ्या समष्टीच्यामाध्याचा सुसंगत आकलक असतो. (२) विचरण माहीत असलेल्याप्रसामान्य समष्टीच्या माध्य या प्रचलाचे, प्रतिदर्शाचे माध्य व मध्यक हेदोन्ही सुसंगत आकलक आहेत. (त्यातील माध्य हा सर्वांत जास्तकार्यक्षम आकलक आहे). 

गुणधर्म : सर्वसाधारणतः मोठा आकारविस्तार असलेल्या प्रतिदर्शापासूनएकाच प्रचलाचे अनेक सुसंगत आकलक मिळतात. 

कार्यक्षमता : कार्यक्षमता विचरणाच्या व्यस्त प्रमाणात असते. ज्याआकलकाचे विचरण कमी असते त्याची कार्यक्षमता जास्त असते.T_१ व T_२ हे θ  याप्रचलाचे दोन भिन्न निरभिनत आकलक असतीलआणि (T_१ चे विचरण) &lt (T_२ चे विचरण ), तर T_१ हा आकलकT_२ या आकलकापेक्षा अधिक कार्यक्षम आहे असे म्हणतात.(T_१ चे विचरण) /(T_२चे विचरण) या गुणोत्तराला T_२ ची T_१ च्यासंबंधातील (तुलनेतील) कार्यक्षमता म्हणतात. ज्या T (X_१, X_२, …. ,X_n) या निरभिनत आकलकाचे विचरण क्रामर-राव असमानतेच्यानिम्नबंधाएवढे असते, त्यास सर्वांत जास्त कार्यक्षम आकलक म्हणतात. 

गुणधर्म : (१) सर्वसाधारणतः सर्वांत जास्त कार्यक्षम आकलक हेमोठा आकारविस्तार असलेल्या प्रतिदर्शापासून मिळू शकतात. (२)एखाद्या प्रचलाचा सर्वांत जास्त कार्यक्षम आकलक अस्तित्वात असेलतर तो अनन्य असतो. 

---

जर T हा सर्वांत जास्त कार्यक्षम आकलक असेल तर T’ यादुसऱ्यानिरभिनत आकलकाची T च्या संबंधातील कार्यक्षमता, E (T ‘) =      या गुणोत्तराने दाखविली जाते. साहजिकच0≤ E (T´) ≤1. अशा तऱ्हेने केलेल्या कार्यक्षमतेच्या मापनामुळे विविध आकलकांची त्यांच्या कार्यक्षमतेबाबतीत तुलना करता येते. जर सर्वांत जास्त कार्यक्षम आकलक अस्तित्वातच नसेल तर इतर आकलकांच्या कार्यक्षमतांची अशा तऱ्हेने तुलना करता येत नाही. 

पर्याप्तता : पर्याप्त संख्यानकाची संकल्पना फिशर यांनी प्रथम मांडली. नंतर नेमन यांनी पर्याप्त संख्यानक शोधण्यासाठी एक साधा निकषसांगितला जो ‘नेमन-फिशर घटकात्मक सिद्घांत’ म्हणून प्रसिद्घ आहे.पर्याप्त संख्यानकात प्रचल θ संबंधीप्रतिदर्शात उपलब्ध असलेली सर्वमाहिती साठविलेली असते. म्हणून प्रचल θ साठीपर्याप्त संख्यानकउपलब्ध असेल तर त्यावर आधारित आकलकाद्वारे θ  साठीअंदाजवर्तविला जातो. 

पर्याप्त आकलकाची सम्यक् व्याख्या शक्यता फलनाच्या संकल्पनेवरअवलंबून आहे. ही शक्यता फलनाची संकल्पना पुढे पाहिली जाईल. 

उदा., (१) प्रतिदर्श माध्य हा e^–m.m^r/r! (r = 0, 1, 2, … ) हे संभाव्यता फलन असलेल्या प्वासाँ समष्टीच्या m या प्रचलाचा पर्याप्त आकलक आहे. (२)हे संभाव्यता घनता-फलन असलेल्या कोशी या संतत वंटनाच्या θया प्रचलासाठी पर्याप्त आकलक उपलब्ध नाही. 

गुणधर्म : θयाप्रचलाचा T₁ हा पर्याप्त आकलक असेल व T₂ हा दुसरा एखादा आकलक असेल तर, T₁ दिला असताना T₂ चे सशर्त प्रतिदर्शी वंटन हे θ-मुक्त असते (θवरनिरवलंबी असते ).

काही संदर्भात, मोठ्या आकारविस्ताराचा प्रतिदर्श वापरून केलेले आकलन व कोणत्याही (पण मुख्यतः लहान) आकारविस्ताराचा प्रतिदर्श वापरून केलेले आकलन हे वेगवेगळे अभ्यासिले जाते. मोठ्या आकार-विस्ताराच्या प्रतिदर्शांच्या अभ्यासातून मिळणारी इच्छाफले ही अधिक सरल व सोपी असतात. त्यामुळे कोणत्याही आकारविस्ताराच्या प्रतिदर्शांच्या अभ्यासातून मिळालेली इच्छाफले वापरण्याऐवजी मोठ्या आकार-विस्ताराच्या प्रतिदर्शांच्या अभ्यासातून मिळालेली इच्छाफले त्यांच्या संदर्भात वापरणे सुलभ होते.

सर्वसाधारणतः लहान आकारविस्तारांच्या प्रतिदर्शाच्या अभ्यासातून मिळालेल्या आकलकांच्या बाबतीत निरभिनता हा गुणधर्म आवश्यक व कार्यक्षमता (आणि जमल्यास सर्वांत जास्त कार्यक्षमता–जरी हा गुणधर्म लहान प्रतिदर्शांच्या बाबतीत कमी वेळा आढळतो –) हा गुणधर्म इष्ट मानला जातो. याउलट मोठ्या आकारविस्तारांच्या प्रतिदर्शांच्या अभ्यासातून मिळालेल्या आकलकांच्या बाबतीत सुसंगतता हा गुणधर्म आवश्यक व कार्यक्षमता (आणि जमल्यास सर्वांत जास्त कार्यक्षमता – जो सर्वसाधारणतः या बाबतीत आकलकातून आढळून येतो –) हा गुणधर्म इष्ट मानतात. 

बिंदू आकलने काढण्याच्या अनेक पद्घती आहेत : (१) महत्तम शक्यता पद्घती, (२) परिबल पद्घती, (३) लघुतम-वर्ग पद्घती व (४) लघुतम काय-वर्ग पद्घती. 

महत्तम शक्यता पद्घती   :  ही पद्घत फिशर यांनी शोधून काढली. ही सर्वांत जास्त प्रचलित पद्घत आहे. जर  X_१, X_२, … , X_n हा f (x θ) ह्या संभाव्यता घनता -फलनातून घेतलेला यदृच्छ प्रतिदर्श असेल तर X_१, X_२, …. , X_n चे संयुक्त संभाव्यता घनता-फलन f ( x₁ θ).f ( x₂ θ) …. f ( x_n θ) असे असते. हे संयुक्त संभाव्यता घनता-फलन θ चेफलन आहे असे समजल्यास त्यास शक्यता फलनअसे संबोधतात. ते खालीलप्रमाणे मांडता येते. 

L (θ x₁, x₂, …. , x_n) =f (x₁ θ) . f (x₂ θ) . …. . f (x_n θ)जर x₁, x₂, …. , x_n ह्या निरीक्षित प्रतिदर्शाचे t (x₁, x₂, …. , x_n) हे, असे फलन शोधून काढले की, जे θ च्याऐवजी शक्यता फलनातवापरल्यास, शक्यता फलन L महत्तम मूल्य गाठते, तर T (X₁, X₂,…. , X_n ) ह्या संख्यानकास θ चेमहत्तम शक्यता पद्घतीने काढलेलेआकलक असे म्हणतात आणि ते खालीलप्रमाणे लिहिले जाते. 

सर्वसाधारणपणे ही आकलने हे समीकरण सोडवून काढता येतात. संभाव्यता घनता-फलन θ₁, θ₂, … , θ_rह्या r  

अज्ञात प्रचलांवर अवलंबून असेल तर खालील समीकरणे सोडवून 

θ₁, θ₂, … , θ_rची महत्तम शक्यता पद्घतीने काढलेली आकलके मिळतात. ह्या पद्घतीने काढलेली आकलके सुसंगत व कार्यक्षम असतात. ही आकलके निरभिनत असतातच असे नाही. उदा., X₁, X₂,… , X_n हा N ( θ,σ² ) ह्या प्रसामान्य घनता-फलनातून घेतलेला प्रतिदर्श असेल, तर θ ह्याप्रचलाचे महत्तम शक्यता पद्घतीने काढलेले आकलक

हे असते आणि ते निरभित असते परंतु σ² ह्या प्रचलाचे महत्तम शक्यता पद्धतीने काढलेले आकलन हे निरभिनत नसते.

ह्या पद्घतीचा आणखी एक गुणविशेष म्हणजे जर का प्रचल θ साठी पर्याप्त संख्यानक उपलब्ध असेल तर महत्तम शक्यता पद्घतीने काढलेली 

आकलके ही पर्याप्त संख्यानकाची फलने असतात. 

परिबल पद्घती : एखाद्या समष्टीचे संभाव्यता घनता-फलनf (x θ₁, θ₂, … , θ_r ) हे जर θ₁, θ₂, … , θ_rह्या r अज्ञात प्रचलांवरअवलंबून असेल तर X₁, X₂,… , X_n ह्या प्रतिदर्शाच्या आधारे प्रथमr परिबलांची मूल्ये खालील सूत्राने काढली जातात. 

समष्टीची परिबले E [ X^k ] , जी θ₁, θ₂, … , θ_rह्या प्रचलांची फलने असतात, ती प्रतिदर्शाच्या परिबलांशी समान आहेत असे समजून r समीकरणे मांडता येतात. ही समीकरणे सोडवून θ₁, θ₂, … , θ_rह्या प्रचलांची आकलने मिळविली जातात. ह्या पद्घतीने मिळालेली आकलके 

सुसंगत असतात. 

लघुतम-वर्ग पद्घती : ह्या पद्घतीत प्रामुख्याने 

ही वर्गांची बेरीज विचारात घेतली जाते. येथे y_i ह्या निरीक्षणाचे अपेक्षित मूल्य E (y_i) हे θ₁, θ₂, … , θ_rह्या r अज्ञात प्रचलांवर अवलंबून असते. ह्या प्रचलांची आकलके खालील समीकरणे सोडवून मिळविली जातात. 

ही पद्घत प्रामुख्याने समाश्रयण विश्लेषणात वापरली जाते. ही पद्घत गौस ह्यांनी १८२१ साली रेषीय प्रतिमानांचे विश्लेषण करण्यासाठी प्रचारात आणली. ह्या पद्घतीद्वारे काढलेली आकलके निरभिनत असून त्यांचे विचरण लघुतम असते. 

---

लघुतम काय-वर्ग पद्घती : ही पद्घत कार्ल पीअर्सन यांनी शोधून काढली. ही पद्घत पृथक् गटनिहाय किंवा संतत संभाव्यता घनता-फलनाच्या अज्ञात प्रचल θ चेआकलन काढण्यासाठी वापरतात. जेव्हाn निरीक्षणे k गटांत विभागलेली असतात तेव्हा ह्या पद्घतीचा वापर केलाजातो. जर n₁, n₂, … , n_k ह्या k गटांच्या निरीक्षित वारंवारता असतील आणि p₁(θ), p₂ (θ), … , p_k (θ) ह्या k गटांच्या संभाव्यता असतील तर निरीक्षित वारंवारता आणि अपेक्षित वारंवारता यांधील फरक खालील काय-वर्ग संख्यानकाद्वारे मोजला जातो. 

अज्ञात प्रचल θ चे लघुतम काय-वर्ग पद्धतीने आकलक मिळविण्यासाठी   हे समीकरण सोडवावे लागते.

अंतराल आकलन : सांख्यिकीय अनुमानशास्त्रात अंतराल आकलन पद्घतीचे महत्त्व फार मोठे आहे. बऱ्याच वेळा अज्ञात प्रचल θ साठी बिंदू आकलकाऐवजी एक अंतराल सूचित केला जातो. या पद्घतीसअंतराल आकलन असे म्हणतात. ह्या पद्घतीत θ_L (X₁, X₂,… , X_n )आणि θ_U ((X₁, X₂,…. , X_n ) हे दोन यदृच्छ चल, (θ_L &lt θ_U) असेअसतात की, P_r [ θ_L≤θ≤θ_U ] =(1−α). येथे [ θ_L, θ_U ] ह्या यदृच्छ अंतरालास विश्वास अंतराल असे म्हणतात. θ_Lआणि θ_Uह्यांस अनुक्रमे निम्न विश्वास सीमा आणि ऊर्ध्व विश्वास सीमा असे म्हणतात. ( 1−α) ह्यास विश्वासांक असे संबोधतात. वरील संभाव्यता विधानात अज्ञातप्रचल θ  हास्थिर असून [θ_L , θ_U] ह्या चल अंतरालात θ समाविष्ट होण्याची संभाव्यता ( 1−α) असते. सर्वसाधारणपणे αचेमूल्य 0·01, 0·05 किंवा 0·1 असे निवडले जाते. उदा., जर X₁, X₂,…. , X_n हा n ह्या आकारविस्ताराचा N ( θ, σ²) ह्या प्रसामान्य वंटन फलनातून घेतलेला प्रतिदर्श असेल आणि θव σ² हे अज्ञात प्रचल असतील तर 100 ( 1−α)% विश्वासांक असलेला θ  Mm विश्वास अंतरालखालीलप्रमाणे असतो. 

आणि t_{(α/2, n–1)}हा (n –1) मुक्तमात्रा असलेल्या t – वंटन फलनाचा ऊर्ध्व α/ २ बिंदू असतो जो t – वंटन फलनाच्या कोष्टकातून उपलब्ध होतो [⟶ वंटन सिद्घांत]. 

बेझियन अनुमानशास्त्र : थॉस बेझ ह्या इंगज धर्मपदेशकाने अठराव्या शतकात संभाव्यता सिद्घांतावर केलेल्या कामामुळे बेझियन ही संज्ञा वापरात आली. ही पद्घत व्यक्तिनिष्ठ संभाव्यतेवर अवलंबून असते. बेझ आकलन पद्घतीत प्रचल θ संबंधीजी काही पूर्वप्राप्त माहितीउपलब्ध असते तिचा वापर केला जातो. ही पूर्वप्राप्त माहिती पूर्वप्राप्तवंटन फलन h ( θ) च्या स्वरूपात मांडली जाते. जर X₁ , X₂ , … , X_n हा f ( x θ) ह्या संभाव्यता घनता-फलनातून घेतलेला n आकारविस्ताराचा प्रतिदर्श असेल तर बेझ आकलन पद्घतीत पूर्वप्राप्त वंटन फलन h ( θ) आणि प्रतिदर्शात उपलब्ध असलेल्या माहितीच्या आधारे प्रचल θचेउत्तरप्राप्त वंटन फलन काढले जाते. बेझ आकलनपद्घती ही उत्तरप्राप्त वंटन फलनावर आधारलेली असते. उदा., जरX₁ , X₂ , … , X_n हा B ( 1, θ) ह्या बेर्नुली संभाव्यता घनता-फलनातून घेतलेला प्रतिदर्श असेल आणि θ ह्याअज्ञात प्रचलाचे पूर्वप्राप्तसंभाव्यता घनता-फलन 

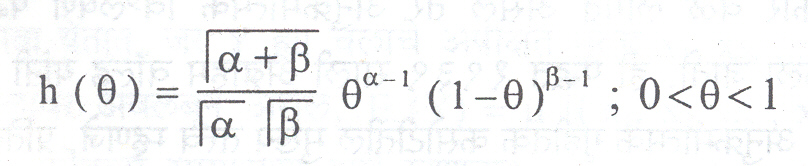
हे बीटा वंटन फलन असेल, तर θ चेउत्तरप्राप्त संभाव्यता घनता-फलन 

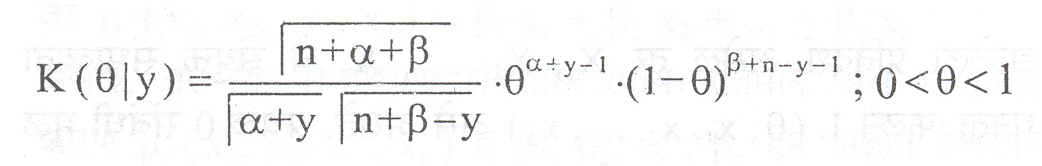
हे सुद्घा बीटा वंटन फलन असते. त्रुटि-वर्ग व्यय फलनाद्वारे प्रचल θ चेबेझ आकलन पद्घतीने काढलेले आकल खालीलप्रमाणे असते. 

बेझ आकलक ω  (y) हे प्रचल θचेमहत्तम शक्यता आकलक y | n आणि पूर्वप्राप्त संभाव्यता फलनाचे माध्य यांच्या भारित सरासरी एवढे  

आहे. 

प्रचलात्मक गृहीतक परीक्षण कसोट्या : हा सांख्यिकीयअनुमानशास्त्राचा महत्त्वाचा विभाग आहे. ह्यात सांख्यिकीय गृहीतकांचातौलनिक अभ्यास केला जातो. प्रचलात्मक कसोट्यांमध्ये समष्टीच्यासंभाव्यता घनता-फलनाचे स्वरूप f ( x θ) हे माहीत असणे जरू रअसते. संभाव्यता घनता-फलनाच्या प्रचल θ  संबंधीजे विधान केलेलेअसते त्यास सांख्यिकीय गृहीतक असे म्हणतात. ही गृहीतके दोनप्रकारांची असतात. गृहीतकाद्वारे जर सर्व अज्ञात प्रचलांची पूर्ण माहितीअधोरेखित होत असेल तर त्यास साधे गृहीतक असे म्हणतात. जरप्रचलांसंबंधी अपूर्ण माहिती अधोरेखित होत असेल तर त्यास संमिश्रगृहीतक म्हणतात. गृहीतक परीक्षण कसोटीसाठी मूळ गृहीतक व पर्यायी गृहीतक अशी दोन गृहीतके लागतात. गृहीतक परीक्षण कसोटीद्वारे एकनियम मिळतो. त्याचा वापर करून मूळ गृहीतकाचा स्वीकार करावयाचाका पर्यायी गृहीतकाचा स्वीकार करावयाचा हे ठरविले जाते. ही क्रि यायदृच्छ प्रतिदर्शाच्या साहाय्याने केल्याने त्यात दोन प्रकारच्या त्रुटी राहूशकतात. जर मूळ गृहीतक योग्य असूनसुद्घा त्याज्यठरविले गेले तरत्यास प्रथम प्रकारची त्रुटी असे म्हणतात. जर पर्यायी गृहीतक योग्यअसता मूळ गृहीतक स्वीकारले गेले, तर त्यास द्वितीय प्रकारची त्रुटीअसे म्हणतात. गृहीतक परीक्षणासाठी जो नियम वापरावयाचा त्याद्वारेदोन्ही प्रकारच्या त्रुटींची संभाव्यता लघुतम व्हावयास पाहिजे. परंतु जेव्हाप्रतिदर्शाचा आकारविस्तार पूर्वनियोजित असतो तेव्हा दोन्ही प्रकारच्यात्रुटींची संभाव्यता एकाचवेळी लघुतम करता येत नाही. एका प्रकारच्यात्रुटीची संभाव्यता कमी केल्यास दुसऱ्या प्रकारच्या त्रुटीची संभाव्यतावाढू लागते. नेमन आणि पीअर्सन यांनी शोधून काढलेल्या कसोटीपद्घतींत प्रथम प्रकारच्या त्रुटीची संभाव्यता एका विशिष्ट सार्थता पातळीवरमर्यादित ठेवून द्वितीय प्रकारच्या त्रुटीची संभाव्यता लघुतम केली जाते,जेणेकरून त्या कसोटीची शक्ती महत्तम केली जाते. ह्या पद्घतीमध्येप्रतिदर्शाच्या अवकाशाचे दोन विभाग पडतात. एका विभागास स्वीकृति-क्षेत्र म्हणतात तर दुसऱ्या विभागास विवेचक-क्षेत्र असे म्हणतात. यादोन विभागांची निर्मिती प्रथम प्रकारच्या त्रुटीच्या संभाव्यतेवर अवलंबूनअसते. नेमन-पीअर्सन पूर्वप्रमेय खालीलप्रमाणे मांडता येते. 

---

नेमन-पीअर्सन पूर्वप्रमेय : जर X_१, X_२, … , X_n हा n ह्या आकारविस्ताराचा f ( x θ) ह्या संभाव्यता घनता-फलनापासून प्राप्तझालेला प्रतिदर्श असेल तर X_१, X_२, … , X_n चे संयुक्त संभाव्यताघनता-फलन L (θ X_१, X_२, … , X_n) असे असते. प्रचल θ संबंधीमूळगृहीतक जर H₀ : θ= θ₀ असेल आणि पर्यायी गृहीतक H₁ : θ= θ₁ असेल, C हा प्रतिदर्शाच्या अवक्राशाचा उपसंच असेल, k हा स्थिर बिंदू असेल आणि

                                           जर निरीक्षित प्रतिदर्श (X₁, X₂,…. , X_n )ÎC

                                         जर निरीक्षित प्रतिदर्श (X₁, X₂,…. , X_n )ÎC* 

(इ) α= Pr [(X₁, X₂,…. , X_n ) ÎC H₀]

तर C ह्या उपसंचास उत्तम विवेचक-क्षेत्र असे म्हणतात. येथे αकसोटीची सार्थता पातळी दर्शविते व C* हा C चा पूरक संच असतो. जर निरीक्षित प्रतिदर्श (X₁, X₂,…. , X_n) विवेचक-क्षेत्र C मध्ये असेल तर मूळ गृहीतक H₀ : θ= θ₀त्याज्यठरविले जाते व पर्यायी गृहीतकH₁ : θ= θ₁ हे स्वीकारले जाते. ही कसोटी जेव्हा मूळ आणि पर्यायी गृहीतके साधी असतात तेव्हा वापरली जाते. उदा., जर X₁, X₂,…. , X_n हा n ह्या आकारविस्ताराचा N ( θ, १) ह्या प्रसामान्य वंटन फलनातून घेतलेला प्रतिदर्श असेल आणि जर का आपणास मूळ गृहीतक H₀ : θ= 0 विरुद्घ पर्यायी गृहीतक H₁ : θ= 1, हे तपासावयाचे असेल तर 

संच  हे उत्तम विवेचन-क्षेत्र असते. येथे c हा स्थिर बिंदू असून त्याचे पुढीलप्रमाणे ठरविले जाते. 

शक्यता गुणोत्तर कसोटी : जर मूळ गृहीतक किंवा पर्यायी गृहीतककिंवा दोन्ही गृहीतके साधी नसून संमिश्र असतील तर शक्यता गुणोत्तरकसोटी वापरली जाते. ह्या कसोटीमध्ये सुद्घा समष्टीच्या संभाव्यताघनता-फलनाचे स्वरूप माहीत असणे जरुर असते, जे एक किंवा अनेकअज्ञात प्रचलांवर अवलंबून असते. जर X₁, X₂,…. , X_n हा n ह्याआकारविस्ताराचा f ( x θ₁, θ₂, … , θ_r) ह्या संभाव्यता घनता-फलनातून घेतलेला प्रतिदर्श असेल, संच Ω समष्टीच्या सर्व प्रचलांचेअवकाश दर्शवीत असेल, ω हाΩ चाउपसंच असेल तर ह्या कसोटीद्वारेआपण खालील प्रकारची गृहीतके तपासू शकतो. 

मूळ गृहीतक H₀ : θÎωविरूद्ध पर्यायी गृहीतक 

H_१: θÎ(Ω–ω). ह्या कसोटीत प्रथम समष्टीचे जे प्रचल असतातत्यांची बिंदू आकलकेमहत्तम शक्यता पद्घतीने काढून शक्यता फलन 

L(Ω)L (Ω) काढले जाते. नंतर मूळ गृहीतक योग्य आहे असे समजून जे प्रचल अज्ञात असतील त्यांची बिंदू आकलके काढून शक्यता फलन L (ω) चे महत्तम मूल्य L (ω) हे काढले जाते आणि खालील λ(X₁, X₂,…. , X_n) हे शक्यता गुणोत्तर विचारात घेतले जाते.

जर λमूल्य अतिशय कमी असेल, λ ≤ λ_o , तर मूळ गृहीतक त्याज्यठरविले जाते व पर्यायी गृहीतक स्वीकारले जाते. येथे λ_oचेमूल्य खालील सूत्राने ठरविले जाते. 

α=Pr [ λ(X₁, X₂, … , X_n ) ≤λ_o H_o ]

येथे αकसोटीची सार्थता पातळी दर्शविते. ह्या कसोटीद्वारे अनेक गृहीतकेतपासली जातात. उदा., जर X₁, X₂, … , X_n हा n ह्या आकारविस्ताराचा N ( θ₁, θ₂ ) ह्या प्रसामान्य वंटनातून घेतलेला यदृच्छ प्रतिदर्श असेल, तर प्रचल θ₁ आणि θ₂ ह्यांचे अवक्राश खालीलप्रमाणे लिहिता येते. 

Ω ={ ( θ₁, θ₂ ) −∞&lt θ₁ &lt∞ 0 &lt θ₂ &lt∞}

जर मूळ गृहीतक H₀ : θ₁ =०, θ₂ &gt 0 विरुद्घ पर्यायी गृहीतक H₁ : θ₁ = 0, θ₂ &gt 0. हे तपासावयाचे असेल तर  

ω ={ ( θ₁, θ₂ ) θ₁ = 0 0 &lt θ₂ &lt ∞}

हा मूळ गृहीतकाद्वारे दर्शविलेला Ω चाउपसंच असतो. वरील गृहीतकतपासण्यासाठी शक्यता गुणोत्तर कसोटीद्वारे आपणास खालील परीक्षासंख्यानक उपलब्ध होते,

हे (n – 1) मुक्तमात्रा असलेले t – वंटन असते. t – वंटनाचे कोष्टक वापरून मूळ गृहीतक स्वीकारावयाचे का पर्यायी गृहीतक स्वीकारावयाचे यांचा निर्णय घेता येऊ शकतो. 

तसेच जर X₁, X₂, … , X_n आणि Y₁, Y₂, … , Y_m हे अनुक्रमे N ( θ₁, θ₃ ) आणि N ( θ₂, θ₄ ) ह्या प्रसामान्य वंटनापासून घेतलेले n आणि m आकारविस्ताराचे दोन निरवलंबी यदृच्छ प्रतिदर्श असतीलतर सर्व प्रचलांचे अवक्राश खालीलप्रमाणे लिहिता येते. 

---

           Ω ={ ( θ₁, θ₂θ₃ θ₄) −∞&lt θ₁θ₂&lt∞ 0 &lt θ₃ θ₄ &lt∞}

जर गृहीतक H₀ : θ₃ = θ₄ विरुद्घ H₁ :θ₃ =θ₄ हे तपासावयाचे असेल तर  ={ ( θ₁, θ₂, θ₃, θ₄ ) −∞&lt θ₁, θ₂ &lt∞, 0 &lt θ₃=θ₄ &lt∞}

हा मूळ गृहीतकाद्वारे दर्शविलेला Ωचा उपसंच असतो आणि वरीलगृहीतक तपासण्यासाठी शक्यता गुणोत्तर कसोटीद्वारे खालील परीक्षा 

संख्यानक उपलब्ध होते. 

हे (n – 1) आणि ( m – 1) मुक्तमात्रा असलेले F – वंटन असते. F– वंटनाचे कोष्टक वापरून मूळ गृहीतक योग्य वा अयोग्य हे ठरविता येते. 

अनुकमात्मक विश्लेषण : सर्व प्रचलात्मक आणि अप्राचलात्मक पद्घतीत प्रतिदर्शाचा आकारविस्तार पूर्वनियोजित असतो. काही विशिष्ट परिस्थितीत जर प्रतिदर्शांची निरीक्षणे उपलब्ध होण्यास फार खर्च येत असेल किंवा फार वेळ लागत असेल तर अनुकमात्मक विश्लेषण पद्घतीचा वापर केला जातो. ही पद्घत १९३९ साली अबाहम वॉल्ड यांनी शोधून काढली. अनुकमात्मक गृहीतक कसोटीतील मुख्य तत्त्व म्हणजे, प्रतिदर्शाचा आकारविस्तार पूर्वनियोजित नसतो. ह्या पद्घतीत प्रत्येक निरीक्षणानंतर, (१) मूळ गृहीतकाचा स्वीकार करावयाचा वा (२) पर्यायी गृहीतकाचा स्वीकार करावयाचा वा (३) आणखी एक निरीक्षण घ्यावयाचे हे ठरविणारा एक नियम मांडण्यात येतो. त्यामुळे प्रतिदर्शाचा आकारविस्तार मर्यादित राहतो. [⟶ अनुकमात्मक विश्लेषण].

सहसंबंधाचे विश्लेषण :(X₁,Y₁ ), (X₂, Y₂ ), … , (X _n, Y _n) ह्या यदृच्छ प्रतिदर्शावर आधारित X व Y या दोन चलांधील सहसंबंध Ρचे r हे आकलक खालीलप्रमाणे असते.

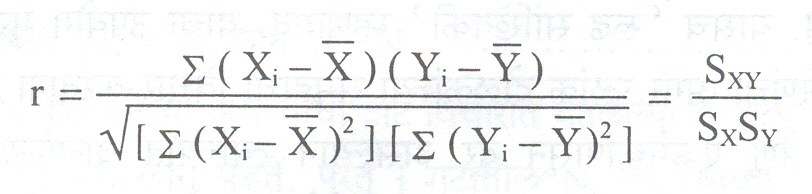
येथे X आणि Y SX, SY ही प्रतिदर्शाची X आणि  Y साठी अनुक्रमे माध्ये आणि प्रमाण विचलने असून S_XY हे सहविचरण आहे.

 

 

जर X आणि Y चे संयुक्त घनता-फलन द्विचल प्रसामान्य असेल, तरΡ चे प्रतिदर्शी वंटन फलन काढता येते हे सर रॉनल्ड एलमर फिशर यांनी १९९५ मध्ये शोधून काढले. त्यानुसार जर का H0:r= 0 विरूद्घ H₁ : r=0 ह्या गृहीतकांचे परीक्षण करावयाचे असेल तर खालील परीक्षा संख्यानक वापरले जाते.

जे ( n – 2 ) मुक्तमात्रा असलेले t – वंटन असते.

समाश्रयण विश्लेषण : समाश्रयण विश्लेषणाचे संख्याशास्त्रात अतिशय महत्त्वाचे स्थान आहे. जेव्हा एखाद्या निरीक्षित चलाचे अपेक्षित मूल्य हे दुसऱ्या चलाचे फलन असते, [जसे, E (Y) μ(x)] तेव्हा समाश्रयण पद्घतीचा वापर केला जातो. ह्यामध्ये फलनाचे स्वरूप माहीत असते, परंतु त्यातील प्रचल अज्ञात असतात. समाश्रयण विश्लेषणात अज्ञात प्रचलांची आकलके काढूनY ह्या अवलंबी चलाबद्दल अनुमान वर्तविले जाते.जर यदृच्छ चल Y आणि x मधील संबंध रेषीय असेल तर तो खालीलप्रमाणे लिहिता येतो.

Y=α+ βx + e

येथे αआणि β हे अज्ञात प्रचल असून त्यांची आकलके लघुतम-वर्ग पद्घतीने काढली जातात.β ह्यास समाश्रयण गुणांक असे म्हणतात.जर 

X₁ , x₂ , … , x_n ह्या ज्ञात मूल्यांना  अनुरूप y₁ , y₂ , … , y_n हा निरीक्षित प्रतिदर्श असेल तर αआणिβ चे आकलक खालीलप्रमाणे असतात.

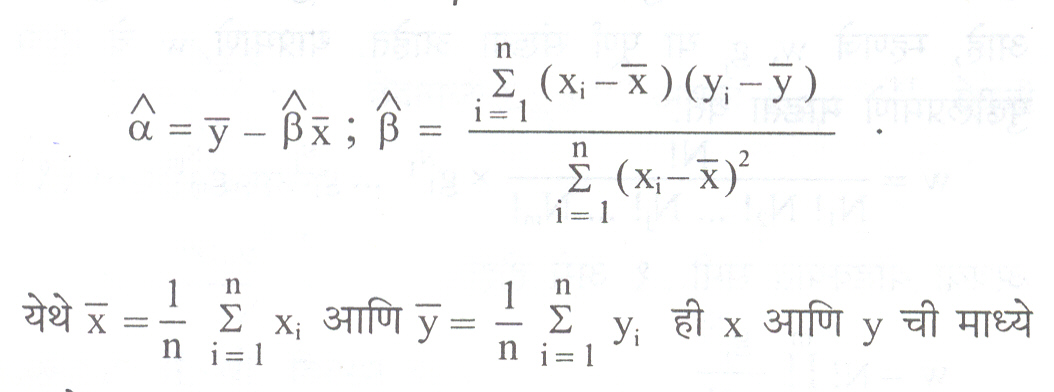आहेत.e ह्या यदृच्छ चलास त्रुटी घटक असे म्हणतात. त्याचे वंटन फलन प्रसामान्यN ( 0 , σ² ) असेल तर,σ² चे आकलक महत्तमशक्यता पद्घतीने काढता येते व त्याचा वापर करून प्रचल αआणिβसाठी अंतराल आकलने काढता येतात आणिαव β संबंधी गृहीतके  तपासता येतात.जर Y ह्या चलाचे अपेक्षित मूल्य x₁, x₂, … , x_p ह्या p चलांवर अवलंबून असेल, E (Y) μ[( x₁, x₂, … , x_p )], तर त्यास अनेकचर समाश्रयण असे म्हणतात. 

जर μX₁ X₂, … , X_p ) β₁ X₁ + β ₂ X₂ + … + β _p X_p असेल, तर त्या समाश्रयण संबंधास रेषीय प्रतिमान असे म्हणतात. कारण( X₁, X₂, … , X_p ) हेβ₁, β₂, … , β_p ह्या अज्ञात प्रचलांचे रेषीय फलन आहे. रेषीय प्रतिमानांच्या विश्लेषणासाठी गौस-मार्कोव्ह सिद्घांताचा वापर केला जातो.रेषीय प्रतिमानांचा वापर सांख्यिकीय अनुमानशास्त्रात व्यापकपणे केला जातो.

पहा :  अनुक्रमात्मक विश्लेषण अप्राचलात्मक पद्घति प्रतिदर्श सर्वेक्षण सिद्घांत वंटन सिद्घांत संभाव्यता.

संदर्भ : 1. Hogg, R. V. Craig, A. T. Introduction to Mathematical Statistics, New York, 1970.

           2. Hogg, R. V. Tanis, E. A. Probability and Statistical Inference, New York, 1989.

           3. Kale, B. K. A First Course on Parametric Inference, 1999.

देशमुख,शैलजा चिं. टिकेकर, व. ग.

“