उपभोक्त्याचे संतोषाधिक्य: एखाद्या वस्तूसाठी किंवा सेवेसाठी उपभोक्ता जास्तीतजास्त जी किंमत द्यावयास तयार असतो ती किंमत व प्रत्यक्ष ज्या किमतीस ती वस्तू किंवा सेवा त्यास मिळते, ती किंमत, या दोन किंमतींमधील फरक म्हणजेच ‘उपभोक्त्याचे संतोषाधिक्य’. ही कल्पना अर्थशास्त्रात मार्शलने प्रचलित केली असली, तरी तिचा उगम द्यूप्यूई (१८०४–१८६६) या फ्रेंच अभियंत्याने
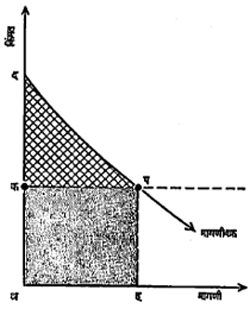
१८४४ मध्ये प्रसिद्ध केलेल्या एका प्रबंधात आढळतो. उपभोक्ता एखाद्या वस्तूसाठी जी किंमत देतो, तीवरून त्या वस्तूची त्यास असलेली संपूर्ण उपयोगिता मोजता येणार नाही, हे द्यूप्यूईने पुलासारख्या सार्वजनिक कामाची उपयोगिता कशी मोजावी याचे विवेचन करताना प्रतिपादिले. मार्शलच्या मते जेव्हा उपभोक्ता बाजारातील किंमतीस एखादी वस्तू खरीदतो, तेव्हा सामान्यतः त्यास संतोषाधिक्य लाभते. समजा चहाची किंमत १५ रु. किलो असताना उपभोक्ता एक किलो चहा घेण्यास तयार आहे, पण किंमत १० रु. किलो झाल्यास त्याने आणखी एक किलो चहा खरेदी केला असता. अशा परिस्थितीत पहिल्या किलोसाठी १५ रु. व दुसऱ्या किलोसाठी १० रु. असे एकूण २५ रु. देण्याची त्याची तयारी असते पण प्रत्यक्षात त्याला दोन किलो चहा फक्त २० रुपयांतच मिळतो म्हणजे त्याला ५ रु. संतोषाधिक्य लाभते असे म्हणता येईल. उतरत्या सीमांत उपयोगितेच्या सिद्धांतानुसार वस्तूचा दरेक एकक कमी कमी किंमतीसच उपभोक्ता द्यावयास तयार होईल. सीमांत एककाची उपयोगिता एककाच्या किंमती पेक्षा कमी झाली की, तो खरेदी करणे थांबवील. सीमांत एककासाठी द्याव्या लागणाऱ्या किंमतीसच अगोदरचे एकक विकत घेता येत असल्यामुळे उपभोक्त्यास संतोषाधिक्य लाभते. याचाच अर्थ काही परिमाणांत वस्तू खरेदी करण्यापासून उपभोक्त्यास मिळणारा संतोष, त्याने दिलेल्या रकमेमुळेत्याचे जे समाधान नष्ट होते, त्यापेक्षा अधिक असतो. मीठ, वृत्तपत्रे, पोस्टाची तिकिटे, काड्यापेट्या यांसारख्या वस्तूंपासून उपभोक्त्याला मोठ्या प्रमाणावर संतोषाधिक्य लाभते, कारण ह्या वस्तू अतिशय उपयुक्त असूनही त्यांची किंमत अत्यल्प असते. खालील आकृतीवरून हे विवेचन स्पष्ट होते. ‘अक’ या किंमतीस ‘अह’ इतकी मागणी असेल. वस्तूच्या ‘अह’ इतक्या परिमाणासाठी उपभोक्त्याची जास्तीत जास्त किंमत देण्याची तयारी ‘अहपद’ या क्षेत्रफळाने दर्शविली जाते. ‘अक’ किंमतीस ‘अह’ परिमाणासाठी प्रत्यक्ष द्यावी लागणारी किंमत ‘अहपक’ या क्षेत्रफळाइतकी आहे. याचाच अर्थ ‘पकद’ हा त्रिकोण उपभोक्त्याचे संतोषाधिक्य दर्शवितो. अर्थशास्त्रातील अनेक प्रश्नांचा उलगडा करण्यासाठी संतोषाधिक्याच्या कल्पनेचा वापर करण्यात आला आहे. उदा., मार्शलने या कल्पनेच्या आधारे असे सुचविले की, उतरत्या उत्पादन फलांच्या उद्योगांवर कर बसवून वाढत्या उत्पादन फलांच्या उद्योगांना उपदान देणे अधिक हितकर होऊ शकेल. काहींचे असेही मत आहे की, वस्तूवरील करांच्याऐवजी प्राप्तिकर उपभोक्त्यांना जास्त सोईस्कर होईल.
संतोषाधिक्याच्या या कल्पनेसंबंधी अर्थशास्त्रज्ञांमध्ये बरेच वादविवाद झाले आहेत. काहींच्या मते ही कल्पना अवास्तव आहे. तिचा उपयोग करताना काही गृहीतकृत्ये मानावी लागतात. काहींना वाटते की, संतोषाधिक्याचे बिनचूक आर्थिक मापन करता येत नसल्यामुळे ही कल्पना निरुपयोगी आहे. अलीकडे हिक्स यांनी समतुष्टी वक्राच्या आधारे या कल्पनेस मूर्त स्वरूप देण्याचे प्रयत्न केले आहेत. त्यामुळे जरी विवेचनात अधिक स्पष्टता आली असली, तरी सर्वच वाद मिटलेले नाहीत. संतोषाधिक्य बिनचूक मोजणे कितीही कठीण असले, तरी ही कल्पना बऱ्याच सामाजिक प्रश्नांवरील धोरण आखताना उपयोगी पडण्यासारखी आहे, असे सॅम्युएल्सन यांचे मत आहे.
पहा : उपयोगिता कल्याणकारी अर्थशास्त्र मागणी.
सुर्वे, गो. चिं.
“