इलेक्ट्रॉन : अणू हा रासायनिक दृष्ट्या मूलद्रव्याचा लहानात लहान घटक आहे. पण विसाव्या शतकात या अणूचीही विभागणी त्याच्या घटक कणांत (मूलकणांत) करता येते, हा सिद्धांत मान्यता पावला. या शतकांत सर्व अणूंत आढळणारा एक ऋण विद्युत् भारित कण म्हणून इलेक्ट्रॉन प्रसिद्धी पावला.
इलेक्ट्रॉन ही संज्ञा सर्वप्रथम जी. स्टोनी यांनी १८९१ साली विद्युत् भाराच्या एककास उद्देशून वापरली. अशा मूलभूत एककाची कल्पना फॅराडे यांनी विद्युत् विश्लेषणासंबंधी केलेल्या कार्यावरून निघाली.
अत्यंत कमी दाब असलेल्या नळीतील वायूमधून विद्युत् विसर्जन केल्यास ⇨ ऋण किरण मिळतात व या किरणांवरूनच अणूपेक्षाही लहान अशा अत्यंत हलक्या कणाच्या अस्तित्वाची कल्पना शास्त्रज्ञांस आली. ऋण किरण हे वेगाने वाहणाऱ्या कणांचे समुदाय आहेत की तरंग आहेत याबद्दल एकोणिसाव्या शतकाच्या अखेरीस बराच वाद झाला, पण १८९७ च्या सुमारास जे. जे. टॉमसन यांच्या प्रयोगावरून या किरणांच्या कणरूपी सिद्धांतास पुष्टी मिळाली. या प्रयोगावरून सिद्ध झाले की, कशाही रीतीने हे ऋण किरण निर्माण झाले तरी इलेक्ट्रॉनाचा विद्युत् भार e व त्याचे वस्तुमान m यांचे गुणोत्तर e/m याचे मूल्य एकच येते व प्रत्येक कणाचे वस्तुमान हायड्रोजन अणूच्या वस्तुमानाच्या सु. १/१८४० इतके असते. शिवाय हे कण प्रत्येक अणूचे घटक असले पाहिजेत अशी खात्री झाली. यानंतर १०–१५ वर्षांनी कोणताही विद्युत् भार मूलभूत एककांचा बनलेला असतो, असा स्पष्ट पुरावा मिळाला व अशा मूलभूत ऋण विद्युत् भार एककास इलेक्ट्रॉन हे नाव मिळाले. ऋण विद्युत् भार असलेला इलेक्ट्रॉन अणूचा घटक आहे म्हणून अणुगर्भावर (अणुकेंद्रावर) धन विद्युत् भार असावयास पाहिजे हेही स्पष्ट झाले व ही गोष्ट अर्नेस्ट रदरफर्ड यांच्या कार्यावरून सिद्ध झाली.
इलेक्ट्रॉनाच्या विद्युत् भाराचे मापन : हे मापन प्रथमत: एच्. ए. विल्सन व जे. जे. टॉमसन यांनी केले. तसे करताना स्टोक्स यांच्या नियमाची सत्यता त्यांनी गृहीत धरली होती. स्टोक्स यांचा नियम असा आहे : श्यानता (प्रवाहास होणारा विरोध) असलेल्या द्रायूतून (प्रवाही पदार्थातून) गुरुत्वीय प्रेरणेखाली पडणाऱ्या लहान वजनदार गोलाचा वेग वाढत जाऊन अखेरीस एका विशिष्ट मूल्यास स्थिर होतो व या स्थिर मूल्यास अंतिम वेग म्हणतात. विद्युत् भारित जलकणांचा बनलेला छोटा ढग त्याच्या स्वतःच्या वजनामुळे (गुरुत्वीय प्रेरणेमुळे) खाली सरकत असताना विल्सन व टॉमसन यांनी त्याचा अंतिम वेग मोजला व त्यावरून जलकणाच्या त्रिज्येचे मूल्य काढले. ढगातील पाण्याचे वजन व त्यावरील विद्युत् भार माहीत असल्याने एका कणावरील विद्युत् भार काढताआला व हा भार म्हणजे इलेक्ट्रॉनाचा विद्युत् भार होय.
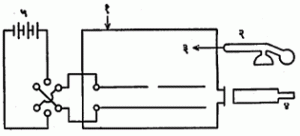
या पद्धतीत सुधारणा करून आर्. ए. मिलिकन यांनीही इलेक्ट्रॉनाच्या विद्युत् भाराचे मापन केले. त्यांनी जलकणाच्या ऐवजी तेलाच्या बारीक थेंबावरील विद्युत् भार मोजला. पाण्याऐवजी तेल वापरण्याचे कारण असे की, प्रयोगाच्या तापमानात पाण्याची वाफ होते व त्यामुळे जलकणांचे आयतन (घनफळ) बदलते, तसे तेलाच्या थेंबांच्या बाबतीत होत नाही. मिलिकन यांचा प्रयोग विश्वसनीय समजला जातो व म्हणून त्याचे वर्णन थोडक्यात पुढे दिले आहे : या प्रयोगात लागणाऱ्या उपकरणाची मांडणी आ. १ मध्ये दाखविल्याप्रमाणे असते. कणित्राच्या साहाय्याने तेलाचे अतिबारीक थेंब प्राप्त होतात व त्यावर विद्युत् भारही येतो. हे थेंब आकृतीमध्ये दाखविलेल्या मार्गाने प्रयोग घटात प्रवेश करतात. हे तेलकण, गुरुत्वाकर्षणामुळे खाली सरकताना अथवा बाहेरून लावलेल्या विद्युत् क्षेत्रामुळे वर सरकताना, प्रकाश योजनेच्या व सूक्ष्मदर्शकाच्या साहाय्याचे स्पष्ट पाहता येतात व त्यांचा सरकण्याचा वेग काढता येतो. हे वेग अनुक्रमे vd व vu समजल्यास
mg = Kvd … … … (१)
व Xq – mg = Kvu … … … (२)
ही समीकरणे मिळतात. यांत m हे तेलकणाचे वस्तुमान असून K हा स्थिरांक आहे व g गुरुत्वीय प्रवेग आहे. K चे स्टोक्स यांच्या सूत्राप्रमाणे मूल्य 6 pha आहे (h = तेलाचा श्यानता गुणांक, a = कणाची त्रिज्या वp=२२/७). q हा कणावरील विद्युत् भार असून X हे विद्युत् क्षेत्र आहे. यावरून
| q = | K | (vd + vu)… … …(३) |
| X |
हा तेलकणावरील विद्युत् भार मिळतो. अथवा वर सरकताना जर तेलकणावरील विद्युत् भारात बदल होऊ शकला, तर
| Xen – mg = KVu1 | } | … … (४) |
| Xem – mg = KVu2 |
ही समीकरणे मिळतात व त्यावरून
| en – em = | K | ( vu1 – vu2 ), |
| X |
| अथवा e = | K | (ª vu) … … (५) |
| X |
हे समीकरण मिळते. वेगबदल ∆ vu व विशिष्ट एकक भाराच्या एक अगर अनेक पटींनी कणावरील विद्युत् भारातील वाढ ∆ e यांतील संगती मिलिकन यांसआढळली व त्यावरून विद्युत् भाराच्या एककाचे अस्तित्वसिद्ध झाले. या एककाचे म्हणजे इलेक्ट्रॉनावरील विद्युत् भाराचे (e) मिलिकन यांनी दिलेले मूल्य –४·७७ × १०-१० इ.एस.यू. [इलेक्ट्रो स्टॅटिक यूनिट, → एकके व परिमाणे] असे होते. पण ते काढताना हवेच्या श्यानता गुणांकाचे मूल्य कमी धरले गेल्याने e चे मूल्य दुरुस्त करता, हल्ली सर्वमान्य झालेले मूल्य e = – ४·८०२ × १०-१० इ.एस.यू. = –१·६ × १०-१९ कुलंब आहे.
इलेक्ट्रॉन विद्युत् भार व त्याचे वस्तुमान यांचे गुणोत्तर: या गुणोत्तराचे व्यवस्थित मापन प्रथम जे. जे. टॉमसन यांनी १८९७ मध्ये केले व त्यापुढील ५० वर्षात या महत्त्वाच्या राशीचे अधिकाधिक अचूकतेने मापन झाले. अशा मापनाची मूलभूत तत्त्वे एकसमान असून तत्संबंधीचा एक प्रयोग पुढे दिला आहे. या प्रयोगातील उपकरणाची मांडणी आ. २ मध्ये दाखविली आहे. उपकरणामध्ये वायूचा दाब १/१०,००० वातावरणीय दाबापेक्षाही कमी

असतो. ऋणग्रापासून निघालेली इलेक्ट्रॉन शलाका (किरणसमूह) धनाग्र दंडगोलाच्या मध्यभागी असलेल्या बारीक छिद्रातून बाहेर पडून अखेरीस अनुस्फुरक (विद्युत् कर्षुकीय ऊर्जेचा किंवा विद्युत् भारित कणांचा भडिमार चालू असताना प्रकाशणाऱ्या) पडद्यावर O या जागी प्रदीप्त बिंदुरूपाने पडते. आकृतीत दाखविलेल्या विद्युत् प्रस्थांमध्ये (पट्ट्यांमध्ये), वरचे अग्र धन राहील अशा तर्हेने विद्युत् क्षेत्र निर्माण केल्यास, इलेक्ट्रॉन शलाकेचे वरच्या अंगास विचलन (सरकणे) घडते. यावरून स्पष्ट होते की, ही शलाका ऋण विद्युत् भारित आहे. या दोन पट्ट्यांमधील वर्चोभेद (विद्युत् स्थितींतील फरक) V असल्यास व त्यांमधील लंब अंतर d असल्यास, विद्युत् क्षेत्राची तीव्रता V/d असते व e विद्युत् भारावरील प्रेरणा Ve/d होते. शलाकेतील इलेक्ट्रॉनांचा वेग v आहे असे समजल्यास व इलेक्ट्रॉनांच्या विद्युत् क्षेत्रातील पथाची लांबी l आहे असे समजल्यास, इलेक्ट्रॉन l/v सेकंद विद्युत् क्षेत्रात राहील. या कालात त्यास ऊर्ध्व (उभ्या) दिशेने Vel / dmv इतका वेग प्राप्त होईल (m = इलेक्ट्रॉनचे वस्तुमान). यामुळे अनुस्फुरक पडद्यावरील शलाकेचे ऊर्ध्व दिशेने होणारे विचलन इतके होईल. पडद्यावर D हे अंतर मोजता येते. L हे पट्ट्या व
| OP≈D = | Vel | ( | L + | L | ) | … …(६) |
| dmv2 | 2 |
पडदा यांमधील अंतर आहे. आता v चे मूल्य ज्ञात झाल्यास समी. (६) वरून e/m चे मूल्य काढता येईल. v चे मूल्य समजण्यासाठी आकृतीच्या प्रतलास (पातळीस) लंब अशा दिशेने व ज्याचा परिणाम l या अंतरावरच होईल असे कर्षुक (चुंबक) क्षेत्र लावले जाते. या क्षेत्राची तीव्रता B आहे असे समजू. या क्षेत्राचा परिणाम म्हणून कर्षुक क्षेत्राची दिशा व इलेक्ट्रॉनांच्या गतीची दिशा या दोहोंसही लंब अशा दिशेने इलेक्ट्रॉन शलाकेचे विचलन होते. म्हणून ती शलाका फ्लेमिंग यांच्या वाम हस्त नियमाप्रमाणे [कर्षुक क्षेत्र, गती आणि विद्युत् चालक प्रेरणा यांच्या दिशांमधील परस्पर संबंध दाखविणाऱ्या नियमाप्रमाणे, → विद्युत्] तिच्या पूर्व स्थानी म्हणजे O येथे परत येते. याचा अर्थ असा की, विद्युत् क्षेत्रामुळे निर्माण झालेली इलेक्ट्रॉनावरील प्रेरणा व कर्षुक क्षेत्रामुळे उत्पन्न झालेली त्यावरील प्रेरणा समान पण विरुद्ध दिशेच्या आहेत. म्हणून
Bev = Ve/d … … … (७)
या समीकरणावरून vचे मूल्य v = V/db मिळते व ते समी.(६) मध्ये घालता e/m चे मूल्य उपलब्ध होते. हे मूल्य प्रयोग नलिकेतील शिलकी वायूच्या जातीवर अगर ऋणाग्राच्या द्रव्यावर अवलंबून नसते, असे प्रयोगांती आढळून आले. धन व ऋण अग्रे [आ. २ मधील (१) व (२)] ह्यांमध्ये वर्चोभेद ठेवण्याऐवजी, ऋणाग्रावर किरणोत्सर्गी द्रव्य (कण वा किरण बाहेर टाकणारे द्रव्य) चोपडले असता, तेथून उत्सर्जित होणाऱ्या बीटा (ß) किरणांच्या [→ किरणोत्सर्ग] शलाकेच्या बाबतीतही हेच e/m चे मूल्य मिळते. यावरून सिद्ध होते की, बीटा किरण शलाका इलेक्ट्रॉनांचीच बनलेली असते. अशा तऱ्हेच्या सर्व प्रयोगांवरून काढलेले e/m चे सर्वसंमत मूल्य १.७६ x१०७ इ. एम. यू./ग्रॅम (इ. एम. यू.- इलेक्ट्रो मॅग्नेटिक यूनिट) असे आहे. e व e/m यांच्या ज्ञात मूल्यांपासून इलेक्ट्रॉनाच्या वस्तुमानाचे (स्थिर वस्तुमानाचे) मूल्य मिळते व ते ९·१०९२ × १०-२८ ग्रॅम म्हणजे हायड्रोजन अणूच्या वस्तुमानाच्या सु. १/१८४० इतके येते. आइन्स्टाइन यांच्या वस्तुमान-ऊर्जा सममूल्यतेच्या तत्त्वाप्रमाणे इलेक्ट्रॉनाच्या वस्तुमानाची सममूल्य ऊर्जा E = mc2= 0.511 Mev एवढी आहे (c प्रकाशवेग, m इलेक्ट्रॉनचे वस्तुमान, Mev दशलक्ष इलेक्ट्रॉन व्होल्ट इलेक्ट्रॉन व्होल्ट म्हणजे १ व्होल्ट वर्चोभेदातून इलेक्ट्रॉन गेल्यास त्याला प्राप्त होणारी ऊर्जा).
किरणोत्सर्गी द्रव्याकडून उत्सर्जित झालेले बीटा किरण हे इलेक्ट्रॉनच असल्याचा उल्लेख मागे आलेला आहे. या बीटा किरणांच्या बाबतीत कॉफ्मन यांना १९०० सालीअसे आढळले की, या किरणांचे e/m हे गुणोत्तर किरणांचावेग वाढला असता कमी होते. याचा अर्थ असा होतो की, वेगात वाढ झाल्यामुळे इलेक्ट्रॉनचे वस्तुमान वाढते व त्यामुळे e/m चे मूल्य कमी होते. ही वस्तुमानातील वाढ आइन्स्टाइन यांच्या मर्यादित सापेक्षता सिद्धांतानुसारहोते : m = mo /√1 – v2/c2 यात mo हे स्थिर वस्तुमान असून vहा त्याचा वेग आहे व c हा प्रकाशवेग आहे. बुखरेर यांनी १९०८ साली वेगवेगळी वेगमूल्ये घेऊन केलेल्या प्रयोगांनी या गोष्टीस पुष्टी मिळाली. पुढील पानावर दिलेल्या कोष्टकावरूनही ही गोष्ट लक्षात येईल.
इलेक्ट्रॉनाचा वेग व त्याचे वस्तुमान यांच्यातील संबंध
| उर्जा
ev |
वस्तुमान
(ग्रॅम) |
वेग
(सेंमी./ सेकंद) |
समान तरंगलांबी
A0 (१०–८सेंमी.) |
| १ | ०·९११ × १०-२७ | ५·९३ × १०७ | १२·२ |
| १०२ | ०·९११ × १०-२७ | ५·९३ × १०८ | १·२२ |
| १०४ | ०·९४१ × १०-२७ | ५·९३ × १०९ | ०·१२१ |
| १०६ | ४·० × १०-२७ | २·८२ × १०१० | ०·००९ |
२·९९८ × १०१० सेंमी. / सेकंद या प्रकाशवेगास इलेक्ट्रॉनाचे वस्तुमान अनंत होईल.
क्षितिज समांतर गती असलेल्या इलेक्ट्रॉनाचे त्याच्या गतीच्या दिशेस लंब असलेल्या एकमूल्य विद्युत् क्षेत्रात प्रवेश केल्यास त्या क्षेत्रातील इलेक्ट्रॉनाचा मार्ग, एखाद्या उंच जागेवरून क्षितिजाला समांतर दिशेने फेकलेल्या दगडाच्या मार्गासारखा, म्हणजे अन्वस्त [एक गणितीय वक्र, → अन्वस्त] असतो. तसेच इलेक्ट्रॉनाच्या गतीस लंब असलेल्या एकमूल्यी कर्षुकीय क्षेत्रामुळे इलेक्ट्रॉनवर लागू होणाऱ्या प्रेरणेची दिशा इलेक्ट्रॉनाच्या गतीस सदोदित लंब रहात असल्याने, कर्षुकीय क्षेत्रातील त्याचा मार्ग वर्तुळाकार असतो.
मुक्त इलेक्ट्रॉन निर्माण होण्याचे काही प्रकार : (१) सर्वसाधारणपणे वायुस्थितीतील अणूंशी होणार्या आयनांच्या (विद्युत् भारित अणू, रेणू किंवा अणूतील मूलकण यांच्या) टकरांमुळे इलेक्ट्रॉन अणूतून बाहेर फेकले जातात व उरलेला अणू धन भारित असतो. यासाठी जरूर असणारे ऊर्जा शोषण दरेक वायूसाठी ठराविक आहे व ते शोषक गुणांक m ने निश्चित केले जाते. m=nA=1/L येथे n ही एकक आयतनातील अणूंची संख्या असून nA हा प्रभावी लंबच्छेद आहे व L हा इलेक्ट्रॉनाचा त्या वायूतील माध्य मुक्त पथ (सरासरी मोकळे अंतर) आहे. बाष्पकोठीमध्ये [आयनीकारक कणांच्या मार्गांचे निरीक्षण करण्यासाठी वापरण्यात येणाऱ्या उपकरणामध्ये, → कण अभिज्ञातक] २ Mev पेक्षा अधिक ऊर्जेमुळे पथाच्या दर सेंटीमीटरास सु. ४० आयनयुग्मे निर्माण होतात असे आढळून आले आहे. (२) तापायनिक उत्सर्जनात (उष्णतेमुळे संवाहकाच्या पृष्ठभागापासून इलेक्ट्रॉन बाहेर पडणाऱ्या क्रियेत) उत्सर्जकाच्या पृष्ठभागातील वर्चस् रोध (ज्या भागात उच्च वर्चसामुळे म्हणजे उच्च विद्युत् स्थितीमुळे कमी ऊर्जा असलेल्या कणांना पुढे जाण्यास रोध होतो असा भाग) उल्लंघण्याइतकी ऊर्जा आतील इलेक्ट्रॉनांना मिळून त्यांचे उत्सर्जन होते. (३) १०७ व्होल्ट/सेंमी. या सुमाराचे विद्युत् क्षेत्र धातूंच्या पृष्ठभागास लावल्यास वर्चस् कूपातून (किमान वर्चसा भोवतालच्या-विहिरीसारख्या-भागातून) इलेक्ट्रॉन बाहेर पडू शकतात व धनाग्राकडे जाऊ पहातात. (४) प्रकाशविद्युत् परिणामामुळे पुरेशी ऊर्जा (hv) असलेले फोटॉन (प्रकाशकणपुंज) अणूतील इलेक्ट्रॉनांवर पडल्यास, त्या इलेक्ट्रॉनांना वर्चस् रोधf उल्लंघून vवेगाने बाहेर पडण्याइतकी ऊर्जा प्राप्त होते हे पुढील समीकरणानुसार घडते : hv = f + ½ mv2. येथे h प्लांक विश्व स्थिरांक आणिv कंप्रता (दर सेकंदास होणारी कंपन संख्या) आहे. (५) किरणोत्सर्गी द्रव्याच्या बीटा किरण ऊत्सर्जनामुळे प्रकाशवेगाच्या २५ ते ९९ पट वेग असलेले इलेक्ट्रॉन मिळतात. (६) एखाद्या अणुगर्भात १·०२२ Mev पेक्षा अधिक ऊर्जा असलेल्या फोटॉनाचा प्रवेश झाल्यास इलेक्ट्रॉन-पॉझिट्रॉन (इलेक्ट्रॉनाइतकेच वस्तुमान असलेला व त्याच्या इतकाच पण धन विद्युत् भार असलेला कण) युग्म बाहेर फेकले जाते. या संबंधीचे भविष्य डिरॅक यांनी प्रथम केले व पॉझिट्रॉनाचे अस्तित्व ॲंडरसन यांनी प्रयोगाने सिद्ध केले. यासंबंधी अधिक माहिती इलेक्ट्रॉन परिवलन (स्वत:च्या अक्षाभोवती किरणे) या संदर्भात पुढे दिली आहे. (७) म्यू मेसॉन या मूलकणाच्या क्षयाच्या अखेरीच्या अवस्थेस इलेक्ट्रॉन, फोटॉन व न्यूट्रिनो (एक विद्युत् भाररहित मूलकण) निर्माण होतात [→ मूलकण].
इलेक्ट्रॉनाची संरचना: इलेक्ट्रॉनाच्या आकाराबद्दल व संरचनेबद्दल अनुमान बांधणे कठीण आहे. रूढ भौतिकीनुसार जे. जे. टॉमसन यांच्या म्हणण्याप्रमाणे गतिमान इलेक्ट्रॉन काही अडथळ्यामुळे थांबल्यास विद्युत् कर्षुकीय प्रारणाचा (ऊर्जेचा) तरंग निर्माण होतो. स्थिर इलेक्ट्रॉनाची त्रिज्याrसमजल्यास इलेक्ट्रॉनास प्राप्त होणारे वस्तुमान पूर्णपणे विद्युत् कर्षुकीय असते व
| ते m = | 2 e2 | इतके असते. यावरून r चे मूल्य मिळते व ते सु. १०-१३ सेंमी. येते. |
| 3 r |
खूप ऊर्जा असलेले इलेक्ट्रॉन अणूच्या आत प्रवेश करू शकतात व अणुगर्भाच्या क्षेत्रातून जाताना त्यांचा वेग वाढतो आणि पथ वक्र होतो. त्यांच्या गतिज ऊर्जेचा काही भाग फोटॉनरूपाने (ब्रेम्सस्ट्राहलुंग म्हणजे प्रतिबंधक प्रारण रूपाने) उत्सर्जित होतो व इलेक्ट्रॉनाची गती प्रतिबंधक लावल्याप्रमाणे कमी होते. अणुगर्भाची ही प्रतिबंधक क्रियाइलेक्ट्रॉनाची जलद गती कमी करण्याची एक प्रमुख यंत्रणा आहे. या उत्सर्जित उर्जेचा परिणाम म्हणून क्ष-किरण नलिकेपासून उत्सर्जित होणाऱ्या शुभ्र अथवा अखंड प्रारणाची पार्श्वभूमी तयात होते.
आतापर्यंत इलेक्ट्रॉनाच्या कणरूपाचाच विचार झाला. त्याच्या तरंगरूपाचा विचार आता करू. द ब्रॉग्ली यांनी १९२४ साली मांडलेल्या विवेचनाप्रमाणे mv हा संवेग(वस्तुमान × वेग)असलेल्या तरंगलांबी l = h/mv इतकी असते. येथे h हा प्लांक विश्व स्थिरांक असून त्याचे मूल्य ६·६२३७७ × १०-२७ ± ०·०००१८ अर्ग-सेकंद आहे. ६० KV या प्रवेगक (वेग वाढविणाऱ्या) विद्युत् दाबामुळे वेग प्राप्त झालेल्या इलेक्ट्रॉनाची तरंगलांबी सु. १/२० A° एवढी असते. इलेक्ट्रॉनाच्या या तरंगरूपास लागू पडेल असे समीकरण श्रोडिंजर यांनी मांडले ते असे :
| d2 ψ | + | 8p2 | (E.V.) ψ = 0 … … (८) |
| dx2 | h2 |
यात E ही इलेक्टॉनाची संपूर्ण ऊर्जा असून, ज्या क्षेत्रात त्याचा प्रवास चालू आहे त्या क्षेत्रामुळे उद्भवलेली V ही स्थितीज ऊर्जा आहे व ψ हे तरंगाच्यापरमप्रसराचे (स्थिर स्थितीपासून होणाऱ्या महत्तम विचलनाचे) फलन (परस्पर संबंधदर्शक राशी) आहे. एखाद्या विवक्षित ठिकाणी इलेक्ट्रॉन असण्याची संभाव्यता |ψ|2 ने दर्शविली जाते.यांच्या ] अनिश्चिततेच्या तत्त्वाप्रमाणे इलेक्ट्रॉन असण्याचे स्थान व त्याचा संवेग यासंबंधी संभाव्यतेच्या भाषेतच बोलणे जरूर आहे.
इलेक्ट्रॉन व पदार्थ यांचा संबंध : उपलब्ध झालेल्या एकंदर माहितीवरून दिसते की, इलेक्ट्रॉन अत्यंत स्थिर आहे. अणूचे आयतन जवळजवळ त्याच्या अणुगर्भाभोवतीच्या इलेक्ट्रॉन ढगानेच व्यापलेले असते, कारण अणूच्या आयतनाचा अत्यंत सूक्ष्म भाग अणुगर्भ व्यापतो. द्रव्याचे रासायनिक गुणधर्म त्याच्या अणूतील इलेक्ट्रॉनांमुळेच ठरतात. इलेक्ट्रॉन फेर्मी-डिरॅक सांख्यिकीचे [→ सांख्यिकीय भौतिकी] नियम पाळतात व म्हणून पुष्कळदा त्यास फेर्मिऑन म्हणतात. इलेक्ट्रॉन-समुदायाला इलेक्ट्रॉन वायू म्हणण्याचा प्रघात आहे. इलेक्ट्रॉन पाउली यांचे विवर्जन तत्त्व [→ अणु व आणवीय संरचना] पाळतात.
समतोल अवस्थेत अणुगर्भाभोवती निरनिराळ्या कक्षांतून इलेक्ट्रॉन परिभ्रमण करीत असतात व काही कारणाने ही समतोल अवस्था बिघडली असता, ते इलेक्ट्रॉन एका भ्रमणकक्षेतून दुसऱ्या भ्रमणकक्षेत उडी मारतात आणि याचा परिणाम म्हणून पुंज (क्वांटम) रूपाने ते प्रारण (तरंगरूपी ऊर्जा) बाहेर टाकतात अगर शोषतात. प्रारण वर्णपट या कारणानेच उद्भवतो. इलेक्ट्रॉनाच्या सर्वांत बाहेरील भ्रमणकक्षेतील इलेक्ट्रॉन संख्येवर द्रव्याची संयुजा अवलंबून असते [→ संयुजा]. त्या कक्षेत एकच इलेक्ट्रॉन असल्यास तो बाहेर फेकला जाऊन उरलेला अणुभाग धन आयन म्हणून राहतो. या उलट त्या कक्षेत सात इलेक्ट्रॉन असल्यास, बाहेरून एक इलेक्ट्रॉन कक्षेच्या आत घेऊन, तेथील इलेक्ट्रॉनांची संख्या आठ करण्याकडे पदार्थाची प्रवृत्ती असते व अशा रीतीने ऋण आयन तयार होतो.
इलेक्ट्रॉन परिवलन : प्रत्येक मूलकणास त्याच्या अक्षाभोवतीच्या परिभ्रमणामुळे विशिष्ट कोनीय परिवलन प्राप्त होते. इलेक्ट्रॉनच्या बाबतीत हे परिवलन
| (कोनीय संवेग) | 1 | x | H | इतके असते. |
| 2 | 2p |
इलेक्ट्रॉनांना + व – अशा दोन परिवलन अवस्था असतात. वर्णपटाच्या संरचनेचे तपशीलवार स्पष्टीकरण होण्यासाठी इलेक्ट्रॉनच्या परिवलनाची व कर्षुकीय परिबलाची (एखाद्या अक्षाभोवती वस्तू फिरविण्याच्या प्रेरणेच्या क्षमतेची) आवश्यकता १९२५ मध्ये ऊलेनबेक व गाउडश्मिट यांनी प्रतिपादिली. इलेक्ट्रॉनाच्या परिवलनामुळे वर्णपटातील कर्षुकीय गुणधर्मासंबंधी उद्भवलेल्या बऱ्याच अडचणींचे निराकरण होऊ शकते. रेणवीय वर्णपटात काही ठिकाणी रेषासमुच्चय आढळतात. उदा., सोडियम रेषाद्वय (रेषांच्या जोड्या). तत्त्वत: या दोन रेषा दोन ऊर्जा प्रतले (म्हणून दोन स्थिर अवस्था) दाखवतात [→ वर्णपटविज्ञान]. ऊलेनबेक व गाउडश्मिट यांच्या प्रतिपादनाच्या आधी, वर्णपट स्पष्टीकरणार्थ तेव्हा वापरात असणारे पुंजांक (पुंजावस्थेचे लाक्षणिक पूर्णांक) n, l व ml यांचाच फक्त उपयोग केल्यास, अवघे एकच ऊर्जा प्रतल मिळते. म्हणून या तीन पुंजांकांखेरीज चवथ्या म्हणजे परिवलन पुंजांकाची (ms) आवश्यकता भासली [→ अणु व आणवीय संरचना]. शिवाय कर्षुकीय आविष्काराच्या दृष्टीने इलेक्ट्रॉन परिवलनाचे महत्त्व असे की, लोहकर्षुकत्व हे कक्षीय कर्षुकीय परिबलापेक्षा, परिवलनामुळे प्राप्त झालेल्या कर्षुकीय परिबलामुळेच उद्भवते, कारण पदार्थाच्या घन अवस्थेत स्फटिकीय विद्युत् क्षेत्रामुळे कक्षीय कर्षुकीय परिबलाचे शमन होते [→ चुंबकत्व].
सापेक्षता सिद्धांताप्रमाणे ऊर्जा व संवेग यांना चतुर्घटक सदिशाचे अवयव समजले जाते [→ सापेक्षता सिद्धांत]. स्थिर वस्तुमान m च्या बाबतीत त्या दोन राशींचा संबंध
(E2/ c2) – p2 = m2c2 … … (९)
या समीकरणाने दाखवला जातो. यापासून मिळणारे तरंगीय समीकरण पुढे दिल्याप्रमाणे येते:
| 1 | ∂2 ψ | – Ñ2 ψ + | 4p2 m2 c2 | ψ = o … (१०) |
| c2 | ∂2 t2 | h2 |
हे समीकरण श्रोडिंजर यांनी १९२६ मध्ये प्रथमत: मांडले, पण त्यास क्लाईन-गॉर्डन समीकरण म्हणतात. या समीकरणाचा निर्वाह (समीकरण सोडवून येणारे उत्तर) डिरॅक यांनी १९२८ साली दिला. यासाठी त्यांनी समी. (१०) वर्गमूळ स्वरूपात मांडले ते असे:
| ir∂ | 1 ∂ ψ | – i (r. Ñ) ψ+ | 2p m c | Ψ= o … (११) |
| c ∂ t | h |
कोणत्याही राशीचे वर्गमूळ घेतल्यास त्या वर्गमूळास + व – ही दोन्ही लागू पडतात याचा अर्थ असा होतो की, इलेक्ट्रॉनाच्या धन ऊर्जेच्या प्रत्येक अवस्थेस अनुलक्षून त्या समान ऋण ऊर्जेची अवस्था असते व म्हणून एका विशिष्ट संवेगाच्या अवस्था दुप्पट होतात. सुरुवातीस यामुळे अडचणीची परिस्थिती उद्भवली खरी, पण डिरॅक यांनी त्याचे संगतवार निराकरण केले ते असे : ज्या अर्थी इलेक्ट्रॉन पाउली यांचे विवर्जन तत्त्व पाळतात, त्या अर्थी ऋण ऊर्जेच्या सर्व अवस्था भरल्या गेल्या आहेत असे मानण्यास हरकत नाही म्हणजे डिरॅक यांनी वर्णन केल्याप्रमाणे जणू काय ऋण ऊर्जेचा समुद्र पसरला आहे, असे चित्र उभे राहते. आता ऋण ऊर्जा अवस्थेतून धन ऊर्जा अवस्थेत इलेक्ट्रॉनाचे स्थित्यंतर होणे याचा अर्थ त्या समुद्रात एक लहान खळगा तयार झाला असा होतो. परिणामत: दोन करण, एक ऋण ऊर्जा-अवस्था अनुरूप इलेक्ट्रॉन व दुसरा धन ऊर्जाअवस्था अवस्था अनुरूप खळगा, निर्माण होतात. या खळग्यासच डिरॅक यांनी पॉझिट्रॉन हे नाव दिले. अर्थात हे स्पष्टच आहे की, पॉझिट्रॉन म्हणजे धन भार असलेला इलेक्ट्रॉनच त्याचा विद्युत् भार +e असून त्या भाराचे व e/m चे मूल्य इलेक्ट्रॉनाप्रमाणेच आहे. इलेक्ट्रॉन- पॉझिट्रॉन युग्माच्या निर्मितीसंबंधी वर दिल्याप्रमाणे डिरॅक यांची उपपत्ती आहे. इलेक्ट्रॉन व पॉझिट्रॉन यांचा परस्पर संबंध कण व प्रतिकण यांच्या जातीचा आहे आणि हा संबंध सर्वसाधारणपणे मूलकणांच्या बाबतीत लाक्षणिक असाच आहे.
डिरॅक यांच्या सिद्धांताचा परिणाम म्हणून एका विशिष्ट संवेगाच्या चार संगत अवस्था होतात व प्रत्येक कणास (इलेक्ट्रॉन) व प्रतिकणास (पॉझिट्रॉन)
| ms = ± ½ x | h | अशा दोन परिवलन अवस्था प्राप्त होतात. |
| 2p |
पॉझिट्रिनाचा प्रत्यक्ष शोध अँडरसन यांनी १९३२ मध्ये लावला, हा उल्लेख मागे आलेलाच आहे. पॉझिट्रॉन अल्पायू असून इलेक्ट्रॉनाशी त्याचा संयोग झाल्याने त्या दोघांच्या ऐवजी दोन फोटॉन बाहेर पडतात. अणुगर्भाभोवतीच्या कक्षांतील इलेक्ट्रॉनांच्या परिभ्रमणामुळे कर्षुकीय परिबल निर्माण होते व त्याचे मूल्य eh/4pmc या बोर मॅग्नेट्रॉनाच्या (कर्षुकीय परिबलाचे एकक = ०·९२७ × १०–२०अर्ग/ओर्स्टेड) पूर्णांक पटीत असते. कोनीय परिबल व कर्षुकीय परिबल यांच्या गुणोत्तरास घूर्ण कर्षुकीय गुणोत्तर p म्हणतात. p = 2 m/ge यात gहा लांडे गुणक आहे. याच्या प्रायोगिक मूल्यावरून कर्षुकीय गुणधर्म फक्त कक्षीय परिभ्रमणामुळे (g = 1) वा फक्तपरिवलनामुळे (g = 2) अथवा दोहोंच्या संमिश्रणामुळे उद्भवतात, हे कळते.
इलेक्ट्रॉन विवर्तन : इलेक्ट्रॉनांची बारीक शलाका स्फटिकावर पडली असता इलेक्ट्रॉनांचे प्रकीर्णन (विखुरणे) होते व हे प्रकीर्णन स्फटिकातील अणूंच्या रचनेवर अवलंबून असते. या गोष्टीसच इलेक्ट्रॉन विवर्तन म्हणतात. असे विवर्तन घडणे हा इलेक्ट्रॉनाच्या तरंगरूपाचा पुरावाच होय, कारण दृश्य प्रकाश व क्ष-किरण यांच्या विवर्तनाचे स्पष्टीकरण ते तरंगरूप आहेत असे मानूनच दिले जाते. इलेक्ट्रॉनाला त्याच्या वेगाप्रमाणे तरंगलांबी (l) असते हे मागे सांगितलेच आहे : l = h / mv = √150/V × 1·008 × 10-8 सेंमी. येथे V हा इलेक्ट्रॉनाला वेगवान करण्यासाठी लावलेला विद्युत् दाब आहे. १९२८ मध्ये जी. पी. टॉमसन यांनी सु. ४०,००० व्होल्ट विद्युत् दाब लावून वेगवान केलेले इलेक्ट्रॉन धातूच्या पातळ पत्र्यावर टाकले व त्याच धातूवर क्ष-किरण वापरून मिळणाऱ्या सममध्य कड्यांसारख्या विवर्तन आकृत्या त्यांना मिळाल्या. या इलेक्ट्रॉनांची तरंगलांबी ०·०६ × १०-८सेंमी. म्हणजे नेहमीच्या क्ष-किरणांच्या तरंगलांबीच्या १/१० इतकी होती. कड्यांचा व्यास स्फटिकातील प्रतलाप्रतलांतील अंतरांवर व इलेक्ट्रॉनांच्या तरंगलांबीवर अवलंबून असतो आणि विवर्तनासंबंधी क्ष-किरण पाळतात तोच ब्रॅग यांचा नियम [→ क्ष-किरण] येथेही लागू पडतो. क्ष-किरण आणि इलेक्ट्रॉन यांच्या विवर्तनातील महत्त्वाचा फरक इलेक्ट्रॉनांच्या कमी असलेल्या पारगम्यतेमुळे (एखाद्या माध्यमातून आरपार जाण्याच्या गुणामुळे) उद्भवतो. म्हणून विरळ पदार्थांच्या बाबतीत इलेक्ट्रॉन अधिक संवेदनक्षम आहेत व या कारणानेच वायू व पृष्ठभागातील काही अणुजाडीचे पातळ थर यांचा अभ्यास करण्यासाठी क्ष-किरणांपेक्षा इलेक्ट्रॉनच अधिक वापरले जातात, तर स्फटिकांच्या अभ्यासासाठी क्ष-किरण अधिक प्रमाणात वापरतात. अभ्यासावयाचा पदार्थ १०-५ सेंमी. पेक्षा कमी जाडीचा असल्यास, वेगयुक्त इलेक्ट्रॉन शलाका त्यावर पाडून ती पदार्थाच्या आरपार जाऊन बाहेर पडल्यानंतर अभ्यासिली जाते, तर यापेक्षा पदार्थ जाड असल्यास, त्याच्या पृष्ठभागावरून २–३ अंशांचा कोन करून परावर्तित झालेल्या इलेक्ट्रॉनांचा अभ्यास केला जातो. या सर्व पद्धतीत अखेरीस इलेक्ट्रॉन छायाचित्रण काचेवर पडतात व त्यावर विशिष्ट विवर्तन आकार उमटतो. अशा प्रयोगात उच्च निर्वात अवश्य आहे, नाहीतर शलाकेच्या मार्गातील हवेच्या रेणूंमुळेही प्रकीर्णन होऊ शकेल. झोतरूपाने आत सोडलेला वायूही शक्य तितक्या लौकर बाहेर काढून घेणे अवश्य असते. विवर्तन छायाचित्रावरून पदार्थातील अणूंच्या स्थानासंबंधी संपूर्ण माहिती मिळते किंवा पदार्थाची रासायनिक माहिती मिळते. घन पृष्ठावरील पातळ पटलांचा अभ्यास करणे इलेक्ट्रॉन विवर्तनामुळे शक्य झाले आहे. वंगणक्रिया तसेच तरंगण्याच्या धर्मामुळे होऊ शकणारे खनिजांचे विश्लेषण यांमध्ये या पटलांचे फार महत्त्व आहे [→ इलेक्ट्रॉन विवर्तन].
इलेक्ट्रॉन भिंग व इलेक्ट्रॉन आरसा : बहिर्गोल भिंग वापरून ज्याप्रमाणे दृश्य प्रकाशाचे संकेंद्रीकरण होऊ शकते त्याप्रमाणे विद्युत् क्षेत्र अगर कर्षुकीय क्षेत्र वापरूनइलेक्ट्रॉन शलाकेचे संकेंद्रीकरण करता येते. तसेच विद्युत् क्षेत्र वापरून आरशामुळे ज्याप्रमाणे दृश्य प्रकाशाचे परावर्तन होते, त्याप्रमाणे इलेक्ट्रॉन शलाकेचे परावर्तनही साधता येते. अशा भिंगांची अथवा आरशांची योजना इलेक्ट्रॉन सूक्ष्मदर्शकामध्ये केली जाते. इलेक्ट्रॉन सूक्ष्मदर्शक हे एक प्रभावी साधन असून त्याची विभेदनक्षमता (पृथक्करण करण्याची क्षमता) प्रकाशीय सूक्ष्मदर्शकापेक्षा पुष्कळच उच्च दर्जाची आहे. गोलीय विक्षेप (एक प्रकारचा दोष)टाळण्यासाठी सु. ०·५ × १०-३ सेंमी. व्यासाचे रंध्र ठेवल्यास व ०·५ A० या तरंगलांबीचे इलेक्ट्रॉन वापरल्यास या सूक्ष्मदर्शकाची विभेदनक्षमता सु. १० A० इतकी येते.
रेडिओच्या प्रसारामुळे इलेक्ट्रॉन नलिका सर्वांस माहीत आहेतच. अशी नलिका निर्वात असून तप्त ऋणाग्रापासून मुक्त इलेक्ट्रॉन बाहेर पडतात व समोर थोड्या अंतरावर असलेल्या पट्टीच्या आकाराच्या धन अग्राकडे ते आकर्षित झाल्याने एकदिश विद्युत् प्रवाह मिळतो. प्रवाहाच्या नियंत्रणासाठी जालकाची (जाळीसारख्या विद्युत् अग्राची) योजना असते. अग्रांच्या संख्येप्रमाणे या नलिकांस द्विप्रस्थ (डायोड), त्रिप्रस्थ (ट्रायोड), पंचप्रस्थ (पेंटोड) इ. नावे आहेत. ऋण किरण दोलनदर्शक ही इलेक्ट्रॉन नलिकाच असून, तीत तिच्या एका टोकास असलेल्या लहान पडद्यावर इलेक्ट्रॉन शलाकेचे संकेंद्रीकरण होते व त्या जागी पडदा प्रकाशित होतो. पडद्यावर विशिष्ट वक्र (ध्वनिविश्लेषणाच्या संदर्भात) अथवा एखादे दृश्य (दूरचित्रवाणीच्या संदर्भात) दिसते.
इलेक्ट्रॉन नलिकेत निर्वाताऐवजी अत्यंत कमी दाबाच्या वायूने अगर बाष्पाने ती भरून तिच्या ऋण व धन अग्रांमध्ये जरूर ते विद्युत् वर्चस् ठेवल्यास, त्या त्या वायूचा अगर बाष्पाचा लाक्षणिक प्रकाश मिळतो. वर्णपट विश्लेषणासाठी अशा तऱ्हेच्या नलिका प्रकाश उद्गम म्हणून वापरतात.
पहा : अणु व आणवीय संरचना; इलेक्ट्रॉन सूक्ष्मदर्शक; इलेक्ट्रॉनीय मापन; इलेक्ट्रॉनीय प्रयुक्ति.
संदर्भ : 1. Crowther, J. A. Ions, Electrons and Ionising Radiations, London, 1949.
2. Hoag, J. B.; Korff, S. A. Electrons and Nuclear physics, London, 1948.
3. Millikan, R. A., The Electrons (+ and – ), Protons, Photons, Neutrons and Cosmic Rays, Chicago, 1947.
भावे, श्री. द.