खगोलीय यामिकी

खगोलीय यामिकी : सूर्यमालेतील ग्रह, उपग्रह, लघुग्रह (मंगळ व गुरू यांच्या कक्षांच्या मधल्या पट्ट्यातील छोटे छोटे ग्रह), धूमकेतू इत्यादींचे सूर्याभोवतालचे भ्रमण समजून घेऊन आकाशात ते केव्हा व कोठे दिसतील हे वर्तविणे हेच खगोलीय यामिकीचे मुख्य कार्य आहे (यामिकी म्हणजे प्रेरणांची वस्तूंवर होणारी क्रिया आणि त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणारे शास्त्र). या विषयाची सुरुवात फार प्राचीन काळी झालेली असली, तरी तिला आधुनिक शास्त्रीय स्वरूप न्यूटन यांच्या गुरुत्वाकर्षणविषयक सिद्धांतानंतरच मिळाले. कृत्रिम उपग्रह व अंतरिक्ष प्रवास यांच्यासारख्या अत्याधुनिक समस्यांमध्ये या ज्ञानशाखेचा फार उपयोग होतो. त्यामुळे तिला नवीनच महत्त्व प्राप्त झाले आहे.

ग्रहमालेसंबंधीची भूकेंद्रीय कल्पना इसवी सनाच्या दुसऱ्या शतकात टॉलेमी यांनी सुस्थिर केली व पुढे सु. १,४०० वर्षांपर्यंत ज्योतिर्विद तिचा उपयोग करीत होते. परंतु त्या कल्पनेनुसार वर्तविलेल्या ग्रहस्थिती, प्रत्यक्ष घेतलेल्या त्या त्या ग्रहाच्या वेधांशी तुलना करता, बऱ्याच चुकीच्या आहेत असे दिसून येई. त्यामुळे सोळाव्या शतकात कोपर्निकस यांनी सूर्यकेंद्रीय कल्पना पुढे आणली आणि तिला गणिती रूप दिले.

सूर्यकेंद्रीय पद्धतीच्या मदतीने गणितकृत्ये जास्त सोपी झाली प्रतियोग (पृथ्वी व सूर्य यांना जोडणाऱ्या रेषेत पण पृथ्वीच्या विरुद्ध बाजूस असण्याच्या) अवस्थेत मंगळ, गुरू, शनी यांसारखे बाह्यग्रह वक्री (पृथ्वीच्या गतीमुळे ताऱ्यांमध्ये ग्रहांची नेहमीच्या विरुद्ध म्हणजे पूर्वेकडून पश्चिमेकडे होणारी भासमान गती) का होतात, तसेच बुध व शुक्र हे अंतर्ग्रह सूर्यापासून फार दूर का जाऊ शकत नाहीत याचे स्पष्टीकरण देता आले इतकेच नव्हे, तर सर्व ग्रहांची सापेक्ष अंतरेही निश्चित करता आली. त्यामुळे सूर्यकेंद्रीय पद्धती शेवटी सर्वमान्य झाली.

सूर्यकेंद्रीय पद्धतीच बरोबर असल्याची आणखी काही प्रमाणे नंतर मिळाली ती अशी : (१) या पद्धतीनुसार शुक्र व बुध या अंतर्ग्रहांना चंद्राप्रमाणे कला असाव्या असे अनुमान निघाले. शुक्राच्या कलांचे इ. स. १६१० नंतर दुर्बिणीच्या साहाय्याने गॅलिलीओ यांनी प्रत्यक्ष अवलोकन केले. (२) इ. स. १८५१ मध्ये फूको यांनी पॅरिसमध्ये केलेल्या लंबकाच्या प्रयोगावरून पृथ्वीच्या परिवलनाचा (स्वत:च्या अक्षाभोवती फिरण्याचा) प्रत्यक्ष पुरावा मिळाला. (३) पृथ्वीच्या सूर्याभोवतलाच्या भ्रमणामुळे निर्माण होणारी ताऱ्यांची लंबनिक (निरीक्षकाच्या स्थानांत बदल झाल्यामुळे होणारी भासमान) गती आणि त्यांच्या दिशेतील प्रकाशीय विपथन (प्रकाशाचा वेग व निरीक्षकाचा वेगयांच्या संयोगामुळे ताऱ्याच्या स्थानात होणारा भासमान बदल) तसेच त्यांच्या दृष्टिरेषेतील भासमान गतीमधील आवर्ती (नियतकालिक) बदल या गोष्टी अनुभवास आल्या.

केप्लर यांचे नियम : डेन्मार्कमधील ट्यूको ब्राए यांनी ग्रहाचे इतके अचूक वेध घेतले की, त्यांनी निश्चित केलेल्या ग्रहांच्या स्थानांत १´ पेक्षा जास्त चूक शक्य नव्हती. परंतु याच्याशी तुलना करता कोपर्निकस यांच्या पद्धतीने गणितकृत्ये करून काढलेल्या ग्रहांच्या स्थानात ३-४ अंशांची तफावत पडते, असे दिसून आले. त्यामुळे कोपर्निकस यांच्या पद्धतीत काही सुधारणा करणे जरूर वाटू लागले.सतराव्या शतकाच्या सुरुवातीस केप्लर यांनी टॉलेमी यांच्यापासून रूढ असलेल्या वर्तुळाकार कक्षांचा त्याग करून त्या कक्षा विवृत्ताकार (लंबवर्तुळाकर) असल्या पाहिजेत, हा विचार मांडला आणि ‘केप्लर यांचे नियम’ नावाने प्रसिद्ध असलेले ग्रहांच्या गतीने पुढील तीन नियम मांडले. या कामी त्यांना ब्राए यांच्या सूक्ष्मवेधांचा फारच उपयोग झाला.

पहिला नियम : सर्व ग्रह सूर्याभोवती विवृत्ताकार परिभ्रमण-कक्षांत फिरतात (आ.१) व विवृत्ताच्या दोन केंद्रांपैकी एकावर सूर्य असतो.

दुसरा नियम : ग्रहपरिभ्रमण-कक्षेत कोठेही असला, तरी त्याला व सूर्याला जोडणारी केंद्ररेषासारख्या वेळात सारखेच क्षेत्रफळ कापते. उदा., आ. १ मध्ये E, S, F व G, S, H या विवृत्त खंडाचे क्षेत्रफळ सारखेच असल्याने ग्रहाला E पासून F पर्यंत जाण्याला जो वेळ लागतो तेवढाच वेळ त्याला G पासून H पर्यंत जाण्यास लागतो म्हणजे ग्रह सूर्याच्या जवळजवळ येतो तसतसा त्याचा वेग वाढत जातो.

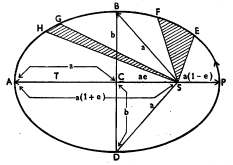
तिसरा नियम : ग्रहाच्या परिभ्रमण कालाचा वर्ग त्याच्या कक्षेच्या दीर्घ-अक्षार्धाच्या घनाच्या सम प्रमाणात असतो. म्हणजेच ग्रहाच्या कक्षेच्या दीर्घ अक्षाचीलांबी 2a व भ्रमण काल T असेल, तर T² α a³ विवृत्ताच्या दीर्घ-अक्षाची लांबी AP = 2a आणि लघु-अक्षाची लांबी BD=2b असेल (आ.१), तर

ग्रहाचे सूर्यापासूनचे अंतर, ग्रह P या उपसूर्य बिंदूवर (ग्रहाच्या कक्षेतील सूर्यापासून सर्वांत जवळच्या बिंदूवर) असताना कमीतकमी, म्हणजे SP = a (l – e) असते तर ग्रह A या अपसूर्य बिंदूवर(ग्रहांच्या कक्षेतील सूर्यापासून सर्वांत दूरच्या बिंदूवर) असताना त्याचे सूर्यापासूनच अंतर SA = a (l + e), म्हणजे जास्तीतजास्त असते. म्हणजे दीर्घ-अक्षाचा अर्ध a हे माध्य अंतर झाले. पृथ्वीचे सूर्यापासूनचे माध्यअंतर १·४९६ × १०^८ किमी. असून त्याला खगोलशास्त्रीय एकक असे म्हणतात. खगोलीय अंतरे सामान्यत: या एककात सांगतात.

केप्लर यांच्या नियमानुसार काढलेल्या ग्रहस्थिती, आकाशात दिसणाऱ्या त्यांच्या स्थितीशी फारच चांगल्या जुळू लागल्या. त्यामुळे सूर्यच ग्रहमालेच्या केंद्रस्थानी आहे या कल्पनेलापुष्टी मिळाली. पुढे न्यूटन यांनी केप्लर यांच्या नियमांना सैद्धांतिक बैठकदिली.

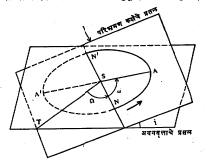
एखाद्या ग्रहाची विशिष्ट वेळेची स्थिती निश्चित करण्यासाठी एकूण सातमूलके माहीत असणे आवश्यक असते. त्यांपैकी कक्षेचा व्याप व आकार निश्चितकरणाऱ्या (१) दीर्घ अक्षाचा अर्थ a आणि (२) विमध्यता e यांचा विचार वर आलेलाच आहे. ग्रहाची कक्षापातळी पृथ्वीच्या कक्षापातळीला, ज्या दोन बिंदूंतछेदते (N व N´, आ. २) त्यांना पात असे म्हणतात. त्यांपैकी N या पातबिंदूच्या ठिकाणी पृथ्वीच्या कक्षापातळीला छेदताना ग्रह पातळीच्या दक्षिणेकडून उत्तरेकडे जात असतो. त्या पातबिंदूला ऊर्ध्वपात व N´ ला अधोपात असेम्हणतात. (३) पृथ्वीची कक्षापातळी व ग्रहाची कक्षापातळी यांच्यामधीलतिर्यक् कोन i (४)  वसंत संपात Ý व ग्रहाचा ऊर्ध्वपात N यांनी सूर्याचे ठायी अंतरित केलेला कोन Ω हा कोन अयनवृत्ताच्या (पृथ्वीच्या कक्षापातळीने खगोलात छेदल्याने मिळणाऱ्या वर्तुळाच्या) पातळीत असतो. (५) ऊर्ध्वपातापासून ग्रहाच्या नीच स्थानापर्यंत (A) ग्रहाच्या कक्षापातळीत मोजलेला कोन ω, (६) ग्रह नीच स्थानावर येण्याचा काल Tω आणि (७) ग्रहाचानाक्षत्रीय परिभ्रमण काल T, ही ती सात मूलके होत [→ कक्षा].

न्यूटन यांचा गुरुत्वाकर्षणाचा सिद्धांत :गतिविषयकतीन नियम प्रथम न्यूटन यांनी स्पष्ट स्वरूपात मांडले. त्यांना न्यूटनयांचे गतिविषयक नियम म्हणतात. त्याच्या आधी गॅलिलीओ यांनाही त्या नियमांची कल्पना आलेली होती.

एखादा ग्रह ज्या अर्थी विवृत्ताकार कक्षेत विषम गतीने फिरतो त्या अर्थी न्यूटन यांच्या पहिल्या गतिविषयक नियमानुसार त्या ग्रहावर बाह्य प्रेरणा लागू होत असलीच पाहिजे. तसेच केप्लर यांच्या नियमांचा विचार करता ह्या प्रेरणेचा सूर्याशी संबंध असला पाहिजे, असा निष्कर्ष निघतो. चंद्र आणि पृथ्वी यांचा अन्योन्य संबंध हा ग्रह- सूर्यसंबंधासारखाच आहे म्हणून असाच निष्कर्ष चंद्राच्या बाबतीतही काढता येईल.केप्लर यांच्या नियमावरून न्यूटन यांना गुरुत्वाकर्षणाचा सार्वत्रिक सिद्धांत सुचला त्यानुसार कोणत्याही दोन वस्तुकणांतील गुरुत्वाकर्षणची प्रेरणा F ही त्यांच्यामधील अंतर d च्या वर्गाच्या व्यस्त प्रमाणात ववस्तुमानांच्या (M व m  यांच्या) गुणाकाराच्या सम प्रमाणात असते

मूल्य ६·६७ x १०^-८ सेंमी. ^३/ ग्रॅ.से.^२ असे आहे.

गुरुत्वाकर्षणाच्या नियमाचाउपयोग : सूर्य किंवा ग्रह-उपग्रह असंख्य कणांचे बनलेले असले, तरी त्यांच्या गोलीय सममितीमुळे (समरूपतेमुळे) त्यांचे सर्वच्या सर्व वस्तुमानत्यांच्या मध्याशीच स्थित (एकवटलेले) आहे असे मानून त्यांचे दूर अंतरावर होणारे आकर्षण काढता येते. त्याचप्रमाणे सूर्याचे वस्तुमान सर्व ग्रहांच्या संयुक्त वस्तुमानाच्या एक हजार पट इतके प्रचंड असल्यामुळे कोणत्याही ग्रहाच्या गतीचा विचार करताना त्यावर केवळ सूर्याचेच आकर्षण लागू होते असे मानले, तरी फारशी चूक होत नाही. हाच न्याय ग्रह व त्याचा उपग्रह यांच्या बाबतीत लागू होतो. या दोन गोष्टींमुळे ग्रहांच्या गतीची गणितकृत्ये फारच सोपी होतात व गुरुत्वाकर्षणाच्या नियमावरून केप्लर यांचे नियम सिद्ध करता येतात, एवढेच नाही तर त्या नियमांत काही सुधारणाही करता येतात.

ग्रहांच्या गती व्यस्तवर्गीय (अंतराच्या वर्गाच्या व्यस्त प्रमाणातील) आकर्षणाखाली होत असतील, तर ग्रहांच्या परिभ्रमण कक्षा विवृत्ताखेरीज ⇨अन्वस्त (पॅराबोला) व ⇨अपास्त (हायपरबोला) या आकारांच्याही होऊ शकतील. पण अशा कक्षेतील पदार्थ सूर्यापासून कायमचा दूर जाईल. सूर्यमालेत अशा कक्षा दुर्मिळ आहेत.

न्यूटन यांच्या सिद्धांतानुसार, केप्लर यांच्या तिसऱ्या नियमाऐवजी

ग्रहांची वस्तुमाने भिन्नभिन्न असल्याने T² α a³ हा सोपा नियम संपूर्णपणे लागू पडत नाही, परंतु M च्या मानाने m फारचलहान असल्याने आसन्नतेचे (अंदाजाने)

जोडीलाही लागू पडतो. म्हणून a व T माहीत असल्या सत्यावरून ग्रहाचे वस्तुमान काढता येते (पहा: कोष्टक).

इतर निष्कर्ष :(१) न्यूटन यांच्या गतिविषयक तिसऱ्या नियमानुसार जेवढ्या प्रेरणेने सूर्य एखाद्या ग्रहाला आपल्याकडे खेचतो तेवढ्याच प्रेरणेने ग्रहही सूर्याला स्वत:कडे खेचीत असतो. त्यामुळे दोघेही त्यांच्या उभय-वस्तुमान मध्याभोवती भ्रमण करतात. हीच गोष्ट पृथ्वी आणि चंद्र या जोडीलाही लागू पडते. परंतु सूर्याचे वस्तुमान ग्रहाच्या मानाने फार प्रचंड असते त्यामुळे सूर्याची भ्रमणगती दुर्लक्षणीय असते. पृथ्वी व चंद्र यांचे वस्तुमान ८१·३ : १ याप्रमाणात आहे. त्यामुळे त्यांचा उभय-वस्तुमान मध्ये पृथ्वीच्या मध्यापासून सु. ४,७५० किमी. अंतरावर आहे व त्याभोवती होणाऱ्या पृथ्वीच्या भ्रमणामुळे सूर्य दर महिन्यात ६.६´´ मागेपुढे झालेला दिसतो.

(२) ग्रहांप्रमाणेच धूमकेतूही सूर्याच्या भोवती भ्रमण करत असतात, असे न्यूटन यांनी दाखवून दिले. पुढे हॅली यांनी २४ धूमकेतूंच्या कक्षा निश्चित केल्या, तेव्हा असेदिसून आले की, इ.स. १५३१, १६०७ व १६८२ मध्ये दिसलेल्या धूमकेतूंच्या कक्षा एकसारख्याच आहेत. तेव्हा हे वेगवेगळे तीन धूमकेतू नसून एकच धूमकेतू ७५-७६ वर्षांनी पुन:पुन्हा दिसत असला पाहिजे, असा निष्कर्ष त्यांनी काढला. हाहॅली यांचा धूमकेतू पुढे १७५८-५९ मध्ये व त्यानंतर प्रत्येक वेळीसूर्याच्या जवळ आला म्हणजे दिसत आलेला आहे.

(३) इ.स. १८०१ पासूनआतापर्यंत ज्ञात झालेले सर्व १६५० लघुग्रहसुद्धा गुरुत्वाकर्षणामुळे सूर्याभोवती भ्रमण करतात असे आढळून आले आहे. त्यांच्या कक्षा बहुधा मंगळ व गुरू यांच्या कक्षांच्या दरम्यान आढळतात (पहा: कोष्टक).

बहुपिंड व्यूहाचाविचार : सूर्यमालेत सूर्याशिवाय अनेक ग्रह, उपग्रह इ. आहेत. त्यांपैकी कोणत्याही एकावर बाकीच्या सर्वांचे गुरुत्वाकर्षण लागू होत असते, ही गोष्ट लक्षात घेऊन प्रत्येकाच्या गतिस्थितीचा अभ्यास करण्यासाठी बहुपिंड (अनेक वस्तूंच्या) व्यूहाचा विचार करणे आवश्यक झाले. हे कार्य अठराव्या व एकोणिसाव्या शतकांत क्लेरो, ॲलांबेर, ऑयलर, लाग्रांझ, लाप्लास, गौस, हिल, प्वँकारे इ. महान गणितज्ञांनी केले. त्यांच्या कार्याचा थोडक्यात आढावा खाली घेतला आहे.

(अ) ग्रहांच्या गतीतीलविक्षोभ : एखाद्या ग्रहावर फक्त सूर्याचेच गुरुत्वाकर्षण होत असल्यास त्या ग्रहाची एकविशिष्ट विवृत्ताकार कक्षेतील गती निष्पन्न होईल. या गतीत इतर ग्रहवगैरेंच्या आकर्षणामुळे होणाऱ्या परिवर्तनास विक्षोभ (क्षुब्धता) असे म्हणतात. सूर्याच्या मानाने या इतर ग्रह वगैरे पदार्थांचे आकर्षण अगदीच दुर्बल असल्याने हा विक्षोभ पायरी पायरीने विचारात घेता येतो. या तत्त्वावर आधारलेल्या अशा विक्षोभाच्या दोन पद्धती आहेत.

(१) विशिष्ट विक्षोभपद्धती : या पद्धतीत ग्रहाच्या अविक्षोभित कक्षेचा विचान न करता, ग्रहाच्या गति-समीकरणात विक्षोभ करणाऱ्या सर्व प्रेरणांचा समावेश करतात व त्या समीकरणावरून ग्रहस्थिती काढतात. या पद्धतीने १००-२०० वर्षांपर्यंतही ग्रहस्थिती पुष्कळशी अचूक काढता येते. हिचा उपयोग पंचांगे तयार करण्यासाठी करतात. परंतु त्यानंतर गणनक्रियेतील चुका वाढत जातात व त्या सुधारण्यासाठी स्पष्ट ग्रहांच्या नवीन वेधांची आवश्यकता लागते.

धूमकेतू व लघुग्रह यांची गतिस्थिती वर्तविताना, गुरू व शनी यांच्या आकर्षणाचे परिणाम लक्षात घेण्यासाठीही या पद्धतीचा उपयोग होतो. या पद्धतीचा उपयोग उलट बाजूने करून नेपच्यून व प्लूटो या ग्रहांचे शोध लावता आले.

इ.स. १७८१ मध्ये हर्शेल यांना युरेनस या शनीच्या पलीकडील ग्रहाचा शोध लागला. १८४४ मध्ये या ग्रहाच्या स्थितीत२´ ची चूक येऊ लागली. तिच्या मुळाशी एखाद्या अज्ञात ग्रहामुळे होणारा विक्षोभ असला पाहिजे असा अंदाज करून ॲडम्स व लव्हेऱ्ये यांनी (स्वतंत्रपणे) या अज्ञात ग्रहाची संभाव्य कक्षा निश्चित केली. त्यानुसार वेध घेऊन १८४६ मध्ये बर्लिन वेधशाळेतील गॉल यांनी दुर्बिणीच्या साहाय्याने नेपच्यून ग्रह हुडकून काढला. अशाच पद्धतीने पुढे प्लूटो या दूरतम ग्रहाचाही शोध लावला.

(२) सर्वसाधारण विक्षोभपद्धती : या पद्धतीत एखाद्या ग्रहाच्या विशिष्ट वेळच्या ग्रहस्थितीचा विचार न करता, इतर ग्रहांच्या आकर्षणामुळे त्या ग्रहाच्या कक्षेच्या मूलकांचा विक्षोभ अजमावला जातो. या पद्धतीच्या उपयोगाने ग्रहांच्या कक्षांत होणारे आवर्तीबदल तसेच सूर्यमालेच्या अतिप्राचीन व दीर्घभविष्यकालिक स्थिती वर्तविता येतात. उदा., गुरूच्या आकर्षणामुळे पृथ्वीच्या कक्षेत १ व १२ वर्षांच्या आवर्तकालाचे बदल होतात. त्यांना लघु-आवर्तकालिक विक्षोभ म्हणतात. तसेच गुरू व शनी यांच्यामधील परस्पर आकर्षणामुळे त्यांच्या कक्षांत ९०० वर्षांच्या आवर्तकालाचे बदल होतात. अशा परिवर्तनांना दीर्घ-आवर्तकालिक विक्षोभ म्हणतात. विक्षोभ आवर्ती नसल्यास त्यांना आवर्तहीन विक्षोभ म्हणतात. अशा विक्षोभामुळे सूर्यमालेतील ग्रह बाहेर फेकले जाऊ शकतील. परंतु याप्रकारचे विध्वंसक विक्षोभ सूर्यमालेत होत नाहीत. असे दिसून आले आहे की, आवर्तहीन वाटणारे बहुतेक सर्व विक्षोभ वस्तुत: अतिदीर्घ-आवर्तकालिक असतात. एकंदरीत आपली सूर्यमाला बव्हंशी चिरस्थायी, असे म्हणावयास हरकत नाही.

(आ) त्रिपिंड व्यूहाचाविचार : बहुपिंडव्यूहाची समस्या फारच जटिल असल्याने त्याहून तुलनेने सोप्या अशा त्रिपिंड आणि चतुष्पिंड व्यूहांचा जास्त विचार झाला व त्यापासून आवर्तकक्षा असलेले बरचे निर्वाह (गति-समीकरणे सोडवून मिळणारी उत्तरे) मिळाले. परंतु हेही प्रश्न कठीण असून अलीकडे ते इलेक्ट्रॉनीय संगणकाच्या (गणितीय कृत्ये करणाऱ्या यंत्राच्या) साहाय्याने सोडविण्याचा प्रयत्न होऊ लागला आहे. १९१२ मध्ये के. एफ्. संडमान यांनी त्रिपिंड प्रश्नाचा सर्व काल मूल्यांकरिता विस्तार करता येणाऱ्या अभिसारी घात श्रेणीच्या स्वरूपातील निर्वाह मिळविला. प्वँकारे व बर्‌कॉफ यांनीही यांसंबंधी महत्त्वाचे कार्य केले आहे.

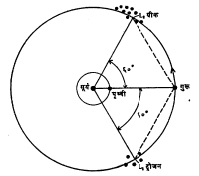त्रिपिंडांपैकी एकाचे वस्तुमान अत्यंत कमी असल्यास त्याचे बाकीच्या दोन पदार्थांवरील आकर्षण दुर्लक्षणीय मानून हा प्रश्न सोडविता येतो. याला मर्यादित त्रिपिंड प्रश्न असे म्हणतात. यातील दोन मोठ्या पदार्थांची गतिस्थिती द्विपिंड व्यूहाप्रमाणेच असेल असे मानून केवळ तिसऱ्या लघुपिंडाची गतिस्थिती निश्चित केली जाते. मोठ्या दोन पदार्थांची गती त्यांच्या वस्तुमान मध्याभोवती वर्तुळाकार आहे असे मानल्यास तिसरा लघुपिंड त्याच्या कक्षापातळीत समभुज त्रिकोण साधणाऱ्याL₁, L₂ या बिंदूंवर समतोल स्थितीत राहू शकेल असे लाग्रांझ यांनी दाखवून दिले (आ.३). उदा., सूर्य व गुरू हे दोन मोठे पिंड मानून मिळणाऱ्याL₁ व L₂ या बिंदूंजवळ ट्रोजन व ग्रीक ग्रह या नावाने ओळखले जाणारे काही लघुग्रह सापडतात.

उपग्रहांची गतिस्थिती : (अ) पृथ्वीच्या चंद्राप्रमाणे इतर ग्रहांनाही उपग्रह आहेत. उदा., गुरूला बारा तर शनीला नऊ उपग्रह आहेत. हे दोन मोठे ग्रह व त्यांचे उपग्रह म्हणजे सूर्यमालेच्या छोट्या प्रतिकृतीच असल्याने त्यांच्या उपग्रहांना सूर्यमालेचीच यामिकी लावता येते. या उपग्रहांच्या बाबतीत विक्षोभाचे आणखी एक कारण असे आहे : बहुतेक ग्रह (त्यांच्या परिवलनामुळे) ध्रुवांजवळ चपटे व विषृववृत्ताजवळ फुगीर झालेले असतात. म्हणून त्यांच्यापासून फार दूर नसलेल्या उपग्रहांवर होणारे त्यांचे आकर्षण बरोबर व्यस्तवर्गीय स्वरूपाचे नसते त्यामुळे उपग्रहाची कक्षा अवकाशात स्थिर न राहता ग्रहाच्या अक्षाभोवती ग्रहाच्या भ्रमण दिशेच्या उलट दिशेने प्रदक्षिणा करते व कक्षेचे पात पाठीमागे सरकत जातात. हा परिणाम पृथ्वीभोवती फिरणाऱ्या कृत्रिम उपग्रहांच्या बाबतीतही अनुभवाला येतो आणि त्याच्यावरून पृथ्वीचा आकार अधिक अचूकपणे अजमावण्यात आला आहे.

आपल्या चंद्राच्या गतीत सूर्यामुळे होणारा विक्षोभ विशेष महत्त्वाचा आहे. पृथ्वीच्या ध्रुवांजवळचा चपटेपणा, च्रंद्राचा विशिष्ट आकार, त्याचप्रमाणे इतर ग्रहांची आकर्षणे यांमुळेही काही फरक पडतात. चंद्राच्या गतीतील मुख्य विकार पुढीलप्रमाणे आहेत : वार्षिक असममिती, चांद्रपातांचे (राहू-केतूचे) प्रतिगामी चलन, तिर्यक् कोनाचा आवर्ती बदल. दीर्घ अक्षाची पुरोगामी प्रदक्षिणा, अपभूस्थानाची (चंद्राच्या कक्षेतील पृथ्वीपासून सर्वांत दूरच्या स्थानाची) व पातांची असममिती. यांपैकी पातांच्या प्रतिगामी चलनाचा आवर्तकाल १८·६ वर्षे असल्याने अमावास्या (आवर्तकाल २९·५३ दिवस), चंद्र-राहू युती (आवर्तकाल २७·२१ दिवस), सूर्य-राहू युती (आवर्तकाल ३४६·६ दिवस) या तिन्ही गोष्टी १८ वर्षे ११·३३ दिवस इतक्या अवधीने पुन्हा एकत्र येतात. हाच ग्रहणचक्राचा ‘सारोस’ काल होय[→ ग्रहण].

(आ) पृथ्वीच्या परिवलनावर होणारा चंद्र-सूर्याचा परिणाम पृथ्वी आपल्या अक्षाभेवती २३ तास ५६ मिनिटे ४·०९० सेकंद या काळात एक प्रदक्षिणा पूर्ण करते. तिच्या या परिवलन गतीमुळे तीध्रुवावर चपटी आणि विषृववृत्तावर फुगीर झाली आहे. पृथ्वीचे विषुववृत्त तिच्या परिभ्रमण कक्षापातळीशी २३.५ अंशांचा कोन करते. चंद्रसूर्याचे आकर्षण विषुववृत्ताला कक्षापातळीत आणण्याचा प्रयत्न करते. परंतु पृथ्वीच्या घूर्णीय (स्वत:भोवती फिरण्याच्या) परिणामामुळे याला विरोध होतो व परिणामी परांचनामुळे (ज्या अक्षाभोवती वस्तू फिरते त्या अक्षाच्या फिरण्यामुळे) पृथ्वीचे अक्ष-ध्रृव कक्षा-ध्रृवाभोवती उलट्या दिशेने प्रदक्षिणा करतात. त्यामुळे वसंतसंपात कक्षावृत्तावरून मागे मागे सरकत जातो. याला संपातचलन असे म्हणतात. यामुळे वसंतसंपात अश्विनी → रेवती → पूर्वाभाद्रपदा असा मागे सरकत जातो. ही संपात गती प्रतिवर्षी ५०·२६´´ असल्याने संपाताला एक प्रदक्षिणा पूर्ण करण्यास २५,८०० वर्षे लागतात. या मोठ्या प्रदक्षिणेवर १९ वर्षे आवर्तकालाचे एक छोटे आंदोलन अध्यारोपित आहे. याला ⇨अक्षांदोलन असे म्हणतात. चंद्राची कक्षा पृथ्वीच्या कक्षेशी सु. ५ अंशांचा कोन करते व चंद्राचे पात १८·६ वर्षांत उलटी प्रदक्षिणा पूर्ण करतात. यामुळे चंद्राच्या आकर्षणात होणारा बदल हे अक्षांदोलनाचे कारण आहे.

समुद्राला येणारी भरती-ओहोटी हा चंद्र-सूर्याच्या आकर्षणाचा दुसरा महत्त्वाचा परिणाम आहे. समुद्रावरील चंद्राचे आकर्षण सूर्यापेक्षा दुप्पट जोरदार असल्याने चंद्राच्या उदय व अस्तावर भरती जास्त अवलंबून राहते. चंद्राबरोबर जसजशी भरतीची लाट पुढे सरकते तसतसे त्या पाण्याच्या घर्षणामुळे पृथ्वीचे अक्षभ्रमण अतिसूक्ष्म प्रमाणात मंदावते. त्यामुळे दिवस दर शंभर वर्षांत ०·००१ सेकंदाने मोठा होतआहे. त्याचबरोबर कोनीय संवेगाच्या (निरूढी परिबल x कोनीय वेग या गुणाकाराच्या, निरूढी परिबल म्हणजे एखाद्या अक्षाभोवती फिरणाऱ्या) वस्तूच्या कोनीय प्रवेगास होणाऱ्या त्या वस्तूच्या विरोधाचे माप) अक्षय्यत्वाच्या सिद्धांतानुसार चंद्र पृथ्वीपासून हळूहळू दूर जात आहे. या गोष्टीचे दूरगामी परिणाम जॉर्ज हौअर्ड डार्विन (१८४५-१९१२) या गणितज्ञांनी विचारात घेतले व त्यावरून पृथ्वी-चंद्र या जोडीचा पूर्वेतिहास व भविष्यकालीन रचना यांबद्दल काही तर्क बांधले.

सापेक्षतेचा सिद्धांत : न्यूटन यांच्या गुरुत्वाकर्षणाच्या सिद्धांतावरून सूर्यमालेतील कोणत्याही ग्रहादिकांची स्थिती अत्यंत सूक्ष्मतेने काढता येऊ लागली. परंतु बुध ग्रहाच्या बाबतीत एक महत्त्वाचा अपवाद येत असे. बुधाचे उपसूर्य स्थान शंभर वर्षांत सु. ४३´´ पुढे सरकते ही वेध्रसिद्ध गोष्ट आहे. सर्व प्रकारच्या विक्षोभ क्रिया विचारात घेऊनही याची काहीच उपपत्ती करता येत नव्हती. परंतु आइन्स्टाइन यांच्या व्यापक सापेक्षता सिद्धांतावरून याचा उलगडा झाला. त्यावरून न्यूटन यांचे गती व गुरुत्वाकर्षण यांसंबंधीचे नियमआसन्न स्वरूपाचेच आहेत असे दिसून आले [→ सापेक्षता सिद्धांत].

तारकीय गतिकी : आकाशात शेकडो तारका-युगुले त्यांच्या परस्पर वस्तुमान-मध्याभोवती फिरत आहेत. त्यांची ही गती गुरुत्वाकर्षणाच्या सिद्धांताला धरूनच होते, हे पूर्वीपासून माहीत झाले होते. विसाव्या शतकात याच सिद्धांताचा उपयोग आकाशगंगेतील ताऱ्यांचे भ्रमण स्पष्ट करण्यासाठी झाला. हे सर्व तारे आकाशगंगेच्या मध्याभोवती गुरुत्वाकर्षणाच्या नियमानुसारच फिरतात आणित्यांच्या गतीवरून आकाशगंगेचे वस्तुमान ठरविता येते. तसेच बहुपिंडव्यूहाच्या कल्पनेचा उपयोग करून तारकासमूहांचे वस्तुमान आणि कालमान अजमावता येते.

संपूर्ण विश्वाचे प्रसरणही गुरुत्वाकर्षणामुळे मंदावले जात आहे. यासाठी विश्वातील पदार्थाची सरासरी घनता काही विशिष्ट मर्यादेपेक्षा जास्त असली पाहिजे, यावरून वस्तुमान अंदाज बांधता येतो.

संदर्भ : 1. Danby, J. M. A. Fundamentals of Celestial Mechanics, New York, 1962.

2. Finley-Freundlich, E. Celestial Mechnics, London, 1958.

3. McCuskey, S. W. Introduction to Celestial Mechanics, Reading, Mass, 1963

4. Moulton, F. R. Introduction to Celestial Mechanics, 1914.

अभ्यंकर, कृ. दा.