गोटी चौकट : (अबॅकस). गोटीचौकटीचा उपयोग पूर्णांक व त्यांची बेरीज (वा वजाबाकी) या प्राथमिक गणितकृत्याविषयीची कल्पना सुलभपणे समजावून देण्याकरिता होतो. एका चौकटीवर समांतर अशा तीन अगर अधिक आडव्या तारा बसवून त्या प्रत्येकींमध्ये दहा दहा गोट्या किंवा मणी ओवलेले असतात. सर्वांत खालची तार एकं स्थान, त्यावरील तारा अनुक्रमे दहं, शतं इ. स्थाने दाखवितात. सर्व मणी प्रथम डाव्या बाजूस ठेवतात आणि जी संख्या दाखवावयाची असेल तीनुसार हवे तितके मणी उजवीकडे सरकवितात. उदा., ४३२ ही संख्या दाखवावयाची असेल तर एकं, दहं आणि शतंच्या तारांवर अनुक्रमे २, ३ आणि ४ मणी उजवीकडे सरकवावे लागतील (पहा : आकृती). ज्या तारेवर उजवीकडे मणी नाही त्या स्थानी शून्य समजायचे.
गोटीचौकट वापरून बेरीज करण्याची रीत पुढीलप्रमाणे आहे : समजा, ४३२ आणि ४६ यांची बेरीज
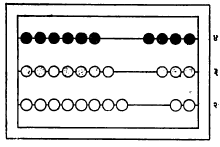
करावयाची आहे. प्रथम वर दिल्याप्रमाणे गोटीचौकटीवर ४३२ घ्या. नंतर एकं-तारेवर आणखी सहा मणी (४६ या दुसऱ्या संख्येतील एकं स्थानातील आकडा) उजवीकडे सरकवा. हे केल्यानंतर एकं-तारेवर आता आठ मणी झाले. तसेच दहं-तारेवर आणखी चार मणी सरकवा. म्हणजे ४३२ + ४६ = ४७८ ही बेरीज मिळेल. या रीतीने मणी सरकवत असता एकं-तारेवर जेव्हा उजवीकडे दहा मणी होतील तेव्हा ते सर्व डावीकडे सरकवून त्याऐवजी दहं-तारेवरील आणखी एक मणी उजवीकडे सरकवायचा. याचप्रमाणे दहं-तारेवरील दहा मण्यांकरिता शतं-तारेवरील एक मणी आणि तसेच इतर स्थानांसाठी करावयाचे. यावरून बेरीज करीत असता हातचा का आणि कसा घ्यायचा याचे तत्त्व समजून येते.
वजाबाकी करताना गोट्या डावीकडे सरकवायच्या (बेरजेच्या उलट) हे उघड आहे. गुणाकार करायचा झाल्यास पुनःपुन्हा बेरीज करावयाची आणि भागाकार म्हणजे पुनःपुन्हा वजाबाकी करावयाची. अर्थात हे काम बरेच जिकीरीचे होते.
पूर्वीच्या काळी साध्या धूळपाटीवरील रेषा आणि दगडांचे वा अन्य वस्तूंचे तुकडे गणितकृत्ये करण्यासाठी वापरीत असत आणि एखाद्या कोष्टकाप्रमाणे त्याचे स्वरूप असे. काही वेळा गोटीचौकटीत तारा उभ्याही वापरल्या जात असत. दशमान पद्धती मूळची हिंदूंची व गोटीचौकट वापरण्याची पद्धती तीवर आधारलेली आहे. भूमध्य समुद्रालगतच्या देशांत तेथे दशमान पद्धती पोहोचण्याच्या बऱ्याच आधीपासून गोटीचौकट वापरात होती. तथापि हिरॉडोटस (ख्रि. पू. ४५०) यांच्या लेखनावरून असे दिसून येते की, ईजिप्तमध्ये व ग्रीसमध्ये अंकस्थाने मोजण्याच्या पद्धती परस्परांच्या विरुद्ध होत्या. जपानमध्ये अद्यापही गोटीचौकट वापरात आहे.
दशमान पद्धतीप्रमाणेच पाच अगर इतर कोणताही मूलांक घेऊन गोटीचौकट तयार करता येईल आणि त्यानुसार अंक दर्शविण्याच्या व त्यांवरील गणितकृत्ये करणाच्या पद्धतीही बसविता येतील.
गुर्जर, ल. वा.
“