चुंबकीय क्षेत्रमापक

चुंबकीय क्षेत्रमापक : एखाद्या ठिकाणची चुंबकीय क्षेत्राची तीव्रता मोजण्याचे साधन. पृथ्वीच्या क्षेत्राची तीव्रता मोजणारे साधन, अशाच अर्थाने बहुधा याचा उपयोग करतात. पृथ्वीच्या चुंबकीय क्षेत्राची दिशा त्याच्या दिक्‌पात (चुंबकीय उत्तर-दक्षिण दिशा व भौगोलिक उत्तर-दक्षिण दिशा यांमधील कोन) व नती (चुंबकीय कोन व त्याचा क्षितिज समांतर घटक यांतील उभ्या प्रतलात मोजलेला कोन) या दोन कोनांनी ठरविली जाते. त्याची तीव्रता क्षेत्रमापकाने मोजतात. पृथ्वीच्या संपूर्ण चुंबकीय क्षेत्राचा (I) क्षैतिज (क्षितिज समांतर) घटक (H) साधारणपणे क्षेत्रमापकाने मोजतात व संपूर्ण क्षेत्राची दिशा जाणून त्यावरून I किती आहे, याचे गणन केले जाते.

चुंबकीय क्षेत्रमापक तीन प्रकारचे आहेत. (१) निरपेक्ष चुंबकीय क्षेत्रमापक : यामध्ये फक्त लांबी, वस्तुमान व काळ या मूलभूत एककांच्या संदर्भाने क्षेत्राचे मूल्य काढतात. (२) सापेक्ष चुंबकीय क्षेत्रमापक : यामध्ये एखाद्या चुंबकीय क्षेत्राशी H ची तुलना केली जाते व त्यावरून त्याचे मूल्य काढतात. (३) चल क्षेत्रमापक : यामध्ये पृथ्वीच्या चुंबकीय क्षेत्रात होणारे स्थल-काल सापेक्ष बदल मोजतात. अशी मापने चंद्र व शुक्र यांच्या पृष्ठभागांजवळही घेण्यात आलेली आहेत. तिन्ही प्रकारचे क्षेत्रमापक उपयोगात असले, तरी दुसऱ्या प्रकारचे क्षेत्रमापक जास्त प्रचारात आहेत. या प्रकारांत एकदिश (एकाच दिशेने वाहणारा) विद्युत् प्रवाह किंवा प्रत्यावर्ती (उलट सुलट दिशेने वाहणारा) विद्युत् प्रवाह यांच्या संदर्भाने क्षेत्राचे मापन केले जाते.

निरपेक्ष चुंबकीय क्षेत्रमापक : पृथ्वीच्या चुंबकीय क्षेत्राचा क्षैतिज घटक (H) निरपेक्ष रीतीने कसा काढावा, हे प्रथम गौस यांनी दाखविले व त्याच पद्धतीने तो अद्यापिही काढतात. या पद्धतीत एक लहान चुंबक सूची एका बारीक बिनपिळाच्या रेशमी धाग्याने टांगती ठेवतात. ही सूची उत्तर-दक्षिण दिशेत स्थिर होते. सूचीपासून काही अंतरावर एखादा कांड चुंबक पूर्व-पश्चिम दिशेने, पण वरील सूचीचा मध्य त्याच्या अक्षावर राहील अशा रीतीने ठेवल्यास त्याच्या क्षेत्रामुळे सूचीचे लहानशा कोनातून विचलन (स्थानबदल) होते. मोजपट्टी, आरसा व दिवा यांच्या साहाय्याने सूचीचा विचलन कोन मोजता येतो. याकरिता रेशमी धाग्याला एक लहानसा आरसा जोडतात व त्यावर दिव्याचा प्रकाश पाडून परावर्तित किरण आरशापासून एक मी. अंतरावर ठेवलेल्या मोजपट्टीवर पडेल अशी मांडणी करतात. सूची विचलित झाली म्हणजे परावर्तित किरण दुप्पट कोनातून फिरतो व त्याचे मोजपट्टीवरील स्थान बदलते. परावर्तित किरणांचे मोजपट्टीवरील मूळ स्थान व बदललेले स्थान यांतील अंतर मोजून सूचीचा विचलन कोन काढता येतो. त्यावरून ^M/_H चे मूल्य काढता येते. येथे M हे कांड चुंबकाचे चुंबकीय परिबल (चुंबकाच्या एका ध्रुवाची तीव्रता व त्याच्या दोन ध्रुवांमधील अंतर यांचा गुणाकार) आहे. चुंबकीय सूची अतिशय बारीक धाग्याने टांगलेली असल्यामुळे तिच्या विचलनाने धाग्याला पीळ बसतो म्हणून मोजलेल्या विचलन कोनात दुरूस्ती करावी लागते. तसेच वरील कांड चुंबक अशाच बारीक धाग्याने टांगून पृथ्वीच्या क्षैतिज चुंबकीय घटकात त्याचे दोलन झाले, तर त्याच्या दोलनाचा आवर्तकाल (एका दोलनास लागणारा काळ) M H वर अवलंबून असतो. आवर्तकाल मोजल्यास M H चे मूल्य काढता येते. याही खेपेस धाग्यात पडणाऱ्या पिळाच्या परिणामासाठी दुरूस्त करावी लागते. ^M/_H व M H या दोन ज्ञात राशींवरून H चे मूल्य काढता येते.

सापेक्ष (तौलनिक) चुंबकीय क्षेत्रमापक : क्वॉर्ट्‌झ क्षैतिज चुंबकीय क्षेत्रमापक (QHM) या नावाने ओळखण्यात येणारा एक प्रकारचा सापेक्ष क्षेत्रमापक पुष्कळ वेळा वापरण्यात येतो. या उपकरणात एक चुंबक अतिशय बारिक पण स्थितिस्थापक (विकृती उत्पन्न करणाऱ्या प्रेरणा काढून घेतल्यावर पुन्हा मूळ स्थितीत येण्याचा गुणधर्म असणाऱ्या) अशा क्वॉर्ट्‌झच्या धाग्याने टांगलेला असतो. त्यावर एक लहानसा आरसा चिकटविलेला असतो. या आरशाला ज्याचा अक्ष लंब आहे असा एक दूरदर्शक बसविलेला असतो. या दूरदर्शकाच्या नेत्रिकेत (डोळ्याशी लावावयाच्या भिंगात) एक पारदर्शक मोजपट्टी बसविलेली असते. (या नेत्रिकेला गौस नेत्रिका म्हणतात). ही मोजपट्टी प्रकाशमान केली असता तिचे वरील आरशातील प्रतिबिंब दूरदर्शकातून दिसू शकते. मोजपट्टीवरील अ या विशिष्ट रेषेचे प्रतिबिंब जेव्हा बरोबर त्याच रेषेवर पडते तेव्हा दूरदर्शकाचा अक्ष आरशाला बरोबर लंब असतो. हे संबंध उपकरण एका उभ्या अक्षाभोवती फिरविता येते व हा फिरविलेला कोन एका वर्तुळाकार कोनमापक पट्टीच्या साहाय्याने अचूक मोजता येतो.

प्रथम उपकरण चुंबकीय दक्षिणोत्तर रेषेला समांतर ठेवून दूरदर्शकाचा अक्ष आरशाला लंब करून घेतात. मग सबंध उपकरण (समजा घड्याळाच्या काट्यांच्या दिशेने) हळूहळू फिरवीत जाऊन शेवटी जेव्हा पुन्हा अ रेषेचे प्रतिबिंब बरोबर त्याच रेषेवर पडते तेव्हा उपकरण (३६०^° + α^° ) इतक्या कोनातून फिरलेले असते. येथून उपकरण परत उलट दिशेने २ (३६०^° + α^° ) या कोनातून फिरवल्यास परत अ चे प्रतिबिंब बरोबर अ वरच पडेल. उपकरणाची पहिली स्थिती व दुसरी स्थिती यांवरून २α हा कोन काढतात. H = ^K/ _{sin α} या सूत्रावरून H चे मूल्य काढतात. येथे k हा स्थिरांक असून त्याचे मूल्य टांगलेल्या चुंबकाच्या चुंबकीय परिबलावर, तसेच धाग्याच्या स्थितीस्थापकतेवर अवलंबून असते.

गॅल्व्हानोमीटर पद्धतीचा क्षेत्रमापक : दुसऱ्या एक तौलनिक क्षेत्रमापकात साइन गॅल्व्हानोमीटराचे तत्त्व उपयोगात आणतात [या गॅल्व्हानोमीटरामध्ये साइन म्हणजे त्रिकोणमितीय ‘ज्या’ गुणोत्तरास उपयोग केलेला असतो, → गॅल्व्हानोमीटर]. दोन हेल्महोल्ट्स वेटोळ्यांमधील (सारखीच त्रिज्या असलेल्या आणि समान अक्षावर समांतर बसविलेल्या वेटोळ्यांमधील) अंतराच्या मध्यभागी एक चुंबकीय सूची बारीक धाग्याने टांगलेली असते. प्रथमतः ही वेटोळी चुंबकीय दक्षिणोत्तर उभी असतात म्हणजे ही सूची त्यांच्या पातळ्यांना समांतर असते ह्या वेटोळ्यातून i एवढा विद्युत् प्रवाह जाऊ दिला, तर प्रवाहाने उत्पन्न झालेल्या चुंबकीय क्षेत्रामुळे सूचीची दिशा बदलते. ही वेटोळी उभ्या अक्षाभोवती योग्य दिशेने फिरविली, तर एके ठिकाणी सूची परत वेटोळ्यांना समांतर राहते. जर यासाठी वेटोळी A या कोनातून फिरवावी लागली, तर H चे मूल्य H = ^Gi/_{sin A} या सूत्रावरून काढता येते. G हा स्थिरांक असून त्याचे मूल्य वेटोळ्याची त्रिज्या व त्यातील तारेचे वेढे यांचे मोजमाप करून काढता येते. i प्रवाहाचे अचूक मूल्य चांदीच्या व्होल्टामीटराच्या (चांदीच्या लवणाच्या विद्रावातून विद्युत् प्रवाह जाऊ देऊन आणि विद्युत् अग्रावर जमा झालेल्या चांदीचे मापन करून विद्युत् प्रवाहाचे अचूक मापन करणाऱ्या उपकरणाच्या साहाय्याने काढता येते.

निराकरण पद्धतीचा क्षेत्रमापक : निराकरणाने H चे मूल्य काढण्यासाठी दुसरी एक पद्धत आहे. यामध्ये एक वेटोळे पूर्व-पश्चिम पातळीत ठेवलेले असते म्हणून त्याचा अक्ष H ला समांतर असतो. या वेटोळ्यातून विद्युत् प्रवाह अशा दिशेने वाहू देतात की, त्याचे चुंबकीय क्षेत्र H ला उलट पण त्याच्याशी सममूल्य यावे, म्हणजे वेटोळ्याच्या मध्यभागी ‘निष्पन्न-क्षेत्र’ शून्य येते. या वेटोळ्याच्या मध्यभागी दुसऱ्या एका लहान वेटोळ्याचा मध्य ठेवून ते उभ्या अक्षाभोवती गरगरा फिरविले, तर त्या जागी निष्पन्न-क्षेत्र असल्यास त्या क्षेत्राच्या तीव्रतेवर अवलंबून असणारा प्रत्यावर्ती प्रवाह त्या लहान वेटोळ्यात निर्माण होईल पण त्या ठिकाणी निष्पन्न-क्षेत्र शून्य असले, तर तसा प्रवाह निर्माण होणार नाही. यावरून मध्यभागी निष्पन्न-क्षेत्र नाही हे निश्चितपणे सांगता येते व म्हणून H = Gi या सूत्राचा उपयोग करून H चे मूल्य काढता येते.

जहाजावरील क्षेत्रमापन : जहाजावर H चे मूल्य काढण्यासाठी खालील पद्धत प्रचारात आहे. एका चुंबकीय सूचीच्या वर काही अंतरावर उभ्या अक्षाभोवती फिरविता येईल असा दुसरा एक आडवा कांड चुंबक ठेवलेला असतो. हा कांड चुंबक असा फिरविण्यात येतो की, त्याचा अक्ष सूचीच्या अक्षाशी बरोबर काटकोन करतो. सूची किती कोनामधून (α) फिरते हे मोजतात आणि त्यावरून H = ^k / _{sin α} या समीकरणाने H चे मूल्य काढतात. समीकरणातील k हा स्थिरांक असून तो वरच्या कांड चुंबकाच्या चुंबकीय परिबलावर अवलंबून असतो. दुसरीही एक पद्धत आहे. तीत एका पेटीमध्ये एकावर एक अशा व एकाच अक्षाभोवती फिरू शकणाऱ्या दोन चुंबकीय सूची ठेवलेल्या असतात. साधारपणे या दोन्ही सूची एकावर एक अशा कधीच स्थिर राहत नाहीत म्हणजे त्यांचे अक्ष एकमेकांशी काही कोन करतात. हा कोन H च्या तीव्रतेवर अवलंबून असतो. क्षेत्राची तीव्रता बदलली म्हणजे हा कोन पण बदलतो. क्षेत्र तीव्रता आणि कोन यांमधील परस्परसंबंध एकदा समजला म्हणजे नंतर केव्हाही H चे मूल्य काढण्यासाठी या उपकरणाचा उपयोग करता येतो.

हॉल परिणाम क्षेत्रमापक : हॉल परिणामाचा (याचे वर्णन खाली दिले आहे) उपयोग करून चुंबकीय क्षेत्राचे मापन करता येते. एखाद्या धातूच्या पातळ आयताकृती पट्टीमधून i हा विद्युत्‌ प्रवाह जाऊ दिला व त्याच्यावरील समोरासमोर असलेले अ आणि आ हे बिंदू एका व्होल्टमापकाला (विद्युत् दाब मोजणाऱ्या

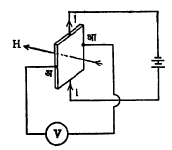
उपकरणाला, V) जोडले, तर आ.१ मध्ये दर्शविलेल्या परिस्थितीत व्होल्टमापकातून विद्युत् प्रवाह जाणार नाही. पण अआ च्या काटकोन दिशेने H हे नवीन चुंबकीय क्षेत्र लावले, तर व्होल्टमापक विद्युत् दाब दाखवील. अशा तऱ्हेने विद्युत् दाब निर्माण होणे या आविष्काराला ‘हॉल परिणाम’ म्हणतात. सर्वच धातूंमध्ये हा परिणाम कमी जास्त प्रमाणात दिसून येत असला, तरी इंडियम अँटिमोनाइड (In Sb) या मिश्रधातूमध्ये तो फारच जोरदार असतो. चुंबकीय क्षेत्र लहान असले, तर निर्माण होणारा विद्युत् दाबही लहान असतो. यासाठी पट्टीभोवती अतिपार्यता असलेले धातूंचे वेष्टन ठेवून तेथील H चे मूल्य अप्रत्यक्षपणे वाढवितात.

प्रोटॉन अनुस्पंदन क्षेत्रमापक : (अनुस्पंदन या संज्ञेच्या स्पष्टीकरणासाठी ‘अनुस्पंदन’ या नोंदीतील ‘अणुकेंद्रीय चुंबकीय अनुस्पंदन’ हा परिच्छेद पहावा). पृथ्वीचे चुंबकीय क्षेत्र अचूक रीतीने मोजण्याची एक नवी पद्धत अलीकडे उपलब्ध झालेली आहे. हीमध्ये प्रोटॉनाच्या चुंबकीय क्षेत्रात होणाऱ्या परांचनाचा (ज्या अक्षाभोवती प्रोटॉन फिरत असतो त्याची दिशा बदलून मूळ दिशेशी व बदल घडवून आणणाऱ्या परिबलाच्या अक्षाशी लंब असणाऱ्या रेषेभोवती तो अक्ष फिरत राहणे या आविष्काराचा) उपयोग केला आहे. यासाठी प्रोटॉनाचे घूर्ण-चुंबकीय गुणोत्तर माहीत असावे लागते (घूर्णचुंबकीय गुणोत्तर म्हणजे कोनीय संवेग व तज्जन्य चुंबकीय परिबल यांचे गुणोत्तर, कोनीय संवेग म्हणजे निरूढी परिबल – कोनीय प्रवेगाला वस्तूने केलेल्या विरोधाचे माप – आणि कोनीय वेग यांचा गुणाकार). या राशीचे मूल्य ऊर्ध्वपातित (वाफ करून मग ती थंड करून मिळविलेल्या) पाण्यातील प्रोटॉनासाठी (२·६७५१३ ± ०.००००२) X १०^४ प्रती सेकंद, प्रती ओर्स्टेड आहे. 

शुद्ध पाणी भरलेले एक भांडे एका परिनलिकाकार (अनेक वेढे असलेल्या दंडगोलाकार) वेटोळ्याच्या मध्यभागी ठेवतात. परिनलिकेचा अक्ष मोजावयाच्या H ला लंब ठेवतात आणि मग वेटोळ्यातून मोठा विद्युत्‌ प्रवाह सोडून त्याच्या आतील भागात सु. १,००० ओर्स्टेड तीव्रतेचे क्षेत्र H_P निर्माण करतात. यामुळे पाण्यातील सर्व प्रोटॉन या क्षेत्राच्या दिशेला समांतर स्थितीत येतात. मग हा विद्युत्‌ प्रवाह एकदम बंद करून H_P शून्य केल्यास प्रोटॉन परांचन करीत H ला समांतर होऊ लागतात. ही क्रिया २-३ सेकंदच टिकते आणि ती चालू असताना त्या वेटोळ्यात काही दशलक्षांश व्होल्ट प्रत्यावर्ती विद्युत्‌ प्रवाह प्रवर्तित होतो. या विद्युत्‌ प्रवाहाची कंप्रता (ही प्रोटॉनाच्या परांचन कंप्रतेइतकीच असते) H च्या सम प्रमाणात असते (कंप्रत म्हणजे दर सेकंदास होणाऱ्या आवर्तनांची संख्या). म्हणून विद्युत्‌ प्रवाहाची कंप्रता इलेक्ट्रॉनीय उपकरणाने मोजून त्यावरून H चे मूल्य काढता येते. या मापनाची अचूकता ± १ γ ( γ  = १०^-५ ओर्स्टेड) इतकी असून मापनाला फारच थोडा वेळ म्हणजे सु. १० सेकंद लागतो. त्यामुळे हल्ली या पद्धतीचा वापर मोठ्या प्रमाणावर करतात. 

स्रोतद्वार पद्धतीचा क्षेत्रमापक : दुसऱ्या महायुद्धात विमानातून पाणबुड्यांचा शोध घेण्यासाठी एक खास क्षेत्रमापक तयार करण्यात आला होता. त्याच्यात आणखी सुधारणा करून तो आता अनेक ठिकाणी वापरला जातो. कारण त्याची अचूकता ०·०१ γ पर्यंत वाढविता येते. जलद जाणाऱ्या वाहनातून मोठ्या प्रदेशाचे चुंबकीय सर्वेक्षण त्याच्या साहाय्याने अगदी थोड्या वेळात करता येते. आंतरराष्ट्रीय भूभौतिक वर्षाच्या संदर्भात पृथ्वीच्या चुंबकीय सर्वेक्षणासाठी त्याचा उपयोग करण्यात आला. भूगर्भातील खनिज साठ्यांचा शोध घेण्यासाठीही या क्षेत्रमापकाचा उपयोग करतात. चंद्रावरील चुंबकीय क्षेत्राच्या मापनासाठीही याचाच उपयोग केला होता. 

या क्षेत्रमापकातील मुख्य घटक म्हणजे म्यू-मेटल (मुंट्झ धातू) किंवा पर्म-ॲलॉय (लोह-निकेल यांपासून बनविलेल्या) यासारख्या मिश्रधातूंची सळई होय. या मिश्रधातूचा मुख्य गुण हा की, अगदी अल्प मूल्याच्या चुंबकीय क्षेत्रात ठेवूनही त्यांना चुंबकीय संपृक्तता प्राप्त होते. एकदा ही संपृक्तता आली की, मग भोवतालचे क्षेत्र कितीही वाढविले, तरी या सळईतून जाणाऱ्या चुंबकीय क्षेत्र रेषांची संख्या वाढू शकत नाही म्हणजेच तिच्यातील चुंबकीय स्रोत वाढत नाही. या तत्त्वावर आधारलेल्या क्षेत्रमापकास स्रोतद्वार क्षेत्रमापक असे म्हणतात. याचे वेगवेगळे प्रकार प्रचारात आहेत. त्यांपैकी अगदी साध्या प्रकारच्या क्षेत्रमापकाची कार्यपद्धती स्थूलमानाने पुढे दिली आहे. 

म्यू-मेटलची एक सळई स घेऊन तिच्यावर अ आणि आ ही दोन अगदी एकसारखी तारेची वेटोळी परस्परांना विरुद्ध दिशेने गुंडाळतात. या दोहोंच्याही वरून प हे प्रवर्तक वेटोळे गुंडाळलेले असते.

अ आणि आ या वेटोळ्यांमधून एकच प्रत्यावर्ती विद्युत्‌ प्रवाह सोडतात. स भोवती बाह्य चुंबकीय क्षेत्र नाही

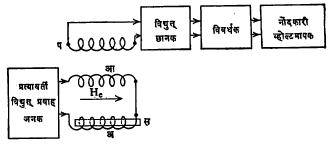
असे मानल्यास अ आणिआ मधील विद्युत्‌ प्रवाहामुळे स मध्ये निर्माण होणारी चुंबकीय क्षेत्रे नेहमी सममूल्य पण परस्परांना विरूद्ध दिशेने असल्याने परस्परांचे पूर्णपणे निराकरण करतात. त्यामुळे स मधील चुंबकीय स्रोत नेहमी शून्य राहून प मध्ये (प्रवर्तनामुळे) काहीही विद्युत्‌ प्रवाह उत्पन्न होत नाही. परंतु स भोवती त्याला समांतर असे H_e हे चुंबकीय क्षेत्र असल्यास ते अत्यंत दुर्बल असले, तरीही स मध्ये जवळजवळ संपृक्तता निर्माण करू शकते. त्यामुळे अ व आ या प्रत्येक वेटोळ्यातील विद्युत्‌ प्रवाहामुळे निर्माण होणारी जादा चुंबकीय क्षेत्रे आपल्या प्रत्येक आवर्तनात अंशतः संपृक्ततेच्या मर्यादेच्या पलीकडे जातात आणि त्यामुळे ती परस्परांचे पूर्ण निराकरण करू शकत नाहीत. यामुळे कालानुसार बदलणारा चुंबकीय स्रोत स मध्ये निष्पन्न होतो. त्यामुळे प मध्ये प्रत्यावर्ती विद्युत्‌ दाब निर्माण होतो. हा दाब H_e च्या सम प्रमाणात असल्याने तो मोजून त्यावरून H_e चे मूल्य काढता येते.

प्रत्यक्ष उपकरणात विद्युत्‌ छानक (निरनिराळ्या कंप्रतांचे विद्युत्‌ तरंग अलग करणारे साधन), विवर्धक (विद्युत्‌ प्रवाहाची शक्ती वाढविणारे साधन) वगैरेंचा अंतर्भाव करून ते अधिक कार्यक्षम व संवेदनशील केले जाते. त्याचप्रमाणे स्वयंचलित नोंद लेखकाची जोड देऊन He च्या मूल्यांची आपोआप नोंद करता येते किंवा जरूर तर ही मूल्ये सांकेतिक संदेशाच्या रूपाने रेडियो तरंगाच्या द्वारा प्रक्षेपितही करता येतात.

संदर्भ : 1. Bleil, D. F. Natural Electromagnetic Phenomena (Proceedings of NATO Advanced Study Institute), New York, 1964.

  2. Chikazumi, S. Physics of Magnetism, New York, 1964.

  3. Hine, A. Magnetic Compasses and Magnetometers, London, 1968.

पाटणकर, भा. वि.

“