गणितीय प्रतिरूपे : कोणत्याही शास्त्रातील पायाभूत कल्पना अर्मूत स्वरूपात मांडल्या, तर त्या सर्वांना सहजगत्या समजतातच असे नाही. पण त्या मूर्तरूपाने पुढे ठेवल्यास त्यांतील तत्व समजण्यास सोपे होते. गणितशास्त्रही या नियमास अपवाद नाही. गणिताच्या कोणत्याही विभागाच्या स्पष्टीकरणार्थ (विशेषत: घन भूमिती, यामिकी म्हणजे प्रेरणांची वस्तूंवर होणारी क्रिया व त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणारे शास्त्र इ.) वर्ण्य वस्तूंची प्रतिरूपे (चित्रे, नमुने वा आकृत्या) समोर असल्यास विषयाचे विवेचन लवकर आणि सुलभतेने समजते.
यासाठी लागणारी चित्रे, फळ्यांवरील आकृती, वस्तूंचे नमुने, छायाचित्रे इ. अनेक प्रकारच्या प्रतीकांना ‘प्रतिरूपे’(मॉडेल्स) असे म्हणतात. वस्तुत: प्राथमिक शिक्षणापासूनच प्रत्यक्ष वस्तूंची प्रतिरूपे वापरावयास सुरुवात होते. गणितीय प्रतिरूप म्हणजे त्या प्रत्यक्ष वस्तूची हुबेहूब प्रतिकृती (लहान प्रमाणात) असेलच असे नाही उदा., एखाद्या सरळ रस्त्यावरून धावणाऱ्या मोटारीचे, एक सरळ रेषा व त्यावरील एक चल (हलणारा) बिंदू हे गणितीय प्रतिरूप होय. तसेच एखादा संच दाखविण्याकरिता एखाद्या बंद वक्रातील भाग (व्हेन आकृती, जॉन व्हेन या तर्कशास्त्रज्ञांच्या नावावरून) हा त्या संचाचे गणितीय प्रतिरूप म्हणून वापरतात.
गणितीय प्रतिरूपांचा मुख्य उद्देश सिद्धांत प्रस्थापित करणे हा नसून त्या सिद्धांताचे निर्देशन करणे हा होय. प्रमेयाची सत्यता प्रतिरूपावरून लगेच पटते व प्रमेय चांगले समजून उत्तम मर्मग्रहण होते. कित्येकदा त्यावरून आणखी काही नवीन कल्पना सुचतात.
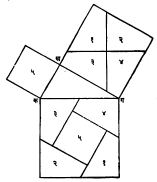
भूमितीय प्रतिरूपे : एकप्रतली (एकाच पातळीतील) किंवा घन भूमितीतील सिद्धांत वा सूत्रे स्पष्ट करण्यासाठी प्रारूपांचा फार उपयोग होतो. खाली दिलेल्या उदाहरणावरून हे अधिक स्पष्ट होईल.
पायथॅगोरस यांच्या, काटकोन त्रिकोणासंबंधीच्या सुपरिचित सिद्धांताची सत्यता खाली दिलेल्या पद्धतीने लगेच पटते. कखग हा काटकोन त्रिकोण आहे (∠ ख= ९००). याच्या कख, खग आणि गक बाजूंवर चौरस काढले. खग वरील चौरसाचे त्याच्या कर्णसंपाती मध्यबिंदूतून कग ला समांतर व लंब अशा रेषा काढून चार भाग पाडले. आता समजा, ही आकृती पुठ्ठ्याची असून, हे भाग कापून आकृतीत दाखविल्याप्रमाणे, कगवरील चौरसात बसवले तर मध्ये उरलेल्या मोकळ्या जागेत कखवरील चौरस बरोबर बसेल आणि पायथॅगोरस सिद्धांताची सत्यता पटेल. समजा, आपल्याला चतु:पृष्ठकाचे प्रतिरूप बनवावयाचे आहे. एका जाड कागदावर क ख ग त्रिकोण काढा. Δ क प ग, Δ ख म ग, Δ क फ ग असे काढा की गप = गम, कप = कफ आणि खफ = खम असेल (आ. २).मात्र ∠ पकग व ∠ फकख यांची बेरीज ∠ गकख पेक्षा कमी असता कामा नये. याचप्रमाणे ग व ख या बिंदूपाशील कोनांबाबत खबरदारी घ्यावी. तयार झालेली आकृती कापून खक, खग, गक पाशी असे दुमडा की गप, गम, खफ, खम, कप, कफ एकमेकांशी जुळतील आणि प, फ, म एकाच ब या शिरोबिंदूत मिळतील. अशा तऱ्हेने चतु:पृष्ठक मिळेल. अशा प्रतिरूपाच्या साहाय्याने घन भूमितीतील चतु:पृष्ठकासंबंधीची प्रमेये व सूत्रे सहजपणे पडताळून पाहता येतात. घडी घालण्यापूर्वीची एकप्रतली आकृती म्हणजे चतु:पृष्ठकाचा एकतल विकास होय.
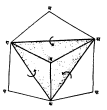
याचप्रकारे इतर बहुपृष्ठकांचीही प्रतिरूपे तयार करतात. त्यावरून तत्संबंधीची प्रमेये, सूत्रे व सिद्धांत पडताळून पाहता येतात. उदा., बहुपृष्ठकाविषयीचा ऑयलर यांचा सिद्धांत श + पृ = क + २ (श-शिरोबिंदूंची संख्या, पृ –पृष्ठांची संख्या, क-कडांची संख्या) याची सत्यता तपासून पाहता येते.
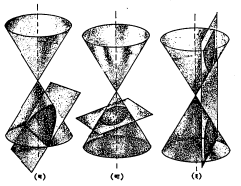
शंकुच्छेद : कोणत्याही जात्यवृत्त (ज्याचा पाया वर्तुळाकृती असून अक्षाला पाया लंब आहे अशा) शंकूचा एखाद्या प्रतलाने छेद घेतला तर तो वर्तुळ, अन्वस्त (पॅराबोला), विवृत्त (लंबवर्तुळ), अपास्त (हायपरबोला) वा दोन परस्परछेदक रेषा यांपैकी कोणतातरी एक वक्र मिळतो. आकृतीमध्ये दाखविल्याप्रमाणे लाकडाच्या (वा अन्य पदार्थाच्या) प्रतिरूपाच्या साहाय्याने हे स्पष्टपणे दाखविता येते [→ शंकुच्छेद].
एकपृष्ठी अपास्तज : ही एक डमरूसारखी दिसणारी घनाकृती आहे. त्याचे प्रतिरूप पुढे दिल्याप्रमाणे करता येते. एक वर्तुळाकार कडे घ्या. त्यावर क, ख, ग … हे बिंदू समान अंतरावर स्थापा. तसेच दुसरे हुबेहूब तसेच वर्तुळाकार कडे पहिल्याच्या बरोबर खाली समांतर असे घेऊन त्यावर क‘, ख‘, ग‘ … असे समान (वरील इतक्याच) अंतरावर बिंदू घ्या. आता कक‘, खख‘, गग‘, … अशा बिंदूंच्या जोड्या सरळ तारांच्या साहाय्याने सांधा.
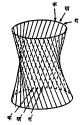
खालचे कडे त्याच्याच पातळीत थोडेसे फिरविले म्हणजे आ. ४ मध्ये दाखविल्याप्रमाणे आपल्याला एकपृष्ठी वृत्तीय अपास्तज मिळेल (कक‘, खख‘ इ. तारा कड्याच्या पृष्ठास लंब असणार नाहीत). या बिंदूंची संख्या जितकी जास्त तितके चांगले प्रतिरूप मिळेल. जर वर वापरलेली दोन कडी विवृत्ताकार असतील तर विवृत्ती अपास्तज मिळेल आणि अन्वस्ताकार असतील तर अन्वस्ती अपास्तज मिळेल. अशा तऱ्हेने तयार केलेल्या प्रतिरूपावरून अपास्तज हे रेखांकित पृष्ठ (एक सरळ रेषा फिरविण्याने तयार होणारे पृष्ठ) कसे उत्तम रीतीने समजते.तसेच त्यासंबंधी इतर अभ्यासही सुलभ होतो.
अशी इतर त्रिमिती पृष्ठांची प्रतिरूपे निरनिराळ्या सोयीस्कर कृती व माध्यमे वापरून तयार करता येतात.
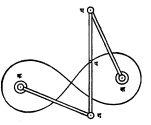
एकप्रतली वक्र : समजा, दोनपट्ट्यांची टोके अशा तऱ्हेने जोडली की, त्यांच्या प्रतलात फिरताना सांध्यापाशी काहीही अटकाव होत नाही. निरनिराळ्या पट्ट्या अशा रीतीने जोडून त्यांच्या गतीपासून यांत्रिक पद्धतीने कोणत्याही बैजिक समीकरणाचा प्रातिनिधिक वक्र काढता येतो असे केंप यांनी १८७५ साली सिद्ध केले. अर्थात किती कशा पट्ट्या वापरावयाच्या हे त्या समीकरणावर अवलंबून राहील. उदा., कग, गघ आणि घख या तीन पट्ट्या ग आणि घ येथे वर दिल्याप्रमाणे सांधल्या (आ. ५). आता एका कागदावर क आणि ख हे स्थिर ठेवून, या पट्ट्या शक्य त्या सर्व प्रकारे फिरविल्या. गघ वरील प या जागी जर एक छिद्र ठेऊन त्यातून एक पेन्सिल घातली, तर त्यायोगे कागदावर बेर्नुली यांचा द्विपर्ण वक्र मिळतो.
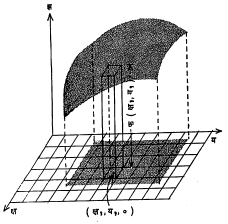
वस्तुत: क्ष य मधील बैजिक समीकरण म्हणजे त्या चलांमधील फलनसंबंध आणि त्याचा वक्र म्हणजे त्या फलनाचे भूमितीय प्रतिरूप होय. तसेच तीन चलांमधील फलनाचेही भूमितीय प्रतिरूप (पृष्ठ) तयार करता येते. उदा., झ = फ (क्ष, य) हे फलन घेऊ. क्ष, य, झ हे परस्पर लंब असे अक्ष घ्या (क्ष य प्रतल क्षितिज समांतर). क्षय प्रतलाच्या क्ष अक्षास आणि य अक्षास समांतर अशा रेषांनी शक्य तितके लहान असे चौरस भाग पाडा. त्यातील एका चौरसाचा मध्यबिंदू समजा (क्ष१ य१, ०) आहे तर तो चौरस पाया घेऊन त्यावर फ (क्ष१, य१) इतक्या उंचीची यष्टी उभी करा. याचप्रकारे सर्व चौरसांवर यष्टी उभ्या असताना, त्या यष्टींच्या दुसऱ्या टोकांमुळे तयार झालेले जे पृष्ठ मिळेल ते गुळगुळीत केले असता झ = फ ( क्ष, य) या फलनाचे प्रतिरूप मिळेल. यामध्ये चौरस जितके लहान तितके पृष्ठ चांगले मिळेल हे उघड आहे (आ. ६).
यंत्र निदर्शक प्रतिरूपे : लहानमोठी अशी अनेक यांत्रिक वा विद्युत् उपकरणे आपल्या नित्य व्यवहारात वापरात असतात. यात सामान्यपणे एका प्रकारच्या शक्तीने दुसऱ्या प्रकारच्या शक्तीत रूपांतर करणे, गती कमीजास्त करणे इ. मूलभूत तत्त्वे असतात. अशा उपकरणांची प्रतिरूपे दोन प्रकारची असू शकतात. त्या उपकरणाची लहान प्रमाणात हुबेहूब प्रतिकृती अथवा ते उपकरण ज्या तत्त्वावर चालते ते तत्त्व मुख्यत: विशद करणारी आकृती. यातील दुसरा प्रकार म्हणजे त्या उपकरणाची गणितीय प्रतिकृती होय. स्थापत्यातील नकाशे, अभियांत्रिकीतील आकृत्या इ. याच प्रकारात मोडतात.
संस्थितिविज्ञानातील प्रतिरूपे : जर एखादा वक्र कोठेही न तोडता दुसऱ्या वक्राशी एकरूप करता येत असेल, तर ते दोन्ही वक्र ⇨संस्थितिविज्ञानात समान मानले जातात. हे एखाद्या लवचिक तारेच्या साहाय्याने उत्तम रातीने दाखविता येते. तसेच जर एखादे पृष्ठ सतत बदलाने कोठेही न तोडता दुसऱ्या पृष्ठात परिणित होऊ शकत असेल, तर ती पृष्ठे संस्थिती दृष्ट्या समान मानतात. एखाद्या लवचिक पदार्थाचे पृष्ठ तयार करून त्यात बदल करून हे दाखविता येईल. तसेच घनाकृती किंवा प्रस्थासंबंधी म्हणता येईल. या संकल्पना प्रतिरूपांच्या साहाय्याने सुलभ रीतीने स्पष्ट करता येतात. उदा., वर्तुळ आणि चौकोन हे समान वक्र आहेत, गोलाचा आणि अंड्याचा पृष्ठभाग ही समान पृष्ठे आहेत तसेच घन-गोल आणि घन ही समान प्रस्थे आहेत.
याप्रमाणेच एक संबद्ध, द्विसंबद्ध पृष्ठभाग इ. संकल्पना प्रतिरूपांच्या साहाय्याने स्पष्ट करता येतात. एखाद्या रबराच्या पृष्ठावर वक्र काढला आणि त्या पृष्ठाच्या आकुंचनाने किंवा ताणण्याने जे अनेक वक्र मिळतात ते मूळ वक्राला समान असतीलच. अशांच्या गुणधर्मांचा अभ्यास संस्थिती विश्लेषणात होतो. त्यामुळेच गमतीने त्या शास्त्रास रबर-पृष्ठाची भूमिती असे म्हटले जात असे.
त्रिमितिदर्शक व प्रकाशीय प्रतिरूपे :सपाट पृष्ठावर काढलेला फोटो किंवा चित्र दिलेल्या वस्तुविषयाची त्रिमितिदर्शक प्रतिमा डोळ्यांसमोर हुबेहुब उभी करू शकत नाही. त्यामुळे घन भूमिती समजण्यास अडचणी येतात. त्या नाहीशा करण्यासाठी ज्या क्लृप्त्या योजतात त्यांचे सामान्यत: खालील तीन प्रकार होतात.
(१) त्रिमितिदर्शक यंत्र :यात निरिक्षकाच्या डोळ्यास लावण्यास दिलेला एक चष्मा असतो. त्याच्या काचा बहिर्वक्र किंवा अर्धबहिर्वक्र असतात. जो देखावा पहावयाचा त्याची दोन चित्रे किंवा छायाचित्रे दोन जवळच्या स्थानावरून काढतात. नंतर तयार झालेले जोड छायाचित्र अथवा जोडचित्र चष्म्यापुढे काही अंतरावर तारपट्टीत ठेवतात. चष्म्याची भिंगे व चित्र यांतील अंतर कमीजास्त करण्याची व्यवस्था असते. निरिक्षक प्रथम बघतो त्यावेळी वस्तुविषय त्रिमितिरूपात एकदम दिसत नाही. पण दोन्ही डोळ्यांच्या प्रतिमा एकरूप होताच चित्रास खोली किंवा उठाव दिसू लागतो [→ त्रिमितिदर्शक].
(२) त्रिमितिदर्शक वर्णयंत्र : यात वस्तुविषयाची लाल व निळ्या रंगात काढलेली चित्रे मधे एक अवशोषक पडदा घालून प्रेक्षकाच्या डोळ्यांपुढे धरतात. दोन्ही डोळ्यांच्या प्रतिमा एकरूप होताच चित्राला घनता प्राप्त होते. लुई ड्युको द हारून यांनी हे यंत्र शोधून काढले.
ॲर्नोल्ड एंच यांनी चित्रदीपाच्या (मॅजिक लँटर्नच्या) काचा विशिष्ट तऱ्हेने रंगवून पुष्कळ बैजिक वक्रांची त्रिमिती रूपे सुस्पष्ट केली. तसेच पाँस्ले बहुकोनाकृती चित्रपटाच्या द्वारे समजावून दिली.
(३) चलत्-आवरणिक प्रक्षेपण यंत्र : चित्रदीपाच्या ज्योतीपुढे एका पेटीत एक फिरते चाक ठेवतात. त्याच्या वरच्या बाजूस एक पातळ पारदर्शक पडदा फिरता ठेवतात. केंद्रकारकाला (प्रकाश किरणांचे केंद्रीकरण करणाऱ्या भिंगाला) समांतर अशा उभ्या पातळीत हा पडदा फिरतो व त्यावर तारांचे तुकडे चिकटविता येतात. या तारांच्या छाया चित्रदीपाच्या भिंगातून पुढे जाऊन पडद्यावर पडतात. भिंगाच्या पुढे गोल, शंकू, वृत्तचिती किंवा कोठलेही तारांचे बनलेले प्रतिरूप ठेवता येते. प्रतिरूपाच्या छायाचित्रात या फिरत्या रेषांनी कर्ण, मध्यगा इ. रेषांची समज चांगल्या तऱ्हेने देता येते. हे यंत्र फ्रीबर्ग येथील पॅपेरिट्झ यांनी बनविले होते.
संदर्भ : Cundy, C. H. Rollet, A. P. Mathematical Models, Oxford, 1961.
फडके, ना. ह. आगाशे, क. म.
“