गणकपट्टी: (स्लाइड रूल). गणितकृत्ये जलद रीतीने करण्यास मदत करणारे एक उपकरण. गणकपट्टीच्या साहाय्याने मुख्यतः गुणाकार, भागाकार, घात व घातमुळे काढता येतात. काही गणकपट्ट्यांवर त्रिकोणमितीय गुणोत्तरेही दिलेली असतात. सर्वसाधारण वापरण्यात येणाऱ्या गणकपट्ट्या सरळ आकाराच्या असतात, पण काही वर्तुळाकारही असतात. वर्तुळाच्या परिघाची लांबी व्यासाच्या तिपटीपेक्षा अधिक असल्यामुळे वर्तुळाकार गणकपट्टीत परिघावर अधिक मापनबिंदू मावू शकतात. गणकपट्टीच्या साहाय्याने सामान्यतः दोन दशांश स्थळांपर्यंत अचूक गणितकृत्ये करता येतात. सुरूवातीस गणकपट्ट्या धातूच्या बनविण्यात येत, परंतु त्यांच्यावर हवेतील आर्द्रतेचा परिणाम होत असल्याने आता त्या बनविण्यासाठी हस्तिदंत, सेल्युलॉइड किंवा प्लॅस्टिक वापरतात.

गणकपट्टीचे सांगाडा, सरकपट्टी व केशरेषाधारक असे तीन भाग असतात. सांगाड्यात वर व खाली सारख्या लांबीच्या दोन समांतर पट्ट्या असून त्या दोहोंमध्ये खोबणीत सहज रीतीने मागेपुढे सरकविता येणारी सरकपट्टी असते. केशरेषाधारक म्हणजे एक लहानसा पारदर्शक चौकोनी तुकडा असून त्यावर मधोमध सांगाड्यातील पट्ट्या आणि सरकपट्टी यांना लंब असलेली केसासारखी एक सूक्ष्म रेषा (केशरेषा) असते. हा केशरेषाधारक सर्व पट्ट्यांवरून सहजपणे सरकविता येतो व केशरेषा इच्छित जागी आणता येते. आ.१ मध्ये गणकपट्टीचे सर्व भाग दाखविले आहेत.


सरकपट्टीच्या दोन्ही कडांवर तसेच सांगाड्यातील पट्ट्यांवर (वरच्या पट्टीच्या खालच्या कडेवर व खालच्या पट्टीच्या वरच्या कडेवर) मापनबिंदू स्थापिलेले असतात. सरकपट्टीवरील मापनबिंदू सांगाड्याच्या स्थिर पट्ट्यांवरील मापनबिंदूंशी तंतोतंत जुळतात. हे मापनबिंदू १, २, ३,….. इत्यादींनी दर्शविलेले असतात. त्यांना निर्देशांक म्हणतात. या निर्देशांकांचे मापन लॉगरिथमधील असल्यामुळे १ व २ मधील अंतर, २ व ३ मधील अंतर इ. सारखी नसतात. उदा., लॉग २ दर्शविणारी लांबी ०·३०१ आहे पण त्यावरील निर्देशांक २ असतो. लॉग ३ दर्शविणारी लांबी ०·४७७ आहे पण त्यावरील निर्देशांक ३ असतो. याप्रमाणे १ पासून १० पर्यंतचे निर्देशांक स्थापन केलेले असतात. या लांब्या प्रमाणित करण्यासाठी क्ष = लॉग१० य याआलेखाचा उपयोग करतात.
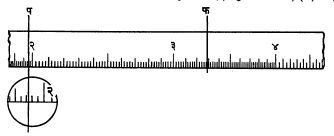
आ. २ मध्ये सरकपट्टी व सांगाड्यातील खालची पट्टी दाखविलेली असून त्यावरील मापक्रमांचे मुख्य भाग दाखविलेले आहेत. सरकपट्टीवरील मापक्रमास क मापक्रम आणि सांगाड्यातील मापक्रमास ड मापक्रम असे म्हणू. या मापक्रमांचे मुख्य भाग आ. २ मध्ये दिलेले आहेत व आ. ३ मध्ये ड मापक्रम मोठा करून दाखविला आहे.
आ. ३ मध्ये १ आणि २ यांतील अंतर इतर निर्देशांकांमधील अंतरांच्या मानाने मोठे आहे. त्यात दहा विभाग असून प्रत्येक विभाग आणखी दहा पोटविभागांत विभागला आहे आणि प्रत्येक विभागावर अंकावली लिहिली आहे. २ आणि ४ मधील प्रत्येक विभाग पाच पोटविभागांत ४ ते १० मधील प्रत्येक विभाग दोन पोटविभागांत विभागला आहे. १ आणि २ मधील प्रत्येक पोटविभागाचे मूल्य ०·०१ २ व ४ मधील प्रत्येकाचे मूल्य ०·०२ आणि ४ व १० मधील प्रत्येकाचे मूल्य ०·०५ आहे. आ. ३ मध्ये हे सर्व विभाग व पोटविभाग दाखविले आहेत.अशा रीताने ड मापक्रमावरील मापनबिंदूंचे प्रमाणीकरण करण्यात येते.
केशरेषा निरनिराळ्या ठिकाणी असताना क मापक्रम कसा वाचावा हे आ. ४ मध्ये, हा मापक्रम मोठा करून, दर्शविले आहे. या आकृतीत प आणि फ रेषांनी या केशरेषेच्या दोन जागा दर्शविल्या आहेत. त्या पुढीलप्रमाणे वाचतात : (१) केशरेषेची प ही जागा १ आणि २ या भागांमध्ये पडते म्हणून पहिला आकडा १ (२) केशरेषा पूर्ण ९ विभागाच्या पुढे आहे म्हणून दुसरा आकडा ९ (३) ती पूर्ण ७ पोटविभागापुढे आहे म्हणून तिसरा आकडा ७ (४) ती ७ व ८ या पोटविभागाच्या साधारपणे तिसऱ्या हिश्यावर पडते (खाली वर्तुळात मापक्रम आणखी मोठा करून दाखविला आहे) म्हणून चौथा आकडा ३ (कारण १/३ = ०·३). हे सर्व आकडे मिळून प स्थानीच्या केशरेषेचे वाचन १·९७३ असे आहे. याचप्रमाणे फ स्थानीच्या केशरेषेचे वाचन करता येईल.
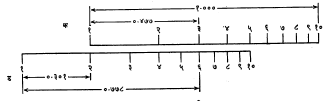
गणितकृत्ये करण्याची पद्धती: गुणाकार करताना ज्या आकड्याला गुणावयाचे असेल त्या ड मापक्रमावरील आकड्यावर सरकपट्टीवरील १ हा निर्देशांक ठेवून ज्याने गुणावयाचे असेल त्या सरकपट्टीवरील क मापक्रमावरील आकड्यावर केशरेषा जुळेल इतका केशरेषाधारक सरकवितात. केशरेषाखालील ड मापक्रमावर दिसणारी संख्या गुणाकार दर्शविते. यात लॉग (प फ)= लॉग(प)+लॉग(फ) हे गणितीय समीकरण वापरले आहे. आ. ५ मध्ये लॉग ६ = लॉग २+लॉग ३ हे दर्शविले आहे.
भागाकारात लॉग (प/फ) = लॉग प–लॉग फ हे समीकरण उपयोगात आणले जात असल्याकारणाने ज्याला भागावयाचे त्या ड मापक्रमावरील आकड्याशी, ज्या आकड्याने भागावयाचे तो सरकपट्टीवरील क मापक्रमावरील आकडा जुळेल इतकी सरकपट्टी सरकवितात व केशरेषाधारक सरकपट्टीवरील १ या निर्देशांकावर आणतात. केशरेषाखालील ड मापक्रमावरील संख्या भागाकार दर्शविते. मात्र गुणाकारात सरकपट्टी उजव्या बाजूस सरकवावी लागली, तर भागाकारात ती डाव्या बाजूस सरकावावी लागेल हे उघड आहे.
गणितकृत्यात मोठमोठ्या संख्या आल्यास त्यांच्या बाबतीत दशांश चिन्हाचा उपयोग करता येतो. उदा., २९५ × १३४ हा गुणाकार करण्यासाठी २९५ = २·९५ × १०२ आणि १३४ = १·३४ × १०२ असे लिहून २·९५ × १·३४ यांचा गणकपट्टीने गुणाकार करता येतो व योग्य ठिकाणी दशांश चिन्ह देऊन अंतिम गुणाकार लिहिता येतो.
सांगाड्याच्या वरच्या पट्टीवरील मापक्रमास अ मापक्रम म्हणतात. केशरेषा कोठेही ठेवल्यास केशरेषेखालील अ मापक्रमावरील आकड्याचे वर्गमूळ ड मापक्रमावर मिळते.
गणकपट्टीची उपयुक्तता वाढविण्यासाठी सांगाड्यातील वरच्या पट्टीवर त्रिकोणमितीय स्पर्शक व कोस्पर्शक गुणोत्तरांचे मापनबिंदू ०० ते ४५० पर्यंत आणि उलट दिशेने ४५० ते ८९·४५० दिलेले असतात. सांगाड्यातील खालच्या पट्टीवर ड मापक्रम देणारे मापबिंदू आणि ज्या व कोज्या ही त्रिकोणमितीय गुणोत्तरे ५·५० ते ९०० पर्यंत आणि उलट दिशेने ०० पासून ८४·५० पर्यंत दिलेली असतात. याशिवाय सरकपट्टीच्या मागील बाजूस आणि सांगाड्याच्या वरच्या व खालच्या कडांवर काही विशेष प्रकारचे मापक्रमही अंतर्भूत करण्यात येतात.
या सर्व सोयींमुळे जलद गणितकृत्ये करण्यासाठी शास्त्रज्ञांना आणि विशेषतः अभियंत्यांना गणकपट्टी अतिशय उपयुक्त ठरली आहे.
संदर्भ : 1. Arnold, J. N. Slide Rule : Principles and Applications, Englewood Cliffs, N.J., 1954.
2. Bishop, C. C. Slide Rule : How to Use It, New York, 1955.
3. Perrine, J. O. The Slide Rule Handbook, New York, 1964.
गुर्जर, ल. वा.
“