पुंज क्षेत्र सिद्धांत : मूलकणांमधील [→ मूूलकण] परस्पर क्रियेचे विशदीकरण करण्याकरिता पुंज क्षेत्र सिद्धांताचा उपयोग केला जातो. या सिद्धांतामध्ये ⇨ पुंजयामिकी व सर्वसाधारणपणे मर्यादित सापेक्षता सिद्धांत [→ सापेक्षता सिद्धांत] यांमधील तत्त्वे वापरली जातात. ज्यामधील परस्परक्रियेचे वर्णन करावयाचे ते मूलकण विद्युत् भारित असले पाहिजेतच असे नाही, कारण विद्युत् चुंबकीय क्षेत्रामध्येच नव्हे, तर गुरुत्वीय व अणुकेंद्रीय क्षेत्रामध्ये सुद्धा कणाच्या होणाऱ्या वर्तणुकीचे विश्लेषण करण्याकरिता हाच सिद्धांत उपयुक्त ठरतो. मूलकणांचे गुणधर्म, त्यांच्या निर्मिती व विनाश विक्रिया इ.गोष्टींचे विवरण या सिद्धांताच्या साहाय्याने करता येते. अणुकेद्रांत प्रोटाॅन आणि न्युट्रॉन हे मूलकण बंधित स्वरूपात का असतात याचाही खुलासा या सिद्धांतावरून मिळतो.
क्षेत्र व त्याचे पुंजीकरण : रुढ भौतिकीत क्षेत्र या कल्पनेचा वापर पूर्वीपासूनच केला जात होता. न्यूटन(१६४२–१७२७) यांनी उपयोगात आणलेले गुरुत्वीय क्षेत्र किंवा मायकेल फॅराडे (१७९१–१८६७) व जे. सी. मॅक्सवेल (१९३१–७९) यांना अभिप्रेत असलेले विद्युत् चुंबकीय क्षेत्र, ही रूढ क्षेत्राची उदाहरणे म्हणुन देता येतात. याउलट अणूकेंद्रांत असणारे अणूकेंद्रीय क्षेत्र अथवा अणूच्या अंतर्गत असणारे अणूकेद्र व इलेक्ट्रॉन यांमधील विद्युत् चुंबकिय क्षेत्र ही पुंज क्षेत्रे आहेत असे म्हणतात. भौतिकामध्ये रूढ व पुंज अशा दोन क्षेत्रांचा उल्लेख होत असला, तरी खरे पाहिले असता रूढ क्षेत्र हे पुंज क्षेत्राचे स्थूल स्तराकरिता फक्त यथार्थ ठरणारे असे आसन्न समीप वा बहुतांशी स्वरूप आहे असे म्हणता येईल की, ज्ञात असलेली क्षेत्रे (उदा., विद्युत् चुंबकीय) ही मूलभूतपणे पुंज स्वरूपाचीच असतात व सूक्ष्म स्तरावर होणाऱ्या घटनांचे वर्णन करण्याकरिता त्यांच्या पुंज आविष्काराच्या उपयोग करावाच लागतो पण स्थूलमानी घटनांचा विचार करताना त्याकरिता (किंवा जर क्षेत्राची तीव्रता कमी असेल तर) रूढ क्षेत्रासाठी यथार्थ असे गणितकृत्य केल्यास त्यामुळे फारशी चूक होत नाही. परस्परक्रिया करणाऱ्या मूलकणांमध्ये असलेले अंतर जेव्हा सूक्ष्म प्रमाणाचे असते तेव्हाच ही क्षेत्रे आपले विशिष्ट व चमत्कारिक गुणधर्म दाखवितात. रूढ क्षेत्रांचा शोध अगोदर लागला असल्यामुळे त्यांविषयींची कल्पना करणे आपणांस सोपे ठरते. म्हणून सुरुवातीस या रूढ प्रकारच्या क्षेत्रांविषयी विचार करणे योग्य ठरेल. रिक्त अवकाशातील प्रत्येक बिंदूजवळ जेव्हा एक प्रकारचा तणाव किंवा प्रतिबल आहे असा अनुभव येतो तेव्हा त्या अवकाशात क्षेत्र आहे असे म्हणतात. ज्या ठिकाणी क्षेत्र आहे अशा ठिकाणी एक द्राव्यिक वस्तू ठेवली, तर तिच्यावर या क्षेत्रामुळे प्रेरणा मिळते. या प्रेरणेमुळे वस्तू गतिमान होते. या प्रेरणेच्या अस्तित्वानेच (किंवा तेथे ठेवलेल्या वस्तूच्या गतीमुळे) या ठिकाणी क्षेत्र आहे असे दाखविता येते. निर्वातामध्ये एकमेकांपासून काही अंतरावर दोन एकाच प्रकारच्या विद्युत् भारांचे कण ठेवले असता त्यांमध्ये जे प्रतिसारण होते (किंवा त्यांवर जी प्रेरणा आढळते) तिची मीमांसा विद्युत् क्षेत्र गृहीत धरून दिली जाते. पहिल्या विद्युत् भारित कणामुळे त्याच्या सभोवतालच्या परिसरात प्रथम विद्युत् क्षेत्र निर्माण होते. ज्या ठिकाणी दुसरा विद्युत् भारित कण असेल त्या ठिकाणी निर्माण झालेले स्थानिक विद्युत् क्षेत्र त्या कणावर कार्य करून मग त्यावर प्रतिसारक प्रेरणा निर्माण करते. या विशदीकरणामध्ये प्रतिसारक प्रेरणेचे मूळ, दुसरा विद्युत् भारित कण व त्या स्थानिक जागी असणारे विद्युत् क्षेत्र यांच्या परस्परक्रियेत आहे असे मानलेले असते. वर गृहीत धरलेले कण स्थिर नसून त्यांना एकमेकांच्या सापेक्ष गती असतील, तर विद्युत् व चुंबकीय या दोन्ही प्रकारची क्षेत्रे त्यांवर एकाच वेळी कार्य करताना आढळतात. विद्युत् चुंबकीय क्षेत्रे विद्युत् भारित कणाच्या गतीतच बदल घडवून आणतात असे नसून, काही परिस्थितीत एक प्रकारचे क्षेत्र दुसऱ्या प्रकारच्या क्षेत्रात बदल घडवून आणू शकते. कालानुसार बदलणारे विद्युत् क्षेत्र चुंबकीय क्षेत्र निर्माण करू शकते, तर बदलते चुंबकीय क्षेत्र विद्युत् क्षेत्र उत्पन्न करू शकते हे प्रयोगाने दाखविता येते. याचा खुलासा मूलभूत मॅक्सवेल विद्युत् चुंबकीय समीकरणांमध्ये अंतर्भूत केला आहे [→ मॅक्सवेल विद्युत् चुंबकीय समीकरणे].
न्यूटन यांच्या यामिकीत(प्रेरणांची वस्तूंवर क्रिया आणि त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रात) गृहीत धरलेल्या द्रव्यकणाइतकेच या क्षेत्रांना स्वतंत्र व वास्तविक अस्तित्व आहे, हे प्रथम शास्त्राज्ञांच्या लक्षात आले नाही. त्यामुळे सुरुवातीच्या काळात विद्युत् चुंबकीय क्षेत्राकरिता वाहक म्हणून ‘ईथर’ या नावाचे कल्पित असे माध्यम गृहीत धरण्यात आले होते[→ ईथर–२] काही परिस्थितीत विद्युत् चुंबकीय तरंग (उदा., प्रकाश, रेडिओ तरंग) उत्सर्जित करता येतात ते ईथरमध्येच निर्माण केले जातात असे विवेचन केले जात असे. सध्याच्या कल्पनेप्रमाणे विद्युत् चुंबकीय क्षेत्राला आधारभुत किंवा तरंगांना वाहक म्हणून कोणत्याही माध्यमाची आवश्यकता असत नाही. ही कल्पना ॲल्बर्ट आइनस्टाइन(१८७९–१९५५) यांनी आपल्या सापेक्षता सिद्धांतामध्ये प्रथम मांडली. क्षेत्रामध्ये असलेल्या कणाइतकेच हे क्षेत्र वास्तविक आहे, असे सध्या समजले जाते. प्रसारित केलेले विद्युत् चुंबकीय तरंग म्हणजेच उत्सर्जित केलेली विद्युत् चुंबकीय क्षेत्रे होत. अशा रीतीने उत्सर्जित केलेली क्षेत्रे कोणत्याही विद्युत् भारित कणसमूहाशी निगडित नसतात व ती स्वतंत्रपणे अवकाशातून प्रगत पावतात, यावरून क्षेत्रांना स्वतंत्र अस्तित्व आहे असे म्हणता येते. विद्युत् व चुंबकीय क्षेत्रे यांना फक्त विद्युत् भार अथवा चुंबक यांच्या सन्निधच अस्तित्व असेत असे नसुन ते कोणत्याही प्रत्यक्ष द्रव्यरूप वस्तूच्या अनुउपस्थितीत सुद्धा– म्हणजेच निर्वातामध्ये सुद्धा– मिळू शकते. चल (गतिमान) विद्युत् भारित कणांमधील परस्परक्रियेचा विचार करताना विद्युत् चुंबकिय विक्षोभ (क्षेत्रामधील कालपरत्वे पडणारा फऱक) हा प्रकाशाच्या ठराविक वेगाने प्रसारित होतो हे लक्षात घ्यावे लागते. या कारणाकरिता प्रत्यक्ष क्षेत्र आणि विद्युत् भारित कण यांमध्ये ऊर्जेची व संवेगाची (द्रव्यमान व वेग यांच्या गुणाकाराने मिळणाऱ्या भौतिकिय राशीची) देवघेव होत असले पाहिजे, असे दाखविता येते.
क्षेत्रामध्ये एका स्थानी असलेल्या विद्युत् भारित कणाच्या ऊर्जेत व संवेगात जर लावलेल्या विद्युत् क्षेत्रामुळे काही फरक झाला (प्रेरणेमुळे कणाच्या गतीत बदल झाल्यास त्याची ऊर्जा व संवेग या दोहोंत बदल होईल), तर ऊर्जा व संवेग अक्षय्यता नियमानुसार [→ द्रव्य आणि ऊर्जा यांची अक्षय्यतासंवेगाची अक्षय्यता] तेवढाच फरक प्रतिक्रियेच्या स्वरूपात त्या कणापाशी असलेल्या स्थानिक क्षेत्रामध्ये झाला पाहीजे हे उघड आहे. विद्युत् चुंबकीय विक्षोभ प्रसारणाचा वेग अनंत नसल्यामुळे, ज्यामुळे हे क्षेत्र निर्माण झाले आहे अशा विद्युत् भारित कणसमूहापर्यंत, हा संवेग आणि ऊर्जा यांमधील फऱक पोहचावयास काहीतरी ठराविक कालावधी लागतो. मूळ विद्युत् भारित कणाच्या ऊर्जा व संवेग यांमधील बदल प्रतिक्रियेच्या स्वरूपात या कणसमूहापर्यंत ताबडतोब पोहोचू शकत नाही. याकरिता परस्परक्रिया चलकण व क्षेत्र यांमध्येच प्रथम होते असे मानण्याशिवाय गत्यंतर राहत नाही. वरील न्यूटन यांच्या यामिकीत विवेचनावरून विद्युत् चुंबकीय क्षेत्रास सुद्धा ऊर्जा व संवेग असल्यामुळे, या क्षेत्राचे वर्णन भौतिकीय प्रणाली अथवा कण यांकरिता वापरण्यात येणाऱ्या गणितीय पद्धतीने करता येईल हे स्पष्ट होते. रूढ भौतिकिप्रमाणे हे एक द्रायूसारखे (वायू अथवा द्रव पदार्थासारखे) अखंड माध्येम आहे व त्याचे अवकाशात समवितरण केले जाते. पुंज क्षेत्र सिद्धांताप्रमाणे या क्षेत्राला कणसद्दश गुणधर्म असतात. सूक्ष्म स्तरांतील आविष्काराचे विशदीकरण करण्याकरिता कणाच्या काही राशींचे पुंजीकरण करावे लागते [उदा., नील्स बोर यांच्या मींमासेप्रमाणे अणूमधील इलेक्ट्रॉनांना (कणांना) काही विशिष्ट पृथक् ऊर्जा मूल्येच धारण करता येतात असे आढळते याचा अर्थ असा होतो की, इलेक्ट्रॉन ऊर्जेचे पुजीकरण करणे आवश्यक ठरते]. याच न्यायाने क्षेत्राच्या काही राशींचे (उदा., ऊर्जा) पुंजीकरण आवश्यक ठरते. न्यूटनच्या गतिकी शास्त्रात कणाची ऊर्जा किंवा संवेग बदलता येतो पण प्रत्यक्ष कणाची निर्मीती अथवा विनाश या विक्रिया होत नाहीत. पुंज क्षेत्र सिद्धांतामध्ये क्षेत्र-पुंजाची निर्मीती अथवा विनाश या क्रियांचाही विचार करता येतो. उदा., इलेक्ट्रॉनाला ऊर्जा पुरविली असता त्यापासून विद्युत् चुंबकीय क्षेत्रपुंजाची म्हणजे फोटॉनाची निर्मीती होते. याउलट फोटॉनचे शोषण झाले असता त्यांचा विनाश होतो. अशा रीतीने या सिद्धांतामुळे द्राव्यिक सृष्टीची कशी उत्पत्ती झाली असावी, या मूलभूत प्रश्नांवर प्रकाश पडतो.
विद्युत् चुंबकीय क्षेत्राचे संपुर्ण ज्ञान होण्याकरिता या क्षेत्राने व्यापलेल्या अवकाशातील प्रत्येक बिंदूजवळ विद्युत् स्थितिक (स्थिर विद्युत् भारांमुळे निर्माण झालेल्या) व चुंबकीय क्षेत्राचे त्या ठिकाणी असणारे प्रत्येकी मूल्य आणि दिशा अशा एकंदर चार राशी माहीत असावयास पाहिजेत. विद्युत् स्थितिक क्षेत्रांविषयीचे ज्ञान त्या ठिकाणचे अदिश वर्चस‌् फलन माहीत असल्यास मिळते, तर चुंबकीय क्षेत्रांविषयीची संपूर्ण माहिती त्या ठिकाणच्या सदिश वर्चस‌् फलनावरून मिळू शकते.[→ मॅक्सवेल विद्युत् चुंबकिय समीकरण]. अवकाशात अनंत बिंदू असल्यामुळे विद्युत् चुंबकीय (अथवा इतर) क्षेंत्राविषयी संपूर्ण माहिती मिळण्याकरिता एका अनंत चल राशींचा संच माहित असावा लागतो. दुसऱ्या शब्दात याच परिस्थितीचे वर्णन करावयाचे असेल, तर असे म्हणता येते की, क्षेत्र हे एखाद्या अनंत मुक्तता मात्रा असणाऱ्या भौतिकीय प्रणालीप्रमाणे आहे. प्रणालीच्या शक्य असलेल्या परिवर्तनाच्या प्रकारची संख्या मुक्तता मात्रांमुळे दर्शविली जाते (सरळ स्प्रिंगेला खालीवर अशी एका प्रकारचीच गती अथवा एकच मुक्तता मात्रा असते, तर साध्या लंबकाच्या मुक्ता मात्रांची संख्या तीन असते.
विद्युत् चुंबकिय क्षेत्र पुंजाचा शोध पुंज परस्परक्रिया : कृष्ण पदार्थापासून [सर्वच्या सर्व आपाती प्रारण–तरंगरूपी ऊर्जा-शोषून घेणाऱ्या व तापविला असता संपूर्ण प्रारण उत्सर्जित करणाऱ्या आदर्श व काल्पनिक पदार्थापासून→कृष्ण पदार्थ] बाहेर पडणाऱ्या विद्युत् चुंबकीय प्रारणातील ऊर्जा वितरणाची उपपत्ती लावण्याचे प्रयत्न माक्स प्लांक यांनी १९०० साली केले तेव्हा विद्युत् चुंबकीय क्षेत्राच्या पुंजीकरणाचा शोध लावला. या सिद्धाताप्रमाणे[→ पुंज सिद्धांत] प्रारणाचे उत्सर्जन किंवा शोषण होते तेव्हा त्याची क्षेत्रीय ऊर्जा या एककाच्या पूर्ण पटीतच बदलते (h= प्लांक v = प्रारण कंप्रता –म्हणजे दर सेकंदाला होणाऱ्या कंपनांची संख्या) यानंतर १९०५ साली आइनस्टाइन यांनी प्रकाशविद्युत् परिणामाचे [→ प्रकाशविद्युत्] विशदीकरण करण्याकरिता प्रकाश क्षेत्र( विद्युत् चुंबकीय क्षेत्र) ऊर्जा हीसुद्धा पुंजकणांची बनली आहे हा सिद्धांत मांडला. या कल्पनेप्रमाणे विद्युत् चुंबकीय (प्रारण) क्षेत्र हे फोटॉन या मुलभूत कणाचे बनलेले असून फोटॉनाची ऊर्जा तर त्याचा संवेग एवढा असतो. फोटॉनाचे शून्यगती- द्रव्यमान शून्य असते. [→ फोटॉन].
व्यतिकरण, विवर्तन यांसारख्या आविष्कारांत [→ प्रकाशकी] तरंग स्वरूप तर प्रकाशविद्युत् इ. आविष्कारांत कण स्वरूप दाखविणारा फोटॉन हा पहीलाच मूलकण होय. त्यामुळे त्यास विद्युत् चुंबकीय क्षेत्राच्या वाहक अशी संज्ञा दिली जाते. ऊर्जा व द्रव्यमान .यांमध्ये परस्परबदल शक्य असल्यामुळे पुंज क्षेत्र सिद्धांतामध्ये मागे नमूद केल्याप्रमाणे कणांच्या परस्परक्रियेत पुंजकणांची (मूलकणाची)निर्मिती व विनाश या क्रियांचा अंतर्भाव होतो. रूढ भौतिकीप्रमाणे कोणताही विद्युत् भारित कण प्रवेगित झाल्यास त्याच्या पासून फोटॉनाचे उत्सर्जन (निर्मिती) होऊ शकते. इलेक्ट्रॉन हा सर्वांत हलका कण असल्यामुळे प्रत्यक्षात त्याव्दारे फोटॉनाचे उत्सर्जन व शोषण या क्रिया सहज घडून येतात (बोर यांच्या मीमांसाप्रमाणे अणूमधील बंधित इलेक्ट्रॉनाला योग्य ऊर्जा मिळल्यास तो तिचे शोषण करूण शेवटी फोटॉनाचे उत्सर्जन करू शकतो). पुंज क्षेत्र सिद्धांताप्रमाणे दोन विद्युत् भारित कणांमधील परस्परक्रियेचे विशदीकरण क्षेत्र पुंजकणाचे (फोटॉनचे) छद्वा उत्सर्जन व शोषण या दोन कणांव्दारे होते असे कल्पून केले आहे. या विवेचनानुसार प्रत्येक परस्परक्रियेबरोबर ठराविक अवकाशस्थानी व काळी क्षेत्र पुंजकणाची निर्मिती किंवा विनाश या क्रिया निगडित असतात, हे विधान आ.१ वरून स्पष्ट होईल.
या आकृतीमध्ये दोन वेगवान इलेक्ट्रॉनांमधील परस्परक्रियेची काही अंगे आर‌्.पी. फाइनमन यांच्या पद्धतीने दाखविली आहेत. यामध्ये दोन इलेक्ट्रॉन (१) व (२) एकमेंकाजवळ आल्यामुळे त्यांमध्ये प्रतिसारणी प्रेरणा कार्यान्वित होऊन त्यामुळे ते शेवटी एकमेकांपासून जास्त दूर जातात, असे रूढ विशदीकरण देता येते. पुंज क्षेत्र सिद्धांताप्रमाणे इलेक्ट्रॉन (१) हा अ या ठिकाणी एक छद्य फोटॉन उत्सर्जित करतो. त्यामुळे त्याच्या गतिदिशेत बदल होतो व याच ठिकाणी पुंजकणाची निर्मिती होते. इलोक्ट्रॉन (२) आ या ठिकाणी फोटॉनाचे शोषण करतो त्यामुळे त्या ठिकाणी त्याच्या गतिदिशेत बदल होतो. आ या ठिकाणी पुंजकणांचा नाश होतो. वरील परस्परक्रियेत छद्य फोटॉनाचे उत्स्फूर्त व शोषण या क्रिया मूलभूत आहेत. अशा प्रकारे जेव्हा फोटॉनचे उत्सर्जन होते तेव्हा उत्सर्जित फोटॉन काही ऊर्जा घेऊनच बाहेर पडतो पण ही ऊर्जा मूळ प्रणालीपासून (म्हणजे इलेक्ट्रॉनांपासून) घेतली जात नसल्यामुळे सर्व प्रणालीची एकंदर ऊर्जा वाढली असा भासमान समज होतो. या परिस्थितीत ऊर्जेच्या अक्षय्यता नियमाचे उल्लंघन होते असे वाटेल. पुंज क्षेत्र सिद्धांताप्रमाणे असे गृहीत धरलेले असते की, फोटॉनाचे छद्य उत्सर्जन व शोषण एकमेकांनंतर इतक्या त्वरेने होते की फोटॉन उत्सर्जनामुळे होणाऱ्या उर्जेतील वाढीचे प्रयोगाने निरीक्षण करता येत नाही. याचाच अर्थ असा होतो की, अशा ऊस्फूर्त रीतीने ऊत्सर्जित होणाऱ्या फोटॉनाचे सुद्धा निरीक्षण करता येत नाही.
इलेक्ट्रॉनाला बाहेरून ऊर्जा पुरवून त्याला प्रवेगित केले असता त्यापासून जे फोटॉन उत्सर्जित होतात ते मात्र वास्तव असतात व त्यांचे प्रयोगाने निरीक्षण करता येते. पहिल्या वर्णनामध्ये दिलेल्या दूर अंतरावरून सिद्ध होणाऱ्या एका परस्परक्रियेऐवजी आधुनिक सिद्धाताप्रमाणे दोन स्थानिक परस्परक्रिया गृहीत धरल्या आहेत. यामध्ये गृहीत धरलेले फोटॉनाचे उत्सर्जन व शोषण छद्य स्वरूपाचे असते असे समजले जाते.
या सिद्धांताप्रमाणे परस्परक्रिया कार्यान्वित होण्याचा वेग प्रकाशवेग c एवढा आहे, ही महत्त्वाची माहीती मिळते. या सिद्धांताच्या आधारे इलेक्ट्रॉन आणि विद्युत् चुंबकीय क्षेत्र (स्वनिर्मित वा इतर) यांमधील परस्परक्रिया इलेक्ट्रॉन-पॉझिट्रॉन युग्म निर्मिती अथवा नष्टीकरण इ. मूलभूत प्रश्न यशस्वी रीतीने सोडविता येतात.
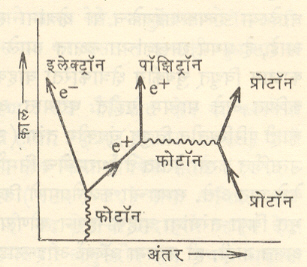
या सिद्धांताच्या साहाय्याने काढलेले निष्कर्ष व प्रयोगाने मिळणारे निष्कर्ष यांमध्ये एकवाक्यता दिसून येते, आ. २ मध्ये एका प्रोटॉनाच्या उपस्थितीत एका फोटॉनापासून इलेक्ट्रॉन- पॉझिट्रॉन युग्माची निर्मिती कशी होते हे फाइनमन आकृतीव्दारा दाखविले आहे. या आकृतीवरून निर्माण झालेल्या पॉझिट्रॉन एका फोटॉनाचे उत्सर्जन करतो व प्रोटॉन या फोटॉनाचे शोषण करतो हे दिसते. या भौतिकिय प्रक्रियांचे स्पष्ट चित्रण अशा फाइनमन आकृतीवरून मिळते. आकृतीवरून या प्रक्रियेशी संबंधित असलेल्या आव्यूहाचे घटक लिहिता येतात. आकृतीमधील निरनिरळ्या रेषा, शाखा युग्मांची संख्या व शिरोबिंदु( फोटॉन दर्शविणाऱ्या रेषा जेथे संपतात ते बिंदू ) यांवरून कोणते गणितीय कारक वापरायाचे याकरिता नियम उपलब्ध आहेत. फाइनमन आकृतीवरून केवळ गुणात्मक अशी माहिती मिळत नसून तिचा प्रत्यक्ष संख्यात्मक स्वरूपाची माहिती मिळविण्याकरिता उपयोग होतो. पॉझिट्रॉन – इलेक्ट्रॉन युग्मनिर्मिती व नष्टीकरण आणि पॉझिट्रोनियम यांविषयी ‘पॉझिट्रॉन’ ही नोंद पहावी.
विद्युत् चुंबकिय क्षेत्राचे पुंजीकरण : मॅक्सवेल समीकरणांनी ज्याचे वर्णन करता येते असे विद्युत् चुंबकीय मुक्त प्रारण एका आयताकार आवरणआत बंदिस्त केले आहे असे समजू. आवरणातील अवकाशात विद्युत् भार समूह नसल्यामुळे प्ररणाचे स्वरूप मुक्त आहे असे म्हटले जाते. या आवरणाच्या बाजू संपूर्णपणे परावर्तनशील आहेत असे मानल्यामुळे या आवरणामध्ये फक्त स्थिर स्वरूपाचे तरंगच राहू शकतील हे उघड आहे. आवरणाच्या लांबी, रुंदी व उंची या परिमाणांमुळे तरंगरचनेवर काही सीमा अटी पडतील यामुळे काही ठराविक तरंगलांबीचे (कंप्रतेचेच) तरंग स्थिर स्थितीत आवरणामध्ये मिळतात. तरंगविज्ञानाचा आधार घेऊन आवारणात मिळणारी विद्युत् चुंबकीय तरंगाची सर्वांत कमी कंप्रता ही जर मूलभूत कंप्रता मानली, तर या कंप्रतेच्या गुणित (पटीत असणाऱ्या) कंप्रताच फक्त
या आवरणात उपस्थित राहू शकतात असे कळते. मूलभूत कंप्रता घटकव गुणित कंप्रता घटक यांचे परमप्रसर (आवर्तनातील महत्तम स्थानांतरणे) माहीत असतील, तर अध्यारोपण तत्त्वाचा उपयोग करून एकंदर दोलायमान विद्युत् चुंबकीय प्रारण क्षेत्राच्या परमप्रसराचे अवकाश वितरण काढता येते. गणितीय दृष्ट्या यामधील प्रत्येक कंप्रता घटक एका हरात्मक (एकाच कंप्रतेच्या) आंदोलकाच्या (जिच्या समतोलाच्या भंग झाला असता स्थानांतराशी समप्रमाणात असणाऱ्या एका पुनःस्थापक प्रेरणेमुळे जिला आंदोलक गती प्राप्त होते अशा भौतिक प्रणालीच्या) समतुल्य आहे, असे समजता येते. अशा रीतीने संपूर्ण विद्युत् चुंबकीय प्रारण क्षेत्राचे संख्यात्मक वर्णन, त्याला समतुल्य असलेल्या सर्व हरात्मक आंदोलकाचा एकत्र विचार करून देता येते. पुंज सिद्धांताप्रमाणे हरात्मक आंदोलकाच्या ऊर्जेचे पुंजीकरण करावे लागते. त्याची ऊर्जा काही पृथक् विशिष्ट मूल्येचे धारण करू शकते. ऊर्जेची ही मूल्ये सुत्राने मिळतात [→ पुंजयामिकी]. येथे h=प्लांक स्थिरांक, v= आंदोलक कंप्रता, n= पूर्णांक. यावरून या आंदोलकांना समतुल्य असलेल्या विद्युत् चुंबकीय क्षेत्राच्या ऊर्जेची याचप्रमाणे पुंजीकरण करणे आवश्यक आहे असे दाखविता येते. क्षेत्राच्या अनेक घटकांपैकी एका घटकाची ऊर्जा असेल, तर क्षेत्राकरिता वरील सुत्राचा असा अर्थ होतो की, या स्थितीत hv ऊर्जा असलेले n फोटॉन क्षेत्रांमध्ये उपस्थित आहेत. आवरणात अनुज्ञात असलेल्या सर्व कंप्रतांचा विचार केल्यास क्षेत्राची संपूर्ण ऊर्जा या सूत्राने मिळते. आयताकार आवरणाकरिता k=३ होईल. कोणत्याही एका कंप्रतेकरिता मिळणारी क्षेत्र ऊर्जा जेव्हा पुंज नियमानुसार पृथक् रीत्या बदलते(हा बदल मध्ये बदल झाल्यामुळे होणार) तेव्हा त्या तऱ्हेच्या फोटॉनांच्या संख्येत बदल होतो. फोटॉन ऊत्सर्जन (निर्मिती) किंवा शोषण (विनाश) झाल्यामुळे हा बदल घडून येतो. आवरणातील सर्व कंप्रताचे फोटॉन विनाश पावले तर बंदिस्त अवकाशात फोटॉन राहणार नाहीत अशा परिस्थितीत म्हणजे निर्वावातील क्षेत्राची ऊर्जा शून्य नसून तिचे मुल्य एवढे राहते. यावरून फोटॉन नसले, तरी क्षेत्राला अस्तित्व आहे असा आश्चर्यकारक निष्कर्ष मिळतो. या उर्जेचे मूळ → अनिश्चितता तत्त्वात आहे, असे दाखविता येते. पुंज सिद्धांताप्रमाणे हरात्मक आंदोलकांची लघुत्तम ऊर्जा शून्य नसून hv एवढी असते या निष्कर्षाशी वरील निष्कर्ष सुसंगत असा आहे. क्षेत्राच्या ऊर्जेचे पुंजीकरण केल्यामुळे वरील किमान ऊर्जा उरते. यामुळे मिळणारे काही निष्कर्ष प्रयोगाने पडताळून पहाता येतात. उदा., जर दोन निर्भारित समांतर विद्युत् वाहक एकमेंकाजवळ आणली(अंतर=d), तर त्यांमध्ये F= एवढी आकर्षण प्रेरणा मिळेल असे दाखविता येते (A=प्रतल क्षेत्रफळ, h=प्लांक स्थिरांक, C=प्रकाशवेग). प्रत्यक्ष प्रयोगाने मिळलेल्या प्रेरणेचे मूल्य वरील सूत्रांनी दिलेल्या मूल्याशी जूळते. लँब स्थानच्युती हा दुसरा परिणाम विद्युत् चुंबकीय क्षेत्राच्या पुंमजीकरणामुळे मिळतो. [→पुंजयामिकी].
विविध मूलभूत परस्परक्रिया व तदनुरूप क्षेत्रे : आतापर्यंतचे विवेचन मुख्यत्वेकरून विद्युत् चुंबकीय परस्परक्रिया (व क्षेत्र) यांच्या आधारे करण्यात आले आहे. भौतिकीत मुख्यत्वेकरून कोष्टक क्र. १ मध्ये दिलेल्या चार प्रकारच्या परस्परक्रिया (अथवा क्षेत्रे) आढळतात आणि कोष्टकात दिलेली सामर्थ्य सापेक्षा प्रमाणाची मूल्ये एका विशिष्ट मूल्य गणनानुसार मिळालेली आहेत.
ज्यामध्ये विद्युत् चुंबकीय परस्परक्रियेचे विशदीकरण त्या क्षेत्राच्या फोटॉन या पुंजकणाच्या छद्मं उत्सर्जन व शोषण या प्रक्रियेच्या साहाय्याने करतात, त्याच प्रमाणे प्रत्येक प्रकारच्या परस्परक्रियेकरिता एक विशिष्ट क्षेत्र व त्याकरिता असणारा विशिष्ट क्षेत्र पुंजकण गृहीत धरलेला असतो. क्षेत्राचे पुंजीकरण केल्यामुळे हा पुंजकण मिळतो. क्षेत्र पुंजकणाच्या द्रव्यमानानुसार तदनुरूप परस्परक्रियेचा पल्ला निश्चित होतो. जेवढा पल्ला मोठा तेवढे पुंजकणांचे द्रव्यमान कमी असते. कोष्टक क्र. १ मध्ये परस्परक्रिया व क्षेत्र प्रकारचे वर्णन, त्या क्रियेच्या सामर्थ्याचे सापेक्ष प्रमाण, तिचा पल्ला, त्याकरिता उपयोगात आणला जाणारा क्षेत्र पुंजकण यांची माहिती दिली आहे. येथे नमूद केले पाहिजे की, फोटॉन किंवा मेसॉन हे पुंजकण प्रत्यक्ष अथवा अप्रत्यक्ष रीतीने प्रयोगशाळेत संशोधिले गेले आहेत. ग्रॅव्हिटॉन व मध्यस्थ बोसॉन या पुंजकणांच्या अस्तित्वाबद्दल अद्यापपावेतो प्रत्यक्ष अथवा अप्रत्यक्ष पुरावा उपलब्ध नाही. परस्परक्रियांच्या सापेक्ष तीव्रतांवरून व त्यांच्या पल्लांवरून (३) व (४) या क्रियांना अनुक्रमे दुर्बल अणूकेंद्रीय व प्रबल अणूकेंद्रीय परस्परक्रिया का म्हणतात याचा खुलासा होतो. वर जरी परस्परक्रियांचे चारच प्रकार वर्णिली असले, तरी यांशिवाय आणखी इतर प्रकारच्या परस्परक्रिया असण्याची शक्यता नाकारता येणार नाही. दुर्बल अणूकेंद्रीय परस्परक्रियेच्या (क्षेत्राच्या) साहाय्याने किरणोत्सर्गी अणूच्या बीटा क्षयाचे विवेचन एन्रीको फेर्मी यांनी दिले [→ किरणोत्सर्ग].
दुर्बल अणुकेंद्रीय व विद्युत् चुंबकीय परस्परक्रिया यांमधील परस्परसंबंध : उच्च ऊर्जा भौतिकीमध्ये झालेल्या काही घडांमोडींवरून दुर्बल अणूकेंद्रीय परस्परक्रियेच्या स्वरूपाविषयी अधिक माहिती उपलब्ध झाली आहे. न्यूट्रॉन, म्यूऑन, पायॉन, केऑन व हायपरॉन यांसारख्या मुलकणांच्या ऱ्हास दुर्बल परस्परक्रियेमुळे होतो. दुर्बल व विद्युत् चुंबकीय परस्परक्रिया या दोन्ही गेज(मापक) परस्परक्रिया या नावाने ज्ञात असलेल्या अधिक व्यापक स्वरूपाच्या क्रियेने दोन विशिष्ट प्रकार असावेत, असा समज होण्याइतका प्रायोगिक पुरावा उपलब्ध झाला आहे. या व्यापक परस्परक्रियेचे सैद्धांतिक संशोधन एस‌्. वाइनबर्ग व ए. सलाम यांनी केले आहे. विद्युत् चुंबकीय व दुर्बल परस्परक्रिया यांची मूलभूत स्वरूपे आ. ३, ४ व ५ यांवरून स्पष्ट होतील.
कोष्टक क्र.१. विविध मूलभूत परस्परक्रिया अथवा क्षेत्रे व त्यांचे गुणधर्म
| परस्परक्रिया अथवा क्षेत्रप्रकार | सामर्थ्याचे सापेक्ष प्रमाण | कार्यकारी पल्ला | क्षेत्र पुंजकण | सरासरी आयुष्य ( सेकंद) | निसर्गातील प्रमुख कार्य | |
| १. | गुरुत्वीय | १० – ३९ | मोठा | ग्रॅव्हिटॉन* | अनंत | द्रव्य बंधनक्रियेमुळे तारे व
दीर्घिका (तारामंडळे) यांची निर्मिती. |
| २. | विद्युत् चुंबकीय | १० -२ | मोठा | फोटॉन | अनंत | इलेक्ट्रॉन व अणुकेंद्रे यांमधील बंधनक्रियेने अणू व रेणू यांची
निर्मिती आणि अणू व रेणू यांमधील बंधनक्रियेमुळे |
| ३. | दुर्बल अणुकेंद्रीय | <१०-५ | <<१०-१५ सेंमी. बोसॉन* | मध्यस्थ
बोसॉन* |
— | स्थूलमानीय द्रव्याची निर्मिती.
अणुकेंद्रे, न्युट्राॅन व इतर मूलकणांचा ऱ्हास. |
| ४. | प्रबल अणुकेंद्रीय | १ | ~१०-१३ सेमी.मेसॉन (पाय्) | १०-१६ ते १०-८ | १०-१६ ते १०-८ | प्रोटॉन व न्यूट्रॉन यांच्या बंधनाने
अणुकेंद्रांची निर्मिती. |
आधुनिक मीमांसाप्रमाणे न्युट्रॉनचे जेव्हा प्रोट्रॉनामध्ये रूपांतर होते, तेव्हा एक बोसॉन उत्सर्जित केला जातो. विद्युत् भार अक्षय्यता तत्त्वाप्रमाणे यावरील विद्युत् भार ऋण असला पाहिजे, त्याचा परिवलनांक एक व त्याचे द्रव्यमान खूपच मोठे असले पाहिजे. हे निष्कर्ष सैद्धांतिक दृष्ट्या काढता येतात. त्याच्या प्रतिकणावर विद्युत् भार एवढा असला पाहीजे हे दाखविता येते.
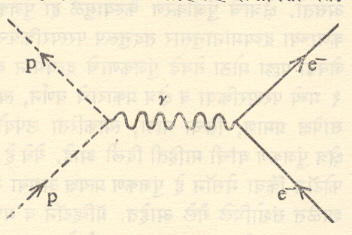
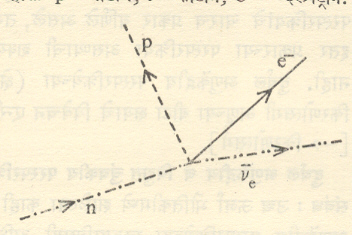
वरील सुलभ विशदीकरणात दोन दोष आहेत असे आढळते. विद्युत् भार अक्षय्यता अट पाळली जात नाही व बोसॉन क्षेत्र हे गेज रूपांतरणाकरिता निश्चल राहत नाही. मीमांसेतील हे दोष घालविण्याकरिता गेज सिद्धांत मांडण्यात आला. या सिद्धांतामध्ये विद्युत् भाराकरिता एक व्यापक अर्थ दिला आहे व यामध्ये दुर्बल आणि विद्युत् चुंबकीय परस्परक्रियांचे मिश्रण करण्यात आले आहे. व्यापक व मिश्रित क्षेत्रांकरिता w बोसॉनाच्या बरोबर शून्य विद्युत् भार असलेल्या z बोसॉनाचाही क्षेत्र पुंजकण म्हणून वापर करण्यात आला आहे. निष्क्रिय z बोसॉनामुळे निर्माण झालेले काही प्रकीर्णन परिणाम जिनीव्हा येथील यूरोपीय उच्च ऊर्जा प्रयोगशाळेत (CERN) १९७३ मध्ये, तर अमेरिकेत स्टॅनफर्ड प्रयोगशाळेत त्याच वर्षी प्रयोगाने सिद्ध केले गेले आहेत. गेज सिद्धांतामध्ये गृहीत धरलेले सर्व प्रकारचे बोसॉन एकमेकांशी परस्परक्रिया करतात व त्यामुळे काही परिस्थितीत त्यांमध्ये अवस्था संक्रमण होणे शक्य होते. या संक्रमणामुळे त्यांच्या व्दारा विद्युत् चुंबकीय व दुर्बल अशा निरनिरळ्या प्रकारच्या परस्परक्रिया घडुन येऊ शकतात.
प्रबल अणुकेंद्रीय अथवा यूकावा क्षेत्र : अणूकेंद्रांत न्यूक्लिऑन (प्रोट्रॉन किंवा न्यूट्रॉन) या प्रकारचेच मूलकण आहेत. अणुकेंद्राची त्रिज्या साधारणपणे या मानाची असल्यामुळे यामधील सर्व कण एकमेकांच्या अगदी जवळ असले पाहिजेत हे उघड आहे. प्रोट्रॉनांवर विद्युत् भार आहे व त्यामुळे त्यांमध्ये विद्युत् चुंबकीय परस्परक्रिया होऊन त्यांमध्ये प्रतिसारणी प्रेरणा अस्तित्वात असते. या प्रतिसारणी प्रेरणेवर मात करून अणुकेंद्रातील प्रोट्रॉन एकमेकांबरोबर बंधित अवस्थेत राहतात. यांवरून त्यांमध्ये दुसरी एक जास्त प्रबल अशी आकर्षण प्रेरणा कार्य करित असली पाहीजे हे उघड आहे. ही आकर्षण प्रेरणा प्रोट्रॉन या विद्युत् भारित मूलकणांमध्येच सापडते असे नसून ती प्रोट्रॉन व न्यूट्रॉन किंवा न्यूट्रॉन व न्यूट्रॉन यांमध्ये सुद्धा मिळते. ही प्रेरणा कणाच्या विद्युत् भारावर अवलंबून असत नाही.
हीडेकी यूकावा यांनी १९३५ मध्ये या प्रबल अणुकेंद्रीय परस्परक्रियेचे प्रथम विशदीकरण केले. प्रयोगाने असे आढळले होते की, किंवा यापेक्षा कमी अंतराकरीता ही परस्परक्रिया मिळते. विद्युत् चुंबकीय क्षेत्रजन्य प्रेरणेपेक्षा या परस्परक्रियेचा पल्ला खूपच कमी आहे. यूकावा यांनी या क्रियेकरिता एक विशिष्ट क्षेत्र गृहात धरले. या क्षेत्राचे पुंजीकरण करून ही परस्परक्रिया मेसॉन या पुंजकणाच्या देवघेवीमुळे होते असे मानले. मेसॉनाचे द्रवमान जर असेल, तर त्याचे उत्सर्जन करण्यासाठी एवढी ऊर्जा मूलकणापासून बाहेर पडली पाहिजे. अनिश्चितता तत्त्वाप्रमाणे त्यामुळे या कालखंडात मेसॉन c वेगाने जात असेल, तर एवढे अंतर तो चालून जाईल. हे अंतर जर एवढे असावयास पाहिजे असेल,तर मेसॉनाचे द्रव्यामान असे दाखविता येते. १९३८ साली प्रयोगशाळेत प्रथम सापडलेला म्यू-मेसॉन किंवा म्यूआॅन हाच यूकावा क्षेत्र पुंजकण असावा असे चुकीने समजले गेले पण नंतर खरा पाय-मेसॉन हा १९४८ साली सापडला.यूकावा मेसॉनालाच पायॉन असे म्हणतात. अशा प्रकारचे तीन पायॉन सापडले आहेत. यांपैकी व यांचे द्रव्यमान सारखे असून त्यांचे सरासरी आयुष्यमान सेंकद एवढे आहे. याउलट या पायॉनाचे द्रव्यमान मात्र थोडेसेच कमी असून त्याचे सरासरी आयुष्यमान मात्र खूपच कमी म्हणजे एवढे आहे. मेसॉन हे दुर्बल परस्परक्रियेने इलेक्ट्रॉन (अथवा म्यूऑन) व न्यूट्रिनो (किंवा प्रतिन्यूट्रिनो) या मूलकणांत विघ़टन पावतात.
मुक्त मेसॉनाचे गुणधर्म अथवा वर्तणूक सैद्धांतिक दृष्ट्या चांगल्या रीतीने विशद करता येत असली, तरी त्याच्या इतर न्यूक्लिऑनांबरोबर होणाऱ्या परस्परक्रियांचे विवेचन विशेष समाधानाकारक तऱ्हेने करता येत नाही. या कार्याकरिता लागणाऱ्या क्षेत्र समीकरणांच्या स्वरूपाविषयी निश्चित माहिती नाही. या समीकरणाला मुळात निश्चित निर्वाह आहे की नाही, याविषयीच शंका आहेत.
गुरुत्वीय क्षेत्र अथवा परस्परक्रिया : विद्युत् चुंबकिय क्षेत्रात घडणाऱ्या घटनेच्या सद्दश म्हणून असे मानता येते की, जेव्हा द्रव्यमान प्रवेगित होते तेव्हा त्याच्यापासून गुरुत्वीय प्रारण उत्सर्जित होते. या प्रारणाचे पुंजीकरण केले, तर त्यापासून क्षेत्र पुंजकण ग्रॅव्हिटॉन मिळतो. ग्रॅव्हिटॉनाचे शून्यगती- द्रव्यमान शून्य असून त्यावर विद्युत् भार असत नाही. परिवलन गतीमुळे त्यास एवढा कोनीय संवेग असतो विद्युत् चुंबकीय क्षेत्र आविष्काराचे विवेचन जसे पुंजयामिकीच्या साहाय्याने केले गेले आहे, तशा प्रकारचा प्रयत्न गुरुत्वीय क्षेत्राच्या बाबतीत विशेष प्रगत य़शस्वी झालेला नाही. या क्षेत्राकडे दुर्लक्ष होण्याचे एक कारण असे की, आणवीय अथवा अणूकेंद्रीय आविष्कार समजून घेण्याकरिता गुरुत्वीय क्षेत्राचा उपयोग होत नाही. कारण या क्षेत्राची तीव्रता इतर क्षेत्राच्या मानाने फारच कमी आहे (कोष्टक क्र.१ पहा). त्याचबरोबर गुरुत्वीय परिणामाचे त्याचबरोबर गुरुत्वीय परिणामाचे पुंजयामिकीच्या साहाय्याने विवेचन करणे अवघड आहे, कारण एकतर गुरुत्वीय क्षेत्र समीकरणे अरेषीय (एका एकापेक्षा जास्त घाताची) असल्यामुळे सोडविण्यास कठीण असतात व दुसरे म्हणजे त्यांमधील सिद्धांताचा संपूर्ण भौतिकीय अर्थ अजूनही योग्य प्रकारे समजलेला नाही. गुरुत्वीय क्षेत्राचा अभ्यास अलिकडेच करण्यात येत आहे, कारण पुंज क्षेत्र सिद्धांतामधील काही समस्यांचे (उदा., इलेक्ट्रॉनाची स्वयंऊर्जा अनंत आहे हा अनाकलनीय निष्कर्ष) निराकारण हे क्षेत्र विचारात घेऊन करता येईल असा अनेकांना विश्वास वाटतो.
काही ताऱ्यांच्या बाबतीत अंतःस्फोट होऊन त्यांचे आकारमान मूळ आकारमानाच्या काही सहस्त्र पटींनी कमी होते. या प्रक्रियेमध्ये ताऱ्याच्या आतील द्रव्याची घनता फार मोठ्या प्रमाणावर वाढते. या उच्च घनतेच्या ताऱ्याकरिता किंवा ज्या ताऱ्यामध्ये आकुंचन काही कारणांमुळे सममित न झाल्यामुळे तारा सर्व बाजूंनी तंतोतंत गोलाकार न राहता त्यामध्ये काही ठिकाणी विलक्षिकतता (म्हणजे काही ठिकाणी आकारात स्थानिक, आकस्मित व खंडित प्रकारचे होणारे बदल) निर्माण होतात, या दोन्ही परिस्थितींत पुंज गुरुत्वीय क्षेत्र परिणाम महत्त्वाचे ठरवित अशी अनेकांची अपेक्षा होती.
सममिती व अक्षय्यता नियम : भौतिकीमध्ये अनेक अक्षय्यता नियम महत्त्वाचे समजले जातात. उदा., द्रव्यमान व ऊर्जा या राशी अक्षय्यता नियम पाळतात. याचा अर्थ असा होतो की, द्रव्यमानाचे (किंवा ऊर्जेची) रूपांतर होऊ शकते पण त्याचा नाश वा निर्मिती होऊ शकणार नाही [→ द्रव्य आणि ऊर्जा यांची अक्षय्यता]. अक्षय्यता नियम प्रत्यक्ष अथवा अप्रत्यक्ष प्रयोगाने मिळलेल्या निष्कर्षांवर आधारित आहेत. विवेचनामध्ये त्यांची यथार्थता गृहीत धरली जाते. कोणत्याही राशीकरिता मांडलेला अक्षय्यता नियम हा ती राशी निसर्गात नेहेमी अचल राहते असे दाखवितो. पुंज क्षेत्र सिद्धांतामध्ये बहुतेक प्रक्रियांत मूलकणांची निर्मिती अथवा विनाश या क्रिया होत असल्यासमुळे या प्रक्रियांमध्ये कोणते अक्षय्यता नियम यथार्थ असतात, हे समजून घेणे आवश्यक असते. अक्षय्यता नियम जर गृहीत धरले, तर मूलकण ज्यामध्ये भाग घेतात अशा विविध प्रतिक्रियांचा अभ्यास करून मूलकणांच्या गुणधर्मांविषयी निश्चित माहिती मिळविणे शक्य होते. फोटॉन या पुंज क्षेत्राचे शून्यगति-द्रव्यमान शून्य असून त्यावर विद्युत् भार नाही, त्याला परिवलन एक एकक आहे, फोटॉनाचे उत्सर्जन व शोषण विद्युत् भारित कणांच्या व्दारे होते इ. निश्चित माहिती या प्रकारे मिळविणे शक्य होते. सममिती तत्त्वाचा उपयोग करून यांपैकी बऱ्याचशा अक्षय्यता नियमांचे समर्थन करता येते. भौतिकीय आविष्काराची सममिती म्हणजे काय असा प्रश्न येथे उद्‌भवतो होतो. याकरिता एच. व्हाइल यांनी दिलेल्या व्याख्येचा उपयोग करता येतो. व्हाइल यांच्या मताप्रमाणे जर एखादी वस्तू सममित असेल, तर आपण तीवर काही क्रिया केल्यानंतर सुद्धा ती पहिल्यासारखीच दिसत राहील. भौतिकीय आविष्काराच्या बाबतीत आपण अशा अनेक क्रिया करू शकतो की, ज्या केल्यानंतर सुध्दा आविष्काराचे मूळ स्वरूप बदलत नाही. अशा परिस्थितीत या भौतिकीय आविष्काराला या क्रियांच्या बाबतबीत सममिती आहे असे म्हटले जाते. अक्षय्यता नियमांचे परिपुर्ण व मर्यादित असे वर्गीकरण करता येते. परिपुर्ण अक्षय्यता नियम सर्व प्रक्रियांत व परस्परक्रियांत यथार्थ असतात, तर याउलट मर्यादित स्वरूपाचे नियम काही ठराविक प्रक्रियांकरिंताच यथार्थ असतात. उदा., ऊर्जा अक्षय्यता नियम सर्व प्रकारच्या परस्परक्रियांत पूर्णत्वाने सत्य असतो, तर समता अक्षय्यता [→ समता] दुर्बल परस्परक्रियेत सत्य असत नाही.
कणाच्या गतिकीचे (प्रेरणा कोणत्या प्रकारे गती निर्माण करते याचा अभ्यास करण्याया शास्त्राचे) न्यूटन यांच्या समीकरणांच्या साहाय्याने विशदीकरण करता येते पण यापेक्षा व्यापकीकृत सहनिर्देशक वापरून मिळणारे जे. एल‌्. लाग्रांझ यांचे समीकरण [→ यामिकी] वापरणे जास्त फायदेशीर ठरते. कोणतीही भौतिकीय प्रणाली अथवा कण याकरिता लाग्रांझ राशी अथवा लाग्रांझीयन L पुढील सूत्राने मिळते.
येथे T=गतिज ऊर्जा व V=स्थितीज ऊर्जा आहेत. लाग्रांझीयन L हे स्थानीय सहनिर्देशक q, वेग q व काल t यांच्या फलनाच्या स्वरूपात देता येते म्हणजेच
थोडाफार फरक करून क्षेत्राकरिता (उदा., विद्युत् चुंबकीय) लाग्रांझीयन निश्चित करता येते. न्यूटन यांच्या गतिकीमध्ये कणाकरिता मिळणारे लाग्रांझीयन हे गॅलिलीओ रूपांतरणाकरिता (स्थानांतरणाकरिता) निश्चल असते, तर विद्युत् चुंबकिय क्षेत्रांकरिता मिळणारे लाग्रांझीयन लोरेण्टस रूपातरणाकरिता निश्चल असते (गॅलिलीओ रूपांतरण व लोरेन्ट‌्स रूपांतरण यांच्या स्पष्टीकरणांसाठी अवकाश-काल व ‘संदर्भव्यूह’ या नोंदी पहाव्यात), म्हणजे हे लाग्रांझीयन सापेक्षकता सिद्धांताची सुसंगत असतो.
भौतिकीतील प्रत्येक अक्षय्यता नियम हा एक विशिष्ट सममिती गुणधर्माशी निगडीत आहे असे दाखविता येते. प्रणालीचे लाग्रांझीयन हे जर संदर्भव्यूहाचा आदिबिंदू पुढे (अथवा मागे) सरकवल्यामुळे बदलत नसेल, तर प्रणालीकरीता रेषीय संवेग अचल आहे, असा निष्कर्ष मिळतो. भौतिकीय दृष्ट्या अवकाश सर्वत्र एकविध (एकसारखे) आहे, असाही याचा अर्थ लावता येतो. कोष्टक क्रं. २ मध्ये लाग्रांझीयनच्या विविध स्थानांतरण किंवा रूपांतरण सममितीमुळे ज्यांकरिता निरनिरळे अक्षय्यता नियम मिळतात, त्यांपैकी काही महत्त्वाच्या राशी उदाहरणादाखल दिलेल्या आहेत. याच कोष्टकात ज्या परस्परक्रियेकरिता हा अक्षय्यता नियम यथार्थ ठरतो तिचा उल्लेख पण केला आहे.
कोष्टक क्र. २. सममिती व अक्षय्यता नियम
| स्थानांतरणाचा प्रकार | अक्षय राशी | परस्परक्रिया |
| अवकाश स्थानांतरण | रेषीय संवेग | सर्व परस्परक्रिया |
| काल स्थानांतरण | ऊर्जा E | सर्व परस्परक्रिया |
| अवकाश वलन | कोनीय संवेग | सर्व परस्परक्रिया |
| अवकाश पर्यसन | समता | दुर्बल परस्परक्रियेला लागू नाही. |
| गेज रुपांतरण | विद्युत् भार | सर्व परस्परक्रिया |
(मूलकणाच्या इतर वरीलसारख्या विशिष्ट राशीबद्दल माहिती मिळविण्याकरिता ‘मूलकण’ ही नोंद पहावी)
अवकाश वलन या स्थानांतरण क्रियेत संदर्भव्यूह X, Y किंवा Z यांपैकी कोणत्याही एका अक्षाभोवती एका ठराविक कोनातून फिरविला आहे असे समजलेले असते. अवकाश पर्यसनामध्ये X= -X, Y = -Y, Z = -Z असे रूपांतरण केलेले असते. विद्युत् चुंबकीय क्षेत्राकरिता अदिश वर्चस‌् व सदिश A असेल व स्थानांतरणानंतर त्यांची मूल्ये अनुक्रमे व A होत असतील, तर गेज रूपांतरणाकरिता पुढील लोरेन्ट‌्स समीकरण यथार्थ असते.
[येथे हे चिन्ह सदिश कारक व सदिश यांचा अदिश गुणाकार दर्शविते → सदिश]. अवकाश स्थानांतरणाप्रमाणे काल स्थानांतरण या क्रियेव्दारे कालाचे एकविधत्व सिध्द होते. अवकाश वलन क्रियेमुळे अवकाशाची समदिक‌्ता दर्शविली जोते. अवकाशाचे गुणधर्म सर्व दिशांत सारखेच आहेत, असाही याचा अर्थ होतो.सममितीचा एक थोडासा निराळा प्रकार असे ज्याचे वर्णन करता येईल अशी पुंज क्षेत्र सिद्धांतामधील एक गोष्ट ही की, यामध्ये येणाऱ्या प्रत्येक मूलकणाकरिता एक प्रतिमूलकण असतोच. मूलकण जर विद्युत् भारित असेल, तर त्याच्या प्रतिकणावरिल विद्युत् भार उलट चिन्हाचा असतो उदा., इलेक्ट्रॉन व पॉझिट्रॉन, प्रोटाॅन व प्रतिप्रोटाॅन. कण व प्रतिकण एकमेकांचा निःपात किंवा नष्टीकरण करू शकतात म्हणून त्यास प्रतिकण ही संज्ञा दिली जाते. कण व प्रतिकणाचे द्रव्यमान मात्र एकच असते. काही मूलकणांच्या बाबतीत मूलकण व प्रतिकण हे एकच असू शकतात, उदा., फोटॉन व्यतिकरणामध्ये एक फोटॉन दुसऱ्या फोटॉनाचा नाश करू शकतो. यावरून या विधानाची यथार्थता पटण्यासारखी आहे.
असापेक्षीय पुंज क्षेत्र सिद्धांत : आतापर्यंतच्या विवेचनात प्रामुख्याने पुंज सिद्धांत व सापेक्षता सिद्धांत यांमधील तत्त्वांचा उपयोग केला गेला आहे, अशा आविष्कारांचा विचार केला होता. असापेक्षीय पुंज क्षेत्र सिद्धांतसुध्दा काही विशिष्ट ठिकाणी उपयोगात आणला गेला आहे. अशा परिस्थितीत गणितीय गणन थोडे सुलभ होते. श्रोंडिजर समीकरण हे असापेक्षीय आहे [→ पुंजयामिकी]. त्याचे पुंजीकरण केल्यास इलेक्ट्रॉन समूहाकरिता यथार्थ असा बहुकण पुंज क्षेत्र सिद्धांत मिळतो. हा सिद्धांत घन पदार्थामध्ये (विशेषत: धातूमध्ये) असलेल्या अनेक इलेक्ट्रॉन समूहांच्या सामुदायिक गुणधर्मांचे वर्णन करण्याकरिता उपयोगी पडतो. या रीतीचा उपयोग करून घन पदार्थातील आयनद्रायू आंदोलने [→ आंदोलने भौतिकी] व नीच तापमानकरिता मिळणारी ⇨ अतिसंवाहकता या दोन आविष्कारांचे विशदीकरण करता येते.
संदर्भ : 1. Feynmann, R. P. Leighton, R. B. Sands, M. The Feynmann Lectures on Physics, 3 vols., Bombay, 1966.
2. Ford, K. W. World of Elementary Particles, New York, 1963.
3. Kompanyets, A. S. Theoretical Physics, Moscow, 1961.
4. Muirhead, H. The Physics of Elementary Particles, Oxford, 1968.
5. Sakurai, J. J. Advanced quantum mechnanics, Reading, Mass., 1967.
6. Schweber, S. S. An Introduction to Relativistic, Quantum Field Theory, New York, 1962.
7. Williams, W. S. C. An Introduction to Elementary Particles, New York, 1961.
ताकवले, रा. गो. चिपळोणकर, व. त्रि.
“