व्यतिकरणमापन : (इंटरफेरॉमेट्री). कंप्रता किंवा तरंगलांबी. एकच किंवा जवळजवळ एकच असलेल्या दोन वा अधिक तरंगांचा संयोग होऊन नवीन तरंग निर्माण होण्याच्या प्रक्रियेला व्यतिकरण म्हणतात. या नवीन निष्पन्न तरंगाचा परमप्रसर हा व्यतिकरण होणाऱ्या तरंगांच्या परमप्रसरांची बेरीज असते. निष्पन्न तरंगाच्या परमप्रसरात अंतर किंवा काल यांनुसार बदल होतो. अशा प्रकारे विद्युत्-चुंबकीय, ध्वनी किंवा पाण्यातील तरंग अथवा कोणताही आवर्ती विक्षोभ (खळबळ) यांचे व्यतिकरण होऊ शकते. मराठी विश्वकोशातील तरंग-गती, ध्वनिकी व प्रकाशकी या नोंदींमध्ये व्यतिकरणाविषयी अधिक माहिती आलेली आहे.
प्रकाशकीय व्यतिकरणमापकांचा अभिकल्प (आराखडा) तयार करणे व त्यांचा उपयोग करणे ही कामे व्यतिकरणमापनात केली जातात. प्रकाशकीय व्यतिकरणमापके ही प्रकाशाच्या द्विशलाका व्यतिकरण व बहुशलाका व्यतिकरण या दोन्हींवर आधारलेली असतात आणि ⇨ मापनविज्ञान व ⇨ वर्णपटविज्ञान या विज्ञानशाखांतील ही अतिशय महत्त्वाची साधने आहेत. अगदी भिन्नभिन्न प्रकारच्या मापनांसाठी व्यतिकरणमापके वापरता येतात. उदा. पृष्ठभागाचा आकार किंवा उंचसखलपणा व्यतिकरणमापकाने २५ नॅनोमीटरहून (१ नॅनोमीटर = १०-९ मी. म्हणजे मीटरच्या अब्जांशाएवढे अंतर) अधिक अचूकतेने ठरविता येतो अथवा युग्मताऱ्यांमधील (परस्परांतील गुरुत्वाकर्षणाच्या बंधनामुळे अवकाशात परस्परांच्या पुरेसे जवळ असलेल्या व त्यांच्या समाईक गुरुत्वमध्याभोवतीच्या कक्षेत फिरणाऱ्या ताऱ्यांच्या जोड्यांमधील) लक्षावधी किमी. अंतर व्यतिकरणमापकाच्या मदतीने काढता येते. वर्णपटविज्ञानामध्ये वर्णपटरेषांची अतिसूक्ष्म रचना निश्चित करण्यासाठी व्यतिकरणमापक वापरता येते. परंपरागत, होलोग्राफिक (स्वलेखनकारी) तसेच स्पेकल (कणीदार) व्यतिकरणमापनांत ⇨ लेसर वापरल्यास अभिसारित (प्रसृत) वस्तूंचे विरूपण, कंपन व बाह्यरेखा यांची मापने करणे शक्य झाले आहे. हे पूर्वी करता येत नव्हते.
व्यतिकरण पट्ट : प्रकाशीय ऊर्जा दोन अगर त्याहून जास्त भागांत विभागून हे भाग वेगवेगळ्या मार्गांनी प्रवास करून त्यांचे परत पुनर्मीलन होऊन व्यतिकरण पट्ट म्हणजे एकाआड एक असलेले प्रकाशित व काळसार पट्टे तयार होतात. शलाकेच्या निरनिराळ्या भागांमधील पथांतरांवरून व्यतिकरण पट्टांचा आकार ठरतो.
व्यतिकरणमापके मूलतः प्रकाशीय पथांतर मोजतात. भूमितीय पथ (किंवा भूमितीय लांबी) गुणिले प्रणमनांक [वक्रीभवनांक : → प्रणमनांकमापन] बरोबर प्रकाशीय पथ असल्याने जेव्हा शलाकेचे दोन्ही भाग एकाच माध्यमातून प्रवास करीत असतील, तेव्हा व्यतिकरणमापकात भूमितीय पथांतराचे मापन होते. भूमितीय पथांतर सारखेच असल्यास व्यतिकरणमापकाने प्रकाशीय पथांतर, पथलांबी आणि प्रणमनांकांतील फरक या तीन राशींचे मापन केले जाते. ही मापने प्रकाशाच्या तरंगलांबीच्या एककात मोजली जात असल्याने ज्या प्रयोगात लांबी (अगर अंतर) मोजली जाते, त्यात तरंगलांबीदेखील मोजली जाईल, हे उघड आहे. व्यतिकरण पट्ट ज्या मोजपट्टीवर काढले जातात ती तरंगलांबीच्या सम प्रमाणात असल्याने व्यतिकरणमापकात लोलकाप्रमाणे, पण अधिक शक्तीने संमिश्र प्रकाशाचे अपस्करण (जटिल तरंगसमूहाचे विविध कंप्रता घटकांत अलगीकरण होण्याची क्रिया) होते म्हणजेच व्यतिकरणमापक वर्णपटदर्शक म्हणूनही वापरता येते.
वरील राशी मोजण्याऐवजी त्यांच्यातील सूक्ष्म फरक मोजण्यासाठी व्यतिकरणमापक अधिक योग्य आहे. वस्तुतः अनेक प्रकारची व्यतिकरणमापके फक्त सूक्ष्म फरकच मोजू शकतात. लुमर पट्टिकेद्वारे वर्णरेषेची सूक्ष्म रचना अभ्यासिता येते परंतु तिची तरंगलांबी मोजता येत नाही. झामँ व्यतिकरणमापकामध्ये प्रणमनांकांतील फरक मोजता येतो पण प्रणमनांक मोजला जात नाही. उच्च विभेदन मापनासाठी [→ विभेदनक्षमता] त्याचप्रमाणे तरंगलांबीच्या काटेकोर सापेक्ष मापनासाठी व्यतिकरणमापकाचा उपयोग केला जातो. जवळच्या दोन तरंगलांबीतील १०-६ तरंगाइतका सूक्ष्म फरक व्यतिकरणमापक दर्शवू शकते.
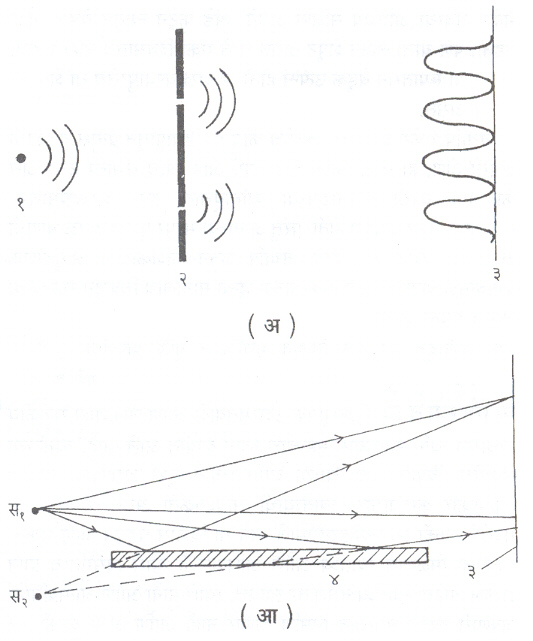
व्यतिकरणमापकांचे दोन वर्ग : व्यतिकरणमापकांत मुख्यत्वे दोन पद्धती वापरल्या जातात. ‘तरंगमुख विभाजन पद्धत’ व ‘परमप्रसर विभाजन पद्धत’ या त्या पद्धती होत. तरंगमुख विभाजन करण्याच्या दोन रचना आ. १मध्ये दाखविल्या आहेत. यंग द्विसूचिछिद्र व्यतिकरणमापकात [आ. १ (अ)] बिंदू-उद्‌गमातून निघाणारा प्रकाश दोन सूचिछिद्रांना प्रकाशित करतो [→ बंग, टॉमस]. सूचिछिद्रांनी विवर्तित केलेल्या प्रकाशामुळे दोन बिंदू-उद्‌गमांचे व्यतिकरण होते. लॉईड आरशाच्या प्रयोगात [आ. १ (आ)] स१ या बिंदू-उद्‌गमाची आरशामध्ये स२ ही प्रतिमा मिळते. स१ आणि स२ पासून निघणाऱ्या प्रकाश-शलाकांचे परस्परव्यापरी विभागामध्ये व्यतिकरण होते. तरंगमुखाचे विभाजन आणखीही काही रचनांद्वारे करता येते. या सर्व प्रकारांत उद्‌गमापासून निघालेल्या शलाकेचे दैशिक विभाजन होते व विवर्तन आरसे, लोलक अगर भिंगाच्या साहाय्याने विभाजित शलाकांचे एकमेकींवर अध्यारोपण करून व्यतिकरण आकृतिबंध मिळविला जातो.
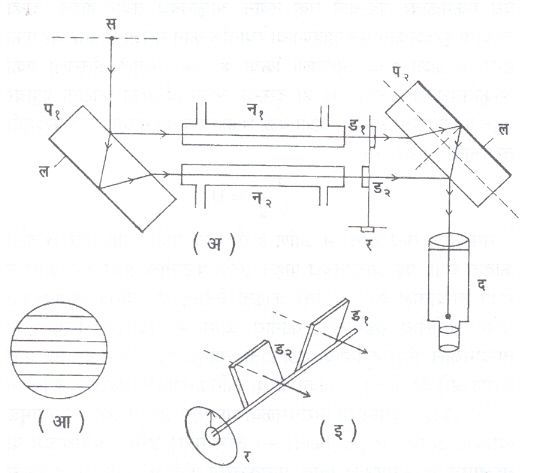
झामँ व्यतिकरणमापक : आ. २ मध्ये दाखविल्याप्रमाणे मागील बाजूस ॲल्युमिनियमाचा पातळ लेप (ल) दिलेल्या प१ आणि प२ काचेच्या जाड पट्ट्या आहेत. स ह्या एकवर्णी विस्तारित प्रकाश-उद्‌गमापासून निघालेले किरण प१ ह्या काचेच्या पट्टीवर पडतात आणि वेगवेगळ्या पृष्ठांपासून परावर्तित होऊन काही अंतरावरील प२ ह्या काचेच्या पट्टीवरून पुन्हा परावर्तित होऊन एकत्र आल्यावर व्यतिकरण पट्ट तयार होतात. यांना ‘बूस्टर पट्ट’ म्हणतात. द ह्या दूरदर्शकाद्वारे या व्यतिकरण पट्टांचे मापन करता येते. प१ व प२ या दोन पट्ट्यांदरम्यान न१ व न२ ह्या समान लांबीच्या नळ्या अशा प्रकारे ठेवल्या आहेत की, प१ मधून परावर्तित होणारे किरण न१ व न२ मधून जावेत. न२ नळीतील हवा काढून ती हळूहळू निऱ्यात करत गेल्यास हवेचा दाब कमी होताना दूरदर्शकामध्ये बघून किती पट्ट सरकले याचे मापन करता येते. हवेचा प्रणमनांक μ, तरंगलांबी ल, नळीची लांबी ट आणि विस्थापित पट्टांची संख्या Δ म असल्यास
(μ–१) ट = Δ म·ल
या समीकरणाद्वारे μ म्हणजेच हवेचा प्रणमनांक काढता येतो. याच उपकरणात ड१ व ड२ ह्या समान जाडीच्या काचेच्या छोट्या पट्ट्या न१ व न२ समोर अशा ठेवल्या की, ड१ही स्थिर राहील आणि ड२ ही स्क्रूच्या (र) साहाय्याने फिरवून तिच्यातून जाणाऱ्या प्रकाशकिरणाची लांबी बदलेल. न२ निर्वात करताना प्रकाशमार्गाची जी लांबी कमी होईल, त्याची भरपाईही ड२ पट्टी फिरवून करता येईल व त्यामुळे पट्ट हलणार नाहीत. ड२ ही काच किती फिरविली व हवेचा दाब किती कमी झाला यांवरून हवेचा प्रणमनांक काढता येतो.
मायकेलसन व्यतिकरणमापक : मायकेलसन व्यतिकरणमापकामुळेच सापेक्षता सिद्धांताची पार्श्वभूमी तयार झाली व वर्णपटरेषांची सूक्ष्म रचना अभ्यासण्यास सुरुवात झाली. मीटर या मानकाचे मूल्य प्रकाश-तरंगाच्या तरंगलांबीशी निगडित केले गेले. तसेच सूक्ष्म अंतराचे मापन करणाऱ्या शास्त्राचा पायाही घालण्यात आला.
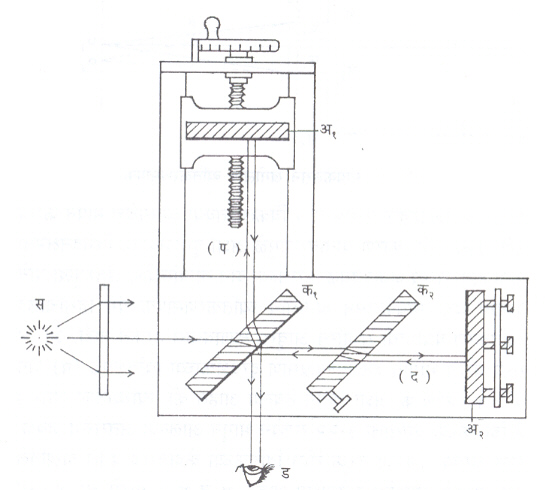
आ. ३ मध्ये दाखविल्याप्रमाणे स या प्रकाश-उद्‌गमापासून निघालेला किरण ४५० च्या कोनातील क१ या शलाका-विभागकावर पडतो. विभागकाच्या तळाला चांदीचा पातळ लेप (म) दिलेला असल्याने हा पहिला किरण (प) अर्धांशाने परावर्तित होतो आणि अर्धांशाने संक्रमित होऊन दुसरा किरण (द) हा क२ या काचपट्टीतून जाऊन अ२ ह्या आरशावरून परावर्तित होऊन येतो. परत क२ मधून जाऊन तो क१ वरून परावर्तित होतो. क१ पट्टीच्या तळापासून अर्धांशाने परावर्तित झालेला किरण अ१ ह्या आरशावरून परावर्तित होतो आणि क१ मधून संक्रमण पावून पहिल्या भागाबरोबर एकत्रित होतो. या दोन किरणांच्या व्यतिकरणामुळे पट्ट दिसतात. तेथे डने डोळा दर्शविला आहे. अ१ हा आरसा मळसूत्रावर बसविलेला असून तो मागे-पुढे करता येतो व त्याचे सूक्ष्म स्थानांतरही अचूक मोजता येते. जेव्हा अ१ आणि अ२ हे आरसे एकमेकांशी बरोबर काटकोन करतात तेव्हा व्यतिकरण पट्ट हे वर्तुळाकार असतात. जर अ१ व अ२ हे एकमेकांशी किंचित कलते असले, तर सरळ पट्ट मिळतात. प्रकाश-शलाकांचे मार्ग जेव्हा पूर्णतः समान लांबीचे असतात तेव्हा व्यतिकरण पट्ट पांढऱ्या प्रकाशातसुद्धा दिसू शकतात. मात्र एकवर्णी प्रकाशातील पट्टांपेक्षा त्यांची संख्या कमी (५ ते ६) असते. क२ ही काचपट्टी क१ ह्याच जाडीची असते. पहिल्या व दुसऱ्या (प व द) प्रकाशकिरणांचे मार्ग समान अंतराचे करण्यासाठी क२ चा वापर होतो, त्यामुळे त्या पट्टीस ‘पूरक पट्टी’ असे म्हणतात. अ१ हा आरसा किती पुढे-मागे सरकला आणि त्या काळात किती पट्ट सरकले यांवरून तरंगलांबी काढता येते. ज्यांच्या तरंगलांबीतील फरक अगदी थोडा आहे. [उदा., सोडियमच्या D वर्णपटरेषा ५८९६ Å आणि ५८९० Å मधील अंतर ६ Å आहे. (Å म्हणजे अँगस्ट्रॉम हे लांबीचे एकक असून १Å = १०-१० मी.)] असे तरंग एखाद्या प्रकाश-उद्‌गमात असतील, तर व्यतिकरणमापकात एकमेकांवर अध्यारोपित असे व्यतिकरण पट्ट दिसतील. अ१ हा आरसा पुढे-मागे केला, तर पट्टांची स्पष्टता कमी-अधिक होईल. ज्या वेळी एका तरंगामुळे निर्माण झालेले काळे पट्ट दुसऱ्या तरंगामुळे निर्माण झालेल्या तेजस्वी पट्टांवर पडतील, तेव्हा अस्पष्ट असे दृश्य दिसेल. नंतर अ१ आरसा पुढे सरकविल्यास पट्ट परत अधिक स्पष्ट दिसतील. अ१ आरसा परत पुढे नेल्यास ते आणखी अस्पष्ट होतील. पट्ट स्पष्ट दिसणाऱ्या किंवा अस्पष्ट दिसणाऱ्या वाचनांच्या फरकाद्वारे त्यांच्यातील तरंगलांबीचा फरक Δ ल काढता येतो.
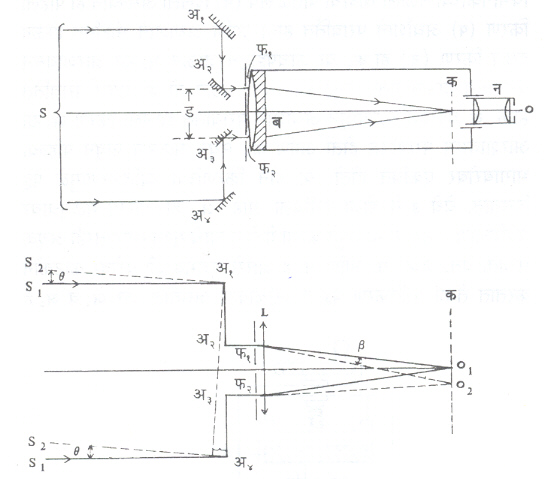
मायकेलसन खगोलीय व्यतिकरणमापक : या व्यतिकरणमापकाने ताऱ्यांचे ०·०१ विकलाइतके लहान व्यास मोजता येतात. पृथ्वीवरील मोठ्यातल्या मोठ्या दूरदर्शकाद्वारे ताऱ्याच्या १ विकलाइतक्या व्यासांचेच मापन करता येणे शक्य आहे. कारण वातावरणामुळे अशा दूरदर्शकांची विभेदनक्षमता कमी होते. तसेच जवळजवळ असलेल्या दोन ताऱ्यांमधील अंतरसुद्धा याने काढता येते. मायकेलसन खगोलीय व्यतिकरणमापक यंग द्विसूचिछिद्र व्यतिकरण प्रयोगाची सुधारित आवृत्ती म्हणावयास हरकत नाही. आ. ४मध्ये वरील भागात दाखविल्याप्रमाणे दूरदर्शकाच्या बिंबिकेपुढे (ब) दोन फटी फ१ आणि फ२ अशा रीतीने ठेवल्या आहेत की, त्यांच्यातील अंतर ड हे बिंबिकेच्या व्यासाला १.२२ संख्येने भागून आलेल्या अंतराच्या जवळपास असावे. (क या तुटक रेषेने बिंबिकेच्या केंद्रांतराचे प्रतल दाखविले आहे व न हे दूरदर्शकाचे नेत्रभिंग आहे.) अ१ ते अ४ हे आरसे आ. ४ मध्ये दाखविल्याप्रमाणे ठेवलेले असून अ१-अ२ तसेच अ३-अ४ या जोड्यांतील आरसे एकमेकांना समांतर आहेत. अ१ आणि अ४ यांमधील अंतर वाढविता येते. अ१ ला वर, तर अ४ला खाली सरकविता येऊ शकते, अशी रचना असलेला दूरदर्शक समजा दोन जवळजवळ असलेल्या ताऱ्यांकडे वळविला (आ. ४ मधील खालची आकृती),
|
|
तर दोन्ही ताऱ्यांचे व्यतिकरण आकृतिबंध एकमेकांवर पडल्याने एक नवीन आकृतिबंध तयार होईल. दोन्ही ताऱ्यांना दूरदर्शकापासून जोडणाऱ्या रेषांतील कोन समजा θ आहे, तर एका ठराविक अशा डच्या मूल्याला किंवा फ१–फ२मधील अंतराला एका आकृतिबंधाचा तेजस्वी पट्ट हा दुसऱ्या आकृतिबंधाच्या काळ्या पट्टावर पडून पट्ट दिसणार नाहीत. अशा वेळी ‘ल’ ही ताऱ्याकडून येणाऱ्या प्रकाशाची तरंगलांबी असेल, तर
ल
——— = θ
२ ड
हे समीकरण सत्य ठरते. ल आणि ड ची मूल्ये माहीत झाल्यावर θ कोन काढता येतो. पट्ट आकृतिबंध पाहून आणि फटीतील अंतर ड हे योग्य ते ठेवून ताऱ्यांतील कोनीय अंतरे काढता येतात. या व्यतिकरणमापकाचा वापर खगोलीय ग्रहगोलांचे कोनीय व्यास मोजण्यासाठी किंवा दोन ताऱ्यांमधील अंतर ठरविण्यासाठी होतो. त्यामुळे पट्ट सुस्पष्ट नसतात याचे कारण असे की, हे पट्ट ज्या किरणांच्या व्यतिकरणांद्वारे मिळतात ते किरण दूरच्या प्रकाश-उद्‌गमांच्या निरनिराळ्या भागांतून आलेले असतात. त्यामुळे त्यांच्यात अवस्थांतर [कलाकोन → तरंग गति] असते. अवस्थांच्या या बदलामुळे पट्ट अस्पष्ट दिसतात. मायकेलसन यांनी अ१ आणि अ४ हे आरसे वापरून, ते सम मितीत (सम प्रमाणात) सरकवून त्यांतील किरण-शलाकांतील अंतर य बदलले. असे करताना फटींतील अंतर बदलण्याची आवश्यकता नसते. चराचर विश्व पूर्णपणे व्यापून राहिलेल्या ईथर या काल्पनिक द्रव्याच्या संदर्भात मायकेलसन व एडवर्ड विल्यम्स मॉर्ली यांनी ‘मायकलेसन व्यतिकरणमापक’ वापरून केलेल्या प्रयोगाची माहिती मराठी विश्वकोशातील ‘ईथर-२’ या नोंदीत आली आहे.
|
|
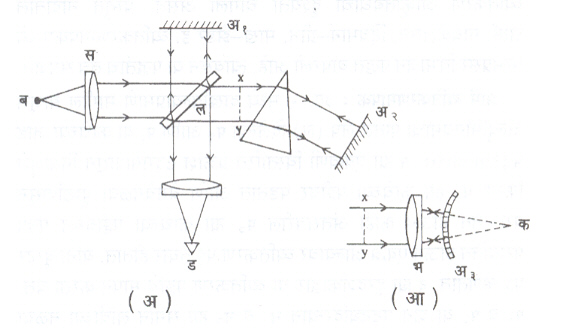
टि्वमान-ग्रीन व्यतिकरणमापक : मायकेलसन व्यतिकरणमापकात बिंदू-उद्गम वापरला, तर तो टि्वमान-ग्रीन व्यतिकरणमापकाचे कार्य करतो. अंतर्गोल व बहिर्गोल आरसे, भिंगे, सपाट आरसे इ. प्रकाशकीत लागणाऱ्या घटकांच्या वक्रता किंवा सपाटपणा तपासण्यासाठी या व्यतिकरणमापकाचा उपयोग होतो. आ. ५ मध्ये दाखविल्याप्रमाणे बिंदू-उद्‌गमापासून (ब) मिळणारी किरणे समांतरित्रातून (स) जाऊन ४५० कोन केलेल्या व ॲल्युमिनियमाचा लेप (ल) दिलेल्या शलाका विभागकावर पडतात. अर्धांशाने ती अ१ व अ२ ह्या पृष्ठांकडे जाऊन परावर्तित होऊन येतात आणि व्यतिकरणाचा आकृतिबंध देतात. अ१ हा साधा आरसा असून त्याला संदर्भपृष्ठ म्हणतात, तर अ२ह्या ठिकाणी ज्याची चाचणी घ्यावयाची आहे असे भिंग, दुसरा सपाट आरसा इ. ठेवलेले असतात. अ२ आरसा हा अगदी सपाट असल्यास व्यतिकरण पट्ट समान अंतरावर असून सरळ असतात. ज्या ठिकाणी पट्ट वाकडे होतात किंवा त्यांच्यातील अंतर बदलते त्या भागास आरसा सपाट नाही, असे सिद्ध होते (आ. ६). अ१ आरशास कलते करून पट्टांवर काय परिणाम होतो, हे डोळ्याने (ड) बघता येते व त्यायोगे चाचणी-आरशाच्या प्रतलातील उंचसखलपणाचा अंदाज येतो. टि्वमान-ग्रीन व्यतिकरणमापकात लेसर-प्रकाश-उद्‌गमाचा वापर केल्यास दोन्ही बाजूंना असणाऱ्या आरशांची अंतरे थोडी अधिक कमी असूनसुद्धा व्यतिकरण पट्ट उठावदार आणि स्पष्टपणे दिसतात. लेसर उद्‌गमाच्या वापराने या व्यतिकरणमापकाची उपयुक्तता अनेक पटींनी वाढून ते बहुमोल साधन बनते. भिंग-चाचणीच्या रचनेच्या आ. ५ (आ) मध्ये भिंग (भ), बहिर्वक्र आरसा (अ३) व त्याचे केंद्र (क) दाखविले आहेत.
|
|
फीझो व्यतिकरणमापक : प्रकाशकीय मापनशास्त्रात या व्यतिकरणमापकाचा अधिक वापर होतो. हे एक प्रकारचे टि्वमान-ग्रीन व्यतिकरणमापकच आहे. फरक एवढाच की, अ१ आणि अ२ या पृष्ठभागांना एकमेकांशी काटकोनात न ठेवता अ२ हे भिंग किंवा अंतर्गोल आरसा इ. चाचणी घटक अ१ ह्या सपाट अशा संदर्भ-आरशाला बिलगून ठेवला जातो. चाचणी घटकाच्या पृष्ठापासून आलेले परावर्तित किरण आणि संदर्भपृष्ठापासून परावर्तित होऊन आलेले किरण यांच्यातील व्यतिकरणामुळेच पट्टांचा आकृतिबंध तयार होतो. अ१आरशावर ठेवलेला चाचणी आरसा किंवा काचेचा तुकडा हा अगदी सपाट असेल, तर पट्ट सरळ आणि समान अंतरावर असतात. जर पट्ट वाकडे असतील, तर पृष्ठभाग उंचसखल असतो. एक पट्टाचा फरक एखाद्या ठिकाणी दिसत असल्यास स्पर्श करीत असलेल्या पृष्ठांमधील अंतर त्या प्रकाश-उद्गम-तरंगाच्या तरंगलांबीच्या निम्मे असते. उदा., हीलियम लेसर वापरत असल्यास (तरंगलांबी ५७८·५५ नॅनोमीटर) एका पट्टाचा फरक अदमासे ०·३ मायक्रोमीटर (μm : १ मायक्रोमीटर = एक दशलक्षांश मीटर) एवढे अंतर दाखविते.
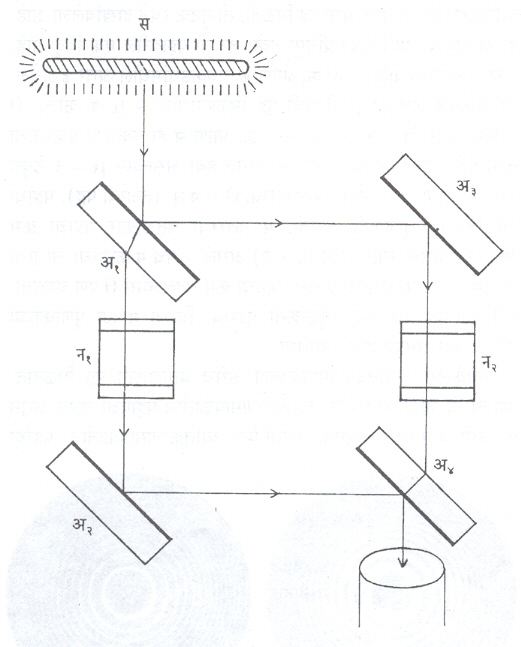माख-झेंडर व्यतिकरणमापक : आ. ७ मध्ये दाखविल्याप्रमाणे या व्यतिकरणमापकामध्ये अ१ आणि अ४ या समान जाडीच्या काचेच्या पट्टिका असून एका बाजूस त्यांवर चांदीचा पातळ लेप दिलेला असतो. अ२ आणि अ३ हे आरसे आहेत. अ१, अ२, अ३ व अ४ हे एकमेकांना समांतर तर आहेतच, पण अ१ – अ२ हे अंतर अ२ – अ४ इतके आहे. तसेच अ१ – अ२ आणि अ३ – अ४ ही अंतरेपण समान आहेत. न१ आणि न२ ह्या समान लांबीच्या नळ्या अ१ – अ२ आणि अ२ – अ४ ह्या मार्गात ठेवलेल्या आहेत. अ१ आरशावर आलेल्या प्रकाश-शलाकांचे अर्धांशाने संक्रमण होते व अर्धांशाने परावर्तन होते. परावर्तित किरण अ३ आरशापासून परत परावर्तित होतात आणि अ४ मधून संक्रमित होतात. अ१ मधून संक्रमित झालेले किरण अ२ वरून परावर्तित होऊन परत अ४ येथूनही परावर्तित होतात. अशा रीतीने अ३ कडून आणि अ२ कडून आलेल्या किरणांचे व्यतिकरण होऊन पट्ट मिळतात. विमानाभोवती हवेचा दाब कसा कसा बदलतो हे पाहण्यासाठी हे उपकरण प्रथम वापरण्यात आले. न१ व न२ ह्यांपैकी एका नळीतील हवेचा दाब जर जास्त झाला, तर त्या हवेचा प्रणमनांक वाढतो. परिणामतः प्रकाश-पथ अधिक लांबीचा होतो आणि पट्टाचे विस्थापन होते (हा प्रकार झामँ व्यतिकरणमापकामध्येही घडतो). विमाने, रॉकेटे (अग्निबाण) व प्रक्षेपणास्त्रे यांच्या भोवताली हवेचा दाब कसा कसा बदलतो, हे पाहण्यासाठी या व्यतिकरणमापकाचा उपयोग होतो. मायकेलसन व्यतिकरणमापकामध्ये अशी परमप्रसराची विभागणी होऊन पट्टांचा जसा आकृतिबंध मिळतो तसेच येथेही होते पण मायकेलसन व्यतिकरणमापकात क१ आणि क२ (आ. ३) ह्या काचेच्या पट्ट्यांतून किरण अनुक्रमे तीन व दोन वेळा जातात. तसे माख-झेंडर व्यतिकरणमापकात होत नाही. अ१ पासून अ४ येथे येईपर्यंत संक्रमित किरण आणि परावर्तित किरण आपापला मार्ग फक्त एकदाच क्रमित करतात. मायकेलसन व्यतिकरणमापकामध्ये समजा प्रकाश-शलाका एका दिशेने जात आहे, जाताना आणि आरशावरून परावर्तित होऊन येताना स्थानिक कारणांमुळे हवेचे प्रणमनांक जर बदलले, तर पट्ट अस्पष्ट होऊ शकतात. प्रसंगी दिसूही शकणार नाहीत. माख-झेंडर व्यतिकरणमापकात तसे घडत नाही, हा एक फायदा आहे.
फाब्री-पेरॉ व्यतिकरणमापक : आतापर्यंत वर्णन केलेल्या व्यतिकरणमापकांमध्ये दोन प्रकाश-शलाकांद्वारे व्यतिकरण घडून येते. आ. ८ मध्ये दाखविल्याप्रमाणे क१ आणि क२ या साधारणतः ६ सेंमी. व्यासाच्या व ३ ते ४ मिमी. समान जाडीच्या काचेच्या तबकड्या घेऊन, त्यांच्या एकेका बाजूला चांदीचा पातळ लेप देऊन त्या बाजू अधिक परावर्तनक्षम केलेल्या असतात. या बाजू एकमेकींसमोर येतील, पण अलग राहतील अशा रीतीने त्यांच्यामध्ये विभागक ठेवून त्यांना चौकटीत बसविलेले असते. त्या एकमेकींना पूर्णतः समांतर करता याव्यात ह्यासाठी चौकटीवर दाब स्क्रूची योजना केलेली असते. या तबकड्यांमधील अंतर १ मीमी.पासून ते सेंमी.पर्यंत असू शकते.
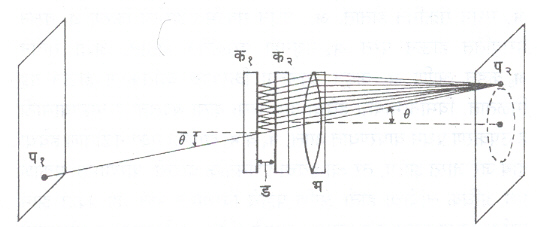एका विस्तररित (चौकोनी) प्रकाश-उद्‌गमापासून म्हणजे प१ ह्या बिंदूतून निघालेल्या किरणाचे क१ आणि क२ ह्या तबकड्यांमध्ये वारंवार परावर्तन होते. दर वेळी संक्रमणामुळे बाहेर पडणाऱ्या किरणांची एक शलाका तयार होऊन बहिर्गोल भिंगांच्या (भ) साहाय्याने ती प२ ह्या ठिकाणी केंद्रित केली जाते. हे सर्व किरण एकाच प्रकाशबिंदूपासून निघालेले असल्याने त्याचे व्यतिकरण होऊन गोल असा पट्ट मिळतो. तो तुटक रेषेने दाखविलेला आहे. प२ हा बिंदू प१ ह्या बिंदूची प्रतिमा नव्हे, तर तो पट्टावरील एक बिंदू आहे, हे ध्यानात घेतले पाहिजे. जर क१ आणि क२ तबकड्यांमधील अंतर इ असेल, तर संक्रमण-शलांकाद्वारे तेजस्वी पट्ट मिळण्यासाठी २ μ..ड कोज्या = θ म.ल. (येथे म = १, २, ३ ……. इ. आणि ल ही एकवर्णी प्रकाशाची तरंगलांबी आहे.) तबकड्यांमधील जागेत हवा असल्यास μ= १ ठेवून हेच समीकरण असे होते : २ ड कोज्या θ = म.ल (तेजस्वी पट्ट). पट्टांचा आकृतिबंध वर्तुळाकृती असतो. म नंतरच्या वर्तुळाकार पट्टाचा क्रम (म + १) असेल, त्यानंतरचा (म + २) असेल. तसेच म क्रमाच्या आधीचा पट्ट (म – १) ह्या क्रमाचा असेल. पट्टाचा क्रम बदलल्यास θ पण बदलतो, हेही ध्यानात येते. या वर्तुळाकृती पट्टांच्या त्रिज्या म ह्या पूर्णाकांच्या वर्गमूळाच्या सम प्रमाणात असतात.
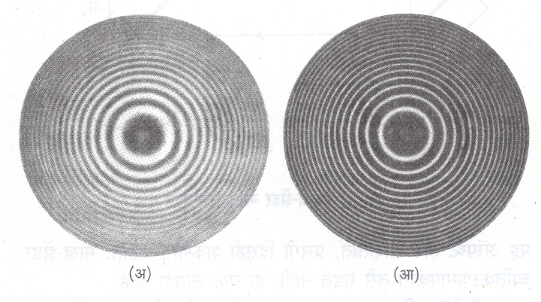मायकेलसन व्यतिकरणमापकातही असेच वर्तुळाकृती पट्ट मिळतात पण त्यांची जोडी फाब्री-पेरॉ व्यतिकरणमापकातील पट्टांपेक्षा जास्त असून ते कमी धारदार असतात. फाब्री-पेरॉ व्यतिकरणमापकातील पट्टांचा आकृतिबंध सुस्पष्ट रेखीव आणि उठावदार असतो (आ. ९). फाब्री-पेरॉ व्यतिकरणमापकाचा विशेष उल्लेखनीय गुणधर्म म्हणजे त्याची ‘सूक्ष्मता’ हा होय. लागोपाठच्या कोणत्याही दोन तेजस्वी पट्टांमधील अंतर भागिले पट्टाची अर्धजाडी म्हणजे व्यतिकरणमापकाची सूक्ष्मता होय. फाब्री-पेरॉ व्यतिकरणमापकातील सूक्ष्मता फ खालील सूत्राद्वारे देतात.
Π √र
फ = ———–
(१ – र)
येथे र हा चांदीचा लेप दिलेल्या काचेचा परावर्तनांक आहे. फाब्री-पेरॉ व्यतिकरणमापकाची विभेदनक्षमता (व) खालील सूत्राद्वारे देतात.
λ फ. २ .μ ड
व = ———- = —————-
(Δ λ)min ल
५००० Å तरंगलांबी असलेल्या हिरव्या रंगाच्या प्रकाशकिरणासाठी तबकड्यांतील अंतर १० मिमी. असेल तर आणि त्यांचा परावर्तनांक ९०% असेल, तर फाब्री-पेरॉ व्यतिकरणमापकाची विभेदनक्षमता १०६ इतकी येते.
एकवर्णी वाटणाऱ्या प्रकाशात जर जवळजवळ तरंगलांबी असलेले तरंग असतील, तर फाब्री-पेरॉ व्यतिकरणमापकाद्वारे मिळालेल्या व्यतिकरण पट्टाच्या आकृतिबंधातसुद्धा त्या तरंगांचे वेगवेगळे पट्ट असलेला संमिश्र आकृतिबंध दिसू शकतो. [→ फाब्री, (मारी पॉल ऑग्यूस्त) शार्ल].
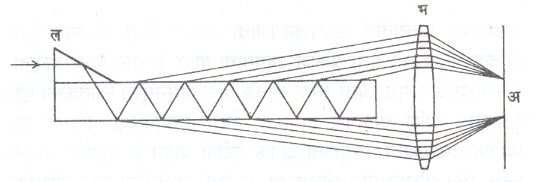लुमर-गेहरके पट्टिका : आ. १०मध्ये दाखविल्याप्रमाणे एका कॉर्ट्स या खनिजाच्या लांब अशा पट्टिकेवर एका टोकाला एक काटकोन त्रिकोणाकृती लोलक (ल) बसविलेला आहे. ह्या लोलकाच्या कर्णाकडील पृष्ठभागावर चांदीचा लेप दिल्याने तो पूर्णपणे परावर्ती आहे. प्रकाशकिरण या लोलकाच्या पृष्ठावर पडून परावर्तित होऊन त्या पट्टिकेत सीमान्त कोनात प्रवेश करतो आणि पट्टिकेच्या वरच्या आणि खालच्या पृष्ठांपासून त्याचे वारंवार परावर्तन घडते. दोन्ही बाजूंनी काही अंशी संक्रमित झालेले किरण बहिर्गोल भिंगाने (भ) केंद्रित करून व्यतिकरणाचा आकृतिबंध (अ) मिळविता येतो. अलीकडे लुमर-गेहरके पट्टिका वापरण्याऐवजी फाब्री-पेरॉ व्यतिकरणमापक वापरण्याकडे अधिक कल आहे, तरीपण लुमर-गेहरके पट्टिका या साध्या उपकरणानेही उच्च विभेदनक्षमता मिळू शकते.
होलोग्राफिक व्यतिकरणमापक : जेव्हा एखाद्या तरंगाचे स्वलेखामध्ये म्हणजे होलोग्रॅममध्ये [कॅमेरा न वापरता छायाचित्रीय फिल्मवर किंवा पट्टिकेवर तयार होणाऱ्या वैशिष्ट्यपूर्ण त्रिमितीय चित्रामध्ये → होलोग्राफी] आलेखन केले जाते तेव्हा त्याची नंतर पुनर्रचना करून उपयोग करता येतो. होलोग्राफिक (स्वलेखनकारी) व्यतिकरणमापनामध्ये याच तत्त्वाचा उपयोग केला जातो. प्रथम एखाद्या तरंगाचे होलोग्राफिक आलेखन करून ठेवण्यात येते आणि नंतर त्याची पुनर्रचना करून ज्या तरंगाशी तुलना करावयाची आहे त्याच्याशी या आलेखित तरंगाचे व्यतिकरण करण्यात येते. या होलोग्रॅमच्या रूपात आधीच साठवून ठेवण्याच्या (किंवा काल-विलंब) तंत्रामुळे परंपरागत अशा व्यतिकरणमापन पद्धतीपेक्षा होलोग्राफिक व्यतिकरणमापन अधिक फायदेशीर सिद्ध झाले आहे. कुठल्याही आकाराच्या आणि कोणत्याही पृष्ठांचा प्रथम होलोग्रॅम तयार केला जातो. या होलोग्रॅमला तो आलेखन केला जाताना जे तरंगमुख वापरले गेले असते त्याने प्रकाशित केल्यास मूळ वस्तूचे तरंगमुख तयार होते. हा होलोग्रॅम त्याच्या मूळ जागी धरल्यास व निरीक्षकाने त्यातून बघितल्यास मूळ वस्तू आणि तिची होलोग्राफिक प्रतिमा या दोन्ही गोष्टी दिसतील. मूळ वस्तूमध्ये थोडे जरी विरूपण आले किंवा निर्माण केले गेले, तर व्यतिकरण पट्टांचा आकृतिबंध तयार होऊन किती विरूपण आले, ते कळू शकते. मूळ वस्तूच्या आकारापासून तिच्या आकारात किती बदल झाला हे या तंत्राने कळते. द्विप्रकाशन पद्धतीत विरूपणापूर्वी एका होलोग्रॅमचे व विरूपणानंतर दुसऱ्या होलोग्रॅमचे अंकन करतात. या दोन्ही होलोग्रॅमच्या पुनर्निर्मित निरीक्षणातून त्यांच्यात किती विरूपण झाले ते कळते. या पद्धतीतील उणीव म्हणजे एखाद्या पृष्ठभागात विरूपण सतत होत असल्यास त्याचा अभ्यास करता येत नाही. फक्त विरूपणामधील फरक काढता येतो. वेळेची सरासरी काढणाऱ्या तंत्रामध्ये एखाद्या कंपन पावणाऱ्या कालीघात सरासरी (मध्यममान) काढलेल्या पृष्ठाचा काल-सरासरी होलोग्रॅम आलेखित करता येतो. कंपन पावणाऱ्या पृष्ठाचा परमप्रसर समजा ८ ते १० तरंगलांबीएवढा असेल, तर प्रकाशित केलेल्या होलोग्रॅममध्ये एकमेकांवर अध्यारोपित अशा व्यतिकरण पट्टांचा आकृतिबंध मिळतो. हे पट्ट म्हणजे पृष्ठांचे समान विस्थापन झालेल्या आकररेषा होत. [→ होलोग्राफी].
स्पेकल व्यतिकरणमापन : लेसरसारख्या सुसंगत (कलामेलित) उद्‌गमाचा किरण एखाद्या खडबडीत पृष्ठभागावर (किंवा असमांग माध्यमावर) पडल्यानंतर तेजस्वितेचे जे स्वैर वितरण होते, त्या आकृतिबंधास स्पेकल असे म्हणतात. यामुळे तो पृष्ठभाग (किंवा माध्यम) कणीदार किंवा रवाळ भासतो. वस्तूंची कंपने, विस्थापने आणि विरूपण यांच्या मापनासाठी या तंत्राचा वापर होतो. स्पेकल व्यतिकरणमापनाचा या कामी वापर वाढवण्याचे प्रमुख कारण म्हणजे हे मापन करताना यांत्रिकी घटक अनाशिवंत राहतात. काल-सरासरी छायाचित्रणामध्ये वस्तूंच्या एकाच प्रतलातील कंपनांचे पृथःकरण करता येते. खगोलीय स्पेकल व्यतिकरणमापन ही एक नवीन शाखा उदयास येत आहे. पृथ्वीवरील उपकरणांद्वारे खस्थ पदार्थांचा अभ्यास करताना वातावरणातील क्षुब्ध प्रवाहांचा त्यांच्या विभेदनक्षमतेवर प्रभाव पाडून ती घटते, पण स्पेकल व्यतिकरणमापनाने ही अडचण दूर केली आहे. या तंत्रामध्ये एखाद्या ग्रहाची किंवा ताऱ्याची शेकडो चित्रे थोड्या थोड्या कालावधींनी घेतात. अशी चित्रे आलेखित करताना देण्यात येणारा प्रकाशन वेळ हा अगदी अल्प असा असतो. नंतर या सर्व छायांकनांचे फूर्ये रूपांतर [→ फूर्ये श्रेढी] करून त्यांचे एकत्रीकरण करून त्यांचा वर्ग केल्यास विवर्तन आकृतिबंध मिळतो. परत फूर्ये रूपांतर करून दैशिक स्वयं परस्परसंबंध-फलनाद्वारे [→ फलन] ग्रहगोलांचे मापन करतात.
पहा : तरंग गति ध्वनिकी प्रकाशकी प्रणमनांकमापन मापनविज्ञान वर्णपटविज्ञान वातविवर विभेदनक्षमता विवर अनुस्पंदक.
संदर्भ : 1. Hariharan, P. Basics of Interferometry, 1991.
2. Rastogi, P. K. Holographic Interferometry : Principles and Methods, 1994.
3. Steel, V. H. Interferometry, 1985.
बेहरे, सुभाष ह.
“