विवृत्त : हा एक बंदिस्त वक्र आहे. मेनीक्मस (इ. स. पू. सु. ३५०) व ⇨पेर्गाचे ॲपोलोनियस (इ. स. पू. २६१-२००) या ग्रीक गणितज्ञांना विवृत्त या वक्राची माहिती होती व त्यांनी विवृत्ताचे अनेक गुणधर्म शोधले होते. तसेच भारतीय गणितज्ञ ⇨महावीर (इ. स. नववे शतक) यांनी विवृत्ताचे विवरण करून विवृत्ताचे क्षेत्रफळ व परिमिती यासंबंधीची सूत्रे दिली होती.
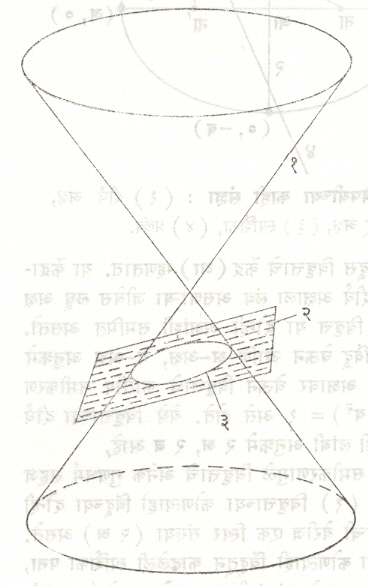
एखादे प्रतल जर जात्य वृत्तशंकूच्या शिरोबिंदूच्या एकाच बाजूस असलेल्या वक्रपृष्ठाचा छेद घेत असेल आणि ते शिरोबिंदूतून जात नसेल तर त्याद्वारे मिळणारा छेद विवृत्त असतो. (आ. १). म्हणून हा वक्र शंकुच्छेद किंवा शांकव कुलातील एक वक्र आहे. साहजिकच शंकुच्छेदाचे सर्व गुणधर्म विवृत्ताला लागू पडतात [⟶ शंकुच्छेद]. तथापि या संश्लेषक भूमितीच्या पद्धतीपेक्षा वैश्लेषिक भूमितीच्या साहाय्याने [⟶ भूमिति] विवृत्ताचा अभ्यास अधिक सोपा होत असल्याने त्या अभ्यासाची सुरुवात खालील व्याख्येने करतात. एखाद्या बिंदूचे दिलेल्या विशिष्ट स्थिर बिंदूपासूनचे (नाभीपासूनचे) अंतर व दिलेल्या विशिष्ट स्थिर रेषेपासूनचे (नियत रेषेपासूनचे) अंतर यांचे गुणोत्तर जर एक स्थिर संख्या ‘इ’ (विकेंद्रिता) असेल आणि इ < १ असेल, तर त्या बिंदूचा बिंदुपथ म्हणजे विवृत्त होय. (आ. २). या व्याख्येवरून काढलेल्या विवृत्ताचे कार्तीय समीकरण हे क्ष, य या कार्तीय निर्देशक चलांमधील द्विघातीय समीकरण असते [⟶ भूमिति शंकुच्छेद].
वरील समीकरण छोटे, सुटसुटीत होण्यासाठी खालील माहितीचा उपयोग होतो. विवृत्ताची एक नाभी ना, एक नियत रेषा व विकेंद्रिता माहीत असेल, तर त्यावरून त्याची दुसरी नाभी ना’ व दुसरी नियत रेषा काढता येते. या दोन नाभींतून जाणाऱ्या विवृत्ताच्या जीवेस त्याचा दीर्घ अक्ष म्हणतात (आ.३). दोन नाभींच्या मध्यबिंदूस विवृत्ताचे केंद्र (आ) म्हणतात. या केंद्रातून जाणाऱ्या दीर्घ अक्षाला लंब असणाऱ्या जीवेस लघू अक्ष म्हणतात (आ.३). विवृत्त या दोन्ही अक्षांशी सममित असतो. विवृत्त केंद्र हा आदिबिंदू घेऊन आणि क्ष-अक्ष, य-अक्ष अनुक्रमे दीर्घ अक्षावर व लघू अक्षावर घेऊन विवृत्ताचे कार्तीय समीकरण (क्ष२/अ२) + (य२/ब२) = १ असे होते. येथे विवृत्ताच्या दीर्घ अक्ष व लघू अक्ष यांची लांबी अनुक्रमे २ अ, २ ब आहे.
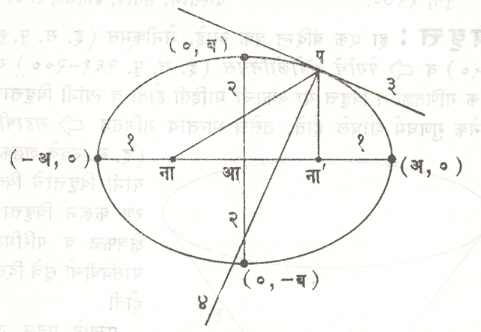
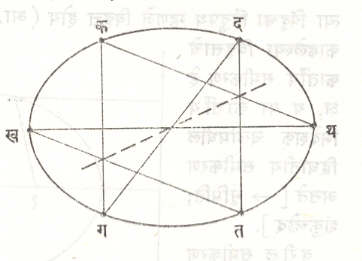
गुणधर्म : वरील समीकरणामुळे विवृत्ताचे अनेक गुणधर्म सहज सिद्ध करता येतात : (१) विवृत्ताच्या कोणत्याही बिंदूच्या दोन्ही नाभींपासूनच्या अंतराची बेरीज एक स्थिर संख्या (२ अ) असते. (२) विवृत्ताच्या प या कोणत्याही बिंदूतून काढलेली स्पर्शिका पना, पना’ या नाभींना जोडणाऱ्या रेषाखंडांशी समान कोन करते (आ. ३). (३) विवृत्ताच्या समांतर जीवांच्या मध्यबिंदूचा बिंदुपथ त्याच्या केंद्रातून जाणारी एक जीवा असते. तिला विवृत्ताचा व्यास म्हणतात. (४) या समांतर जीवांपैकी एक व्यासच असते. अशा प्रकारे मिळणाऱ्या विवृत्ताच्या दोन व्यासांना संयुग्मी व्यास म्हणतात. (५) कोणतीही रेषा विवृत्तास दोन बिंदूत, तर दुसरा कोणताही विवृत्त दिलेल्या विवृत्तास चार बिंदूंत, तर दुसरा कोणताही विवृत्त दिलेल्या विवृत्तास चार बिंदूत छेदतो. (६) पास्काल प्रमेय : विवृत्तामध्ये अंतर्लिखित केलेला कखगतथद हा कोणताही षट्‌कोन असेल, तर (कग, खत), (खथ, गद), (तद, थक) या जीवांच्या जोड्यांचे छेदनबिंदू एकरेषीय असतात (आ.४). द्वित्व तत्त्वाने विवृत्ताला परिलिखित(सीमाबद्ध) षट्‌कोनाचे विरुद्ध बिंदू जोडणाऱ्या रेषा काढल्यास छेदनबिंदू एकरेषीय असतात. याला ब्रीआंशाँ प्रमेय म्हणतात.
विवृत्त हा एक बंदिस्त वक्र असून त्याने सीमित केलेले लघुक्षेत्र हा एक बहिर्वक्र संच आहे. म्हणजे दोन बिंदू या संचात असल्यास त्यांना जोडणारा पूर्ण रेषाखंड या संचात असतो. या लघुक्षेत्रात किंवा विवृत्तावर नसणारे प्रतलाचे बिंदू विवृत्ताच्या बाहेर असतात. हाही एक बहिर्वक्र संच आहे. अशा प्रकारे विवृत्तामुळे प्रतलावरील सर्व बिंदूंचे तीन वियुक्त संचांत विभाजन होते. विवृत्ताच्या दोन अक्षांची लांबी २ आ. २ ब असेल, तर त्याच्या अंतर्भागाच्या लघुक्षेत्राचे क्षेत्रफळ π अब असते. अ = ब असेल तर त्या विवृत्ताला वर्तुळ म्हणतात. मात्र वर्तुळकंसाची लांबी काढण्याच्या सुव्यक्त सूत्रासारखे विवृत्त कंसाची लांबी काढण्याचे सूत्र उपलब्ध नाही. असे सूत्र काढण्याच्या प्रयत्नातून विवृत्तीय फलन, विवृत्तीय समाकल या गणित शाखांचा उगम झाला.
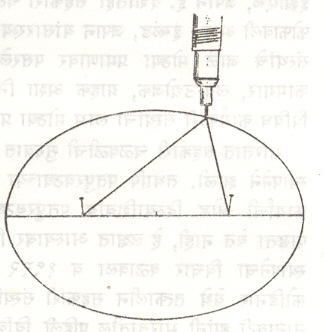अनुरेखन व उपयोग : वरील गुणधर्मांपैकी गुणधर्म (१) चा उपयोग करून विवृत्त कागदावर काढता येतो. दोन निरनिराळ्या ठिकाणी कागदावर एक एक टाचणी टोचून त्यांना एका दोऱ्याचे एक एक टोक बांधा. दोऱ्याची लांबी टाचण्यांमधील अंतरापेक्षा जास्त असावी. आता एक पेन्सिल दोऱ्यात घालून तिचे टोक कागदावर अशा रीतीने फिरवा की पूर्ण दोरा नेहमी ताठ राहील(आ.५). पेन्सिल विवृत्त रेखाटील.२अ, २ब अशी अक्षांची लांबी असलेले विवृत्त काढायचे असेल, तर अ+ब लांबीची एक सरळ पट्टी (काठी) घेऊन तिला एका टोकापासून अ एवढ्या अंतरावर पेन्सिल घट्ट बसवा. आता पट्टीची दोन टोके परस्परांना लंब असणाऱ्या एका कागदावरील दोन स्थिर रेषांवर नेहमी राहतील अशा रीतीने पट्टी फिरवा. हव्या असलेल्या विवृत्ताचे अनुरेखन पेन्सिलीने होईल. गुणधर्म (२) वरून ना या नाभीपासून निघालेला कोणताही ध्वनी वा प्रकाश तरंग विवृत्तावर परावर्तित होऊन ना’ या नाभीतून जाईल. याच गुणधर्माचा उपयोग विवृत्ताकार कुजबुजणाऱ्या सज्जांत होतो. शास्त्रज्ञांचे विवृत्ताकडे विशेष लक्ष जाण्याचे कारण हे की, न्यूटन यांच्या ⇨गुरुत्वाकर्षणाच्या व्यस्त वर्ग नियमाप्रमाणे प्रत्येक ग्रह सूर्याकडे आकर्षित होतो व त्यामुळे त्याचा सूर्याभोवतीचा मार्ग हा नाभिस्थानी सूर्य असलेला विवृत्त होतो. याच नियमाने अथांग विश्वातील अनेक छोटे स्वस्थ पदार्थही मोठ्या स्वस्थ पदार्थांभोवती विवृत्ताकार फिरतात.
पहा : भूमिति वक्र शंकुच्छेद.
संदर्भ : 1. Johnson, D. A. Curves in Space, New York, 1968.
2. Riddle, D. F. Analytic Geometry, New York, 1992.
3. Samuel, P. Projective Geometry, New York, 1988.
4. Yates, R. C. Handbook of Curves and their Properties, Baltimore, 1959.
कस्तुरे, दा. य.
“