विभेदनक्षमता : अत्यंत समीप असलेल्या व नुसत्या डोळ्यांनी पाहिल्या असता भिन्न न दिसता एकमेकांत मिसळून गेल्यासारख्या भासणाऱ्या वस्तूंच्या, एखाद्या प्रकाशीय उपकरणांद्वारे (उदा., भिंगव्यूह) मिळणाऱ्या प्रतिमांचे, भिन्नत्वाने स्पष्टपणे दिसणे या गोष्टीस त्या वस्तूंचे ‘विभेदन’ अशी संज्ञा आहे आणि असे विभेदन करण्याच्या त्या उपकरणाच्या क्षमतेच्या संख्यात्मक मापनास ‘विभेदनक्षमता’ म्हणतात. साधारणतः विभेदनक्षमता ही संज्ञा दोन अर्थांनी वापरली जाते. (१) दूरदर्शकाच्या मदतीने समीप असलेल्या दोन वस्तू (किंवा एकाच वस्तूवरील दोन भिन्न बिंदू) तपासणे किंवा सूक्ष्मदर्शकाच्या साहाय्याने एखाद्या वस्तूची सूक्ष्म संरचना अभ्यासणे व (२) ⇨विवर्तन जालकासारख्या उपकरणाच्या मदतीने शेजारीशेजारी असलेल्या दोन वर्णपट रेषांचे (दोन भिन्न तरंगलाव्यांचे) विभेदन करणे. विभेदनक्षम प्रतिमा असलेल्या वस्तूवरील सर्वात जवळच्या दोन बिंदूंमधील कोणीय किंवा रैखिक अंतरावरून दूरदर्शक, सूक्ष्मदर्शक इ. प्रकारच्या उपकरणांची विभेदन सीमा ठरवितात. तसेच भिनन वर्णातील विभेदनक्षम वर्णपट रेषांच्या तरंगलांब्यांतील सर्वात कमी फरकावरून वण्रपटविज्ञानीय उपकरणांची विभेदन सीमा ठरवितात. या राशी जितक्या लहान तितकी विभेदनक्षमता जास्त. सैद्धांतिक अगर प्रायोगिक अशा दोन्ही पद्धतींनी विभेदनक्षमता ठरविता येते. सैद्धांतिक पद्धतीत, प्रकाशीय उपकरणाच्या सर्व घटकांचे कार्य आदर्शवत आहे असे मानून, तरंग व विवर्तन सिद्धांत [⟶प्रकाशकी] वापरून विभेदनक्षमता ठरविली जाते. भिंगांतील विकृती व विवर्तन जालकाच्या रेषांमधील दोषांमुळे प्रायोगिक विभेदनक्षमता सैद्धांतिक मूल्यांपेक्षा सामान्यतः कमी असते. त्यामुळे सैद्धांतिक मूल्य विभेदनाची कमाल मर्यादा दाखविते.
लोलक, जालक, व्यतिकरणमापक [⟶ व्यतिकरणमापन] इ. वर्णपटविज्ञानीय उपकरणांसाठी वर्णयुक्त विभेदनक्षमता ही संज्ञा वापरली जाते व समी.(१) वापरून ती ठरविता येते.
R =λ /δλ … … … … … (१)
येथे λविभेदित वर्णपट रेषांच्या तरंगलाब्यांचे सरासरी मूल्य असून δλहा त्यांमधील फरक आहे.
अलीकडे विभेदनक्षमता ही संज्ञा केवळ प्रकाशीय व्यूहरचनेपुरतीच मर्यादित राहिली नसून ती ऊर्जा वर्णपट (कोणत्याही प्रकारच्या प्रारणाची- तरंगरूपी ऊर्जेची –तीव्रता त्याच्या ऊर्जेचे फलन म्हणून केलेले आलेखन, छायाचित्रीय नोंद वा अन्य दृकदर्शन), ⇨छायाचित्रण,द्रव्यमान, वर्णपटलेखक [⟶ द्रव्यमान वर्णपटविज्ञान], ⇨रडार, ⇨रेडिओ दूरदर्शकइत्यादींस अनुलक्षनही वापरतात.
प्रकाशकीमध्ये विभेदन याचा अर्थ भिंगासारख्या विवर्धकाच्या साहाय्याने दोन अत्यंत जवळच्या वस्तूंमधील अंतरांचे वर्धन करणे किंवा वर्णपटमापकाच्या मदतीने दोन अतिसमीप तरंगांब्यांमधील अंतर दृश्यमान करणे असा होतो. वेगवेगळ्या उपकरणांच्या विभेदनक्षमतेची माहिती खाली दिली आहे.
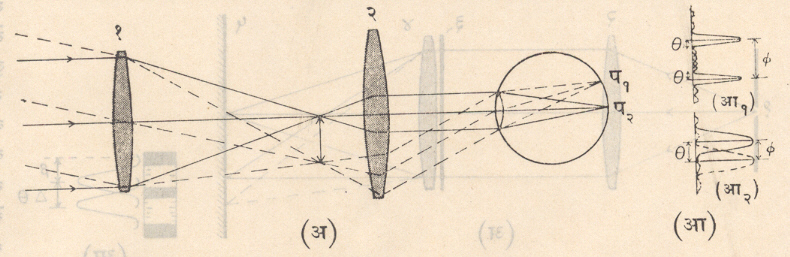
दूरदर्शक : समजा, स१ व स२ या दोन तेजस्वी वस्तू आहेत या वस्तू दूर असणारे दोन तारे असू शकतील किंवा दोन प्रकाशमान पदार्थ असतील. या वस्तू दूरदर्शकातून पाहिल्यास त्यांच्या दोन प्रतिमा प१ व प२
मिळतील. प१ व प२ मधील कोनीय अंतर f समजल्यास, प्रतिमांचा आकार कसाही असला, तरी हेच अंतर f त्यांच्या मध्यबिंदूंतील असते. कोणत्याही प्रकाशीय व्यूहाच्या मदतीने मिळणारी प्रतिमा प्रत्यक्षात फ्राउनहोफर विवर्तनाचा [योझेफ फोन फ्राउनहोफर या भौतिकीविज्ञांच्या नावाने ओळखल्या जाणाऱ्या विवर्तनाचा ⟶प्रकाशकी] परिणाम म्हणून मिळते. आयताकार फट वापरून प्राप्त होणाऱ्या फ्राउनहोफर विवर्तन
आकृतिबंधातील पहिल्या महत्तमातील व पहिल्या लघ्ज्ञुतमातील कोनीय अंतर θ असल्यास जोपर्यंत ϕ >> θ आहे, तोपर्यंत प्रतिमा भिन्न दिसतील. f = θ होता क्षणीच [रॅली कसोटी लॉर्ड रॅली या भौतिकीविज्ञांच्या नावाने ओळखली जाणारी कसोटी] प्रतिमा भिन्न दिसू लागण्याची सीमा गाठली जाते व तेव्हा एका प्रतिमेचा पहिला लघुत्तम दुसऱ्याच्या मध्य महत्तमावर पडतो (आ.१). गणिताने दाखविता येते की, अशा वेळेस दूरदर्शकाच्या बाबतीत विभेदन सीमा θपुढीलप्रमाणे असते.
θ =१·२२ λ/a … … … (२)
येथे λही प्रकाशाची तरंगलांबी असून, a ही आयताकार फटीची रुंदी आहे. समी. (२) वरून कळते, की दूरदर्शकाची विभेदन सीमा फटीच्या रुंदीच्या व्यस्त प्रमाणात वाढते (a व्यास असलेल्या गोलीय छिद्राच्या बाबतीतही हे विवेचन सर्वसाधारण रीत लागू पडते येथे a हा दूरदर्शकाच्या वस्तुभिंगाचा व्यास असतो). [⟶ दूरदर्शक].
सूक्ष्मदर्शक : वरीलप्रमाणे ⇨सूक्ष्मदर्शकाच्या बाबतीत अतिजवळ असलेल्या दोन वस्तूंतील विभेदनक्षम अंतर d येते, असे सिद्ध करता येते.
d= १·२२ λ/ २ N.A. … … (३)
समी. (३) मध्ये N.A. हा सूक्ष्मदर्शकाच्या वस्तुभिंगाचा संख्यात्मक छिद्रव्यास असून त्याचे मूल्य m sin α इतके असते, म्हणजेच वस्तू ज्या माध्यमात आहे. त्या माध्यमाचा प्रणमनांक m[प्रकाशाचा निर्वातातील कलावेग किंवा तरंगवेग व त्याचा निर्देशित माध्यमातील कलावेग यांचे गुणोत्तर ⟶ प्रकाशकी] व सर्वात दूरच्या किरणाने वस्तूतील अक्षस्थित बिंदूशी केलेल्या ‘कोनाची ज्या’ (म्हणजे sin α) यांच्या गुणाकाराइतके असते (म्हणजेच N.A. =m sin α). समी. (३) वरून स्पष्ट दिसते की, तरंगलांबी λशक्य तितकी कमी वापरून व शक्य तितका मोठा N.A. घेऊन सूक्ष्मदर्शकाची विभेदनक्षमता वाढविता येते. उदा., N.A. = १·०० व λ = ५३०० Ǻ(Ǻम्हणजे अँगस्ट्रॉम एकक Ǻ=१०-१० मी.) समजल्यास दर सेंमी.ला ३०,९४५ रेषा (दर इंचास ७८,६०० रेषा) इतके सूक्ष्म विभेदन होऊ शकते, तर तितक्याच N.A.मूल्यास λ = ४००० Ǻवापरता, विभेदन दर सेंमी.ला ४०,९४५ रेषा (दर इंचास १,०४,००० रेषा) म्हणजे सु. ३० टक्के अधिक मिळू शकते. वस्तू हवेत असल्यास N.A. चे अधिकतम मूल्य ०·९५ असते व मूल्यात λ/२ पेक्षा कमी विभेदन मिळू शकत नाही पण तैलनिमज्जन वापरल्यास (सूक्ष्मदर्शकाचे वस्तुभिंग व परीक्ष्य वस्तू यांच्या दरम्यान काचेइतकाच प्रणमनांक असलेल्या तेलाचे पातळ पटल वापरल्यास) N.A. चे अधिकतम मूल्य १·४ होते व म्हणून अधिकांश विभेदन मिळू शकते. [⟶सूक्ष्मदर्शक].
इलेक्ट्रॉन सूक्ष्मदर्शक : [⟶ इलेक्ट्रॉन सूक्ष्मदर्शक]. याच्या बाबतीत V विद्युत् वर्चसामुळे वेगयुक्त झालेल्या इलेक्ट्रॉनाची तरंगलांबी λ =१२·२६/ √V, Ǻअसते V = १५,००० व्होल्ट समजल्यास λ= ०·१ Ǻव हे तरंग वापरता समी. (३) प्रमाणे विभेदनक्षमता ०·६१ x ०·१/ ०·०१ Ǻ (N.A.= ०·०१) म्हणजे जवळजवळ ६ Ǻयेते. जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील) तरंग वापरलेल्या (λ =१००० Ǻ) प्रकाशीय सूक्ष्मदर्शकाच्या १०,००० पट इलेक्ट्रॉन सूक्ष्मदर्शकाची विभेदनक्षमता असते. ६Ǻहे मूल्य सैद्धांतिक आहे. प्रत्यक्षात ही विभेदनक्षमता जास्तीत जास्त २०Ǻअसते.
विवर्तन जालक : याच्या संबंधातही रॅली कसोटी लागू पडते. म्हणजे एका तेजस्वी वर्णपट रेषेचा मध्य महत्तम तितकीय तेजस्विता असलेल्या दुसऱ्या रेषेच्या पहिल्या लघुतमावर पडला असता, त्या दोन रेषा भिन्नत्वाने जेमतेम दिसू लागतात (आ.२). अशा स्थितीत त्या दोन रेषांच्या तरंगलांब्यातील (λआणि λ +Dλयांतील) फरकDλअसल्यास विवर्तन जालकाची विभेदनक्षमता.
λ /Dλ = nN … …. …. (४)
येते यात N ही जालकातील आखलेल्या रेषांची संख्या असून n हा वर्णपअ क्रमांक दर्शवितो. समी.(४) वरून दिसते की, N वाढविल्यास Dλकमी होतो व विभेदनक्षमता वाढते म्हणजे विभेदन होणाऱ्या दोन वर्णपट रेषांच्या तरंगलांब्या अधिक जवळ येतात. λ =६००० Ǻ, N=१०,००० व n=१ (पहिल्या क्रमांकाचा वर्णपट) समजल्यास
Dλ = λ/N = ०·६ Ǻ
[⟶विवर्तन जालक].
संदर्भ : 1.Ditchburn, R. W. Light, London, 1963.
2. Jenkins, F.A. White, H.E. Fundamentals of Optics, New York, 1976.
3. Stone,J.M. Radiation and Optics, New York, 1963.
भावे, श्री. द.
“