विद्युत् जालक सिद्धांत

विद्युत् जालक सिद्धांत : विद्युत् रोधक, कुंडल,क धारित्रे व ऊर्जा उद्‌गम यांसारख्या घटकांची जोडणी करून बनविलेल्या परस्पराशी निगडीत अशा अनेक विद्युत् मडळांना मिळून विद्युत् जालक म्हणतात. या घटकांशी निगडित असलेले विद्युत् प्रवाह, विद्युत् दाब व संरोध यांच्यातील संबंधांचे संश्लेषण (समन्वय) व सामान्यीकरण (व्यापकीकरण) करणे हे विद्युत् जालक सिद्धांतात अपेक्षित असते.

विद्युत् जालकाचे घटक: हे घटक सक्रिय आणि अक्रिय प्रकारचे असतात. जे घटक ऊर्जा पुरवितात ते सक्रिय घटक होत. सक्रिय घटकांचे पुढील दोन उपप्रकार आहेत : (१) निरवलंबी (उदा., विद्युत् घट वा घटमाला) अशा घटकांच्या अग्रांमधील विद्युत् दाब अथवा त्यांनी पुरविलेला विद्युत् प्रवाह हा मंडलामधल्या इतर सक्रिय घटकांच्या विद्युत् दाब किंवा विद्युत् प्रवाहावर अवलंबून असतो.

सक्रिय घटक दोन प्रकारे निदर्शित करता येतात : (१) विद्युत् दाब उद्‌गम व (२) विद्युत् प्रवाह उद्‌गम.

विद्युत् दाब उद्‌गम : आदर्श विद्युत् दाब उद्‌गमाच्या दोन अग्रांमधील विद्युत् दाब किंवा वर्चोभेद त्यापासून जालकामध्ये जाणाऱ्या विद्युत् प्रवाहावर अवलंबून नसतो. व्यवहारात उद्‌गामाला स्वतःचा अंतर्गत रोध असतो. त्यामुळे वास्तव उद्‌गमाच्या अग्रांमधील वर्चोभेद त्यातून वाहणाऱ्या विद्युत् प्रवाहावर अवलंबून असतो. अर्थात आदर्श विद्युत् दाब उद्‌गमाचा अंतर्गत रोध शून्य असतो.

विद्युत् प्रवाह उद्‌गम : आदर्श विद्युत् प्रवाह उद्‌गम जालकाला स्थिर विद्युत् प्रवाहाद्वारे ऊर्जा पुरवितो परंतु प्रत्यक्ष व्यवहारात उद्‌गमाला स्वतःचा अंतर्गत रोध असल्यामुळे जालकात जाणारा विद्युत् प्रवाह हा अग्रांमधील विद्युत् दाबावर अवलंबून असतो. अंतर्गत रोध अनंत असला तरच जालकातून वाहणारा विद्युत् प्रवाह उद्‌गमाच्या अग्रांमधील विद्युत् दाबावर अवलंबून राहणार नाही. आदर्श विद्युत् प्रवाह उद्‌गमाचा अंतर्गत रोध अनंत असतो. अशा प्रकारे वास्तव उद्‌गम हा आदर्श उद्‌गम आणि अंतर्गत रोध यांच्या संयोगाद्वारे दर्शविता येतो.

ट्रायोड व्हॉल्व्ह हा विद्युत् दाब नियंत्रित उद्‌गम आहे, तर ट्रँझिस्टर हा विद्युत् प्रवाह नियंत्रित उद्‌गम आहे. इलेक्ट्रॉनीय मंडलांत निर्वात नलिका किंवा ट्रँझिस्टर वापरतात. अशा मंडलांचे विश्लेषण करण्यासाठी अवलंबी उद्‌गमाच्या प्रतिकृतीचा उपयोग करतात.

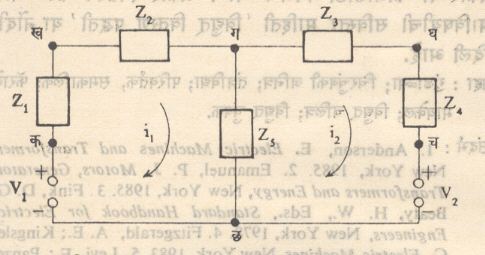विद्युत् जालाकामध्ये ज्या बिंदूवर दोन किंवा अधिक घटक जोडलेले असतात त्या बिंदूला जोड (नोड) व ज्या बिंदूवर तीन किंवा अधिक घटक एकत्र जोडलेले असतात त्या जोडाला संधिस्थान म्हणतात. घटकांचा व्याप एका जोडापासून दुसऱ्यापर्यंत असतो. दोन लगतच्या जोडांमध्ये असलेल्या घटकांच्या साखळीला विद्युत् जालकाची शाखा म्हणतात. तिच्यात एक वा एकसरीत जोडलेले अनेक घटक असतात. ज्यातून विद्युत् प्रवाह वाहू शकेल अशा एका (एकल) मार्गाला वलय अथवा मंडल म्हणतात. अंतर्गत शाखा नसणाऱ्या वलयाला जाळे वा गवाक्ष म्हणतात. आ. १ मध्ये क, ख, ग, घ, च, छ, ही संधिस्थाने असून खग, गघ, गछ, इ. शाखा आहेत. V₁, V₂ हे विद्युत् दाब उद्‌गम आहेत व कख, खग, गघ इ. अक्रिय घटक आहेत. कखगछक आणि गघचछग ही वलये आहेत. i, Z व V अक्षरे अनुक्रमे विद्युत् प्रवाह, संरोध व विद्युत् दाब दर्शवितात.

किरखोफ नियम : मंडलाच्या भिन्न घटकांतून वाहणाऱ्या विद्युत् प्रवाहाचे गणन करण्यासाठी ⇨ गुस्टाफ रोबेर्ट किरखोफ यांच्या पुढील दोन नियमांचा उपयोग करतात. (१) कोणत्याही संधिस्थानाकडे येणाऱ्या विद्युत् प्रवाहांची बेरीज शून्य असते. (२) कोणत्याही वलयामधील घटकांच्या अग्रांमधील विद्युत् दाबांची बेरीज शून्य असते.

प्रत्येक घटकाच्या बाबतीत V=RI हा ओहम नियम लागू असतो. (येथे V= विद्युत् दाब, R = विद्युत् रोध व I = विद्युत् प्रवाह आहे). हा नियम प्रत्येक क्षणी लागू होत असल्यामुळे उलटसुलट बदलत असणाऱ्या विद्युत् प्रवाहाच्या (प्रत्यावर्ती विद्युत् प्रवाहाच्या) बाबतीत लागू पडतो. प्रत्यावर्ती विद्युत् प्रवाहासाठी रोध R च्या ऐवजी त्या घटकाचा संरोध (एकूण विरोध) Z वापरावा लागतो म्हणजे वरील समीकरण V=ZI असे होते.

या विवेचनात हे गृहीत आहे की, मंडलातील सर्व घटक रेषीय (एकघाती) आहेत. म्हणजे रोधक, प्रवर्तक आणि धारित्र यांचे मूल्य त्यावर लावलेल्या विद्युत् दाबावर अथवा त्यामधून वाहणाऱ्या विद्युत् प्रवाहावर अवलंबून नसून ते स्थिर असते. जालकात अवलंबी उद्‌गम असले, तर त्यांचा विद्युत् दाब किंवा विद्युत् प्रवाह हा नियंत्रक विद्युत् दाब अथवा विद्युत् प्रवाह यांना समानुपाती (प्रमाणात) असतो, असे मानतात. अशा घटकांनी बनलेले विद्युत् मंडल रेषीय मंडल असते. व त्यासाठी लिहिण्यात येणारी समीकरणे एकघाती असतात.

काही प्रसंगी घटकांचे मूल्य स्थिर नसते. ते घटकावर लावलेल्या विद्युत् दाबावर किंवा त्यातून वाहणाऱ्या विद्युत् प्रवाहावर अवलंबून असते. असे घटक अरेषीय (नैकघाती) असतात. अशा घटकांचे बनलेले मंडल अरेषीय असते. त्यांच्यासाठी लिहिलेल्या नैकघाती समीकरणे सोडविणे अतिशय कठीण असते. अशा प्रसंगी जालकावर स्थापित केलेला संदेश लहान आहे, असे समजून रेषीय विश्लेषणाचा अवलंब करतात.

किरखोफ नियमांच्या आधारे आ. १ मधील प्रत्येक जोड व संधिस्थानासाठी आणि प्रत्येक शाखेसाठी समीकरणे लिहिली, तर त्यांची संख्या मोठी होते. ही संख्या कमी करण्याची युक्ती ⇨जेम्स क्लार्क मॅक्सवेल यांनी शोधून काढली. त्यांनी असे दाखवून दिले की. प्रत्येक संधिस्थानासाठी विद्युत् प्रवाहाचे समीकरण लिहिण्याऐवजी वलयात वाहणाऱ्या वर्तुळाकार विद्युत् प्रवाहांची (आ.१) कल्पना केल्यास समीकरणांची संख्या कमी होते.

विद्युत् जालकाच्या सिद्धांतातील समीकरणे सोडविण्यासाठी काही सामान्य रीती उपलब्ध आहेत परंतु एकंदरीत आकडेमोड (गणन) सुलभ करण्यासाठी खालील प्रमेये उपयोगी पडतात.

अध्यारोपण प्रमेय : एखाद्या जालकामध्ये अनेक उद्‌गम (सक्रिय घटक) असेल, तर कोणत्याही उद्‌गमाद्वारे कोणत्याही घटकात वाहणारा विद्युत् प्रवाह इतर उद्‌गमांवर अवलंबून नसतो. अर्थात कोणत्याही घटकात वाहणारा एकूण विद्युत् प्रवाह प्रत्येक उद्‌गमामुळे त्या घटकातून वाहणाऱ्या विद्युत् प्रवाहाच्या बेरजेएवढा असतो.

एखाद्या घटकातून वाहणाऱ्या विद्युत् प्रवाहाचे गणन करण्यासाठी त्या जालकात एका वेळी एकच उद्‌गम आहे अशी कल्पना करून त्याच्यामुळे घटकात वाहणाऱ्या विद्युत् प्रवाहाचे गणन करतात. असे करताना इतर उद्‌गम जालकातून काढून घेऊन त्यांच्या जागी त्यांचा अंतर्गत रोध किंवा संरोध प्रतिष्ठापित करतात. हीच क्रिया क्रमशः इतर उद्‌गमांच्या बाबत करावयाची उदा., आ. १ मध्ये गछ मधून वाहणारा विद्युत् प्रवाह काढण्यासाठी एकदा V₂ हा उद्‌गम काढून घेऊन तो मंडल संक्षेपित करून V₁ मुळे गछ मधून किती विद्युत् प्रवाह वाहतो याचे गणन करतात नंतर हा उद्‌गम काढून टाकून ते मंडल संक्षेपित करून या उद्‌गमामुळे गछ मधून किती विद्युत् प्रवाह वाहतो याचे गणन करतात म्हणजे V₁ आणि V₂ या दोन्ही उद्‌गमांद्वारे गछ मधून वाहणारा विद्युत् प्रवाह वरील दोन विद्युत् प्रवाहांच्या बेरजेएवढा होईल. १० व्होल्ट उद्‌गमाद्वारे गछ मधून वाहणारा विद्युत् प्रवाह (४०/२३) अँपिअर,तर २० व्होल्ट उद्‌गमाद्वारे गछमधून वाहणारा विद्युत् प्रवाह (३०/२३) अँपियर आहे. म्हणून दोन्ही उद्‌गम असताना गछ मधून एकूण (७०/२३) अँपिअर विद्युत् प्रवाह वाहील.

थेवेनिन प्रमेय : हे प्रमेय फ्रेंच अभियंते लेआँ थेवेनिन (१८२७-१९२६) यांनी १८८३ साली. मांडले. अनेकदा जालकामधील एखाद्या अक्रिय घटकामधून वाहणारा विद्युत् प्रवाह गणन करावयाचा असतो अशा प्रसंगी विचारधीन अक्रिय घटक वगळून इतर सर्व घटक एका पेटीत बंद केले आहेत अशी कल्पना करतात. या पेटीच्या आत असलेल्या जालकाच्या संरचनेविषयी सविस्तर माहिती असण्याची आवश्यकता नसते म्हणून या पेटीला काळी पेटी म्हणतात. तथापि पेटीमध्ये असलेल्या जालकाऐवजी असे साधे सुटसटीत जालक ठेवता येते की, जे विचाराधीन अक्रिय घटकाला जोडले की, त्यावरील विद्युत् दाब आणि त्यातून वाहणारा विद्युत् प्रवाह यांत फरक पडणार नाही. हे जालक म्हणजे पूर्वीच्या जालकाचे सममूल्य (समतुल्य) जालक होय. या कल्पनेप्रमाणे आ. १ खालीलप्रमाणे दर्शवावी लागते (आ.२).

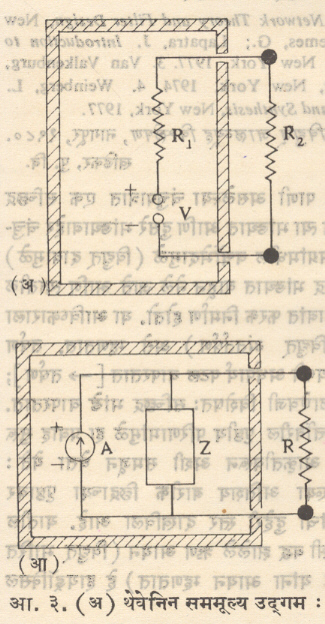थेवेनिन प्रमेयानुसार अक्रिय घटकाला जोडलेल्या मंडलाच्या सममूल्य उद्‌गमाचा विद्युत् दाब घटक काढून टाकल्यानंतर त्या अग्रांमधील विद्युत् दाबाएवढा असतो व त्या उद्‌गमाचा अंतर्गत रोध किंवा संरोध मंडलातील सर्व उद्‌गम काढून टाकून त्यांच्या जागी त्यांचे अंतर्गत रोध किंवा संरोध प्रतिष्ठापित केले, तर त्या अग्रांमध्ये असलेल्या रोधाएवढा अथवा संरोधाएवढा असतो.

आ. २ मधील ग व छ मधील २ ओहमचा रोध काढून घेऊन ती अग्रे खुली केली, तर त्यांमधील विद्युत् दाब

व्होल्ट असतो.

आतील दोन्ही उद्‌गम मंडल संक्षेपित केले, तर पेटीतील मंडलाचा रोध २४/११ ओहम होतो. अर्थात गछ या अक्रिय घटकाला जोडलेल्या मंडलाच्या सममुल्य मंडलातील उद्‌गमाचा विद्युत् दाब १४०/११ व्होल्ट व त्याच्या एकसरीत असणारा रोध २४/११ ओहम असतो. याला त्या मंडलाचा थेवेनिन सममूल्य उद्‌गम म्हणतात.

R₂= ओहम 

 या प्रमेयासाठी अट अशी की, गछमधील अक्रिय घटकामध्ये इतर कोणत्याही घटकात वाहणाऱ्या विद्युत् प्रवाहामुळे अथवा विद्युत् दाबामुळे विद्युत् प्रवाह अथवा विद्युत् दाब निर्माण होऊ नये अर्थात एका मंडलातून दुसऱ्या मंडलात ऊर्जा संक्रमण करणारा परस्परसंबंध असू नये, म्हणजेच गछमधील अक्रिय घटकाचे दुसऱ्या कोणत्याही घटकाशी युग्मन असू नये.

नॉर्टन प्रमेय : (आ. ३). हे थेवेनिन प्रमेयाचे द्वैत स्वरूप आहे. अक्रिय घटकाला जोडलेल्या मंडलाच्या सममूल्य उद्‌गमाचा प्रवाह, तो घटक काढून घेऊन मंडलाची अग्रे जोडली, तर त्यातून वाहणाऱ्या विद्युत् प्रवाहएवढा असतो व त्या उद्‌गमाची संवाहिता ही मंडलातील सर्व उद्‌गम काढून टाकून त्यांच्याऐवजी त्यांचे अंतर्गत रोध किंवा संरोध प्रतिष्ठापित केले, तर त्या अग्रांमधील संवाहितेएवढी असते. आ. २ मधील ग आणि छ या अग्रांमधील २ ओहमचा रोध काढून ती अग्रे मंडल संक्षेपित केली, तर किरखोफ नियमांचा उपयोग करून गणित केल्यास त्यामधून वाहणारा विद्युत् प्रवाह (३५/६) अँपिअर असल्यास आढळते. ग आणि छ अग्रांकडून पेटीकडे पाहिल्यास व पेटीतील उद्‌गमांऐवजी त्यांचा अंतर्गत रोध (जो शून्य आहे) ठेवल्यास संवाहिता

सीमेन्स (म्हो) असल्याचे आढळते. म्हणून मंडलाचा सममूल्य उद्‌गम ३५/६ अँपिअर विद्युत् प्रवाह देतो व त्याची समांतर संवाहिता ११/२४ सीमेन्स आहे. या प्रमेयाचा उपयोग करताना गछमधील अक्रिय घटकाचे वरीलप्रमाणे दुसऱ्या कोणत्याही घटकाशी युग्मन नको ही अट पाळली पाहिजे.

जालकाविषयीचे प्रश्न सोडविण्यासाठी वरील प्रमेयांव्यतिरिक्त इतर प्रमेयांचा देखील उपयोग करतात, पण वर निर्देशिलेली प्रमेये सर्वांत महत्त्वाची आहेत.

इतिहास : भौतिकी, गणित व अभियांत्रिकी या विज्ञानक्षेत्रांतील माहितीच्या एकत्रीकरणातून विद्युत् जालक सिद्धांत पुढे आला आहे. त्यामुळे या प्रत्येक क्षेत्रातील प्रगतीचा फायदा या सिद्धांताच्या प्रगतीला झाला आहे. या दृष्टीने किरखोफ यांचे विद्युत् मंडलांविषयीचे कार्य महत्त्वाचे आहे, तर व्होल्ट-अँपिअर संबंधाद्वारे विद्युत् जालकातील घटकांची वैशिष्ट्ये ठरविण्याकरिता गेओर्क झिमोन ओहम, मायकेल फॅराडे व जेम्स क्लार्क मॅक्सवेल यांचे कार्य आधारभूत ठरले आहे.

विद्युत् जालकाविषयीच्या पुष्कळ संकल्पना रूढ गतिकीमधून आलेल्या आहेत. सर विल्यम आर्, हॅमिल्टन व झोझेफ ल्वी लाग्रांझ यांच्या भौतिकी व गणित या विषयांतील गतिकीविषयक कार्याची विद्युत् जालक सिद्धांत विकसित होण्यास मदत झाली आहे.

जालक विश्लेषण व जालक संश्लेषण ही विद्युत् जालक सिद्धांताची दोन अंगे आहेत. जालक विश्लेषणात दिलेल्या माहितीवरून एका विवक्षित घटकावरील विद्युत् दाब व त्यातून वाहणारा विद्युत् प्रवाह यांचे गणन करतात, म्हणजे यामध्ये एखादी प्रणाली तीवर लावलेल्या उद्दीपकाला कशा प्रकारे प्रतिसाद देते, याचा अभ्यास करतात, जॉर्ज ए. कॅम्बेल या गणितज्ञांनी विसाव्या शतकात जालक विश्लेषणात महत्त्वाचे मूलभूत कार्य केले आहे.

जालक विश्लेषणाच्या तुलनेने जालक संश्लेषणाचे क्षेत्र हे अधिक अलिकडे विकसित झाले आहे आणि जालक संश्लेषण सिद्धांताच्या मुळाशी जालक विश्लेषणामधील संकल्पना आहेत. जालक संश्लेषणाची सरुवात रिअँक्टन्स थेअरम (१९२४) या रॉनल्ड एम्. फॉस्टर याच्या पुस्तकापासून झाली. विवक्षित प्रकारे कार्य करणाऱ्या विद्युत् जालकाचा अभिकल्प (आराखडा) तयार करणे, जालक संश्लेषणाचे उद्दिष्ट असते. फॉस्टर यांच्या संशोधनामुळे प्रयत्न-प्रमाद पद्धतीने काम करण्याची गरज राहिली नाही आणि विशेष प्रकारचे जालक कसे बांधावे, याविषयीची निश्चित कार्यपद्धती समजली, योसिरो ऊनो, व्हिल्हेल्म कानेर, एडवर्ड एल् नॉर्टन, एर्न्स्ट ए. गेयमँ, सिडनी डार्लिंग्टन, रोन फिअल्कोव्ह, राऊल बॉट रिचर्ड जे. डफीन इ. संशोधकांनीही जालक संश्लेषणाविषयीचे महत्त्वपूर्ण संशोधन केले. पिलोटी व डार्लिंग्टन यांनी स्वतंत्रपणे संशोधन करून एकसारखे निष्कर्ष काढले व ते जवळजवळ एकाच वेळेस प्रसिद्ध झाले, त्यांच्या या संशोधनामुळे अचूक विद्युत् छानकांचे [गाळण्यांचे ⟶छानक, विद्युत्] आधुनिक अभिकल्प तयार करणे शक्य झाले, तारांच्या एकाच जोडीमागे अनेक संदेश प्रेषित करणारी संवह दुरध्वनिविद्या, रेडिओ व दूरचित्रवाणी प्रेषण, रडार इत्यादींत असे छानक अतिशय महत्त्वाचे असतात.

या आधीचे संशोधन हे अक्रिय जालकांच्या संश्लेषणाविषयीचे होते. बाह्य उद्‌गमापासून पुरविलेल्या विजेपेक्षा जास्त वीज देऊन शकणाऱ्या विद्युत् जालकांना अक्रिय जालक म्हणतात, तर विजेचे विविरर्धन करू शकणाऱ्या जालकांना सक्रिय जालक म्हणतात. या क्षेत्रात हेंड्रिक डब्ल्यू. बोडे व हॅरी नायक्विस्ट या दोघांनी १९२०-३० व १९३०-४० या दशकांत संशोधन केले. यांशिवाय आडोल्फ हुर्विट्झ ई. जे. राऊथ आलेक्सांद्र एम्. ल्यापूनोव्ह वगैरेंनीही या क्षेत्रात संशोधन केले होते.

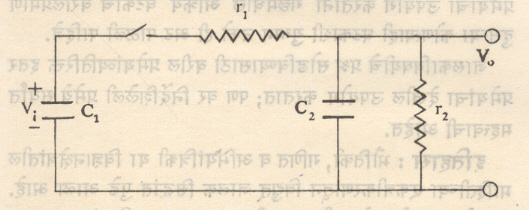उपयोग : विद्युत् अभियांत्रिकी, संदेशवहन, अवकल सिद्धांत, वस्तूंची वाहतूक इ. क्षेत्रांमध्ये विद्युत् जालक सिद्धांताचा उपयोग होतो. एवढेच नव्हे, तर औषधिविज्ञानासारख्या क्षेत्रातदेखील या सिद्धांताचा उपयोग होतो. उदा., औषध असलेला द्रव पदार्थ शरीरात रक्तप्रवाहात सोडला, तर त्या औषधाची रक्तातील संहती (प्रमाण) कालाप्रमाणे कशी बदलत जाईल, ती महत्तम केव्हा होईल अशा प्रश्नांची उत्तरे माहीत असणे औषधोपचाराच्या दृष्टीने आवश्यक असते. रोग्यांवर प्रत्यक्ष प्रयोग करणे शक्य नसते आणि इष्टही नसते. त्यामुळे ही माहिती मिळविण्यासाठी या प्रक्रियेतील घटनांचा विचार करून त्यांच्याशी अनुरूप किंवा सदृष विद्युत् जालक बांधतात. उदा,. आ. ४ मध्ये C₁ धरित्र औषध असलेल्या द्रवाचे आकारमान दर्शविते, तर औषधी द्रवाला रक्तात जाताना होणारा विरोध r₁ ने दर्शिविला आहे. C₂ धरित्र रक्तप्रवाहाचे आकारमान दर्शविते. R₂ हो वृक्क (मूत्रपिंड) इ. उत्सर्जन यंत्रणेचा निदर्शक आहे. V_i औषधाच्या मात्रेची संहती दर्शवितो, तर V_o या जालकाच्या प्रदानाद्वारे रक्तप्रवाहातील औषधाचे प्रमाण समजते. या जालकातील घटकांची मूल्य सहज बदलून भिन्न परिस्थितीत जालकाच्या वर्तनाचा सविस्तर व सखोल अभ्यास करून त्याच्या आधारे योग्य औषधयोजना करता येते.

ज्या जालकाद्वारे संदेशाचे विवर्धन होते त्यांना सक्रिय जालक म्हणतात. त्यांत ट्रँझिस्टर, निर्वात नलिका इ. सक्रिय घटक असतात. जालकाच्या प्रदानातील काही अंश आदान म्हणून वापरून जालकाची संवेदनशीलता व कार्यप्रवणता (कार्यमान वैशिष्ट्ये) वाढविता येते. या घटनेला पश्चभरण म्हमतात. अशा पश्चभरण जालकांचा स्वयंचालन नियंत्रक वगैरेंमध्ये बहुमोल उपयोग होतो. उदा., औद्योगिक प्रक्रियांच्या स्वयंचालनासाठीच्या निंयंत्रणांचा अभिकल्प करण्याच्या दृष्टीने विद्युत् जालक सिद्धांत महत्त्वाचा आहे.

विद्युत् अभियांत्रिकी आणि इलेक्ट्रॉनिकीमध्ये जालक सिद्धांत अतिशय उपयोगी ठरला आहे. याशिवाय ध्वनिकी, प्रकाशकी, यामिकी वगैरेंमध्ये जालक सिद्धांताद्वारे मिळालेल्या माहितीचा वापर करता येतो. यामुळे तपशीलाच्या किचकट बाबींना फाटा देऊन अतिशय गुंतागुंतीच्या यामिकीय, ध्वनिकीय व विद्युतीय परिस्थितींचे विश्लेषण करणे शक्य झाले आहे. जालक सिद्धांतातील आदान-प्रदान, काळी पेटी, पश्चभरण इ. संकल्पनांमुळे जीवविज्ञान आणि अर्थशास्त्र यांना एक नवा दृष्टिकोण मिळवून दिला आहे.

उच्च वेगाने अंकीय संगणक पुढे आले. त्यांच्यात पूर्वी विद्युत् जालक छानक व नियंत्रक म्हणून वापरीत. आता याच कामांसाठी विद्युत् जालकांऐवजी अंकीय जालक वापरतात. अंकीय जालकाचे घटक वेगळे असून त्यांच्यातील आदान-प्रदान संख्यांच्या द्विमानसांकेतिक श्रेणी असतात. यांपैकी एका प्रकारच्या जालकाच्या विश्लेषणाला व अभिकल्पाला लागू पडणारा सिद्धांत हा दुसऱ्या प्रकारच्या जालकाला लागू करण्यायोग्य रूपात बदलता येतो.

पहा : एकदिश विद्युत् प्रवाह विद्युत् मंडल विद्युत् मंडल परीक्षण.

संदर्भ :1. Aatre, V. K. Network Theory and Filter Design, New York, 1980.

       2. Temes, G. Laptra, J. Introduction to Circuit synthesis, New York, 1977.

      3. Van valkenburg, Network Analysis, New York, 1974.

      4. Weiberg, L. Network Analysis and synthesis, New York, 1977.

     ५. केळकर, आ. रा. विद्युत् जालव्यूह विश्लेषण, नागपूर, १९८०.

खांडेकर, पु. वि.

“