वर्चस्

वर्चस् : विश्वातील कोणत्याही दोन जड वस्तूंमध्ये मिळणाऱ्या  विविध प्रक्रियांचा अभ्यास केला, तर त्यांचे वर्गीकरण पुढील मूलभूत प्रकारांपैकी एक किंवा अधिक परस्परक्रियांच्या रूपात करता येते, असे आढळते : (१) गुरुत्वीय, (२) विद्युत् चुंबकीय, (३) दुर्बल अणुकेंद्रीय व (४) प्रबल अणुकेंद्रीय.

गुरुत्वीय परस्परक्रिया जड वस्तूंच्या द्रव्यमानांमुळे कार्यान्वित होते, तर विद्युत् चुंबकीय परस्परक्रिया त्यांवरील विद्युत् भारांमुळे निर्माण होत असते. दोन जड वस्तूंमध्ये कोणतेही मध्यस्थ माध्यम नसतानासुद्धा गुरुत्वीय व विद्युत् चुंबकीय परस्परक्रिया आढळून येतात. याच्या स्पष्टीकरणाकरिता गुरुत्वाकर्षणीय किंवा विद्युत् चुंबकीय क्षेत्र या कल्पना पुढे आल्या. या संकल्पनेप्रमाणे (उदा., गुरुत्वाकर्षणीय परस्परक्रिया विशद करण्याकरिता) द्रव्यमान असणाऱ्या  प्रत्येक जड वस्तूभोवती दूर अंतरापर्यंत पसरलेले असे एक गुरुत्वीय क्षेत्र प्रथम अस्तित्वात येते, असे मानले जाते. दुसरी वस्तू व त्या ठिकाणी अस्तित्वात असणारे क्षेत्र यांमघ्ये परस्परक्रिया प्रत्यक्षात निर्माण होत असते. क्षेत्रामधील कोणत्याही बिंदूपाशी असणाऱ्या क्षेत्राचे संपूर्ण वर्णन त्या ठिकाणी एकक द्रव्यमान मूल्याचा कण ठेवला असता त्यावर मिळणाऱ्या  प्रेरणेच्या तीन (X, Y, Z अक्ष दिशांतील) घटक मूल्यांचा निर्देश करून देता येते.

विद्युत् चुंबकीय क्षेत्राचे पर्यायी वर्णन करण्याकरिता अदिश वर्चसाची संकल्पना प्रथम सिमेआँ देनिस प्वासाँ (१७८१-१८४०) व जॉर्ज ग्रीन (१७९३-१८४१) यांनी उपयोगात आणली. एखाद्या प्रणालीमध्ये संग्रहित केलेल्या विद्युत् ऊर्जेचे मूल्य (खालील सूत्रानुसार) तीमधील विद्युत् भाराच्या रेषीय प्रमाणात असते.  

वर्चस् =   विद्युत् ऊर्जा/ विद्युत्  भार  

ही विद्युत् ऊर्जा अव्यक्त स्वरूपातच असते म्हणून तिला इंग्रजी भाषेतील या अर्थाची संज्ञा (potential) देण्यात आली.

क्षेत्राचे निर्देशन करण्याकरिता अवकाशातील भिन्न बिंदूंपाशी असणारी क्षेत्र तीव्रतेची तीन घटक मूल्ये (उदा.,X, Y, Z दिशांतील) देण्याऐवजी त्या ठिकाणच्या वर्चस् मूल्याचे निर्देशन पुरेसे होते. गणितीय सूत्राचा उपयोग करून वर्चस् चलनापासून प्रेरणा घटक मूल्ये अवकलन क्रियेने [⟶ अवकलन व समाकलन] मिळविणे अवघड नाही पण ही क्रिया करण्याकरिता x, y, z व t या सहनिर्देशकांचे वर्चस् हे संतत फलन असून त्यामध्ये कोणत्याही ठिकाणी एकाकी विसंगती, खंड किंवा अनंतता यांची अनुपस्थिती आवश्यक असते [⟶ फलन].

क्षेत्राचे निर्देशन करण्याकरिता वर्चसाचा उपयोग करण्यामध्ये दोन फायदे असतात : (१) वर्चस् अदिश असल्यामुळे कोणत्याही दोन किंवा अधिक क्षेत्रांमुळे निर्माण होणाऱ्या परिणामी वर्चसाचे गणितीय दृष्ट्या गणन करणे सोपे होते. (२) कोणत्याही क्षेत्रात अनेक वेळा एका ठराविक जागी वस्तू असता तिच्याजवळ किती मूल्याची ऊर्जा आहे, हे प्रयोग करून (उदा., अणुकेंद्रीय विक्रिया) निश्चित करता येते. त्यावरील प्रेरणेचे अशा सरळपणे मापन करता येत नाही. त्यामुळे वर्णन करण्याकरिता निरीक्षण करता येईल अशा राशीची निवड अधिमान्यतेने करणे योग्य दिसते.

सगळ्या भौतिकीय प्रणालींकरिता वर्चसाच्या साहाय्याने सर्व प्रकारच्या क्षेत्रांचे निर्देशन करून त्यापासून क्षेत्र-प्रेरणा-मूल्ये मिळविणे शक्य होत नाही.  ज्या प्रणालीकरिता हे शक्य असते, अशा प्रणालीला स्थितिरक्षक प्रणाली असे म्हणतात. ज्या प्रणालीमध्ये ही प्रक्रिया शक्य होत नाही तिला व्यय प्रणाली असे म्हणतात. या दोन प्रणाली प्रकारांमधील भेद खालील उदाहरणावरून स्पष्ट होईल.

अनेक कणांपासून बनलेला एक समूह लक्षात घेऊ. या सर्व कणांवर विद्युत् भार आहेत असे मानले, तर त्यामुळे या सर्व कणांमध्ये परस्परक्रिया निर्माण होतील, हे स्पष्ट आहे. यांपैकी एक विद्युत् भारवाही कण अ येथे उपस्थित असून तो  हालचाल करू शकतो, तर बाकीचे सर्व विद्युत् भारवाही कण आपआपल्या ठिकाणी अचल किंवा स्थिर आहेत, असे मानू. अ येथील कणांवर मिळणाऱ्या परिणामी प्रेरणेचे मूल्य समूहातील इतर कणांवरील विद्युत् भार व त्यांची चल कणापासून असणारी अंतरे यांवर अवलंबून राहते. अ येथील कण हा समूह प्रणालीपासून अनंत अंतरावर नेला असता समूहातील विद्युत् भारित कणांचा परिणाम शून्य मूल्याचा असेल असे गृहीत धरले, तर तेथील वर्चस् मूल्य शून्य आहे, असे समजण्यास हरकत नाही. एकक विद्युत् भार असलेला चल कण अनंतापासून अ या स्थानबिंदूपर्यंत क्षेत्र प्रेरणेच्या विरुद्ध दिशेत आणण्याकरिता जे कार्य करावे लागते ते व्याख्येप्रमाणे क्षेत्रामुळे अ या ठिकाणी निर्माण झालेल्या विद्युत् वर्चसाचे मूल्य देते. हे संचारण करण्याकरिता अनंतापासून अ पर्यंत पोहचणारा कोणताही गतिमार्ग वापरला, तरी चालतो, त्यामुळे वर्चस् निश्चितीमध्ये काहीही फरक पडत नाही. ज्या प्रणालीकरिता वरील विधान यथार्थ असते म्हणजे जिच्याकरिता अनंतापासून अ स्थानबिंदूपर्यंत विद्युत् भार हालविण्याकरिता करावे लागणारे कार्य हे फक्त विद्युत् भाराच्या प्रारंभिक व अंतिम स्थानबिंदूवरच अवलंबून असते, अशा प्रणालीला स्थितिरक्षक प्रणाली असे म्हणतात. अशा प्रणालीकरिता कोणत्याही एका स्थानबिंदूपासून सुरुवात करून कोणत्याही मार्गाने एकाकी विद्युत् भाराला परत त्याच ठिकाणी आणल्यास परिणामी करावे लागणारे कार्यमूल्य शून्य असते. स्थितिरक्षक प्रणालीकरिताच वर्चसापासून गणितीय रीत्या प्रेरणा मूल्ये काढता येतात.

वर्चसाच्या व्याख्येमध्ये विद्युत् भारित कण क्षेत्र प्रेरणेच्या विरुद्ध दिशेत संचारण करीत आहे असे मानले असल्यामुळे याकरिता करावे लागणारे कार्य हे कणाजवळ स्थितिज ऊर्जेच्या स्वरूपात राहते, असा अर्थ होतो. खरोखरी पाहता ही स्थितिज ऊर्जा सबंध प्रणालीजवळ संचयित केली जाते. चल कणावरील विद्युत् भार जर अल्प प्रमाणाचा असेल आणि त्याच्या हालचालीमुळे क्षेत्रामधील स्थिर विद्युत् भार वितरणावर जर विशेष परिणाम होत नसेल, तर  ही स्थितिज ऊर्जा चल कणाजवळच संग्रहित होते, असे आसन्नपणे (अंदाजे) मानता येते.

वर्चस् व क्षेत्र प्रेरणा यांमधील संबंधांची सूत्रे : विद्युत् क्षेत्रमधील (x, y, z)या सहनिर्देशकांनी निर्देशित केलेल्या बिंदुस्थानी वर्चस् जर∅एवढे असेल, तर त्या बिंदूपाशी असणाऱ्या क्षेत्र तीव्रतेचे घटक खालील सूत्राने मिळतात (स्थितिरक्षक प्रणालीकरिता) :

EX = –

∂∅  ∂ X

,

EY = –

∂∅  ∂ y

,

Ez = –

∂∅  ∂ z

…   …  (1)

किंवाE = – grad ∅ = -Ñ.∅ ………(२)

Grad वÑया चिन्हांच्या स्पष्टीकरणासाठी ‘सदिश’ ही नोंद पहावी).

 

कोणत्याही (x, y, z) या क्षेत्रबिंदूजवळ असणारे वर्चस् मूल्य खालील सूत्राने मिळते.

या गणितीय अटीचे पालन केले जाते कारण कोणत्याही बंदिस्त गतिमार्गाकरिता परिणामी कार्य शून्य मूल्याचे असते.  

स्थितिक विद्युत् वर्चस् : ज्या प्रणालीमध्ये एक किंवा अधिक स्थिर विद्युत् भार आहेत, जिच्यामध्ये विद्युत् भाराचे मूल्य कालानुसार बदलत नाही, जिच्यामध्ये विद्युत् प्रवाह वहात नाहीत अशा परिस्थितीतील प्रणालीमध्ये स्थितिक विद्युत् क्षेत्र मिळते.

या प्रकारच्या सर्वांत सोप्या उदाहरणातील प्रणालींमध्ये एकच स्थिर Q मूल्याचा बिंदू विद्युत् भार असतो. कुलंब नियमाप्रमाणे या विद्युत् भारामुळे त्यापासून r अंतरावर जे स्थितिक विद्युत् क्षेत्र E निर्माण होते, त्याचे मूल्य [सयुक्तिक एकक पद्धतीप्रमाणे ⟶ एकके व परिमाणे] खालील सूत्राने मिळते.

⟶	=	Q	…   …   (५)
E		4 π∈ r2

 येथे ∈ =  विद्युत् भाराभोवती असणाऱ्या  माध्यमाकरिता असणारा विद्युत् अपार्यता स्थिरांक आहे.

वर दिलेल्या सूत्राचा उपयोग करून विद्युत् वर्चस् 

∅r = –	Q	…   …   (६)
	4 π∈ r

असे दाखविता येते. विद्युत् भार बिंदूपासून r या अंतरावर असणाऱ्या r क्षेत्रबिंदूपाशी असणारे वर्चस् मूल्य∅rयाचिन्हाने निर्देशित होते. प्रत्यक्षात विद्युत् क्षेत्र किंवा असणारे वर्चस् हे (१) अवकाशात निरनिराळ्या ठिकाणी प्रस्थापित केलेले बिंदुमात्र विद्युत् भार, (२) पदार्थाच्या पृष्ठभागावर पसरलेला विद्युत् भार व (३) घनफळामध्ये वितरित झालेला विद्युत् भार या तीन प्रकारे निर्माण होऊ शकते, त्यामुळे सर्वसामान्य परिस्थितीकरिता वर्चस्

या सूत्राने मिळते. यामध्ये s = विद्युत् भाराची क्षेत्रफळ घनता, p =  विद्युत् भाराची घनफळ घनता,  ds =  क्षेत्रफळाचे प्राथमिक एकक, dv =  घनफळाचे प्राथमिक एकक.

ज्या भौतिकीय परिस्थितीमध्ये फक्त घनफळ वितरित असा विद्युत् भार उपस्थित असतो, तीकरिता [मॅक्सवेल समीकरणांवरून ⟶ मॅक्सवेल विद्युत् चुंबकीय समीकरणे]

∇2 ∅ = –	ρ	…   …   (८)
	ϵ

हे प्वासाँ समीकरण मिळते, तर ज्या प्रणालीमध्ये मुक्त विद्युत् भार नसतात तीकरिता

Ѳ∅=   0                 …                 …       (९)

हे लाप्लास समीकरण मिळते.  

ज्या विद्युत् भारांमुळे विद्युत् क्षेत्र निर्माण होते, ते विद्युत् भार ज्या स्थानविभागात उपस्थित असतात अशा अवकाश विभागाकरिता प्वासाँ समीकरण सार्थ ठरते. या अवकाश विभागाच्या बाहेरील सर्व क्षेत्र बिंदू स्थानांकरिता लाप्लास समीकरण यथार्थ असते.

विद्युत् क्षेत्र मूल्याचे त्याच्या उगम विद्युत् भाराबरोबर रेषीय चलन होत असल्यामुळे निरनिराळ्या विद्युत् भारांमुळे निर्माण होणाऱ्या क्षेत्रांचे एकमेकांवर अध्यारोपण करणे शक्य होते. अध्यारोपण तत्त्वाची यथार्थता गृहीत धरूनच ∅ करिता वर दिलेले (७) हे सूत्र मांडले आहे.

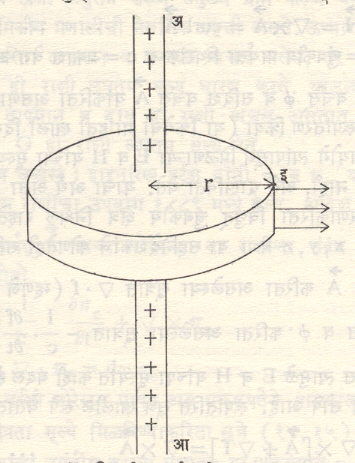
लॉगरिथमीय वर्चस् : स्थितिक विद्युत् वर्चसाकरिता मिळणारे हे एक वैशिष्ट्यपूर्ण उदाहरण आहे. अआ ही दंडगोलाकार (त्रिज्या = a) विद्युत् भारित तार असून तिच्या प्रती लांबी एककावर l मूल्याचा विद्युत् भार आहे. तारेच्या अक्षापासून r अंतरावर असणाऱ्या इ या क्षेत्रबिंदूपाशी मिळणारे  (r) हे वर्चस् खालील सूत्राने मिळते, हे दाखविता येते.

∅ (r)  = l/2p∊ log r + ∝ …        (१०)

जर r &gt  &gt   a अ,स. तर येथे ∊ = परिसर माध्यमाचा विद्युत् पार्यता स्थिरांक व ∝= सीमा अटींमुळे निश्चित होणारा स्थिरांक आहेत. 

चुंबकीय अदिश वर्चस्Y : जेव्हा विद्युत् व चुंबकीय क्षेत्रे कालानुसार बदलत नाहीत, तेव्हा त्यांमध्ये परस्परसंबंध नसतो. अशा परिस्थितीत स्थिर विद्युत् भारामुळे विद्युत् क्षेत्र निर्माण होत असते, तर शाश्वत चुंबके किंवा विद्युत् चुंबक यांद्वारे चुंबकीय क्षेत्र निर्माण केले जाते. अशा विद्युत् व चुंबकीय क्षेत्रांमध्ये परस्परसंबंध काहीच नसतो व त्याची मूल्ये दोन स्वतंत्र अदिश वर्चसांपासून मिळतात :

---

φ= (x,y,z) या क्षेत्रबिंदूकरिता चुंबकीय अदिश वर्चस्. चुंबकीय क्षेत्र H मॅक्सवेल समीकरणाचे पालन करीत असल्यामुळे

विद्युत् चुंबकीय वर्चसे : जेव्हा चुंबकीय क्षेत्र H व विद्युत् क्षेत्र E या राशी कालानुसार बदलतात व त्यांचा परस्परसंबंध मॅक्सवेल समीकरणाने दिला जातो, तेव्हा  त्याचे निर्देशन निव्वळ अदिश वर्चसाच्या स्वरूपात करणे शक्य होत नाही. या परिस्थितीचा भौतिकीय अर्थ असा असतो की, बदलत्या E मुळे  H याची निर्मिती होत असते, तर बदलत्या H मुळे  E क्षेत्र निर्माण होत असते.

अशा परिस्थितीमध्ये या दोन क्षेत्रांचे मूल्य निश्चित करण्याकरिता अदिश वर्चस्   व सदिश वर्चस A^→ या दोन्ही राशींचा उपयोग केला जातो. फ्रांट्स नॉयमन यांनी सदिश वर्चस् कल्पनेचा वापर १८४५ मध्ये प्रथम  केला. A^→ व    यांमधील परस्परसंबंध खाली दिलेल्या सूत्रांमुळे मिळतो.

येथे m = चुंबकीय पार्यता स्थिरांक व c = प्रकाश वेग आहेत.

अदिश वर्चस् ∅ व सदिश वर्चस् A^→ यांकरिता असणाऱ्या सूत्रांवर मापक-रूपांतरण क्रिया( या क्रियेची माहिती खाली दिली आहे) केल्यास त्यायोगे त्यांपासून मिळणाऱ्याच E व H यांच्या मूल्यांत काही फरक पडत नाही, असे दाखविता येते. याचा अर्थ असा होतो की, या रूपांतरणाकरिता विद्युत् चुंबकीय क्षेत्र निश्चल राहते. उदा., ‘f’ हे जर x, y, z व t या सहनिर्देशकांचे कोणतेही सदिश फलन असेल, तर Aकरिता असलेल्या सूत्रात Ñ.f (म्हणजे grad f ) मिळविल्यास व ∅ करिता असलेल्या सूत्रात

–	1	.	∂f
	c		∂f

 ही राशी मिळविल्यास त्यामुळे E व H यांच्या मूल्यांत काही बदल होत नाही, हे दाखविणे सोपे आहे. रूपांतरित सूत्रे खालील रूपे घेतात.

रूपांतरण होते, त्यास मापक-रूपांतरण असे म्हणतात. मॅक्सवेल क्षेत्र समीकरणे मापक-रूपांतरणाकरिता निश्चल राहतात. रूपांतरणाकरिता हेंड्रिक आंटोन लोरेन्ट्स यांनी सुचविलेली आणखी एक सुसंगत आणि अनुज्ञात अशी गणितीय अट घातल्यास A^→ व ∅ यांमधील संबंध जास्त स्पष्ट होतो. लोरेन्ट्स यांची अट खालील सूत्राने निर्देशित केली जाते.

या अटीचा वापर केल्यास (यास लोरेन्ट्स मापक-रूपांतरण म्हणतात) 

असे दाखविता येते. वरील सूत्राचा उपयोग केल्यास  

हे सूत्रसंबंध मिळविता येतात. त्यामुळे अदिश व सदिश वर्चस् सूत्रांमधील साम्य स्पष्ट होते.  

काल-प्रतिगामी विद्युत् चुंबकीय वर्चसे : विद्युत् भाराला दोन अंगे असतात, असे वरील विवेचनावरून स्पष्ट होते. विद्युत् भाराचे अवकाशातील वितरण p या राशीने निर्देशित केले जाते. विद्युत् भाराचे कालानुसार चलन हे माध्यमातील विद्युत् प्रबाह घनता राशी (J) ने निर्देशित होते, स्थिर विद्युत् भार वितरणामुळे फक्त विद्युत् क्षेत्रे निर्माण होऊ शकतात. विद्युत् भार गतिमान होऊन त्यामुळे विद्युत् प्रवाह निर्माण झाले की, त्यामुळे प्रथम चुंबकीय क्षेत्र H व त्यामुळे ¶E/¶t (ज्यामुळे विद्युत् क्षेत्रामधील बदल दाखविला जातो) अशी दोन्ही चलने मिळू लागतात. विद्युत् भाराचा गतिवेग स्थिर नसून त्यामध्ये प्रवेगामुळे बदल होत असेल, तर या परिस्थितीमध्ये विद्युत् चुंबकीय क्षेत्राचे प्रारणाच्या (तरंगरूपी ऊर्जेच्या) स्वरूपात प्रसारण होते. या प्रक्रियेचे वर्णन करण्याकरिता काल-प्रतिगामी वर्चसाचा उपयोग करावा लागतो.

---

या प्रक्रियेमागील भौतिकीय संकल्पनेचे विवरण खालील सुलभ रीतीने करता येते. प्रारण प्रसारणाच्या अ  या उगम स्थानी विद्युत् भार वितरण p व विद्युत् प्रवाह घनता J या दोन राशी कालाप्रमाणे बदलत आहेत, असे समजू. या राशींत होणाऱ्या  बदलांमुळे उगमस्थानापासून r अंतरावर दूर असणाऱ्या आ या क्षेत्रबिंदूपाशी असलेल्या विद्युत् व चुंबकीय क्षेत्रांत तदनुरूप बदल होणे आवश्यक होते. याबाबतचा संदेश उगमापासून निघून आ या क्षेत्रबिंदूपर्यंत c या सांत (परिमित) प्रकाशवेगाने प्रगत होतो, असे दाखविता येते. त्यामुळे कोणत्याही t या क्षणी उगमस्थानी p व J या राशी तदनुसार नवी मूल्ये धारण करतात पण त्या क्षणी आ येथे असणारी प्रत्यक्ष परिस्थिती उगमस्थानाच्या (t-r/c)  या कालबिंदूनुसारच असणार, हे उधड आहे. उदा., तेथील विद्युत् वर्चस् मूल्य  t कालबिंदूनुसार नसून ते (t-r/c ) या कालक्षणाच्या अनुरूप असते. या वर्चसाला काल-प्रतिगामी वर्चस् अशी संज्ञा दिली जाते. याविषयीचे विश्लेषण ए. लिनार्ड (१८९८) व ई. विखर्ट (१९००) यांनी प्रथम केले असल्यामुळे काल-प्रतिगामी वर्चसांना लिनार्ड-विखर्ट वर्चसे असे पण म्हणतात. या प्रतिगामी वर्चसांच्या आधारे विद्युत् चुंबकीय क्षेत्रे प्रारणाच्या स्वरूपात कशी प्रसारित केली जातात, हे विशद करता येते.

e हा बिंदू विद्युत् भाराचा इलेक्ट्रॉन जेव्हा v या स्थिर वेगाने मार्गक्रमण करतो, तेव्हा त्याच्यापासून R अंतरावर असणाऱ्या  क्षेत्रबिंदूपाशी लिनार्ड-विखर्ट वर्चस् मूल्ये मिळतात, असे दाखविता येते.

येथे ε = विद्युत् पार्यता स्थिरांक, m= चुंबकीय पार्यता स्थिरांक, R = इलेक्ट्रॉन स्थानबिंदू व क्षेत्रबिंदू यांना जोडणारा त्रिज्या सदिश व c = प्रकाश वेग.

ही कल्पना अधिक स्पष्ट करण्याकरिता उगम स्थानी (r = 0) कालानुसार प्रत्यावर्ती बदल दाखविणारा विद्युत् भार q = q₀e^jait आहे असे समजू. बदलाची कंप्रता = ω/2p. या विद्युत् भारापासून खूप अंतरावर (r) असणाऱ्या विद्युत् वर्चसाकरिता खालील सूत्र मिळविता येते.

सूत्रामध्ये kहा स्थिरांक आहे. वरील सूत्रातील पहिले पद काल-प्रतिगामी लिनार्ड-विखार्ट वर्चस् दर्शविते. वरील सूत्रावरून एकाच वेळी मिळणारी उगमस्थानाजवळील परिस्थिती व क्षेत्रबिंदूजवळील परिस्थिती यांमध्ये कसा फरक असतो, हे स्पष्ट होते. एका दाखल्यावरून वरील विवेचनातील मध्यवर्ती कल्पना स्पष्ट होईल. आपण जेव्हा आकाशाकडे पाहतो तेव्हा चंद्र व दूरवरचे तारे यांना एकाच वेळी पाहू शकतो पण ताऱ्यापासून प्रकाश किरणांना पृथ्वीपर्यंत येण्याकरिता कित्येक वर्षे लागतात. तर प्रकाशास चंद्रापासून पृथ्वीपर्यंत येण्यास काही सेकंद लागतात. त्यामुळे दूरच्या ताऱ्याचे जे स्वरूप आज दिसते ते त्याच्या अनेक वर्षांपूर्वीच्या स्वरूपाचे निर्देशन करीत असते, हे स्पष्ट असते. याउलट चंद्राच्या जवळजवळ सध्याच्या स्वरूपाचे दर्शन घडत असते.

गुरुत्वीय वर्चस् : एकक द्रव्यमानाची जड वस्तू गोलीय सममिती असणाऱ्या M द्रव्यमानाच्या जड वस्तूपासून r अंतरावर ठेवली, तर आयझॅक न्यूटन यांच्या मीमांसेप्रमाणे त्या दोहोंमध्ये एक आकर्षणी प्रेरणा मिळते व तिचे मूल्य खालील सूत्राद्वारे मिळते.

F = –  GM/r² …         …              ..           (२५)

येथे G = गुरुत्वीय स्थिरांक आहे.

क्षेत्र सिद्धांतानुसार ही प्रेरणा वर्चसाच्या स्वरूपात मांडता येते. M द्रव्यमानाच्या जड वस्तूमुळे r अंतरावर मिळणारे वर्चस् (∅)

∅  = –     GM/r                    …         …              ..          (२६)

या सूत्राने मिळते. m द्रव्यमान असणाऱ्या  जड वस्तूवर निर्माण होणारी प्रेरणा

F_m = –  m∇.∅                      …         …              ..          (२७)

या सूत्राने मिळते. जर जड वस्तू गोलीय आकाराची नसेल, तर तीकरिता पुढील सूत्र वापरता येते.

∅ = –   G⨛pdV/r                      …         …              ..     (२८)

येथे ρ = द्रव्यमान घनता व dV = प्राथमिक घनफळ आहे.

वेग वर्चस् : द्रायू (वायू किंवा द्रव) माध्यम जर सरळ रेषेत गतिमान होत असेल अथवा त्यांचे संचारण सुप्रवाही व भोवरेरहित असे असेल, तर त्याच्या गतीचे वर्णन करण्याकरिता∅या वेग वर्चसाचा उपयोग केला जातो. 

अशा संचारणामध्ये द्रायू माध्यमाचा वेग v^→ हा स्थानानुसार बदल दाखवितो. माध्यमातील( x,y,z) या स्थानबिंदूपाशी त्याचा वेग v^→ मूल्याचा असेल , तर वेग वर्चस् खालील सूत्रानुसार निश्चित होते.

v = – ∇.∅                           …               …           …        (२९)

जर द्रायू असंकोच्य असून त्याने स्थिर गतिस्थिती प्राप्त करून घेतली असेल, तर सातत्य अटीप्रमाणे ∇. v = 0∇ हे दाखविता येते, म्हणून अशा द्रायूकरिता ∇².∅ = 0 हे लाप्लास सदृश्य समीकरण यथार्थ ठरते. 

ऊष्मागतिकीय वर्चस् : ऊष्मागतिकीय मीमांसेमध्ये हेल्महोल्ट्स फलन F व गिब्ज फलन G यांना ऊष्मागतिकीय वर्चसे अशी संज्ञा दिली जाते [⟶ ऊष्मागतिकी]. ही फलने खालील समीकरणांच्या साहाय्याने निर्देशित केली जातात.

F = U-TS = U + T ( δF/δT)_v …          (३०)

G = U-TS  + PV             …     …           (३१)

यांतील अक्षरचिन्हांच्या स्पष्टीकरणासाठी ‘ऊष्मागतिकी ’ ही नोंद पहावी.

या फलनाचे ⇨यामिकीमधील वर्चसाबरोबर एका बाबतीत साम्य आहे. स्थितिज ऊर्जा लघुतम करून संतुलन प्राप्त करून घेण्याकडे कोणत्याही यामिकीय प्रणालीची नैसर्गिक प्रवृत्ती असते. ऊष्मागतिकीतील प्रणालींकरिता तापमान व घनफळ अचल असेल, तर संतुलन अवस्थेमध्ये F ही राशी लघुतम मूल्य धारण करते. याउलट ज्या प्रणालीकरिता तापमान व दाब या राशी अचल असतात, तेव्हा संतुलनाकरिता G ही राशी लघुतम मूल्य घेते.

---

ध्रुवीकरण वर्चसे : हाइन्रिख हर्ट्झ यांनी π_e व π_m या दोन ध्रुवीकरण वर्चस् राशींचा उपयोग १८८९ मध्ये केला. अदिश वर्चस् ∅ व सदिश वर्चस् A^→ याच्याबरोबरचा या राशींचा संबंध पुढील सूत्रांनी स्पष्ट होतो. 

A =  I/c.  δp_e /δt   + ∇ X p_m …      (३२)

∅  = – ∇. p_e =    dωp_e …             (३३)

p_e व p_m ही वर्चसे लोरेन्ट्स मापन अट एकरूपतेने पाळतात. E व B ही क्षेत्र तीव्रता मूल्ये मिळविण्याकरिता सूत्रे (१४, १५) आणि (३२,३३) यांचा उपयोग करावा लागतो. या प्रक्रियेमध्ये p_e व p_m या राशींच्या द्वितीय अवकलजांचा [⟶ अवकलन व समाकलन] वापर आवश्यक ठरतो.

डेबाय वर्चसे : एकविध व समदिक् अशा माध्यमांमध्ये जर स्थानीकृत उद्गमांचे वितरण असेल (उदा., हवेत धूलिकणांची उपस्थिती), तर त्याद्वारे विद्युत् चुंबकीय तरंगांचे प्रारण किंवा प्रकीर्णन (विखुरणे) यांपैकी कोणतीही प्रक्रिया होऊ शकते (उदा., हवेतील वायुकणांमुळे सूर्यप्रकाशाचे प्रकीर्णन झाल्यामुळे आकाशाला निळा रंग येतो). या प्रक्रियांचे वर्णन करण्याकरिता p_e व p_m अशा दोन अदिश वर्चस् फलनांचा वापर करावा लागतो, असे पेट्रस डेबाय यांनी १९०९ मध्ये दाखविले म्हणून या वर्चस् राशींना डेबाय वर्चसे असे म्हणतात.

रासायनिक वर्चस् : ऊष्मागतिकीय प्रणालीमध्ये सामान्यपणे अनेक (एकाहून अधिक) रासायनिक घटक असतात. प्रणालीमध्ये फक्त k प्रकारच्या रासायनिक द्रव्याचे जर n_k ग्रॅम मोल (कोणत्याही पदार्थाच्या ग्रॅममधील रेणवीय द्रव्यमानाएवढ्या द्रव्यमानाला ग्रॅम मोल असे म्हणतात) उपस्थित असतील, तर या घटकाकरिता असणारे रासायनिक वर्चस् m_k खालील सूत्राने दिले जाते.  

m_k = δ G/δn_k

या सूत्रामध्ये G गिब्ज फलन. प्रणालीमध्ये k घटक प्रथमपासून उपस्थित नसला, तरी त्यामुळे  याचे मूल्य शून्य असले पाहिजेच, असे नाही. प्रावस्था संक्रमण व रासायनिक संतुलन या प्रक्रियांच्या गतिकीकरिता रासायनिक वर्चसाचा उपयोग होतो.

वर्चोभेद :समवर्चस् पृष्ठ: गुरुत्वीय व विद्युत् चुंबकीय क्षेत्रांच्या संदर्भात निरपेक्ष वर्चस् मूल्याला काही विशेष अर्थ असत नाही, हे नमूद करणे आवश्यक आहे. मापनाच्या दृष्टीने विचार करता फक्त दोन बिंदूंमधील वर्चोभेद (वर्चस् फरक) प्रत्यक्षात मोजता येतो. उदा., विद्युत् क्षेत्रामध्ये अ व आ या दोन बिंदूंमधील वर्चोभेद, आ या कमी मूल्याचे वर्चस् असलेल्या बिंदूपासून एकक विद्युत् भार अ या बिंदूपर्यंत नेण्यामध्ये जे कार्य करावे लागते त्याच्या स्वरूपात मोजला जातो. या हालचालीमध्ये जड वस्तूजवळ असणाऱ्या स्थितिज ऊर्जेमध्ये फरक पडतो. स्थितिज ऊर्जेकरिता सुद्धा निरपेक्ष शून्य मूल्य प्रमाण नसते. बहुतेक सर्व भौतिकीय प्रश्नांकरिता जड वस्तू अनंतापर्यंत नेली म्हणजे तिची स्थितिज ऊर्जा व वर्चस् मूल्य शून्य आहे, असे मानण्याचा संकेत आहे. याउलट विद्युत् मंडलामध्ये भूसंपर्क बिंदू हा वर्चसाकरिता शून्य मूल्य मानण्याचा प्रघात आहे.

गुरुत्वीय किंवा विद्युत् चुंबकीय क्षेत्रांकरिता त्रिमितीय अवकाशामध्ये एक वितरण मिळते. एकाच मूल्याचे वर्चस् असणाऱ्या सर्व क्षेत्रबिंदूंमधून जर एक पृष्ठ काढले, तर त्यास समवर्चस् पृष्ठ असे म्हणतात. क्षेत्रामध्ये जर परीक्षा वस्तू ठेवली, तर तिच्यावर असणाऱ्या प्रेरणेच्या दिशेत ती संचारण करू लागते (विद्युत् चुंबकीय क्षेत्राकरिता परीक्षा वस्तू ही एकक विद्युत् भार असलेली बिंदुमात्र वस्तूही होते). प्रेरणा दिशा रेषा ह्या समवर्चस् पृष्ठाला सर्वत्र लंब दिशेत छेदतात, असे दाखविता येते.

पहा : गुरुत्वाकर्षण मॅक्सवेल विद्युत् चुंबकीय समीकरणे क्षेत्र सिद्धांत.

संदर्भ : 1. Corson, D. Lorrain, p. Introduction to Electromagnetic Fields and Waves, San Francisco, 1962.

           2. Gupta, S.L. Singh, S. P. Kumar, V. Electricity and Magnetism and Classical  Electrodynamics, Meerut, 1972.

           3. Helms, H. L. Introduction to Potential Theory, Huntington, N. Y., 1975.

           4. Marrion, J. B. Classical Electromagentic Radiation, New York, 1965.

           5. Wermer, J. Potential Theory, Berlin, 1974.

चिपळोणकर, व. त्रिं.

“