वक्र

वक्र: [अ, ब] या अंतरालावर जर क्ष = क्ष (ट), य = य (ट), झ = झ (ट) या समीकरणांद्वारे तीन संतत फलने दिलेली असतील, तर त्यामुळे ट चलाची अवकाशातील फलन प्रतिमा (क्ष, य, झ) या कार्तीय सहनिर्देशकांनी निश्चित होईल [⟶फलन]. अशा प्रकारे [अ, ब] ची अवकाशातील मिळालेली प्रतिमा म्हणजे अवकाश वक्र. ट ला अ पासून ब पर्यंत निरनिराळी  मूल्ये क्रमाने देत गेल्यास वक्राच्या क या आरंभबिंदूपासून ख या अंत्यबिंदूपर्यंत अवकाशात क्रमाने बिंदूप्रतिमा मिळतात व त्यावरून क ते ख असा दिशायुक्त वक्र मिळतो, तो बिंदूपथ असतो. ट या चलाला प्रचल तर वरील समीकरणांना वक्राची प्रचल समीकरणे म्हणतात. ट ऐवजी क्ष, य, झ यांपैकी एक चलही प्रचलासाठी घेतात. अवकाश वक्राची अधिक माहिती ‘भूमिती’ या नोंदीतील ‘अवकल भूमिती’ या उपशीर्षकाखाली पहावी.

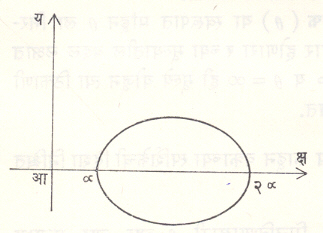
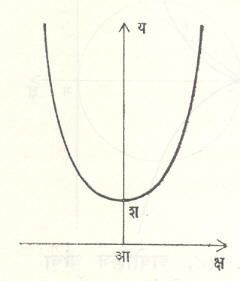
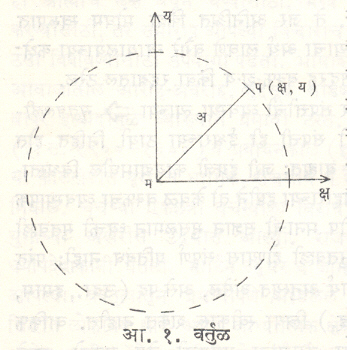प्रतल वक्र : याचे सर्व बिंदू एकाच प्रतलावर असतात. जर क्ष-अक्ष आणि य-अक्ष या प्रतलावर घेतले, तर क्ष हे प्रचल घेऊन क्ष = क्ष, य = य (क्ष), झ = ०, अ ≤ क्ष ≤ ब, अशी वक्राची समीकरणे लिहिता येतील. यातील क्ष = क्ष व झ = ० ही समीकरणे सर्वच वक्रांना लागू असल्याने ती गृहीत धरून लिहीत नाहीत. जर क्ष चे अंतराल दिलेले नसेल, तर य (क्ष) ही क्ष ची प्रतिमा ज्या क्ष च्या मूल्यांसाठी मिळविता येत असेल अशा सर्व मूल्यांचा संच अंतराल म्हणून गृहीत धरतात. क्ष व य मधील संतत फलनसंबंध फ (क्ष, य) = ० अशा समीकरणानेही दाखवितात. आ. १ मध्ये फ (क्ष, य) = क्ष^२ + य^{२ −} अ^२ = ० हा वक्र (वर्तुळ) दिला आहे.

प्रतलीय वक्राचे ध्रुवीय समीकरण फ (र, θ) = ० किंवा यावरून काढता येणारे र = र (θ) असे असते. मात्र र(θ) हे संतत फलन हवे. θ हा प्रचल घेऊन क्ष = र (θ) कोज्या θ, मात्र य = र (θ) ज्या θ अशी या वक्राची कार्तीय समीकरणे मिळतात. (‘भूमिती’ या नोंदीतील ‘वैश्लेषिक भूमिती’ हा भाग पहावा.)

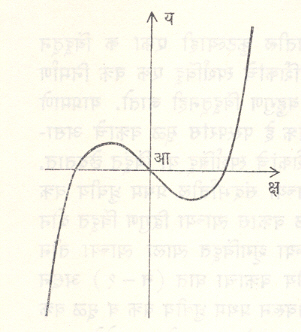
वक्राच्या स्पर्शिका व प्रलंब : प्रतल वक्राच्या अभ्यासात स्पर्शिकेला महत्त्वाचे स्थान आहे. क आणि ख हे वक्रावरील कुठलेही दोन बिंदू असल्यास कख रेषेस वक्राची जीवा म्हणतात. ख बिंदू क च्या अधिकाधिक जवळ आणल्यास सीमावस्थेत कख रेषा वक्रास क च्या ठायी स्पर्श करते. या वेळी कख ला वक्राची स्पर्शिका म्हणतात व क ला तिचा स्पर्शबिंदू म्हणतात (आ. २). स्पर्शबिंदूतून स्पर्शिकेला काढलेल्या लंब रेषेस वक्राचा प्रलंब म्हणतात.

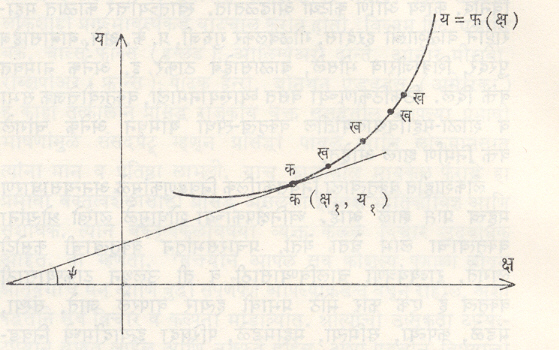
स्पर्शिकेने क्ष अक्षाच्या दिशेशी केलेला कोन ψ असल्यास स्प ψ या मूल्याला [⟶त्रिकोणमिति] त्या रेषेचा उतार म्हणतात. अवकलनशास्त्रानुसार dय/dक्ष या अवकलजाने स्पर्शिकेचा उतार काढता येतो [⟶ अवकलन व समाकलन], तो dय/dक्ष = फ’ (क्ष) असा लिहितात. म्हणूनच वक्राचे समीकरण य = फ (क्ष) असल्यास (क्ष_१, य_१) चे ठायी स्पर्शिकेचे समीकरण य–य_१ = फ’ (क्ष_१) (क्ष–क्ष_१) असे होईल. वक्राचे समीकरण फ (क्ष, य) = ० या स्वरूपात असल्यास स्पर्शिकेचे समीकरण (क्ष–क्ष_१)^.फ_क्ष (क्ष_१, य_१) + (य–य_१)^.फ_य (क्ष_१, य_१) = ० असे होईल. येथे फ_क्ष = ∂फ/∂क्ष आणि फ_य = ∂फ/∂य हे फ चे क्ष आणि य सापेक्ष आंशिक अवकलज आहेत. 

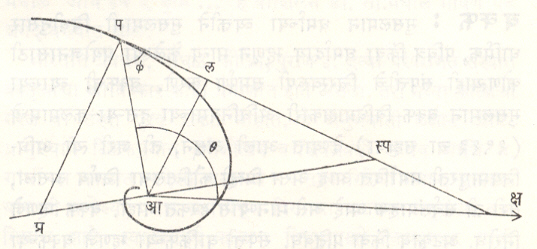
ध्रुवीय पद्धतीत स्पर्शबिंदू ध्रुवबिंदूशी जोडणारी रेषा व स्पर्शिका यांच्यातील कोन ø असल्यास स्प ø =र  dθ / dर असतो. त्यावरून र = फ (θ) या वक्राच्या स्पर्शिकेचे समीकरण उ = ऊ कोज्या (θ − ∝) + ऊ’ ज्या (θ − ∝) असे मिळविता येते.

येथे उ = १/र असून स्पर्शबिंदू (१/ऊ, ∝) आहे. तसेच ऊ’ हे dउ/ dθ चे या स्पर्शबिंदूच्या ठायी असलेले मूल्य आहे. (आ. ३).

याप्रमाणे प्रलंबाची समीकरणेही खालील स्वरूपात मिळतात.

वक्राचे समीकरण                                   प्रलंबाचे समीकरण

य = फ (क्ष)                                       क्ष–क्ष_१+फ’ (क्ष_१) (य–य_१) = 0

फ(क्ष, य)=0                            क्ष–क्ष_१/फ_क्ष (क्ष_१,य_१) = य– य_१/फ_य (क्ष_१,य_१) 

र=फ(θ)                                            ऊ’/ऊ  उ = ऊ’ कोज्या (θ–∝)

                                                                       –ऊ ज्या (θ–∝)

वक्राची दिशा त्याच्या बिंदूतून काढलेल्या स्पर्शिकांच्या साहाय्याने निश्चित करता येते. सामान्यतः वक्राच्या सर्व बिंदूंतून त्याला स्पर्शिका काढणे शक्य असल्याने त्याच्या कुठल्याही बिंदूतील त्याची दिशा ठरविता येते.

य = फ (क्ष) हा वक्र काढल्यास सर्वसाधारणपणे ज्या ठिकाणी फ (क्ष) महत्तम किंवा लघुतम असते, त्या ठिकाणी dय/dक्ष = 0 असते, म्हणजेच अशा ठिकाणी स्पर्शिका क्ष अक्षाला समांतर असते [⟶ अवकलन आणि समाकलन].

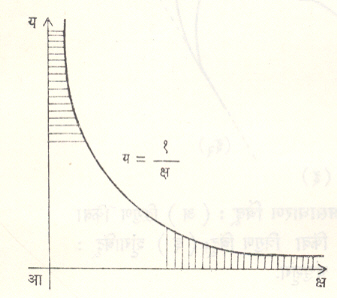
अमर्याद वक्राच्या बाबतीत स्पर्शिकेचा स्पर्शबिंदू अनंताप्रत जाऊ शकतो. जेव्हा अशी रेषा आदिबिंदूपासून परिमित अंतरावर असूनही वक्रास अनंताप्रत स्पर्श करते, तेव्हा तिला अनंतस्पर्शिका म्हणतात.

उदा., य = १/क्ष हा वक्र घेतल्यास क्ष = 0 आणि य = 0 ह्या (म्हणजेच अनुक्रमे य आणि क्ष अक्ष) त्या वक्राच्या अनंतस्पर्शिका होत. (आ. ४).

कधी कधी ध्रुवीय पद्धतीत दिलेल्या वक्राच्या समीकरणातील θ चे मूल्य अमर्यादपणे वाढवीत गेल्यास वक्राचे समीकरण वर्तुळ समीकरणाचे स्वरूप धारण करते. या समीकरणाने निर्देशिलेल्या वर्तुळास अनंतस्पर्शी वर्तुळ असे म्हणतात.

स्पर्शिका क्ष अक्षाला ज्या बिंदूत छेदते तो बिंदू आणि स्पर्शबिंदूतून क्ष अक्षावर काढलेल्या लंबाचा पादबिंदू यांच्यातील अंतरास अवस्पर्शिका असे म्हणतात; उदा., आ. ५ मधील स्पल. प्रलंबाचा क्ष अक्षावरील छेदनबिंदू आणि स्पर्शबिंदूतून क्ष अक्षावर काढलेल्या लंबाचा पादबिंदू यातील अंतरास अवप्रलंब असे म्हणतात; उदा., आ. ५ मधील प्रल. अवस्पर्शिकेची लांबी य/dय /dक्ष, तर अवप्रलंबाची लांबी य d य/ d क्ष या सूत्रांनी मिळते.

वक्रता : वक्राचा बाक मोजणारे माप म्हणजेच वक्रता होय. उदा., वक्रवरील क आणि ख या दोन निकटच्या बिंदूंतील स्पर्शिका क्ष अक्षाशी अनुक्रमे ψ व ψ+δψ हे कोन करीत असल्यास त्यावरून त्यांच्यामधील कोन = δψ मिळतो. हाच कोन स्पर्शिकेच्या दिशेतील कख अंतरात निर्माण झालेला बदल दर्शवितो. δψ/ δस (δस = क आणि ख यांमधील वक्राची लांबी) या गुणोत्तरास सरासरी वक्रता म्हणतात. येथे ख बिंदू क च्या निकट आणल्यास या गुणोत्तराचे सीमान्त मूल्य म्हणजेच वक्राची क बिंदूतील वक्रता होय (आ. ६) म्हणजेच वक्रता = सीमा δस⟶०  δψ/ δस = dψ/ dस 

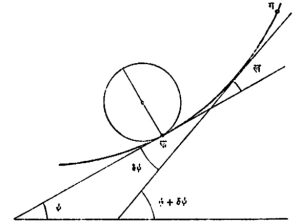
वर्तुळाबाबत वक्रतेचे मूल्य १/त्रिज्या एवढे म्हणजेच स्थिरांक असते. याचा उपयोग करूनही वक्राची वक्रता ठरविता येते. त्यासाठी वक्रावरील क, ख, ग या तीन बिंदूंतून जाणारे एक वर्तुळ कल्पितात. ख आणि ग हे बिंदू क च्या ठायी एकत्रित झाल्यास मिळणारे या वर्तुळाचे सीमान्त स्वरूप वक्रतेचे वर्तुळ या नावाने संबोधले जाते. या वर्तुळाच्या त्रिज्येस वक्रतेची त्रिज्या असे म्हणतात. वक्राची क बिंदूतील वक्रता ही (१/त्या बिंदूतील वक्रतेची त्रिज्या) एवढी असते. यामुळेच वक्र जसजसा अधिक बाक घेतो तसतसे वक्रतेचे वर्तुळ लहान लहान होत जाते, तर वक्रता वाढत जाते.

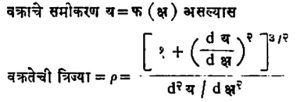
इतर सहनिर्देशक पद्धतींमध्येही वक्रता त्रिज्येची सूत्रे मांडता येतात.

वक्रतेचे वर्तुळ मिळविताना त्या वर्तुळाला आणि वक्राला समाईक असे तीन बिंदू (क, ख, ग) एकत्रित येत असल्याने ते वर्तुळ वक्राला क येथे स्पर्श करते म्हणजेच या बिंदूतून वक्र व वर्तुळ या दोहोंनाही स्पर्श करणारी समान स्पर्शिका काढता येते.

वक्रतेच्या वर्तुळाचा मध्य वक्रता मध्य या नावाने ओळखला जातो. वक्रावरील क, ख, ग या बिंदूतून वक्राला काढलेले प्रलंब ख आणि ग बिंदू क च्या ठायी एकत्रित झाल्यावर सीमास्थितीत वक्रतेच्या वर्तुळाच्या त्रिज्येचे स्वरूप धारण करतात. यामुळेच वक्रतेचा मध्य हा वक्रावरील प्रलंबाच्या छेदनबिंदूंची सीमास्थिती काढूनही मिळविता येतो. कार्तीय पद्धतीत याचे सहनिर्देशक पुढीलप्रमाणे मिळतात.

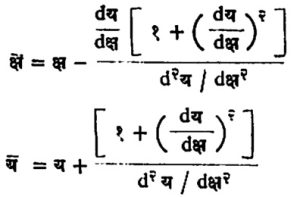
भ्रमणबिंदूचे  वक्रावरील भ्रमण चालू असता वक्रतेचे वर्तुळ व सोबत वक्रतेचा मध्यही फिरत असतो. वक्रता मध्याच्या या भ्रमणातून निर्माण झालेला वक्र म्हणजेच वक्रता मध्याचा बिंदुपथ यास मूळ वक्राचा उद्वलित म्हणतात. याउलट मूळ वक्रास या बिंदुपथाचा आवलित म्हणतात. एका बिंदुपथास असे अनंत आवलित (उदा., क’ ख’ ग’ … .) मिळविता  येतात. मूळ वक्रावरील कुठल्याही दोन बिंदुंतील वक्रता त्रिज्यांच्या लांबीतील फरक हा उद्वलितावरील संगत बिंदुंमधील चापलांबीएवढा असतो. उद्वलिताच्या वक्रतेची त्रिज्या d²स / dψ^२ असते.

वक्रकुल : अन्वालोप व उद्विलित : वक्राच्या समीकरणात चलपदांबरोबर काही वेळा प्रचलपदे (विशिष्ट परिस्थितीत स्थिर मूल्ये धारण करणारी पदे) असतात. उदा., फ (क्ष, य, अ) = ० या वक्राच्या समीकरणात अ हे प्रचलपद आहे. या प्रचलपदाची अनेक मूल्ये आहेत असे गृहीत धरल्यास त्या प्रत्येक मूल्याला एक याप्रमाणे अनेक वक्र मिळतात. याप्रमाणे मिळणाऱ्या वक्रांच्या समूहास वक्रकुल असे म्हणतात. येथे अ चे मूल्य एका विशिष्ट वक्रापुरतेच स्थिर असते.

जो वक्र दिलेल्या वक्रकुलाच्या प्रत्येक घटकास स्पर्श करतो आणि ज्याच्या प्रत्येक बिंदूत एक तरी घटक वक्र त्याला स्पर्श करून जाते त्यास त्या वक्रकुलाचा अन्वालोप म्हणतात. अन्वालोप हा क्रमागत वक्रांच्या छेदनबिंदुंचा बिंदुपथ असतो (आ. ८). याचे समीकरण

फ (क्ष, य, अ) = ० ; ∂/ ∂अ  — फ (क्ष, य, अ) = ०

या दोन समीकरणांतून अ या प्रचलाचा निरास केल्यास सम्यक समीकरण मिळते. अवकल समीकरणात पूर्ण निर्वाहाला वक्रकुल मानल्यास त्याचा अन्वालोप समीकरणाचा एकमात्र निर्वाह दाखवतो. [⟶अवकल समीकरणे].

वक्रतेचा मध्य हा वक्रावरील क्रमागत बिंदूंतून काढलेल्या प्रलंबांच्या छेदनबिंदूंची सीमास्थिती असल्याने प्रलंबांचा अन्वालोप अशी उद्वलिताची व्याख्या करतात. तसेच ⇨द्वित्व तत्त्वानुसार दोन निकटच्या स्पर्शिकांचा छेदनबिंदू सीमास्थितीत त्यांतील एकीच्या स्पर्शबिंदूत पोहोचत असल्याने स्पर्शिकांचा अन्वालोप अशी वक्राची व्याख्या करता येते.

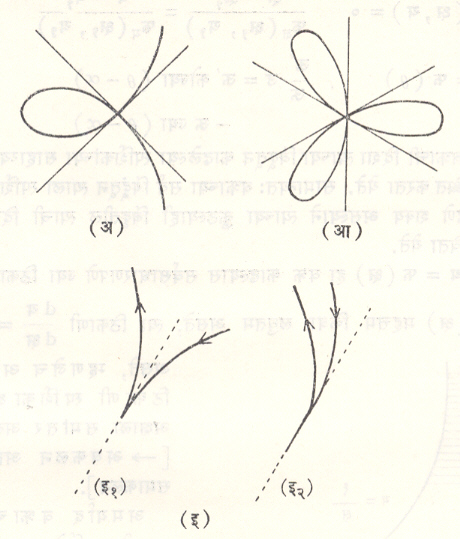
वक्रावरील असाधारण बिंदू : वक्रावरील बिंदूंचे वर्गीकरण त्यांच्या ठायी वक्रास काढता येणाऱ्या स्पर्शिकांच्या संख्यांवरून करतात. एकच स्पर्शिका असल्यास त्या बिंदूस साधारण बिंदू व एकाहून अधिक स्पर्शिका असल्यास त्या बिंदूंस असाधारण बिंदू असे म्हणतात. जर स्पर्शिकांची संख्या न असेल, तर या बिंदूतून काढलेली रेषा त्या वक्रास न बिंदूंत छेदील म्हणजेच त्या बिंदूतून वक्राच्या न शाखा जातात. न ही त्या बिंदूची बहुगुणता होय. दोन भिन्न शाखा असलेल्या बिंदूस द्विगुण किंवा ग्रंथी बिंदू म्हणतात. जेव्हा त्या बिंदूतील दोन स्पर्शिका एकरूप होतात. त्या वेळी त्या बिंदूस शृंगबिंदू म्हणतात. वक्राच्या दोन्ही शृंग शाखा बिंदूच्या दोन्ही बाजूंस असल्यास त्यास सूचिशृंग व एकाच बाजूस असल्यास त्यास चंचुशृंग म्हणतात. वक्राचे बैजिक समीकरण दिल्यास विश्लेषण पद्धतीने वक्रावरील बिंदूंचे वर्गीकरण करता येते आणि त्यासंबंधीच्या वैश्लेषिक अटी काढता येतात. वक्राचा भ्रमणबिंदू शृंगारबिंदूपर्यंत जाऊन परत मागे येत असल्याने त्यास वक्राचा स्थिर असाधारण बिंदू असेही म्हणतात.

वक्रावरील बिंदूंप्रमाणेच वक्राच्या स्पर्शिकांबाबत अशा असाधारण बाबी आढळून येतात. ज्या स्पर्शिकेचा स्पर्शबिंदू एकमेव व निश्चित नसतो, अशा स्पर्शिकेला असाधारण स्पर्शिका म्हणतात. द्विगुण बिंदूप्रमाणेच द्विगुण स्पर्शिका वक्राला दोन भिन्न व साधारण बिंदूंत स्पर्श करते.

कधी कधी वक्राचा आकार असा विवक्षित असतो की, त्यामुळे प्रथम वक्राच्या एका अंगास (डाव्या) वक्रास स्पर्शिणाऱ्या स्पर्शिका एका विशिष्ट बिंदूनंतर वक्राच्या विरुद्ध (उजव्या) अंगास त्याला स्पर्श करताना आढळतात. या बिंदूस नतिपरिवर्तन बिंदू म्हणतात (आ. ११). त्या बिंदूच्या ठायी वक्राची वक्रता शून्य असते. या बिंदूच्या दोन बाजूंस वक्राची अंतर्वक्रता विरुद्ध दिशेत असते.

काही वक्रांच्या बाबतीत त्यांचे काही बिंदू वक्राच्या इतर अंगापासून वेगळे असलेले आढळतात. या बिंदूस एकाकी बिंदू असे म्हणतात (आ. १२). या बिंदूतील वक्राची स्पर्शिका असत् असते.

समीकरणाच्या स्वरूपावरून वक्रांचे वर्गीकरण : वक्राचे समीकरण बैजिक स्वरूपाचे असल्यास त्यास बैजिक वक्र असे म्हणतात. इतर वक्रांस बीजातीत वक्र म्हणतात.

बैजिक वक्राच्या समीकरणावरून त्याचा घात ठरविला जातो. अकरणी (वर्गमूळ, घनमूळ वगैरे मूळदर्शक क्रिया नसलेल्या) स्वरूपात समीकरण मांडल्यानंतर त्यातील चलपदांच्या उच्चतम घात पूर्णांकास त्या समीकरणाचा किंवा त्याने निर्देशिलेल्या वक्राचा घात म्हणतात. त्यास वक्राचा क्रमांकही म्हणतात. न घातीय वक्राच्या समीकरणातील पदांची संख्या सामान्यतः (न+१) (न+२) /२ एवढी असते, तर स्वतंत्र स्थिरांकांची संख्या (न+१) (न+२)/२– १ = न(न+३)/२ एवढी असते. यामुळेच न घातीय वक्र न (न +३)/२ बिंदूंनी निश्चित होतो. कुठलीही सरळ रेषा वक्रास जास्तीत जास्त त्याच्या घातसंख्येएवढ्या बिंदूंत छेदू शकते.

वक्राच्या स्पर्शिका समीकरणाच्या घातांकास वक्राचा वर्ग क्रमांक असे म्हणतात. कुठल्याही बिंदूतून वक्रास जास्तीत जास्त या वर्गसंख्येइतक्याच स्पर्शिका काढता येतात. सामान्यतः वक्राचा वर्ग क्रमांक त्याच्या घाताहून भिन्न असतो.

न घातीय वक्राबाबत द्विगुण बिंदू व शृंगबिंदू यांची संख्या जास्तीत जास्त (न–१) (न–२)/२ असू शकते. द्विगुण बिंदू व शृंगबिंदू यांची प्रत्यक्ष संख्या द+श असल्यास त्यांची जास्तीत जास्त शक्य संख्या (न–१) (न–२)/२ आणि प्रत्यक्ष संख्या द+श यांच्यातील फरकास वक्राची न्यूनता असे म्हणतात.

एखाद्या वक्राबाबत असाधारण बिंदू अस्तित्वात नसल्यास, असाधारण स्पर्शिका जास्त संख्येने अस्तित्वात असतात. असाधारण बिंदू अस्तित्वात असल्यास या स्पर्शिकांची संख्या कमी असते. वक्राचा घात न, वर्ग क्रमांक व, द्विगुण बिंदूंची संख्या द, शृंगबिंदूंची संख्या श, द्विगुण स्पर्शिकांची संख्या स्प आणि नतिपरिवर्तन बिंदूंची संख्या प असल्यास या सर्वांचा परस्परसंबंध खालील समीकरणांनी दर्शविला जातो.

व = न (न–१)–२ द–३ श

प–श = ३ ( व–न )

२ (स्प–द) = ( व–न ) (व+न–९)

या समीकरणांचे प्रणेते जर्मन गणितज्ञ यूलिउस प्ल्यूकर (१८०१–६८) यांच्या नावावरून ‘प्ल्यूकर समीकरणे’ म्हणून ती ओळखली जातात.

वक्र ज्या प्रतलात आहे त्यातील कुठल्याही एका क बिंदूतून वक्राला काढलेल्या असाधारण स्पर्शिकांचे स्पर्शबिंदू एक वक्र निर्माण करतात. हा वक्र मूळ वक्राच्या बहुगुण बिंदूतूनही जातो. याप्रमाणे मूळ वक्र व हा निर्माण झालेला वक्र हे परस्परांस मूळ वक्राचे असाधारण बिंदू आणि असाधारण स्पर्शिकांचे स्पर्शबिंदू या बिंदूंत छेदतात. या वक्रास क बिंदूचा मूळ वक्राच्या संदर्भातील प्रथम ध्रुवीय वक्र म्हणतात. प्रथम ध्रुवीय वक्र मूळ वक्रास त्याच्या द्विगुण बिंदूत दोन एकत्रित बिंदूंत छेदतो, तर त्याच्या शृंगबिंदूत त्याला त्याच्या तीन एकत्रित बिंदूंत स्पर्श करतो. ध्रुवीय वक्राचा घात (न–१) असून प्ल्यूकर यांच्या पहिल्या समीकरणावरून प्रथम ध्रुवीय वक्र व मूळ वक्र यांच्या छेदनबिंदूंची संख्या न (न–१) असल्याचे स्पष्ट होते.

दोन वक्र परस्परांस ज्या बिंदूत छेदतात त्या बिंदूंचे सहनिर्देशक दोन्ही वक्रांच्या समीकरणांची पूर्ती करतात. या बिंदूंची संख्या (एका वक्राचा घात × दुसऱ्या वक्राचा घात) एवढी असते. यातच अनंत अंतरावरील छेदनबिंदूचाही समावेश असतो.

वक्राच्या समीकरणाची उजवी बाजू शून्य राहील अशा प्रकारे मांडणी केल्यास, कधीकधी डाव्या बाजूच्या राशीचे पृथक्करण करून अवयव पाडता येतात. यांपैकी कुठलाही एक अवयव = ० घेतल्यास एक स्वतंत्र वक्र मिळतो. प्रत्येक अवयवास एक वक्र याप्रमाणे वक्राचा एक समूह येथे निर्माण होतो. या समूहातील प्रत्येक वक्रावरील बिंदूंचे सहनिर्देशक मूळ वक्राच्या समीकरणाची पूर्ती करतात. याप्रमाणे मिळणाऱ्या वक्रसमूहाचा अपकृष्ट वक्र असाही निर्देश करता येतो. या समूहातील सर्व वक्रांच्या घातांच्या बेरजेस त्या समूहाने निर्देशिलेल्या अपकृष्ट वक्राचा घात असे म्हणतात. याप्रमाणे एक ⇨शंकुच्छेद व त्याला दोन बिंदूंत छेदणारी त्याच प्रतलातील एक सरळ रेषा या दोन्हींचा एक त्रिघातीय अपकृष्ट वक्र असा निर्देश करता येतो.

अवकाश वक्राबाबत असे पृथक्करण नेहमीच शक्य होते असे नाही. एक शंकुच्छेद व त्याच प्रतलात नसलेली पण त्याला एका बिंदूत छेदून जाणारी सरळ रेषा यांचा एक अवकाश अपकृष्ट वक्र असा निर्देश करता येतो. मात्र ही रेषा त्या शंकुच्छेदाला प्रत्यक्ष न छेदता त्याच्या प्रतलात दुसऱ्या बिंदूत छेदून गेल्यास हे शक्य होत नाही.

कुठल्याही एका वक्रावरील प्रत्येक बिंदूस अनुलक्षून दुसऱ्या वक्रावरील एकमेव व निश्चित बिंदू मिळविता आल्यास दुसऱ्या वक्रास पहिल्या वक्राचा रूपांतरित वक्र असे म्हणतात. येथे पहिल्या वक्राच्या प्रत्येक बिंदूपासून दुसऱ्या वक्रावरील एकच बिंदू मिळत असल्याने ह्या बिंदूच्या सहनिर्देशकांचा संबंध एकमूल्यी फलनाने व्यक्त करता येतो. रूपांतरित वक्राची न्यूनता मूळ वक्राएवढीच असते. प्रतल वक्र व अवकाश वक्र या दोन्ही प्रकारांच्या वक्रांबाबत रूपांतरण शक्य होते.

वक्राचे अनुरेखन: वक्राच्या समीकरणावरून त्याची आकृती तयार करणे यासच वक्राचे अनुरेखन असे म्हणतात. यासाठी वक्राच्या समीकरणांचा अभ्यास खालीलप्रमाणे केला जातो.

(१) सममिती : वक्राचे स्वरूप ठरविण्यासाठी प्रथमतः त्याची सममिती जाणून घ्यावी. वक्राबाबत कधीकधी एखादी रेषा अशी आढळते की, ज्या रेषेतून वक्रास घडी घातल्यास रेषेच्या एका बाजूकडील वक्राचा प्रत्येक बिंदू दुसऱ्या बाजूकडील वक्राच्या एका बिंदूशी संलग्न होतो. या रेषेस त्या वक्राचा सममिती अक्ष असे म्हणतात. (आ. १३).

त्याचप्रमाणे वक्रावर असा एक बिंदू आढळतो की, त्यातून जाणारी वक्राची कोणतीही जीवा त्या बिंदूच्या ठायी दुभागली जाते. अशा बिंदूस वक्राचा सममिती बिंदू असे म्हणतात. (आ. १४). सममिती रेषा व बिंदू खालीलप्रमाणे ठरविता येतात.

(अ) य = ० योजून, क्ष ऐवजी–क्ष ठेवून समीकरणात फरक न झाल्यास सममितीची रेषा क्ष = 0 (य अक्ष) असते.

(आ) क्ष = ० ठेवून य ऐवजी–य ठेवून समीकरण आहे तसेच राहिल्यास य = ० (क्ष अक्ष) ही सममिती रेषा असते.

(इ) अ आणि आ हे दोन्ही योजून समीकरण तसेच राहिल्यास वक्र (०,० ) म्हणजेच आदिबिंदूसापेक्ष सममित असतो.

याप्रमाणे इतर कोणत्याही बिंदूच्या सापेक्ष सममिती शोधण्याकरिता त्या बिंदूत आदिबिंदूचे स्थलांतरण करून वरीलप्रमाणे क्रिया केली जाते.

(ई) य ऐवजी क्ष ठेवून समीकरण आहे तसेच राहिल्यास सममिती रेषा क्ष = य असते. क्ष आणि य अक्षांच्या सापेक्ष सममिती आणखी एका पद्धतीने ठरविता येते. समीकरणातील य चे घातांक सम असल्यास वक्र क्ष अक्षसापेक्ष सममित असतो, तर याउलट क्ष चे घातांक सम असल्यास तो य अक्षसापेक्ष सममिती असतो. दोन्हींचे घातांक सम असल्यास तो दोन्ही अक्षांच्या सापेक्ष सममित असतो.

(२) अंतर्च्छेद : वक्र अक्षाचा जो भाग कापून जातो त्या भागास (वक्राचा अक्षावरील छेदनबिंदू व आदिबिंदू यांतील अंतरास) वक्राचा त्या अक्षावरील अंतर्च्छेद म्हणतात. वक्राच्या समीकरणात य = ० किंवा क्ष = ० ठेवून वक्राचे अनुक्रमे क्ष आणि य अक्षावर छेदणारे बिंदू मिळतात.

कधीकधी वक्राच्या समीकरणावरून तो वक्र ज्या मर्यादित क्षेत्रात समविष्ट असतो ते क्षेत्र ठरविता येते.

वक्र समीकरणाच्या अभ्यासातली पुढची पायरी म्हणजे तो वक्र आदिबिंदूतून जातो किंवा नाही हे पाहणे ही होय. त्यासाठी क्ष = य = ० ठेवून समीकरणाची पूर्ती होते की नाही ते पाहिले जाते.

वक्र आदिबिंदूतून जात असल्यास आदिबिंदूतून वक्राच्या स्पर्शिका मिळविल्या जातात. त्यासाठी वक्र समीकरणातील सर्वांत कमी घातांची पदे असलेली राशी = ० मांडण्यात येते. यावरून स्पर्शिकांची समीकरणे निश्चित होतात. या स्पर्शिकांमुळे वक्राचे आदिबिंदूनजीकचे स्वरूप स्पष्ट होते.

वक्राच्या अनंतस्पर्शिका त्याचे स्वरूप निश्चित करण्यास मदत करतात. अक्षास समांतर असलेल्या अनंतस्पर्शिका पुढीलप्रमाणे मिळवितात. क्ष च्या उच्च घातीय पदांची सहगुणक राशी = ० धरल्यास क्ष अक्षाला समांतर असलेल्या अनंतस्पर्शिका, तर य च्या उच्च घातीय पदांची सहगुणक राशी = ० धरल्यास य अक्षाला समांतर असलेल्या अनंतस्पर्शिका निश्चित होतात.

इतर अनंतस्पर्शिका मिळविण्यासाठी स्टर्लिंग यांच्या पद्धतीचा उपयोग करता येतो. या पद्धतीनुसार वक्र समीकरणाची य=अ क्ष+क+ख/क्ष+ग/क्ष²+….. अशी मांडणी केल्यास य=अक्ष+क हे अनंतस्पर्शिकेचे समीकरण मिळते. यातील ख या स्थिरांकाचे चिन्ह + असल्यास वक्र अनंतस्पर्शिकेस स्पर्श करण्याकरिता वरून खाली येतो, तर ख चे चिन्ह – असल्यास तो खालून वर येतो. यावरून वक्र अनंतस्पर्शिकेच्या कोणत्या अंगाला आहे हेही निश्चित होते. कधीकधी वक्राच्या समीकरणावरून निरीक्षणानेही अनंतस्पर्शिका ठरविता येते.

वक्राच्या अनुरेखनाकरिता वक्रावरील विशेष बिंदू निश्चित करणे आवश्यक असते. आदिबिंदू हा असाधारण बिंदू आहे की नाही ते पाहिले जाते.

वक्रावरील महत्तम व लघुत्तम बिंदू ठरविल्यास वक्राचे उंचवटे व खळगे कळू शकतात.

वक्राचे समीकरण य = फ (क्ष) या स्वरूपात मांडून क्ष च्या निरनिराळ्या मूल्यांनुसार य च्या मूल्यांत होणारा बदल लक्षात घेतला जातो. वक्राचा आकार व त्याची वेटोळी ठरविण्यास यामुळे मदत होते.

कधीकधी वक्राच्या समीकरणाचे ध्रुवीय पद्धतीत रूपांतर केल्यास त्याचे अनुरेखन अधिक सुलभ होते. वक्राच्या ध्रुवीय समीकरणात θ ऐवजी –θ ठेवून समीकरण आहे तसेच राहिले, तर वक्र स्थिर रेषासापेक्ष सममित असतो, तर समीकरणातील र चे घातांक सम असल्यास वक्र ध्रुवबिंदूसापेक्ष सममित असतो.

वक्राचे समीकरण र = फ (θ) या स्वरूपात मांडून θ ला निरनिराळी मूल्ये देऊन त्यानुसार होणारा र च्या मूल्यातील बदल लक्षात घेतला जातो. यात θ = ० व θ = ∞ ही मूल्ये योजून त्या ठिकाणी र ची मूल्ये मिळविली जातात.

स्प ø = र dθ/ dर हे मूल्य काढून वक्राच्या स्पर्शिकेची दिशा निश्चित करता येते.

वक्राच्या अनंतस्पर्शिका मिळविण्यासाठी θ च्या ज्या मूल्यास र =∞ होईल ती मूल्ये शोधली जातात.

वक्राबाबत अनंतस्पर्शिका वर्तुळ अस्तित्वात आहे की काय ते पाहिले जाते. वक्राचे नतिपरिवर्तन बिंदू उ=d²उ/dθ² =०, (उ =१/र) यावरून मिळविता येतात.

वक्राचे अन्वायोजना : प्रयोगातील निरीक्षणांची मांडणी समीकरणरूपात केल्यास प्रयोगाची फलश्रुती अधिक स्पष्ट होते. याकरिता या निरीक्षणांना बिंदूंचे सहनिर्देशक कल्पून या बिंदूंतून जाणारा वक्र मिळविला जातो. निरीक्षणांना वक्रावरील बिंदूंचे सहनिर्देशक कल्पिल्यामुळे ही निरीक्षणे या वक्राच्या समीकरणाची पूर्ती करतात. म्हणजेच हे समीकरण वरील निरीक्षणांची फलश्रुती दाखविते. या क्रियेस वक्राचे अन्वायोजन म्हणतात. यासंबंधीची अधिक माहिती ‘अंतर्वेशन व बहिर्वेशन’ आणि ‘आलेख’ या नोंदींत दिलेली आहे.

काही महत्त्वाचे प्रतल वक्र : वैश्लेषिक भूमितीच्या अभ्यासातून बऱ्याच वैशिष्ट्यपूर्ण वक्रांची निर्मिती झाली. त्यांतील काही वक्र खालीलप्रमाणे आहेत. याचे सामान्य स्वरूपातील समीकरण य = अक्ष^३ + कक्ष^२ + खक्ष+ग असे असते. या वक्राचा अभ्यास न्यूटन यांनी केला. यातलाच एक विशिष्ट प्रकार य=अक्ष^३ मात्र प्रथम जी. डब्ल्यू. लायप्निट्स यांनी अभ्यासला. त्यांनीच या प्रकाराबाबत अवप्रलंब हा य सहनिर्देशकावर व्यस्त प्रमाणात अवलंबून असल्याचे सिद्ध केले. गास्पार माँझ यांनी या वक्राच्या साहाय्याने क्ष^३–पक्ष+फ=० या समीकरणाचा निर्वाह मिळविण्याचा प्रयत्न केला.

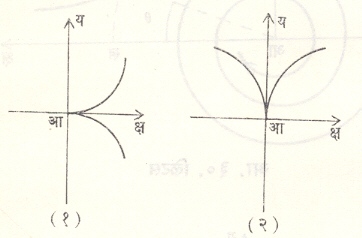
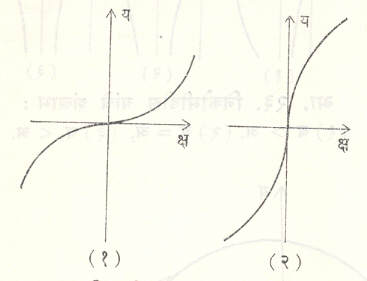
त्रिघातीय अन्वस्त : य = अ क्ष^३ हा त्रिघातीय अन्वस्त आदिबिंदूतून जात असून त्या बिंदूच्या ठायी वक्राचा नतिपरिवर्तन बिंदू असतो. त्रिघातीय अन्वस्ताचे समीकरण य=अक्ष^३ असल्यास वक्र क्ष अक्षाला व ते क्ष=अय^३ असल्यास य अक्षाला स्पर्श करतो. (आ. १५).

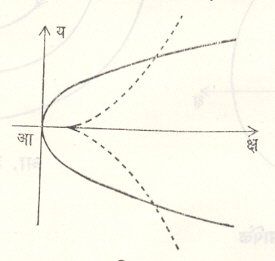
अर्धत्रिघातीय अन्वस्त : याचा अभ्यास नील १६५९ साली केला. याचे समीकरण क्ष^३ = अ य^२ असे किंवा य^३ = अ क्ष^२ असे मांडल्यास याचा शृंगबिंदू आदिबिंदूच्या ठायी असतो. पहिल्या प्रकारात क्ष–अक्ष, तर दुसऱ्यात य–अक्ष वक्रास स्पर्श करतो (आ. १६). हा वक्र अन्वस्ताचा उद्वलित होय. अन्वस्ताचे समीकरण य^२ = ४ अ क्ष घेतल्यास याचे समीकरण २७ अ य^२ = ४ (क्ष – २ अ)^३ असते. उद्वलिताच्या (आ. १७) उजव्या बाजूकडील बिंदूंतून अन्वस्तास ४ निश्चित प्रलंब काढता येतात, तर डाव्या बाजूकडील बिंदूंतून फक्त एकच निश्चित प्रलंब काढता येतो. क्रिस्तीआन हायगेन्झ यांनी गुरुत्वाकर्षण क्षेत्रात पदार्थ कणाला सारख्या वेळात उभे समान अंतर कापील अशा रीतीने खाली येऊ दिल्यास, तो वरील वक्राच्या स्वरूपातील मार्गानेच खाली येतो, हे सिद्ध केले.

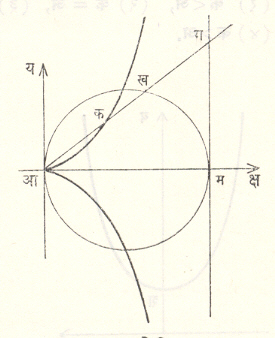
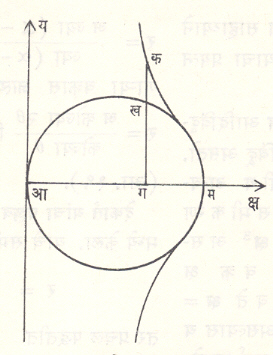
डायोक्लिज यांचा सिसॉइड : (शिंजीनी वक्र). डायोक्लिज (इ. स. पू. सु. १००) या ग्रीक गणितज्ञांनी या वक्राचा शोध लावला. याचे समीकरण कार्तीय पद्धतीत य^२ (२ अ – क्ष) = क्ष^३ असे, तर ध्रुवीय पद्धतीत र = २ अ स्प θ ^.ज्या θ असे असते. आदिबिंदू हा या वक्राचा शृंगबिंदू आहे, तर क्ष = २ अ ही अनंतस्पर्शिका आहे. या वक्राबाबत आ क = ख ग असते, तर वक्र व अनंतस्पर्शिका यांनी अंतर्भूत केलेले क्षेत्र आम ला व्यास कल्पून काढलेल्या वर्तुळाच्या क्षेत्राच्या तिप्पट असते. (आ. १८).

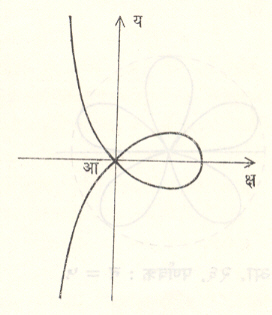
स्ट्रोफॉइड : (कुंचित वक्र). याची प्रथम निर्मिती आयझॅक बॅरो यांनी १६७० साली केली. याचे सामान्य स्वरूपातील समीकरण र = अ ज्या (∝−२θ) / ज्या (∝−θ) असते. यांत ∝ = ९०^° असल्यास मिळणाऱ्या वक्रास जात्य स्ट्रोफॉइड म्हणतात. या वेळी समीकरण र = अ कोज्या २θ/कोज्या θ किंवा य^२ (अ–क्ष) = क्ष^२(अ+क्ष) असते. (आ. १९).

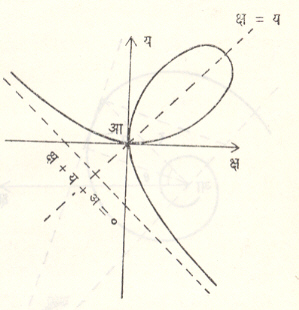
देकार्त यांचा पल्लव वक्र : ह्या वक्राचा अभ्यास देकार्त यांनी १६३८ मध्ये केला. याचे समीकरण ध्रुवीय पद्धतीत र = ३ अ ज्या θ ^. कोज्या θ/ कोज्या^३θ + ज्या^३ θ तर प्रचल पद्धतीत क्ष = ३ अ ट/१+ट^३ ; य = ३ अ ट^२/१ ट^३ असते.

याचे अनुरेखन ध्रुवीय पद्धतीने सोपे होते. कार्तीय पद्धतीत याचे समीकरण क्ष^३+ य^३ = ३ अ क्ष य असे असून अनंतस्पर्शिका क्ष+य+अ = ० ही असते. (आ. २०)

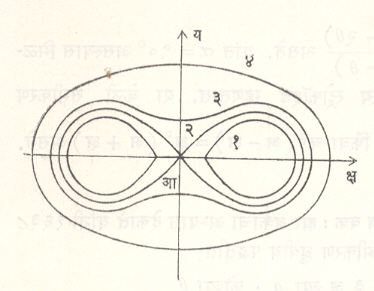
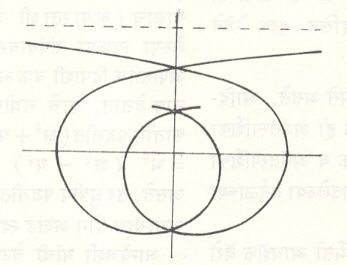
कासीनी यांचे अंडाकृती वक्र : यांची निर्मिती जे. डी. कासीनी यांनी १६८० साली केली. दोन स्थिर बिंदूंपासूनच्या अंतराचा गुणाकार स्थिरांक राहील अशा रीतीने फिरणाऱ्या बिंदूंचा बिंदुपथ अशी याची व्याख्या करतात. हा स्थिरांक = क^२ मानल्यास वक्राचे समीकरण (क्ष^२+य^२)–२अ^२(क्ष^२–य^२)+अ^४–क^४= ० असते. येथे क < अ असल्यास वक्र दोन स्वतंत्र वेटोळ्यांच्या स्वरूपात मिळतो. क=अ असल्यास मिळणाऱ्या वक्रास याकोप (झाक) बेर्नुली (१६९४) यांचा द्विपाशी वक्र (लेम्निस्केट) असे म्हणतात. यालाच (अपास्ताशी असलेल्या त्याच्या संबंधावरून) अपास्तीय द्विपाशी वक्र असेही नाव देतात. याचे समीकरण कार्तीय पद्धतीत (क्ष^२+य^२)^२=अ^२(क्ष^२–य^२) असे असते, तर ध्रुवीय पद्धतीत र^२=अ^२ कोज्या २ θ असे असते. क > अ असल्यास दोन अखंड स्वरूपातील वक्र प्रकार मिळतात. (आ.२१).

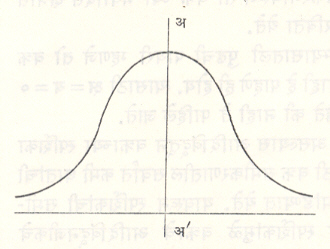
आन्येअझी यांची चेटकीण किंवा व्हर्सिएरा : मारिआ आन्येअझी या इटालियन स्त्री गणितज्ञांनी १७४८ मध्ये या वक्राचा अभ्यास केला. त्यापूर्वी प्लेअर द फेर्मा व ग्विदो ग्रांदी यांच्या लेखनांतही तो आढळतो (१७०३). याचे समीकरण य = अ^३ ⁄ (क्ष^२+अ^२) किंवा य = अ^२ (२अ–क्ष)/क्ष^२ असे असते. या वक्राची अनंतस्पर्शिका आणि वक्र यांमधील क्षेत्र हे आम ला व्यास कल्पून काढलेल्या वर्तुळाच्या क्षेत्राच्या चौपट असते आणि गख/गक = आग / आम असते. (आ.२२).

---

---

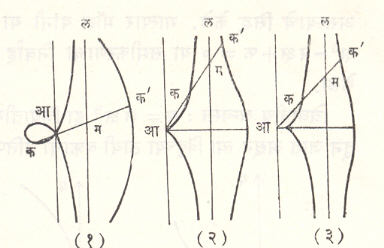
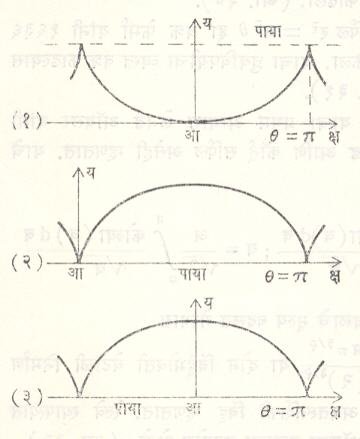
निकोमीडीझ यांचे शंखाभ : (कॉन्कॉइड). आ या स्थिर बिंदूपासून अचल (अ) अंतरावर ल ही रेषा घ्या. आ बिंदूतून काढलेली कोणतीही रेषा ल रेषेला म बिंदूत छेदील. आम रेषेवर क व क’ असे बिंदू घ्या की, मक=मक’=अचल ब. यातील क,क’ चे बिंदुपथ म्हणून जे वक्र मिळतात त्यास निकोमीडीझ (इ. स. पू. सु. २४०) यांचे शंखाभ म्हणतात. अ ब घेतल्यास तीन प्रकारचे वक्र मिळतात.ते आ. २३ मध्ये दाखविले आहेत.

घनाचे दुप्पटीकरण किंवा कोनाचे तीन भाग करणे यांकरिता या वक्राचा उपयोग करतात. हा वक्र यांत्रिक रीतीने मिळविता येतो.

रज्जुवक : एखादी पूर्णपणे लवचिक, एकविध रज्जू मुक्त स्वरूपात टांगली असता ती ज्या वक्रस्वरूपात स्थिर होते त्या वक्रास रज्जुवक्र असे म्हणतात. (आ.२४). १६९१ साली हायगेन्झ व लायप्निट्स यांनी या वक्राचे समीकरण य = अ/२(e ^{क्ष/अ}+ e^{–क्ष/अ}) अ अपाकोज्या (क्ष/अ) असे मिळविले. श बंदूस या वक्राचा शिरोबिंदू, क्ष अक्षास नियतरेषा, तर य अक्षास त्याचा अक्ष असे म्हणतात. हा वक्र क्ष अक्षाभोवती फिरविला असता निर्माण होणाऱ्या पृष्ठास रज्जुवक्रज म्हणतात. अन्वस्त एका सरळ रेषेवर फिरविला असता त्याच्या केंद्रबिंदूने निर्मिलेला पथ म्हणजेच अन्वस्ताच्या नाभिबिंदूचा परिवलन (वेल्लज) काढल्यास रज्जुवक्रमिळतो.त्यावरूनच रज्जुवक्रास अन्वस्तीय रज्जुवक्र म्हणतात. त्याप्रमाणेच विवृत्तीय (दीर्घवृत्तीय) रज्जुवक्र व अपास्तीय रज्जुवक्र ही नावे दिली जातात.

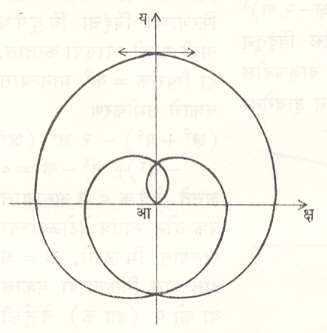
पास्काल यांचे लिमॅकॉन : एत्येन पास्काल (ब्लेझपास्काल यांचे वडील) यांनी शोधून केढलेल्या व जी. बी. रोबेरव्हाल यांनी नाव दिलेल्या (१६५०) या वक्राचे समीकरण (क्ष^२+य^२–२अक्ष)^२= ब^२ (क्ष^२+य^२) किंवा ध्रुवीय पद्धतीत र=ब+२अ कोज्या qअसते. यात ब &gt २अ, ब= २ अ आणि ब= अ या तीन मुल्यांनुसार मिळणारे तीन प्रकारचे वक्र आ. २५ मध्ये दाखविल्याप्रमाणे मिळतात. ब = अ असल्यास मिळणाऱ्या वक्रास कार्डिऑइड (हृदयाकृती वक्र) असे म्हणतात. याचे प्रचल स्वरूपातील समीकरण. क्ष = अ (२ कोज्या q–कोज्या२ q), य=अ (२ज्या q–ज्या २q) असते. याचा प्रथम अभ्यास जे. केर्स्मा यांनी केला.

पर्णवक्र : याचा आकार पानाच्या झुपक्यासारखा असल्याने यास पर्णवक्र असे म्हणतात. यात दोन प्रकार आढळतात :

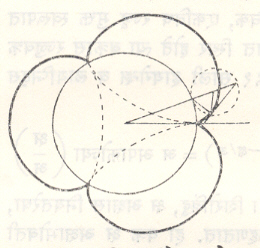
(१) र=अ कोज्या (न q), (२) र=अ ज्या (न q). यांपैकी र = अ ज्या (न q) यात न चे मूल्य विषम असल्यास न वेटोळी, तर म चे मूल्य सम असल्यास २ न वेटोळी मिळतात. ही सर्व वेटोळी अ त्रिज्या असलेल्या व ध्रुवबिंदू मध्य कल्पून काढलेल्या वर्तुळात समाविष्ट असतात. (आ.२६).

र^न= अ^न कोज्या (नq) हा महत्त्वाचा वक्र गट आहे. यात न ला विशिष्ट मूल्य देऊन काही परिचित वक्र मिळतात. जसे, न=२बेर्नुली यांचा द्विपाशी वक्र (लेग्निस्केट) न = १ वर्तुळ (परिघस्थ ध्रुवबिंदू) न=- १/२ अन्वस्त (नाभी ध्रुवबिंदू) न =–१ सरळ रेषा.

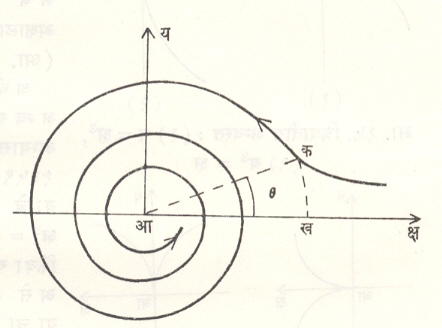
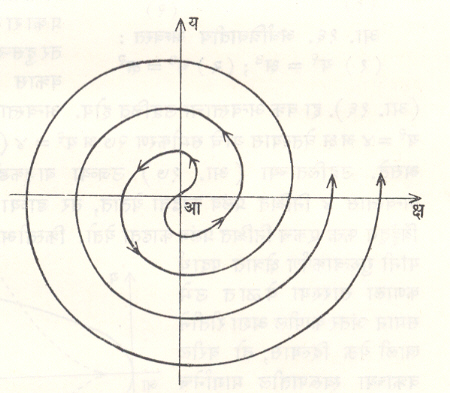
सर्पाकृती वक्र किंवा सर्पिल : काही वक्रांच्या बाबतीत त्यांच्या ध्रुवीय समीकरणातील [र= फ(q)] qचे मूल्य वाढवीत गेल्यास र चे मूल्य अखंडपणे एकतर वाढत जाते किंवा कमी होत जाते. या वेळी मिळणारा वक्र ध्रुवाभोवती वेटोळी निर्माण करतो व त्यास सर्पाकृती वक्र किंवा सर्पिल असे म्हणतात.

समकोनीय किंवा लॉगरिथमीय सर्पिल: याचे समीकरण र= अe ^{qकोस्पa}असे असते. या वक्राच्या कुठल्याही बिंदूतून वक्रास काढलेली स्पर्शिका त्या बिंदूतील त्रिज्या सदिशाशी aहा स्थिर कोन करते. (आ. २७).

आर्किमिडीज सर्पिल : याचे समीकरण र = अ qअसे असते. या वक्राबाबत ध्रुव मध्य कल्पून अ त्रिज्येचे वर्तुळ काढल्यास आदिरेषा व वक्रावरील कुठलाही एक बिंदू यांत कापली गेलेली वर्तुळाची कंस लांबी त्या बिंदूच्या त्रिज्या सदिशांच्या लांबीएवढी असते. याच्या अवप्रलंबाची लांबी नेहमी स्थिर असून ती अ असते. वर्तुळाच्या आवलिताचा त्याच्या मध्यबिंदूसंबंधात पदिक-वक्र (स्पर्शिकेला स्थिर बिंदूपासून काढलेल्या लंबाच्या पायाचा बिंदूपथ) काढल्यास हे सर्पिल मिळते. (आ. २८).

व्यस्त सर्पिल : र q = अ हा र=अ qयाचा व्यस्त वक्र होय. आदिरेषा व हा वक्र यांनी कापलेला, ध्रुवबिंदू मध्य कल्पून काढलेल्या कोणत्याही वर्तुळाचा चाप हा स्थिर लांबीचा असतो. याचा अभ्यास प्रथम प्येअर व्हॅरिग्नॉन यांनी १७०४ मध्ये केला. (आ.२९).

लिटस :याचे समीकरण र√q= अ असते. या वक्रावरील कुठल्याही बिंदूतील त्रिज्या सदिशालात्रिज्या व ध्रुवाला मध्य कल्पुन काढलेल्या वर्तुळाचे, त्रिज्या सदिश व स्थिर रेषा यांनी मर्यादित केलेले क्षेत्रफळ (आकख) स्थिर असते. रॉजर कोट्स यांनी हा वक्र १७२२ साली शोधून काढला. (आ.३०).

फेर्मा सर्पिल :सर्पिल र^२ = अ^२ qहा वक्र फेर्मा यांनी १६३६ साली प्रथम निर्माण केला. याचा ध्रुवविषयीचा व्यस्त वक्र काढल्यास लिटस मिळतो. (आ.३१).

ऑयलर सर्पिल :याचा प्रथम अभ्यास लेनर्ड ऑयलर यांनी केला. याला क्लॉथॉइड आणि कॉर्नू सर्पिल असेही म्हणतात. याचे समीकरण

क्ष=अ/√2 _०ò ^वज्या(व)dव/√व य=अ/√2 _०ò ^वकोज्या(व)d व / अ/√व

असे असते व या प्रचालाचे मूल्य बदलत गेल्यास

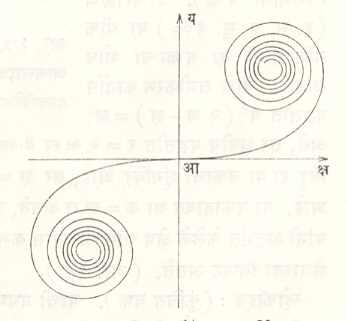
±अπ^१/२/(२)^३/२, ±अπ^१/२/(२)^३/२या दोन बिंदूंभोवती वेटोळी निर्माण होतात. या बिंदूस अनंतस्पर्शिकी बिंदू म्हणतात. रेल्वे स्थापत्यात संक्रमण वक्र म्हणून ऑयलर वक्राचा उपयोग होतो. (आ.३२).

---

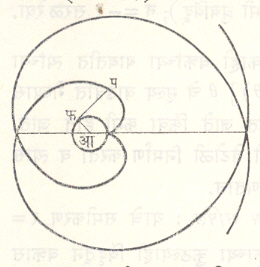
वर्तुळाचा आवलित : एक सरळ रेषा एका वर्तुळाला स्पर्श करीत राहील अशा रीतीने फिरविली असता तिच्यावरील कुठल्याही एका बिंदूने या भ्रमणातून निर्माण केलेला वक्र म्हणजेच त्या वर्तुळाचा आवलित होय. ही सरळ रेषा मूळ वक्राची स्पर्शिका असते, तर आवलिताची ती प्रलंब असते. या आवलिताचे पदिक समीकरण र^२=f^२अ^२, तर प्रचलात्मक समीकरण  क्ष = अ (कोज्याf+ fज्याf), य = अ (ज्याf-कोज्याf) असते. (आ. ३३).

मालाचलित: (ट्रॅक्ट्रिक्स किंवा समस्पर्शी वक्र). याचे समीकरण

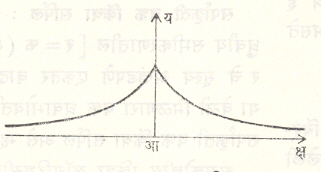
क्ष=अ[कोज्या व+लॉग स्पर्श (व/२)], य=अ ज्या (व) असते, याचा अभ्यास हायगेन्झ (१६९२), लायप्निट्स, योहान बेर्नुली वगैरेंनी केला. ज्यांचे मध्य क्ष अक्षावर आहेत व ज्यांची त्रिज्या–अ आहे अशा वर्तुळांचा जात्य संच्छेदी (सर्व घटक वर्तुळांना काटकोनात छेदणारा वक्र) काढल्यास हा वक्र मिळतो. या वक्राचा उद्वलित रज्जवक्र स्वरूपात मिळतो. (आ. ३४)

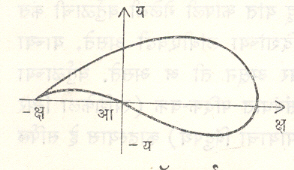
झुकॉव्हस्कई वक्र: (वातपर्ण). याचे समीकरण

क्ष = व+ व/व^२+व_१^२ य=व_१– व_१/व^२+व_१^२

येथे व आणि व_१ हे प्रचल व^२+व_१^२= २ह (व+व_१+१)+ १

या नियमाची पूर्ती करतात. सदसत् फलनांच्या [⟶फलन] अभ्यासात व’=झ+१/झ या रूपांतरणाने (–१) मधून जाणाऱ्या वर्तुळाच्या रूपांतरणानंतर हा वक्र मिळतो. ⇨वायुयामिकीत या वक्राला फार महत्त्व असून वायुयानांच्या अभिकल्पात (आराखड्यात) या वक्राचा उपयोग होतो. (आ. ३५).

परिवलज किंवा बेल्लज: (राउलेट). एक वक्र दुसऱ्या स्थिर वक्रावर फिरविला असता पहिल्या वक्रावरील कुठल्याहीएका बिंदूने निर्माण केलेल्या वक्रास परिवलज वा वेल्लज असे म्हणतात. उदा., एका अन्वस्त दुसऱ्या अन्वस्तावर फिरवला असता पहिल्याचा शिरोबिंदू डायोक्लिज वक्र तयार करतो, हाच परिवलज होय. चक्रजहाही एक परिवलज होय. वर्तुळ एका सरळ रेषेवर फिरवीत नेल्यास त्याच्या परिघावरील एखादा बिंदू प जो वक्र निर्माण करतो त्यास चक्रज म्हणतात. या सरळ रेषेस चक्रजाचा पाया असे म्हणतात. याचे अंगभूत समीकरण स=४ अ ज्या ψअसते. येथे अ ही फिरणाऱ्या वर्तुळाची त्रिज्या आहे. हा सर्वांत विख्यात वक्रांपैकी एक असून त्याचा अभ्यास गॅलिलिओ यांनी सु. १५९९ मध्ये केला व त्यास सायक्लॉइड (चक्रज) हे नाव दिले. त्यानंतर रोबेर्व्हाल (१६३४), सर क्रिस्टोफर रेन (१६५८), हायगेन्झ (१६७३), योहान बेर्नुली (१६९६) व इतरांनी त्याचा अभ्यास केला. याची प्रतल स्वरूपातील समीकरणे आदिबिंदू व अक्ष यांच्या निवडीनुसार खालील प्रकारात मिळतात.

(१) क्ष = अ (q + ज्या q), य = अ (१–कोज्या q) (२) क्ष = अ (q – ज्या q), य = अ (१ –कोज्या q) (३) क्ष = अ (q+ ज्या q) य = अ (१ + कोज्या q). प बिंदू वर्तुळाच्या परिघावर नसून वर्तुळमध्यापासून क अंतरावर असल्यास चक्रजाचे समीकरण खालीलप्रमाणे मिळते.

क्ष = अ q + क ज्या q,

य = अ –क कोज्या q

आहे. अंतश्चक्रज स्थिर वर्तुळाच्या आत तुटक रेषेने दाखविला आहे.

वरील सर्व चक्रज वक्र वर्तुळाच्या एका सरळ रेषेवरील भ्रमणाने तयार झाले आहेत. त्याएवजी वर्तुळ दुसऱ्या एका वर्तुळावर बाहेरील बाजूने फिरवल्यास फिरणाऱ्या वर्तुळाच्या परिघावरील एखाद्या बिंदूने निर्माण होणारा वक्र बहिश्चक्रज या नावाने ओळखला जातो. फिरविण्याची ही क्रिया दुसऱ्या वर्तुळाच्या आतील बाजूने केल्यास वक्रास अंतश्चक्रज म्हणतात. येथे दुसऱ्या वर्तुळाची त्रिज्या क असल्यास बहिश्चक्रजाचे समीकरण

क्ष=(अ + क) कोज्या q–क कोज्या (अ + क / क) q,

य = (अ + क) ज्या q–क ज्या (अ + क / क) q

तर अंतश्चक्रजाचे समीकरण

क्ष = (अ – क) कोज्या q + क कोज्या (अ –क / क) q

य = (अ – क) ज्या q–क ज्या (अ – क / क) q

असे असते. (आ. ३७).

क= अ/४ असल्यास चतुःशृंगी (चार शृंगे असलेला) अंतश्चक्रज मिळतो. याचे समीकरण क्ष=अ कोज्या^३ q, य=अ ज्या^३ qअशा स्वरूपात मांडता येते. येथे कार्तीय पद्धतीत ते

क्ष^२/३ + य^२/३ = अ^२/३ असे मिळते. (आ. ३८)

---

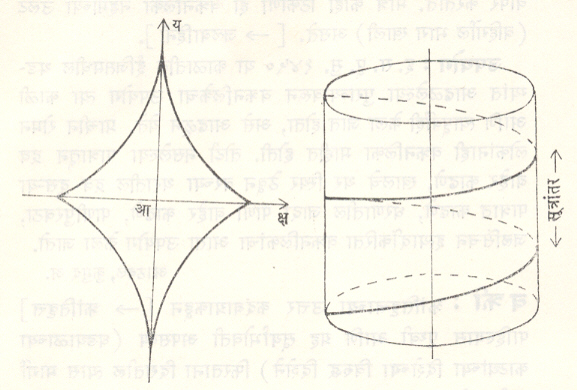काही महत्त्वाचे अवकाश वक्र:मळसूत्र: (आ. ३९). एका कागदावर त्याच्या खालच्या कडेस कोन (=q) करून काढलेली रेषा, तो कागद एका वर्तुळाकार चित्तीभोवती गुंडाळल्यास जो वक्र निर्माण करते त्यास मळसूत्र असे म्हणतात. येथे प्रत्येक परिभ्रमणात वक्र ज्या अंतराने वर जातो त्यास (दोन वेटोळ्यांमधील अंतरास) सूत्रांतर असे म्हणतात. याचे समीकरण

क्ष = र कोज्याq य=र ज्या q झ=ब q

असते. येथे ब हा स्थिरांक असून सूत्रांतर २ πब असते. चितीच्या जनक रेषेशी वक्राने केलेला कोन βअसल्यास ब=अ कोस्प βअसतो.

एकदिश नौपथ: (लोक्झोड्रोम). गोलाच्या याग्योत्तराशी (ध्रुव बिंदूतून जाणाऱ्या बृहत्वृत्ताशी) स्थिर कोन करित त्याला छेदणाऱ्या वक्रास एकदिश नौपथ असे म्हणतात. गोलाच्या दोन्ही ध्रुवबिंदूभोवती हा वक्र वेटोळे निर्माण करतो म्हणजेच ते बिंदू वक्राने अनंतस्पर्शी बिंदू असतात. याचा प्रथम अभ्यास पेद्रू नूनिश या पोर्तुगीज गणितज्ञांनी १५३४–३७ या काळात केला. याम्योत्तराशी केलेला स्थिर कोन β, वक्रावरील कुठल्याही एका बिंदूस रेखांशदर्शक fव अक्षांशदर्शक qअसल्यास वक्राचे समीकरण

क्ष = ज्या f.कोज्या q य = ज्या f. ज्या qज्या q झ = कोज्या qअसे असते. येथे q=-स्प βलॉग स्प (f/२) असतो. एकदिश नौपथ हाच गोलावरील दोन बिंदूतील किमान अंतर असल्याने पाणबुड्यांच्या मार्गनिर्दशनासाठी याच वक्र स्वरूपातील मार्गाचा अवलंब करतात.

अनेक विज्ञान शाखांत, विशेषतः अभियांत्रिकीत, वक्रांचा अभ्यास उपयुक्त ठरतो.

पहा: अन्वस्त अवास्त आलेख त्रिकोणमिती फलन भूमिती वर्तुळ विवृत्त शंकुच्छेद.

संदर्भ: 1. Coolidge, J. L. A Treatise on Algebraic Plane Curves London, 1959.

2. Edwards, J. An Elementary Treatise on the Differential of Calculus, London, 1961.

3. Johnson, D. A. Curves in Space, New York, 1963.

4. Morrill, W. K. Analytic Geometry, Scranton, 1964.

5. Walker, R. J. Algebraic Curves, Princeton, 1955.

6. Wartikar, P. N. Wartikar, J. N. Elements of Applied Mathematics, Poona, 1965.

7. Yates, R. C. Handbook of Curves and their Properties, Baltimore, 1959.

8. Zwikker, C. Advanced Geometry of Plane Curves and their Applications, New York, 1963.

काळीकर, मो. वि.

“