भिंग

भिंग : एक किंवा दोन वक्रपृष्ठांमध्ये अंतरित केलेल्या पारदर्शक माध्यमाच्या खंडाला भिंग असे म्हणतात. चष्मे, दूरदर्शक (दुर्बिणी), सूक्ष्मदर्शक, कॅमेरे इ. विविध प्रकारच्या प्रकाशीय उपकरणांमध्ये भिंगाचा उपयोग केला जातो. त्यामुळे त्यांच्या अभ्यासाला विशेष महत्त्व प्राप्त झालेले आहे.

इतिहास : काचेचा पोकळ गोल पारदर्शक द्रवाने भरल्यास त्यातून वस्तू (त्यांच्या प्रतिमा) मोठ्या झालेल्या दिसतात, ही गोष्ट प्राचीन ग्रीक व रोमन शास्त्रज्ञांना माहीत होती. इ. स. १५० मध्ये टॉलेमी (क्लॉडियस टॉलेमस) या प्रख्यात ग्रीक शास्त्रज्ञांनी आपल्या Optics या ग्रंथात अशा गोलांच्या काही गुणधर्मांचे वर्णन केले आहे. अकराव्या शतकातील अल्‍हॅझेन (इब्‍न अल हैथम) या अरब शास्त्रज्ञांनी आपल्या ग्रंथात या स्वरूपाच्या भिंगाबद्दल चर्चा केली आहे.

चष्म्यांच्या बहिर्गोल भिंगाबद्दल निःसंदिग्ध उल्लेख माईसनर यांनी तेराव्या शतकात केलेला आहे, तर अंतर्गोल भिंगाचा निर्देश नीकोलाऊस फोन कूझा यांनी पंधराव्या शतकाच्या मध्याला केला आहे. यानंतर भिंगाच्या साहाय्याने दूरदर्शक, सूक्ष्मदर्शक इ. उपकरणे तयार करता येतात हे शोध लागले. भिंगांबद्दल सैद्धांतिक व प्रायोगिक अभ्यास प्येअर द फेर्मा, सी. एफ्. गौस, जे. एल्. लाग्रांझ, आय्‍झॅक न्यूटन, एच्. एल्. एफ्. फोन हेल्महोल्ट्‍झ, अर्न्स्ट ॲबे इ. शास्त्रज्ञांनी केला.

आकार व वर्गीकरण : नेहमी वापरण्यात येणारी भिंगे सामान्य काचेची केलेली असतात. खास उपयोगासाठी क्वॉर्ट्‍झ, फ्ल्युओराइट किंवा प्लॅस्टिकाचीही भिंगे केल जातात. भिंगाची दोन्ही पृष्ठे वक्र किंवा एक वक्र व दुसरे समतल (सपाट) असते. वक्र पृष्ठे बहुधा गोलाचा एक भाग असतात. अशी पृष्ठे असणाऱ्या भिंगांना गोलीय भिंगे असे म्हणतात. खास उपयोगासाठी चित्याकार (दंडगोलाकार), विवृत्ताकार (लंबवर्तुळाकार) वगैरे आकाराची पृष्ठे असलेली अगोलीय भिंगेही केव्हा केव्हा वापरली जातात.

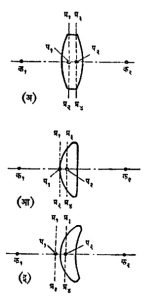
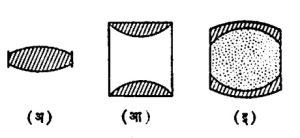
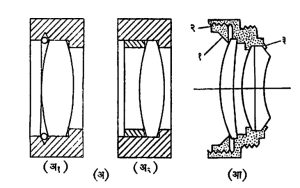
आकारानुसार भिंगाचे वर्गीकरण पुढीलप्रमाणे करतात. मध्यभागी फुगीर व कडेला पातळ असणाऱ्या भिंगांना बहिर्वक्र भिंगे असे म्हणतात. गोलीय बहिर्वक्र भिंगाचे पुढील तीन उपप्रकार होतातः (१) दोन्ही पृष्ठे बहिर्गोल असणारी भिंगे, (२) एक पृष्ठ बहिर्गोल व दुसरे असणारी भिंगे, (३) एक पृष्ठ अतंर्गोल आणि दुसरे बहिर्गोल असणारी चंद्रकोरी भिंगे (आ. १).

याउलट मध्यभागी पातळ व कडेला जाड असणाऱ्या भिंगांना अंतर्वक्र भिंगे असे म्हणतात. गोलीय अंतर्वक भिंगांचेही वरीलप्रमाणेच तीन प्रकार होतात. (आ. २).

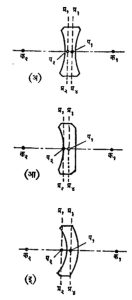
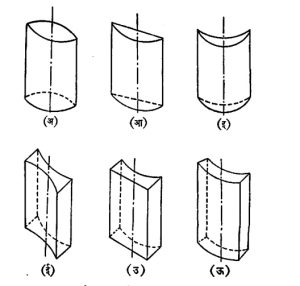
चितीय भिंगे : भिंगाचे वक्रपृष्ठ वृत्तचितीच्या पृषठाच्या छेदाच्या आकाराचे असेल, तर त्याला चितीय भिंग असे म्हणतात. ही भिंगे असे म्हणतात. ही भिंगे अंतर्वक्र अशा दोन्ही प्रकारची असू शकतात आणि वरीलप्रमाणेच त्यांचे प्रत्येकी तीन उपप्रकार होतात (आ. ३). गोलाय पृष्ठांची निर्मिती करणे सुकर असल्याने गोलीय भिंगांची निर्मिती व वापर फार मोठ्या प्रमाणावर होतो. चितीय किंवा इतर अगोलीय भिंगे तयार करणे कठीण असल्याने त्यांची किंमत खूपच जास्त पडते, म्हणून ती फक्त काही खास उपयोगांसाठी वापरली जातात.

चितीय भिंगे अक्षाला समांतर असलेल्या प्रतलातील किरणांचे आभिसरण (केंद्रीकरण) किंवा अपसरण (पसरविणे) यांपैकी काहीच करू शकत नाहीत. आक्षाला लंब असलेल्या प्रतलात बहिर्वक चितीय भिंगाची अभिसारणशक्ती कमाल असून इतर दिशांना हळूहळू कमी होत जाऊन शेवटी अक्ष-समांतर दिशेला ती शून्य होते. अंतर्वक्र भिंगाची अपसरणशक्तीही याचप्रमाणे बदलत जाते.

दृष्टीवैषम्य या नेत्रदोषाचे निराकरण करण्यासाठी योग्य त्या शक्तीचे चितीय भिंग चष्म्यामध्ये वापरावे लागते, इतकेच नव्हे, तर त्या भिंगाच्या अक्षाची दिशाही योग्य तीच ठेवावी लागते [⟶ चष्मा]. ज्योत किंवा तत्सदृश विस्तृत उद्‍गमाची चितीय भिंगामुळे मिळणारी प्रतिमा रेषेच्या आकाराची असते. याचाही काही ठिकाणी उपयोग होतो. (उदा., वर्णपटमापकाच्या फटीवर प्रकाश केंद्रीत करण्यासाठी). सिनेमास्कोप किंवा तत्सदृश रूंद पडद्याच्या चित्रपटाच्या प्रक्षेपणासाठी व चित्रपट तयार करण्यासाठी वापरल्या जाणाऱ्या अँनामॉर्फिक (प्रतिमेचे आकुंचन करणाऱ्या) भिंगांच्या एका प्रकारात चितीय भिंगाचा उपयोग होतो [⟶ चलच्चित्रपट तंत्र]. यासंबंधी थोडी अधिक माहिती पुढे दिली आहे.

चिन्ह-संकेत : वेगवेगळ्या प्रकारच्या भिंगांसाठी व वेगवेगळ्या प्रकारच्या प्रतिमा मिळतात त्या सर्वांसाठी सर्वत्र एकच सूत्र लागू व्हावे याकरिता प्रकाशीय अंतरांना ठराविक पद्धतीने धन वा ऋण चिन्हे द्यावी लागतात. याबद्दलच्या नियमांना ‘चिन्ह-संकेत’ असे म्हणतात. असे वेगवेगळे अनेक चिन्ह-संकेत प्रचारात आहेत. प्रत्येक संकेतात काही सोयी व काही गैरसोयी आहेत. कोणत्याही संकेत वापरल्यास त्याच्याशी सुसंगत अशीच सूत्रे वापरणे आवश्यक असते. येथे वापरण्यास सर्वात सोपा असा ‘खरे धन व भ्रामक (आभासी) ऋण ‘ हा संकेत वापरला आहे. ‘खरा पदार्थ’ म्हणजे जेथून प्रकाशकिरण प्रत्यक्ष निघतात तो बिंदू. ‘खरी प्रतिमा’ म्हणजे जी पडद्यावर पाडता येते ती किंवा जिच्या ठिकाणी प्रकाशकिरण प्रत्यक्ष एकत्र येतात ती. दोहोंची अंतरे या संकेतानुसार धन होतील. उलट भ्रामक पदार्थ किंवा भ्रामक प्रतिमा यांची अंतरे ऋण घ्यावी लागतील. [⟶ प्रकाशकी].

भिगांसंबंधी काही संज्ञा : येथून पुढील सर्व विवरण गोलीय भिगांच्या संदर्भातच केलेले आहे. भिगांच्या संदर्भात वापरल्या जाणाऱ्या महत्त्वाच्या संज्ञांचे थोडक्यात विवेचन येथे केले आहे.

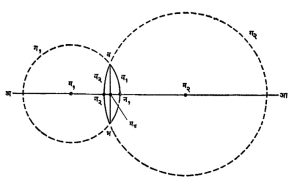
वक्रता मध्य व वक्रता त्रिज्या : भिंगाच्या (एखादा) पृष्ठभाग ज्या संपूर्ण गोलाचा एक भाग असतो त्या गोलाच्या मध्यबिंदूला त्या पृष्ठाचा वक्रता मध्य व त्याच्या त्रिज्येला त्या पृष्ठाची वक्रता त्रिज्या असे म्हणतात. (आ. ४).

प्रधान अक्ष : भिंगाच्या दोन्ही वक्रता मध्यांमधून जाणाऱ्या रेषेला भिंगाचा प्रधान अक्ष किंवा प्रकाशीय अक्ष असे म्हणतात (आ.४). भिंगासंबंधीची सर्व अंतरे या प्रधान अक्षावरून मोजली जातात.

केंद्र व केंद्रांतर : बहिर्गोल भिंगावर प्रधान अक्षाला समांतर अशी किरण शलाका आपाती केली असता भिंगातून बाहेर आल्यावर हे सर्व किरण प्रधान अक्षावर ज्या बिंदूवर एकत्र येतात त्या बिंदूला भिंगाचे (द्वितीय) केंद्र आणि त्या बिंदूच्या भिंगापासूनच्या अंतराला भिंगाचे (द्वितीय) केंद्रांतर (f₂) असे म्हणतात [आ. ५ (अ)]. उलट ज्या बिंदूवर बिंदूमात्र पदार्थ ठेवला असता त्याच्यापासून निघणारे किरण भिंगातून बाहेर पडल्यावर अक्ष-समांतर होतात त्या बिंदूला भिंगाचे प्रथम केंद्र व त्याच्या भिंगापासूनच्या अंतराला प्रथम केंद्रांतर (f₁) असे म्हणतात. भिंगाच्या दोन्ही बाजूंना एकच माध्यम असल्यास प्रथम केंद्रांतर= द्वितीय केंद्रांतर असते.

भिंगावर प्रकाश आपाती होतो त्या बाजूच्या माध्यमाचा प्रणमनांक [⟶ प्रकाशकी] μ₁ व विरूद्ध बाजूच्या माध्यमाचा प्रणमनांक μ₂ असल्यास असे सिद्ध करता येते की, f₁/f₂= μ₁/μ₂. बहिर्गोल भिंगामुळे समांतर किरण खरोखरची (प्रत्यक्षपणे) केंद्रावर एकत्र येतात म्हणून या केंद्राला खरे केंद्र म्हणतात व केंद्रांतराला धन चिन्ह देतात. त्याच प्रमाणे बर्हिगोल भिंगाला अभिसारी भिंग किंवा धन भिंग असेही म्हणतात.

अंतर्गोल भिंगावर समांतर किरण शलाका आपाती झाली असता भिंगातून बाहेर येणारे किरण परस्परांपासून दूर दूर जातात. म्हणून अशा भिंगांना अपसारी भिंगे (किंवा ऋण भिंगे) असे म्हणतात. या दूर जाणाऱ्या किरणांच्या दिशा मागे वाढविल्यास त्या रेषा प्रधान अक्षाला एका बिंदूत छेदतात [आ. ५(आ)]. या बिंदूला त्या भिंगाचे भ्रामक केंद्र व त्याच्या भिंगापासूनच्या अंतराला (द्वितीय) भ्रामक केंद्रांतर असे म्हणतात या केंद्रांतराला ऋण चिन्ह देतात.

छिद्रव्यास : भिंगाची एकूण मर्यादा रेषा (सामान्यपणे) वर्तुळाकार असते. या वर्तुळाच्या व्यासाला छिद्रव्यास (d) किंवा रंध्रव्यास असे म्हणतात. हा जितका मोठा असेल तितका जास्त प्रकाश भिंगावर पडतो व मिळणारी प्रतिमा जास्त तेजस्वी असते.

भिंग शक्ती : भिंगाचे केंद्रांतर मीटरमध्ये व्यक्त करून त्याचा व्यस्तांक घेतल्यास मिळणाऱ्या संख्येला भिंग शक्ती (P) असे म्हणतात व ती डायॉप्टर या एककात देतात. उदा., केंद्रांतर +५० सेमी. असल्यास, +५० सेंमी. = + ०.५ मी. भिंग शक्ती P = १/+०.५ = +२ डायॉप्टर. बहिर्गोल भिंगांच्या शक्ती धन व अंतर्गोल भिंगांच्या ऋण चिन्हांकित असतात. नेत्रवैद्य आपणाला जो चष्म्याचा ‘नंबर’ देतो, तो नंबर म्हणजे चष्म्यासाठी वापरावयाच्या भिंगांची शक्ती (डायॉप्टरमध्ये) असते. उदा., चष्म्याचा नंबर –२.५ असल्यास P = –२.५ f = १/–२.५ = –०.४ मी. = –४० सेंमी. म्हणजे ४० सेंमी. केंद्रांतर असलेले अंतर्गोल भिंग वापरले पाहिजे.

सापेक्ष छिद्रव्यास : भिंगाचे केंद्रांतर व त्याचा छिद्रव्यास यांच्या गुणोत्तराला (= f/d) सापेक्ष छिद्रव्यास असे महणतात. उदा., भिंगाचे केंद्रांतर छिद्रव्यासाच्या २.५ पट असल्यास त्याचा सापेक्ष छिद्रव्यास २.५ येईस.

केंद्रांक : सापेक्ष छिद्रव्यासाच्या संख्यात्मक मूल्याला भिंगाचा केंद्रांक किंवा f – क्रमांक असेही म्हणतात. वरील उदाहरणातील भिंगाचा केंद्रांक २.५ येईल. केंद्रांकाला भिंगाचा ‘वेग’ असेही म्हणतात. छायाचित्रणाच्या परिभाषेत हा अंक f/२.५ असा व्यक्त करतात. केंद्रांक जितका लहान तितका भिंगाचा वेग जास्त व तितके छायाचित्र घेण्यासाठी लागणारे उद्‍भासन (फिल्मवर प्रकाश पडण्याचा कालावधी) कमी लागते. [⟶ कॅमेरा].

प्रकाशीय मध्य : भिंगामध्ये असा एक बिंदू असतो की , त्याच्यामधून आपाती किरण जात असेल, तर भिंगातून बाहेर येताना त्या किरणाची दिशा बदलत नाही. या बिंदूला प्रकाशीय मध्य म्हणतात.

पातळ भिंग : भिंगाची जाडी (त्याच्या केंद्रांतराच्या तुलनेने) अत्यंत कमी असल्यास त्याला पातळ भिंग असे म्हणतात. अशा भिंगाच्या बाबतीत कित्येक सोपी सूत्रे लागू पडतात. भिंगाची जाडी जास्तीत जास्त केंद्रांतराच्या एक सप्तमांश असेल, तर त्याला आदर्श पातळ भिंगाची सूत्रे लागू करून येणाऱ्या उत्तरात सु. ०.१% इतकी चूक येते. ही पुष्कळ प्राथमिक गणितकृत्यात दुर्लक्षणीय मानता येते. म्हणून ही पातळी भिंगाची कल्पना अत्यंत उपयुक्त ठरली आहे.

पातळ भिंगासाठी सूत्रे : हवेत ठेवलेल्या पातळ भिंगाच्या दोन पृष्ठांच्या वक्रता त्रिज्या अनुक्रमे r₁ व r₂ असून भिंगाच्या द्रव्याचा प्रणमनांक μअसेल, तर त्याचे केंद्रांतर (f) पुढील सूत्राने दिले जाते : 

1/f = (μ- 1) {1/r₁ + 1/r₂}      …        …        …        (१)

या सूत्राला ‘भिंगे तयार करणाऱ्यांचे सूत्र’ असे म्हणतात. इष्ट केंद्रांतराचे भिंग तयार करण्यासाठी त्याच्या पृष्ठांच्या वक्रता त्रिज्यांची निवड या सूत्राच्या साहाय्याने करता येते.

भिंगापासून u या अंतरावर बिंदुमात्र वस्तू भिंगाच्या प्रधान अक्षावर ठेवल्यास मिळणाऱ्या प्रतिमेच्या भिंगापासूनचे अंतर v पुढील सूत्राने दिले जाते.

1/u + 1/v =1/f         …        …        …        (२)

ही सर्व अंतरे भिंगाच्या प्रकाशीय मध्यापासून मोजली आहेत असे मानले जाते परंतु भिंग पातळ असल्यास अंतरे कोणत्याही पृष्ठापासून मोजली तरी विशेषशी चूक येत नाही.

पातळ व दोन्ही पृष्ठाभागांच्या वक्रता त्रिज्या समान असलेल्या बहिर्गोल भिंगाच्या बाबतीत वस्तूचे स्थान आणि त्यानुरूप मिळणाऱ्या प्रतिमेचे स्थान व तिचे स्वरूप यांसंबंधीची माहिती कोष्टक क्र. १ मध्ये दिली आहे.

कोष्टक क्र. १. बहिर्गोल भिंगासाठी वस्तू व प्रतिमा यांची स्थाने
वस्तूचे स्थान	प्रतिमेचे स्थान	प्रतिमेचे स्वरूप
अनंत अंतरावर (u⟶∞)	(द्वितीय) केंद्रावर (v=f)	उलटी, खरी व लहान
वक्रता मध्याच्या पलीकडे (r < u < ∞)	(द्वितीय) केंद्र व (द्वितीय) वक्रता मध्य यांच्या दरम्यान (f < v < r)	उलटी, खरी व लहान
वक्रता मध्यावर (u=r)	(द्वितीय) वक्रता मध्यावर (v=r)	उलटी, खरी व वस्तूएवढ्याच आकाराची
वक्रता मध्य व (प्रथम) केंद्र यांच्या दरम्यान (f < u < r)	(द्वितीय) वक्रता मध्यापलीकडे (r < v < ∞)	उलटी, खरी व वर्धित
(प्रथम) केंद्रावर (u=f)	फार दूर (v⟶∞)	उलटी, खरी व वर्धित
(प्रथम) केंद्र व प्रकाशीय केंद्र यांच्या दरम्यान (o < u < f)	पदार्थाच्याच बाजूस (v ऋण)	सुलटी, भ्रामक व वर्धित

अंतर्गोल भिंगाच्या बाबतीत वस्तू कोठेही ठेवली, तरी मिळणारी प्रतिमा सुलटी, आकारमानाने वस्तूपेक्षा लहान व भ्रामक असते. ही प्रतिमा नेहमी भिंगाच्या ज्या बाजूस वस्तू असेल त्याच बाजूकडे मिळते.

न्यूटन सूत्र : वस्तू आणि प्रतिमा यांची अनुक्रमे प्रथम व द्वितीय केंद्रांपासूनची अंतरे x₁ व x₂ असतील, तर न्यूटन यांनी असे दाखविले की,

x₁ x₂ = f²      …         …          …          (३)

याला न्यूटन सूत्र असे म्हणतात. जाड भिंग किंवा दोन वा अधिक भिंगांनी तयार होणाऱ्या भिंग-प्रणालीचे परिणामी केंद्रांतर काढण्यासाठी हे सूत्र विशेष उपयोगी पडते. कारण अशा परिस्थितीत वरील (२) या सूत्राचा उपयोग करावयाचा म्हटल्यास u व v ही अंतरे प्रणालीवरील कोणत्या बिंदूपासून मोजावीत याचा निर्णय करता येत नाही परंतु प्रयोगाने केंद्रबिंदू सहज काढता येतात व म्हणून x₁ व x₂ ही अंतरे निश्चितपणे मोजता येतात.

वर्धन : भिंगाच्या प्रधान अक्षावर ठेवलेल्या वस्तूची (अक्षलंब दिशेने) उंची h₁ असेल व त्याच्या प्रतिमेची उंची h₂ असेल, तर ^h2 / _h1 या गुणोत्तराला प्रतिमेचे वर्धन (m) असे म्हणतात. भूमितीवरून असे सिद्ध करता येते की,

m =	h2	=	v	…      …         …         (४)
	h1		u

जाड भिंग :प्रधान प्रतले : व्यवहारात वापरली जाणारी भिंगे अनेकदा पातळ मानता येत नाहीत. प्रतिमेत येणाऱ्या कित्येक दोषांचे निराकरण करून निर्दोष प्रतिमा मिळविण्यासाठी एका भिंगाऐवजी अनेक भिंगांची मालिका म्हणजेच भिंग-प्रणाली वापरावी लागते. अशा परिस्थितीत u, v, f इ. अंतरे कोठून मोजावयाची याबद्दल संदेह उत्पन्न होतो.

प्रयोगावरून असे दिसून येते की, जाड भिंगे व भिंग-प्रणाली यांच्याशी संलग्‍न अशी दोन काल्पनिक प्रतले असून या प्रतलांचे असे वैशिष्ट्य आहे की, u, v, f ही अंतरे या प्रतलांपासून मोजली, तर मग भिंगाला व भिंग-प्रणालीला वरील समीकरण (२) हे बरोबर लागू पडते. या प्रतलांना त्या भिंगाची किंवा भिंग-प्रणालीची ‘प्रधान प्रतले’ असे म्हणतात. (आ.१ व २ मध्ये विविध आकारच्या जाड भिंगांची प्रधान प्रतले तुटक रेषांनी दाखविली आहेत). या प्रतलांची स्थाने प्रयोगाने काढता येतात. आ. १ व २ मधील प्र_१प्र_२ या प्रतलाला प्रथम प्रधान प्रतल व प्र_३प्र_४ या प्रतलाला द्वितीय प्रधान प्रतल असे म्हणतात. भिंगाच्या डाव्या बाजूकडील अंतरे प्रथम प्रधान प्रतलापासून व उजवीकडील अंतरे द्वितीय प्रधान प्रतलापासून मोजली जातात.

आधारभूत बिंदू : कोणत्याही भिंगाच्या अथवा भिंग-प्रणालीच्या बाबतीत जे बिंदू ज्ञात असतील, तर त्या प्रणालीचे प्रकाशीय गुणधर्म पूर्णपणे माहीत होतात त्या बिंदूंना त्या प्रणालीचे आधारभूत बिंदू असे म्हणतात. सामान्यपणे आधारभूत बिंदू सहा आहेत व ते पुढीलप्रमाणे आहेत : (१) प्रणालीचे दोन्ही केंद्रबिंदू, (२) दोन्ही प्रधान बिंदू व (३) दोन शृंग बिंदू. केंद्रबिंदूचे स्पष्टीकरण वर आलेच आहे. प्रधान प्रतले ज्या दोन बिंदूंत प्रणालीच्या प्रधान अक्षाला छेदतात (आ. १ व २ मधील प_१ व प_२ हे बिंदू) त्यांना प्रणालीचे प्रधान बिंदू असे म्हणतात. त्याचप्रमाणे भिंग-प्रणालीशी संलग्‍न असे दोन बिंदू असतात की, आपाती किरणाची दिशा त्यातील पहिल्या बिंदूतून जात असेल, तर निर्गत किरणाची दिशा दुसऱ्या बिंदूमधून जाते व ती आपाती किरणाला समांतर असते. या बिंदूंना शृंग बिदूं म्हणतात. प्रणालीच्या दोन्ही बाजूंचे माध्यम एकच असेल, तर (सामान्यपणे प्रणालीच्या दोन्ही बाजूंना हवा हे एकच माध्यम असते) शृंग बिंदू व प्रधान बिंदू हे समानुपाती (एकरूप) असतात.

भिंग-प्रणाली : एकाकी भिंगे वापरल्यास मिळणाऱ्या प्रतिमांत अनेक वैगुण्ये आलेली दिसतात [⟶ प्रकाशीय व्यूहांतील विपथन]. त्याचप्रमाणे केव्हा केव्हा अपेक्षित वर्धन करू शकणाऱ्या भिंगाच्या केंद्रांतराचे मूल्य सोयीस्कर नसते. या अडचणींचे निराकरण करण्यासाठी सर्व उच्च दर्जाच्या प्रकाशीय उपकरणांत एका भिंगाऐवजी सममूल्य भिंगांची मालिका म्हणजेच भिंग-प्रणाली वापरण्यात येतात. अशा प्रणालीतील सर्व भिंगांचे प्रधान अक्ष समानुपाती असावे लागतात.

काही प्रणालींमध्ये घटक भिंगे एकमेकांना चिकटून ठेवलेली असतात उदा., विवर्ण भिंग [⟶ प्रकाशीय व्यूहांतील विपथन]. अशा दोन भिंगांच्या प्रणालीचे परिणामी केंद्रांतर F असल्यास व घटक भिंगांची केंद्रांतरे अनुक्रमे f₁ व f₂ असल्यास असे सिद्ध करता येते की,

1	=	1	+	1	…           …            …           (५)
F		f1		f2

या सूत्रात केंद्रांतरांची चिन्हे चिन्ह-संकेतानुसार योग्य ती घेणे आवश्यक आहे. प्रणालीमध्ये दोहोंपेक्षा अधिक घटक भिंगे असल्यास वरील सूत्रात उजव्या बाजूला त्या सर्वांच्या केद्रांतरांच्या व्यस्तांकांची बेरीज घ्यावी लागेल.

काही प्रणालींमधील घटक भिंगांमध्ये काही निश्चित अंतरे ठेवलेली असतात उदा., कॅमेऱ्याची भिंगे किंवा सूक्ष्मदर्शकाचे वस्तुभिंग. सूक्ष्मदर्शकाची व दूरदर्शकाची नेत्रभिंगे अनेकदा परस्परांमध्ये काही अंतर ठेवलेली बहिर्गोल भिगांची जोडी असते. [⟶ कॅमेरा दूरदर्शक सूक्ष्मदर्शक].

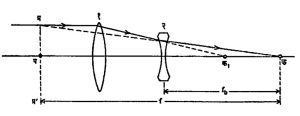
भिंग-जोडी : f₁ व f₂ ही केंद्रांतरे अनुक्रमे असलेली दोन भिंगे त्यांच्यामध्ये d हे अंतर ठेवून समाक्ष बसविलेली आहेत असे समजू (आ. ६). या प्रणालीचे परिणामी केंद्रांतर (F) व प्रधान प्रतले यांविषयी विवरण केले असता प्रणालींची कार्य पद्धती समजून येईल. त्याचप्रमाणे प्रधान प्रतलांची उपयुक्तताही स्पष्ट होईल.

अआ हा अक्ष-समांतर किरण पहिल्या भिंगावर पडून बाहेर येताना त्याची दिशा आई ही अशी असेल की, तो क_१ या (केंद्र) बिंदूमध्ये अक्षाला छेदेल परंतु ई येथे दुसऱ्या भिंगामध्ये प्रणमन झाल्यामुळे तो प्रत्यक्षात क येथे अक्षाला छेदतो. याचप्रमाणे प्रणालीवर डावीकडून आपाती होणारे सर्व अक्ष-समांतर किरण क येथे अक्षाला मिळतील म्हणजेच, क हा प्रणालीचा परिणामी द्वितीय केंद्रबिंदू आहे (त्याचप्रमाणे क ‘ हा प्रणालीचा प्रथम केंद्रबिंदू आहे हे दाखविता येईल).

अआ व कई या रेषा वाढविल्या असता परस्परांना इ या बिंदूत मिळतात. म्हणजे जणू काही अआ हा किरण सरळ इ पर्यंत येतो व मग इईक या मार्गाने केंद्रावर जातो. इ मधून प्र_३प_२प्र_४ हे प्रतल अक्षाला लंब दिशेने काढले असून ते अक्षाला प_२ या बिंदूत छेदते. प्र_३प्र_४ हे द्वितीय प्रधान प्रतल व प_२ हा द्वितीय प्रधान बिंदू आहे. त्याचप्रमाणे प्र_१प_१प्र_२ हे प्रथम प्रधान प्रतल व प_१ हा प्रथम प्रधान बिंदू आहे.

प_२क या अंतराला प्रणालीचे द्वितीय केंद्रांतर (F₂) व प_१क’ हे प्रथम केंद्रांतर (F₁) आहे. F₁ = F₂ = F हे सहज सिद्ध करता येते. त्याचप्रमाणे

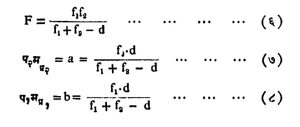
हेही सिद्ध करता येते. (७) व (८) या सूत्रांच्या साहाय्याने २ आणि १ या भिंगांच्या संदर्भात दोन्ही प्रधान बिंदूंची स्थाने निश्चित होतात. म_प्र२क या अंतराला प्रणालींचे पार्श्व केंद्रांतर असे म्हणतात.

प्रधान प्रतलांचे उपयोग : विशिष्ट प्रणालीमध्ये कितीही (बहिर्गोल व अंतर्गोल यांपैकी कोणत्याही प्रकारची) भिंगे असली, तरी प्रणालीच्या प्रधान प्रतलांची व दोन्ही केंद्रबिंदूंची स्थाने माहीत असल्यास प्रणालीच्या अक्षावर कोठेही ठेवलेल्या वस्तूची प्रतिमा कोठे व कशा प्रकारची पडेल ते किरण-आकृती काढून निश्चित करता येते. त्यासाठी प्रत्येक घटक भिंगात होणाऱ्या प्रणमनाचा वेगवेगळा विचार करण्याचे कारण पडत नाही. परिणामी केंद्रांतरे त्या त्या प्रधान प्रतलापासून मोजावयाची असतात, हे लक्षात घ्यावयास हवे. प्रणालींमुळे निर्माण होणाऱ्या प्रतिमेचे वर्धन या परिणामी केंद्रांतरावर अवलंबून असते. प्रणालीतील शेवटच्या भिंगापासून द्वितीय केंद्रापर्यंतच्या अंतराला पश्च केंद्रांतर असे म्हणतात.

दूरचित्रण (टेलिफोटो) भिंग : कॅमेऱ्याची लांबी आटोपशीर राहण्यासाठी त्याच्या भिंगाचे केंद्रांतर कमी ठेवावे लागते परंतु अती दूरच्या वस्तूचे भिंगामुळे तयार होणाऱ्या प्रतिमेचे आकारमान भिगाच्या केंद्रांतराच्या सम प्रमाणात असते. म्हणून अशा दूरच्या वस्तूची प्रतिमा फिल्मवर मोठी मिळावी यासाठी भिंगांचे केंद्रांतर वाढवावयास हवे. या परस्पर विरोधी अटींमधून मार्ग काढण्यासाठी सुयोग्य भिंगांची प्रणाली घेऊन तिचे परिणामी केंद्रांतर मोठे (मोठी प्रतिमा मिळण्यासाठी) परंतु पश्च केंद्रांतर कमी (कॅमेऱ्याची लांबी कमी होण्यासाठी) असेल अशी व्यवस्था करता येते. अशा रचनेला दूरचित्रण भिंग असे म्हणतात. आ. ७ मध्ये अशा भिंगाचे तत्त्व स्पष्ट केले आहे. या प्रणालीत एक बहिर्गोल भिंग व एक अंतर्गोल भिंग परस्परांपासून काही अंतर ठेवून बसवलेली असतात. त्यांची केंद्रांतरे आणि त्यांच्यामधील अंतर असे ठेवतात की, प्रणालीचे दुसरे प्रधान प्रतल प्रणालीच्याही बरेच पुढे (म्हणजे छायाचित्रित करावयाची वस्तू ज्या बाजूला असेल त्या बाजूला) येते. त्यामुळे या प्रणालीचे परिणामी केंद्रांतर मोठे असूनही पश्च केंद्रांतर कमी राहते. उच्च प्रतीच्या दूरचित्रण भिंगामध्ये आ. ७ मधील प्रत्येक भिंगाऐवजी समतुल्य संयुक्त भिंगे वापरतात [⟶ कॅमेरा]. छायाचित्रणासाठी वापरल्या जाणाऱ्या झूम भिंगे, बायागॉन भिंगे व इतर खास भिंगप्रणालींच्या माहितीसाठी ‘कॅमेरा’ ही नोंद पहावी. दूरदर्शक व सूक्ष्मदर्शक यांत वापरल्या जाणाऱ्या नेत्रभिंगसमूहांबद्दलच्या माहितीसाठी ‘ दूरदर्शक’ व ‘ सूक्ष्मदर्शक’ या नोंद पहाव्यात.

प्रतिमावर्धक : वस्तूंचे बारीकसारीक तपशील स्पष्टपणे दिसण्यासाठी प्रतिमावर्धकाचा उपयोग करतात. उदा., घड्याळाची दुरूस्ती करणारे, जवाहिराची परीक्षा करणारे लोक प्रतिमावर्धकाचा वापर करतात. याच्या साहाय्याने मूळ वस्तूपेक्षा सु. तीन ते वीस पट मोठी प्रतिमा मिळू शकते. याचे कार्य सूक्ष्मदर्शकासारखेच असते पण ते सहज जवळ बाळगता येण्याइतके आटोपशीर व किंमतीला कमी असल्याने त्याला ‘साधा सूक्ष्मदर्शक’ असेही म्हणतात.

यासाठी फक्त एक बहिर्गोल भिंग वापरता येते. हे भिंग पाहणाऱ्याच्या डोळ्याला अगदी लगत धरतात. पहावयाच्या वस्तूचे भिंगापासूनचे अंतर (भिंग अथवा डोळा मागे पुढे करून) असे साधतात की, त्या वस्तूची भ्रामक पण वर्धित प्रतिमा भिंगातून (सु.) २५ सेंमी.वर तयार व्हावी. पहाणारा प्रत्यक्षात ही प्रतिमाच पाहत असतो. भिंगाचे केंद्रांतर f सेंमी. असल्यास या प्रतिमावर्धकाची वर्धनक्षमता M = १+२५ /f असे दाखविता येते. वर्धनक्षमता वाढविण्यासाठी कमी केंद्रांतराचे भिंग वापरल्यास प्रतिमेतील गोलीय विपथन [⟶ प्रकाशीय व्यूहांतील विपथन] हा दोष वाढतो. हा दोष व वर्णविपथनाचा दोष कमी करण्यासाठी संयुक्त भिंगे वापरली जातात. (आ. ८).

प्रतिमा (सु. २५ सेंमी.) अंतरावर तयार झाल्यास वर्धनक्षमता कमाल मिळते व वस्तू जास्तीत जास्त स्पष्ट दिसते. म्हणून या अंतराला जास्तीत जास्त स्पष्टतेचे अंतर असे म्हणतात.प्रतिमा अनंत अंतरावर तयार झाल्यास निरीक्षण करण्यात डोळ्यावर पडणारा ताण किमान होतो पण या परिस्थितीत वर्धनक्षमता काहीशी कमी म्हणजे २५/f इतकी मिळते. भिंगे तयार करणारे कारखानदार सामान्यतः हीच क्षमता देतात. विशिष्ट भिंगाची वर्धनक्षमता समजा ५ असेल, तर ती ५ ´ अशी दर्शवतात.

भिंगनिर्मिती :प्रकाशीय काच : नेहमीच्या वापरात असलेल्या काचेच्या वस्तू (उदा., निरनिराळ्या लहान मोठ्या बाटल्या, बरण्या, पेले, खिडक्यांची तावदाने वगैरे) ह्या व्यापारी व सामान्य काचेच्या बनविलेल्या असतात पण दूरदर्शक, सूक्ष्मदर्शक, कॅमेरे यांसारख्या उपकरणांना लागणारी विविध प्रकारची भिंगे, वर्णपटमापकासाठी लागणारे लोलक व अनेक प्रकाशीय प्रयोगांसाठी व उपयोगासाठी लागणारे सपाट तसेच वक्र आरसे बनविण्यासाठी लागणाऱ्या खास काचेस प्रकाशीय काच म्हणतात.

व्यापारी काच व प्रकाशीय काच यांच्या घटकद्रव्यांत बराचसा फरक असतो हे खरे, तरी ह्या दोन प्रकारच्या काचांतील महत्त्वाचा फरक पुढीलप्रमाणे आहे. व्यापारी काचेस लागणारी निरनिराळी घटकद्रव्ये त्यांच्या त्यांच्या प्रमाणानुसार घेऊन एकमेकांत उत्तम प्रकारे मिसळवितात व मगच भट्टीत वितळविण्यासाठी घालतात. द्रव्ये वितळत असताना होणारे संवहन प्रवाह व विसरण (द्रव्ये एकमेकांत मिसळणे) यांशिवाय दुसरी क्रिया केली जात नाही. भट्टीत रस थंड करण्याऐवजी तीतील रस काढून निरनिराळ्या प्रकारच्या वस्तू तयार करतात व त्या वस्तू सावकाश थंड करतात. याउलट प्रकाशीय काच तयार करताना द्रव्ये योग्य प्रमाणात चांगल्या तऱ्हेने मिसळून भट्टीत घातल्यावर व रस तयार झाल्यावर यांत्रिक पद्धतीने तो रस कित्येक तास ढवळीत ठेवतात आणि भट्टीतच निवांतपणे थंड होण्यासाठी ठेवून देतात.

प्रकाशीय काच प्रामुख्याने एकजिनसी, समदिक् (जिचे भौतिक गुणधर्म दिशेनुसार बदलत नाहीत अशी), बव्हंशी रंगहीन व स्वच्छ असावी लागते. तिच्यात बारीक कण वा बुडबुडे नसावेत. ती यांत्रिक व रासायनिक दृष्ट्या स्थिर असणे आवश्यक असते म्हणजेच तिच्यात अंतर्गत ताण नसावेत व हवेतील घटकांचा तिच्यावर रासायनिक परिणाम होता कामा नये. तिच्या अंगी उजाळा किंवा चकाकी घेण्याची क्षमता पाहिजे आणि सर्व दिशांनी तिचा प्रणमनांक सारखा असणे जरूर असते. प्रकाशातील ज्या तरंगलांबीच्या पट्ट्याकरीता ती काच तयार केलेली असेल त्या तरंगलांबीच्या प्रारित (तरंगरूपाने आपाती झालेल्या) ऊर्जा काचेतून संक्रमित (किंवा तिच्या पृष्ठभागावरून परावर्तित) झाल्या पाहिजेत. प्रकाशीय काचेतून प्रकाशाचे आधिक प्रमाणात संक्रमण होणे तसेच तिचा प्रणमनांक मोठा असणे आवश्यक असते. हे दोन्ही गुण प्रकाशाच्या तरंगलांबीनुसार बदलतात.

दृश्य प्रकाशाकरिता वापरण्यास उपयुक्त अशा या काचेच्या वस्तूंचे (उदा., भिंगे, लोलक वगैरे) गुणधर्म प्रामुख्याने प्रणमनांक व सापेक्ष अपस्करण व्यस्तांक (प्रणमनामुळे लघुतर व दीर्घतर तरंगलाब्यांच्या प्रकाशाचे एखाद्या काचेमुळे होणारे अलगीकरण दर्शविणारा अंक) म्हणजेच अर्न्स्ट ॲबे या जर्मन भौतिकीविज्ञांच्या नावाने ओळखला जाणारा ॲबे अंक किंवा न्यू मूल्य या दोन संख्यांनी दर्शविले जातात. υ मूल्याची व्याख्या पुढीलप्रमाणे करतात.

υ =	μD–1
	μF – μC

येथे μ_D, μ_F व μ_C हे दिलेल्या काचेचे अनुक्रमे सोडियमाच्या वर्णपटातील D या रेषेची तरंगलांबी आणि हायड्रोजन वर्णपटातील F व C या रेषांच्या तरंगलांब्या यांच्या बाबतीतील प्रणमनांक आहेत [⟶ वर्णपटविज्ञान]. प्रकाशीय काचेचे निरनिराळे μ_D–1 : υ या दोन संख्या देऊन तिचे निरनिराळे प्रकार निर्देशित करण्याचा प्रघात आहे. उदा., एका काचेच्या μ_D= १.५१७  व υ = ६४.५ आहे, तर अशा काचेच्या प्रकाराचे μ_D–1 : υ म्हणजे ५१७ : ६४५ असे निर्देशन करतात.

प्रकाशीय काचेचे स्थूलमानाने दोन प्रकार मानले जातात : (१) क्राउन व (२) फ्लिंट. क्राउन काचांची υ मूल्ये ५० किंवा त्याहून अधिक असतात, तर फ्लिंट काचांची υ मूल्ये ५० पेक्षा कमी असतात. दूरदर्शकांना लागणारी मोठ्या छिद्रव्यासाची विशिष्ट प्रकारची भिंगे त्याचप्रमाणे सूक्ष्मदर्शकांसाठी लागणारी भिंगे काही खास प्रकारच्या काचेची बनवितात. या काचेत बेरियम ऑक्साइड, बोरेट किंवा बोरिक ॲनहायड्राइड व जास्त प्रमाणात लेड ऑक्साइड वापरतात. कोष्टक क्र. २ मध्ये काही प्रकाशीय काचांची घटकद्रव्ये व μ_D-1: υ मूल्ये दिलेली आहेत.

लँथॅनम काचा : वरील सर्व प्रकारच्या काचांमध्ये सिलिकॉन डाय-ऑक्साइड (SiO₂) हा प्रमुख घटक आहे. १९५० मध्ये सी. डब्ल्यू. मोरी यांनी असे शोधून काढले की, SiO₂ च्या ऐवजी ⇨ विरल मृत्तिकांच्या ऑक्साइडांचा उपयोग केल्यास फारच उच्च दर्जाची प्रकाशीय काच मिळते. या काचांना सामान्यतः लँथॅनम काचा असे म्हणतात, तरी त्यांमध्ये थोड्या प्रमाणात लँथॅनमाशिवाय इतर काही विरल मृत्तिकांचाही समावेश केलेला असतो. या काचांच्या भिंगामुळे तयार होणाऱ्या प्रतिमांमधील विपथन फारच चांगल्या तऱ्हेने जवळजवळ नष्ट करता येते. हल्ली सर्व भारी कॅमेऱ्यांची भिंगे लँथॅनम काचांचीच केलेली असतात. या काचांच्य़ा शोधामुळे प्रकाशीय उपकरणांच्या गुणवत्तेत आश्वर्यकारक सुधारणा करणे शक्य झाले आहे. वेगवेगळ्या कारखान्यांनी तयार केलेल्या प्रकाशीय काचांच्य़ा गुणधर्मांत सुसंगता आणण्यासाठी ‘नाटो’ या संघटनेच्या सहकार्याने या काचांच्या घटकद्रव्यांचे प्रमाणीकरण करण्यात आले असून त्यांना वेगवेगळे सांकेतिक क्रमांक देण्यात आले आहेत.

पूर्वीच्या काळी प्रकाशीय काचेची घटकद्रव्ये मृत्तिकेच्या मुशात वितळवून काच तयार करीत परंतु यामध्ये मुशीच्या द्रव्यापैकी काही भाग द्रव काचेत विरघळतो व त्यामुळे काचेचे गुणधर्म बदलतात, असे आता दिसून आले आहे म्हणून या कामासाठी आता प्लॅटिनमाच्या मुशी वापरतात. अशा किंमती काचेपासून भिंगे तयार करताना उगाळून वाया जाणाऱ्या काचेचे प्रमाण किमान ठेवणे इष्ट असते. यासाठी योग्य त्या काचेचा तुकडा मऊ होईतो तापवितात व मग साच्यात दाबून त्याला इष्ट भिंगाचा आकार (परंतु भिंगापेक्षा थोडा मोठा) स्थूलमानाने देतात. त्यामुळे पुढे कराव्या लागणाऱ्या उगाळण्याच्या क्रियेचे प्रमाणही कमी होते.

कोष्टक क्र. २. काही प्रकाशीय काचांची घटकद्रव्ये (%) व μD-1: υ मूल्य
घटक द्रव्ये⟶ काचेचा प्रकार ↓	SiO2	B2O3	Al2O3	PbO	CaO	ZnO	BaO	Na2O	K2O	μD–1: υ मूल्य
बोरोसिलिकेट क्राउन	७०.४	७.५	–	–	२.०	–	–	५.३	१४.५	५१०:६३४
कठीण क्राउन	७४.६	–	–	–	५.०	–	–	९.०	११.०	५०१:६०२
दृढ घट्ट बेरियम क्राउन	३९.६	६.५	२.५	–	–	९.०	४२.०	–	–	६१०:५६७
अदृढ फ्लिंट	५३.३	०.८	–	३३.५	–	–	–	४.०	८.०	५८०: ४१०
दृढ फ्लिंट	४६.१	–	–	४५.१	–	–	–	१.७	६.८	६१६: ३६६
अतिदृढ फ्लिंट	३४.७	–	–	६१.०	–	–	–	१.५	२.५	७१७: २९५

खास गुणधर्मांच्या काचा : प्रतिमा क्षेपकात किंवा शोध दीपात [⟶ प्रकाशक्षेपक] वापरल्या जाणाऱ्या भिंगांना तापमानात एकदम होणाऱ्या वाढीला तोंड द्यावे लागते. म्हणून या ठिकाणी उष्णतेने होणारे प्रसरण अत्यंत कमी असणाऱ्या द्रव्याच्या काचा वापराव्या लागतात. सामान्यतः बोरोसिलिकेट काचा येथे उपयोगी पडतात. शुद्ध SiO₂ वितळवून केलेल्या काचेचाही प्रसरण गुणांक अत्यंत कमी असतो. जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील अदृश्य) किंवा अवरक्त (दृश्य वर्णपटातील तांबड्या रंगाच्या अलीकडील अदृश्य) किरणाच्या साहाय्याने छायाचित्रे घेणाऱ्या कॅमेऱ्यांची भिंगे त्या त्या किरणांना पारदर्शक असावी लागतात. त्याचप्रमाणे सर्वसामान्य काचांवर किरणोत्सर्गी (अतिशय भेदक कण वा किरण बाहेर टाकणाऱ्या) द्रव्यापासून येणारे किरण पडल्यास काचेला तांबूस-काळपट रंग येतो. अशा किरणांशी संपर्क येणऱ्या भिंगाच्या काचेत सिरियम हे द्रव्य समाविष्ट केले असता त्यांना हा रंग येत नाही. चष्म्याच्या भिंगासाठी वापरल्या जाणाऱ्या काचेतून डोळ्याला त्रासदायक होणारे अवरक्त व जंबुपार किरण पलीकडे जाऊ नयेत, यासाठी त्यांच्या काचेत अल्प प्रमाणात लोह समाविष्ट करतात.

प्लॅस्टिके : इष्ट वक्रतेची प्लॅस्टिकाची भिंगे साच्यामधून दाबून हव्या त्या आकाराच्या पृष्ठांची बनविता येतात. त्यांचे वजनही कमी असते. त्यामुळे आता (हलक्या दर्जाच्या) कॅमेऱ्यातून प्लॅस्टिकाची भिंगे वापरण्यात येत आहेत. मिथिलमेथॅक्रिलेट व पॉलिस्टायरीन यांसारखी प्लॅस्टिके यासाठी वापरतात [⟶ प्लॅस्टिक व उच्च बहुवारिके]. प्रकाशीय काच वापरून ज्या आकारांची भिंगे तयार करता येणे अशक्य आहे अशा आकाराची प्लॅस्टिकाची भिंगे अमेरिकेतील पोलरॉइड कंपनी तयार करीत आहे.

द्रवरूप भिंगे : दोन भिंगांच्या मध्ये पारदर्शक द्रवाचा थेंब ठेवून द्रवरूप भिंग तयार करतात. शुद्ध पाणी किंवा ग्लिसरीन वापरून उत्तम द्रवरूप भिंग तयार करता येते. या द्रवाचा प्रणमनांक कमी असल्यामुळे निरनिराळ्या पारदर्शक द्रवांचे मिश्रण करून प्रणमनांक वाढविला जातो आणि असे द्रव भिंग तयार करण्यासाठी वापरतात. भिंगाच्या द्रवाचे लवकर बाष्पीभवन होणार नाही अशी काळजी घेणे आवश्यक असते. द्रवरूप भिंगे जीवविज्ञानातील अभ्यासाकरिता लागणाऱ्या सूक्ष्मदर्शकात वापरतात. सूक्ष्म वस्तुयुक्त पट्टिका व सूक्ष्मदर्शकाचे वस्तुभिंग यांमध्ये द्रवाच्या थेंबाने द्रवरूप भिंग तयार करतात. द्रवरूप भिंगाने सूक्ष्मदर्शकाची वर्धनक्षमता वाढविता येते.

भिंगे तयार करण्याच्या पद्धती : प्रथम इष्ट भिंगाच्या आकारमानापेक्षा थोडा मोठा असा प्रकाशीय काचेचा तुकडा घेतात व उगाळून त्याच्या दोन्ही पृष्ठांना योग्य तो आकार देऊन भिंग तयार करतात. उगाळण्याची क्रिया सामान्यतः तीन टप्प्यांत केली जाते : (१) स्थूलमानीय उगाळणे : ही क्रिया हिऱ्याची पूड लावलेल्या हत्याराच्या साहाय्याने अथवा जाड एमरी किंवा कार्बोरंडम पूड वापरून करतात. यामुळे घासण्याची क्रिया खूप जलद होते व सु. एक मिनिटातच जवळजवळ इष्ट आकाराचे पृष्ठ तयार होते परंतु तुलनेने हे पृष्ठ फारच खडबडीत असते. (२) सूक्ष्ममानीय उगाळणे : अगदी बारीक एमरी किंवा कार्बोरंडम पूड वापरून ही क्रिया केली जाते. यामध्ये पृष्ठाचा आकार फारसा बदलत नाही पण त्याचा खडबडीतपणा मोठ्या प्रमाणात कमी होतो. (३) उजाळा देणे : वरील क्रियांनी भिंगाच्या पृष्ठाला अपेक्षित आकार दिलेला असतो पण त्याचा पृष्ठभाग घर्षित काचेसारखा असतो म्हणजेच तो पारदर्शक नसतो. त्याला पारदर्शक करण्यासाठी त्याच्या पृष्ठावरील सूक्ष्म चरे व उंच सखल भाग मऊ पुडीने घासून सारखे करावे लागतात. या क्रियेला उजाळा देणे असे म्हणतात.

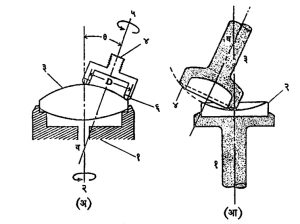
उगळण्याच्या पद्धती : हाताने उगाळण्याच्या जुन्या पद्धतीत प्रकाशीय काचेचा तुकडा डांबरासारख्या चिकट पदार्थाने एका लाकडी मुठीला चिकटवितात. उगाळण्यासाठी इष्ट त्रिज्येचे (बहिर्गोल पृष्ठासाठी अंतर्गोल व अंतर्गोल पृष्ठासाठी बहिर्गोल) लोखंडी हत्यार (आ. ९) वापरतात. हत्यारावर प्रथम जाड व नंतर क्रमाक्रमाने जास्त जास्त बारीक एमरी पूड व थोडे पाणी टाकतात आणि त्यावर मूठ हातात धरून काचेचा तुकडा उगाळून त्याला योग्य तो आकार देतात. शेवटी ओल्या फेरिक ऑक्साइडाच्या पुडीने घासून त्याला झिलई देतात. ही पद्धत मोठ्या प्रमाणावर भिंगांचे उत्पादन करण्यास सोयीची नाही. बहूत्पादनासाठी हिऱ्याची पूड लावलेले वक्रतोत्पादक यंत्र वापरतात (आ. १०). यामध्ये उदग्र अक्षाभोवती वेगाने फिरू शकणारी एक बैठक असते. तिच्यावर काचेचा इष्ट आकाराचा तुकडा चिकटवून बसवितात किंवा निर्वात यंत्रणेने तो बैठकीवर धरून ठेवण्याची व्यवस्था केलेली असते. उगाळक हत्यार पोकळ वृत्तचितीच्या (कपाच्या) आकाराचे असून त्याच्या वलयाकार टोकावर हिऱ्याची पूड चिकटवून बसविलेली असते. बैठकीच्या भ्रमण अक्षाशी ठराविक कोन (θ) केलेल्या अक्षाभोवती हे हत्यार वेगाने फिरविता येते. ‘कोणत्याही गोलाकार पृष्ठावर, त्या गोलाच्या त्रिज्येपेक्षा लहान त्रिज्या असलेले वर्तुळाकार वलय बरोबर बसू शकते’ या तत्त्वावर या यंत्राचे कार्य चालते. या यंत्राने घासून काढलेल्या पृष्ठाची त्रिज्या (r) पुढील समीकरणाने दिली जाते.

r =	D
	2 cos θ

येथे D हा उगाळणाऱ्या हत्याराचा व्यास आहे.

एका पृष्ठाची उगाळण्याची क्रिया संपल्यावर काचेचा तुकडा उलटून बसवतात व दुसरी बाजू उगाळतात. θ या कोनाचे मूल्य बदलून वेगवेगळ्या वक्रता त्रिज्यांची पृष्ठे करता येतात.

उगाळण्याचे काम चालू असताना मधून मधून अपेक्षित त्रिज्या निर्माण झाली आहे की नाही हे खास उपकरणाच्या साहाय्याने पाहून त्यानुसार उगाळण्याची क्रिया केव्हा थांबवावयाची ते ठरवावे लागते. अंतर्गोल पृष्ठाची अशी प्राथमिक परीक्षा करण्यासाठी इष्ट त्रिज्येची पत्र्याची तबकडी त्या पृष्ठात बसवून ती सर्वत्र पृष्ठाला टेकते की नाही हे पाहतात. शेवटी त्याच त्रिज्येचे बहिर्गोल पृष्ठ सर्वत्र टेकते की नाही हे पाहिले जाते. बहिर्गोल पृष्ठासाठी याचप्रमाणे पत्र्यात कापलेला अंतर्गोलाकार व अंतर्गोल पृष्ठ यांचा वापर करतात.

एकाच वेळी अनेक भिंगे उगाळणे : एकाच वेळी अनेक भिंगे उगाळल्यास उत्पादन जलद होते व निर्माण होणाऱ्या भिंगांची किंमतही बरीच कमी होते. या पद्धतीला गट पद्धत असे म्हणतात. आ. ११ मध्ये भिंगांचा असा गट एका बहिर्गोल ‘गटकारका’वर चिकटविलेला दाखविला आहे. ही सर्व रचना एका उदग्र अक्षाभोवती फिरविता येते. गटकारकावर जास्तीत जास्त समाविष्ट करता येणाऱ्या भिंगांची संख्या आकृतीतील B या कोनावर अवलंबून असते.

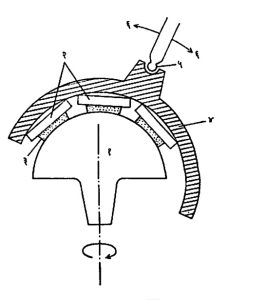
बहिर्गोल भिंगे तयार करावयाची असतील, तर या गटावर इष्ट त्रिज्येचे अंतर्गोल हत्यार असे उभारतात की, ‘गोलक खीळ-व-खोबण’ रचनेने त्याला आंदोलन गती देता येते (आ. १२). हत्याराचा अंतर्भाग व भिंगांचे वरचे पृष्ठभाग यांमध्ये एमरी पूड आणि पाणी यांचे मिश्रण असते. या पद्धतीने एकाच वेळी एकाच त्रिज्येची अनेक वक्रपृष्ठे तयार करता येतात.

उजाळा देणे : भिंगाच्या पृष्ठाला अपेक्षित वक्रता आल्यानंतर त्याला उजाळा देण्याची क्रिया हाती घेतात. या क्रियेत पृष्ठाची सर्वसामान्य वक्रता न बदलू देता त्याच्या पृष्ठावरील ओरखडे, चरे व लहानसहान उंचवटे घासून काढून पृष्ठ नितळ करावयाचे असते. उजाळा देण्यासाठी आर्यन ऑक्साइडाची किंवा सिरियम ऑक्साइडाची अगदी बारीक पूड व पाणी यांचा राळा भिंगपृष्ठावर टाकतात. त्यावरून घासणाऱ्या हत्याराच्या अंतर्भागावर बहुधा डांबराचा लेप दिलेला असतो. घासताना उत्पन्न होणाऱ्या उष्णतेमुळे हा लेप मऊ होऊन तो भिंगपृष्ठाचा आकार धारण करतो व त्यामुळे भिंगाची वक्रता आपोआपच कायम रहाते. कधीकधी घासण्यासाठी विशिष्ट प्रकारचे कापड किंवा चामडेही वापरतात. त्याचाही उपयोग वरील प्रमाणेच होतो.

अंतिम तपासणी : उजाळा दिल्यानंतर भिंगाच्या पृष्ठाची अंतिम तपासणी केली जाते. प्रथम सूक्ष्‍मदर्शकाच्या साहाय्याने पृष्ठावरील चरे व खड्डे (असल्यास) यांचे मापन करतात. समाधानकारक पृष्ठावरील चऱ्यांची जास्तीत जास्त रुंदी ८० मायक्रॉन (१ मायक्रॉन = १०^-६ मी.) व खड्ड्याचा जास्तीत जास्त व्यास ०.५० मिमी. असावा (असे पृष्ठ ८०-५०) या अंकांनी निर्देशित करतात). अती उच्च दर्जाच्या पृष्ठाचे निर्देशन २०-१० किंवा १०-५ असते. अशा तऱ्हेने पृष्ठाच्या नितळपणाची तपासणी होते.

त्यानंतर महत्त्वाची तपासणी म्हणजे पृष्ठाच्या वक्रतेची होय (वक्रता = त्रिज्येचा व्यस्तांक). ही तपासणी प्रकाशीय पद्धतीने केली जाते व सेंटिमीटरच्या एक कोट्यांश भागापर्यंत अचूकपणे करता येते. यासाठी काटेकोरपणे बनविलेली वेगवेगळ्या त्रिज्यांची काचेची मानक (प्रमाणभूत) अंतर्गोल व बहिर्गोल पृष्ठे वापरातात. बहिर्गोल पृष्ठाची परीक्षा करण्यासाठी त्याच त्रिज्येचे अंतर्गोल पृष्ठ घेऊन त्यात परीक्षा पृष्ठ घालतात. दोन्ही पृष्ठे एकमेकांना स्पर्श करतील अशी ठेवून त्यांच्यावर सोडियमाचा पिवळा प्रकाश पाडतात. पृष्ठे सर्वत्र एकमेकांना स्पर्श करीत असतील, तर एकच न्यूटन (काळे) वर्तुळ दिसेल [⟶ प्रकाशकी], नाही तर ज्या बिंदूवर ती पृष्ठे परस्परांना स्पर्श करतील त्याच्या भोवती एक किंवा अनेक न्यूटन वर्तुळे दिसतील. असे एक वर्तुळ दिसेल, तर दोहोंच्या त्रिज्यांमध्ये सोडियमाच्या तरंगलांबीच्या (= ५८९३×१०^–८ सेमी.) निम्म्याइतका फरक आहे असे व्यक्त होते. साधारणतः ५ वर्तुळे दिसली, तरी पृष्ठ समाधानकारक समजले जाते. अती उच्च दर्जाच्या पृष्ठाच्या बाबतीत एक (किंवा त्याहूनही कमी) वर्तुळ दिसते.

विनिर्देशन : (उत्पादित वस्तूच्या अपेक्षित गुणधर्मांसंबंधीचे निर्देशन). भिंगपृष्ठाचा नितळपणा, वक्रता इत्यादींच्या बाबतीत जितका जास्त काटेकोरपणा करावा तितकी भिंगाची किंमत जास्त होत जाते. अर्थात जरूरीपेक्षा जास्त काटेकोरपणा करण्यात काहीच फायदा होत नाही, हे लक्षात घेऊन भिंगाचे विनिर्देशन केले जाते. चष्म्याची भिंगे, नेत्रभिंगे यांच्या त्रिज्येची अचूकता साधारणपणे १,००० भागांत एक या सुमाराची असली तरी पुरेशी होते परंतु चांगल्या दर्जाच्या कॅमेऱ्याची भिंगे, सूक्ष्मदर्शकांची वस्तुभिंगे यांच्या बाबतीत यापेक्षा सु. १०० पट जास्त अचूकता असावी लागते.

अगोलीय पृष्ठे : दृष्टिवैषम्य, गोलीय विपथन यांसारखे प्रतिमेचे कित्येक दोष कमी करण्यासाठी अगोलीय पृष्ठांची भिंगे वापरणे हा एक चांगला उपाय आहे. प्रकाशीय व्यूहांच्या अभिकल्पासाठी (आराखड्यासाठी) आता संगणकाचा (गणक यंत्राचा) उपयोग होऊ लागल्यामुळे अगोलीय पृष्ठांचा उपयोग वाढत्या प्रमाणावर होत जाईल असे दिसते. प्रकाशीय व्यूहात सध्या तरी सममितीचा एक अक्ष असणाऱ्या अगोलीय पृष्ठांचाच मुख्यत्वेकरून वापर होतो. विवृत्तज, अन्वस्तज व अपास्तज पृष्ठे [विवृत्त, अन्वस्त व अपास्त हे वक्र अक्षाभोवती फिरवून मिळणारी पृष्ठे ⟶ भ्रमणजन्य पृष्ठे व घनाकृति] ही त्यांची उदाहरणे आहेत. त्याचप्रमाणे वृत्तजवलयी (एखादे वर्तुळ त्याच्याच प्रतलातील पण त्याला न छेदणाऱ्या अक्षाभोवती फिरविल्यास निर्माण होणाऱ्या कड्यासारख्या पृष्ठाचा भाग असलेल्या) पृष्ठांचाही वापर होतो. वृत्तजवलयी पृष्ठाच्या वक्रता त्रिज्या (सामान्यतः) दोन परस्पर लंब दिशांनी वेगळ्या असतात. दृष्टिवैषम्य या दृष्टिदोषाचे निराकरण करण्यासाठी वृत्तजवलयी भिंगे वापरली जातात.

अगोलीय पृष्ठांची भिंगे वापरण्यातील मुख्य अडचण म्हणजे अशी पृष्ठे उगाळून अचूकतेने तयार करणे हे गोलीय पृष्ठाच्या निर्मितीच्या मानाने फारच अवघड जाते. त्यामुळे अशा भिंगांचा उपयोग तूर्त तरी जेथे जास्त अचूकतेची जरूरी नसते अशा ठिकाणीच (उदा., नेत्रभिंग, पेटी कॅमेऱ्याचे भिंग इ.) केला जात आहे.

अगोलीय पृष्ठे साच्यातून दाबून काढून तयार करता येतात पण ही पद्घत मुख्यतः प्लॅस्टिकासारख्या मऊ पदार्थांची भिंगे करतानाच उपयोगी पडते. काचेची अगोलीय पृष्ठे तयार करण्यासाठी प्रथम इष्ट आकाराला अनुरूप असा एक ⇨कॅम तयार करतात. पृष्ठभाग उगाळणाऱ्या हत्याराच्या गतीचे या कॅमाने मार्गदर्शन केले जाते. पृष्ठभाग उगाळून तयार झाल्यावर त्याची चाचणी तशाच आकाराच्या परंतु उलट वक्रतेच्या पृष्ठात तो बसवून केली जाते. अशा पृष्ठाला उजाळा देताना घासणारे पृष्ठ अत्यंत लवचिक म्हणजे कापडाचे किंवा चामड्याचे वापरतात म्हणजे ते वाकून बरोबर त्या पृष्ठाचाच आकार घेते. त्यामुळे उजाळा देताना पृष्ठाच्या आकारात विशेषसा बदल होत नाही.

भिंगाचा मध्य काढणे : कोणत्याही उपकरणात भिंग बसविताना भिंगाचा अक्ष व उपकरणाचा अक्ष समानुपाती (एकाच रेषेत जुळणारे) असावे लागतात. विशेषतः भिंग-प्रणालींच्या बाबतीत सर्व घटक भिंगांचे अक्ष काटेकोरपणे समानुपाती करणे जरूर असते. यासाठी प्रथम भिंगाचा मध्य काढून घेतात मग त्याच्या कडा घासून ते बरोबर वर्तुळाकार करून घेतात.

भिंगाचा मध्य काढण्यासाठी लेथच्या अक्षाशी भिंगाचा अक्ष अंदाजाने शक्य तितका समानुपाती करून भिंग चिकट पदार्थाच्या साहाय्याने लेथवर बसवितात. मग लेथ हळूहळू फिरवून भिंगाच्या पृष्ठाभागावर परावर्तन होऊन दिसणारी एखाद्या दीप्त वस्तूची प्रतिमा पहातात. दोन्ही अक्ष समानुपाती नसल्यास ही प्रतिमाही फिरताना दिसते. लेथवरील भिंगाची स्थिती अशी बदलतात की, शेवटी ती प्रतिमा स्थिर रहावी म्हणजेच भिंगाचा आणि लेथचा अक्ष समानुपाती होतात. मग या परिस्थितीत लेथ फिरवून भिंगाच्या कडा घासून ती वर्तुळाकार करतात. आता हे भिंग त्याच त्रिजेच्या नळीत बसविले, तर भिंग व नळी यांचे अक्ष समानुपाती होतील. काही यंत्रांत एकाच वेळी ४-५ भिंगांच्या कडा अशा तऱ्हेने घासता येतात.

भिंगांच्या बैठका : निरनिराळ्या प्रकाशीय उपकरणांत बसविलेली भिंगे उपकरणाशी बरोबर समाक्ष तर असली पाहिजेतच पण त्याखेरीज त्यांची परस्परांमधील अंतरे अभिकल्पानुसार निश्चित अशीच राहणे आवश्यक असते. त्याचप्रमाणे आपल्या बैठकीत भिंग फिरून त्याची समाक्षता बिघडता कामा नये.

काही परिस्थितींत (उदा., प्रकाशक्षेपकातील) भिंगाचे तापमानातील चढ-उतारामुळे आकुंचन-प्रसरण होते व त्यासाठी पुरेसा वाव ठेवणे जरूर असते. त्याचप्रमाणे भिंग बैठकीत फार दाबून बसविल्यास त्याचे विरूपण होण्याचा धोका असतो व तोही टाळला पाहिजे.

सामान्यतः भिंगे त्यांच्या इतक्याच त्रिज्येच्या वर्तुळाकार बैठकीत बसविली जातात. तेथे ती हलू नयेत म्हणून केव्हा केव्हा चिकटपदार्थाने ती चिकटवून ठेवतात किंवा एखाद्या स्प्रिंगेने दाबून धरून ठेवतात. भिंगावर आटे पाडलेले समाक्ष कडे घट्ट बसवूनही भिंग पक्के बसविता येते. कधीकधी भिंग-बैठकीत भिंग बसविल्यावर नळीची कड सर्व बाजूंनी सारखी आत वळवून त्याखाली ते दाबून धरले जाते. (आ. १३).

भिंगे एकत्र चिकटविणे : भिंगांच्या काही रचनांत (उदा., विवर्ण भिंग-जोडी) लागोपाठची दोन भिंगे एकमेकांना चिकटवून बसवितात. यात दोन उद्देश साध्य होतात. एक तर परस्परांच्या संदर्भात त्या भिंगांच्या स्थिती न बदलता कायम जशाच्या तशाच राहतात आणि दुसरे म्हणजे त्या दोघांच्या मधील पृष्ठांवरून होणारे प्रकाशाचे (अंशतः) परावर्तन अगदी कमी होऊन प्रतिमा जास्त तेजस्वी मिळते.

भिंगे चिकटविताना एका भिंगाचे बहिर्गोल पृष्ठ दुसऱ्याच्या (समान त्रिज्येच्या) अंतर्गोल पृष्ठाला चिकटविले जाते. भिंगे एका ठराविक स्थितीतच समाक्ष रीत्या परस्परांना चिकटविली पाहिजेत, तसेच मधल्या पारदर्शक चिकट पदार्थात बुडबुडे रहाता कामा नयेत, याकरिता दक्षता घ्यावी लागते.

पूर्वी या कामासाठी कॅनडा बाल्सम [⟶ बाल्सम] नावाचा पारदर्शक पदार्थ (ओलिओरेझीन) वापरीत असत परंतु तापमान फार जास्त किंवा कमी झाले, तर हा पदार्थ अकार्यक्षम होतो. म्हणून हल्ली भिंगे चिकटविण्यासाठी एपॉक्सी किंवा मेथॅक्रिलेट प्रकारची रेझिने वापरणे अधिक पसंत करतात.

परावर्तन विरोधक विलेपण : भिंगांच्या पृष्ठापासून अंशतः परावर्तन झाल्यामुळे प्रतिमेचा तेजस्वीपणा कमी होतो. क्राउन काचेवर लंब दिशेने आपाती झालेल्या प्रकाशांपैकी ४.३% प्रकाश परावर्तित होऊन वाया जातो. चांगल्या कॅमेऱ्याच्या भिंगसमूहात असे १४ पृष्ठभाग आल्यास त्यापासून परावर्तनामुळे निम्म्याहून अधिक प्रकाश फुकट जातो. हे टाळण्यासाठी भिंगांच्या पृष्ठावर मॅग्‍नेशियम फ्ल्युओराइडाच्या किंवा झिंक सल्फाइडाच्या अगदी पातळ थराचे विलेपन करतात. निर्वातामध्ये वरीलपैकी एक द्रव्य वितळवून त्याचे बाष्प तयार करतात व हे बाष्प भिंग पृष्ठावर बसू देतात. या लेपाची जाडी (अपेक्षित) प्रकाशाच्या तरंगलांबीच्या एक चतुर्थांश इतकी सूक्ष्म असते. या थराच्या वरच्या व खालच्या पृष्ठांपासून अंशतः परावर्तन झालेले प्रकाश तरंग विनाशी व्यतिकरणामुळे (दोन तरंगमालिकांमध्ये होणाऱ्या परस्पर क्रियेमुळे) परस्परांना नष्ट करून टाकतात व त्यामुळे परावर्तित प्रकाश ऊर्जा अत्यंत कमी होते. विलेपनाची जाडी पिवळ्या प्रकाशाचे विनाशी व्यतिकरण होण्यास योग्य असल्यास या पृष्ठापासून पांढऱ्या प्रकाशापैकी तांबडा व निळा भाग बऱ्याच प्रमाणात परावर्तित होतो आणि त्यांच्या मिश्रणामुळे अशा भिंगाचे पृष्ठभाग जांभळट रंगाचे दिसतात. सर्व चांगल्या दर्जाच्या प्रकाशीय उपकरणांतील भिंगांचे पृष्ठभाग अशा तऱ्हेने विलेपित केलेले असतात.

चष्म्याची भिंगे : प्रणमनात्मक दृष्टीदोषांचे निराकरण योग्य प्रकारची भिंगे असलेले चष्मे वापरून करता येते. उदा., लघू दृष्टी हा दोष दूर करण्यासाठी ऋण व दिर्घ दृष्टी हा दोष दूर करण्यासाठी धन भिंगांचे चष्मे वापरावे लागतात [⟶ चष्मा]. त्याचप्रमाणे दृष्टिवैषम्य या दोषाचे निराकरण वृत्तजवलयी किंवा चितीय भिंगांचा चष्मा वापरून करता येते.

चष्मा हलका होण्यासाठी चष्म्याची भिंग शक्य तितकी पातळ करतात. बुबुळे फिरवून वेगवेगळ्या दिशांनी नीट पहाता यावे यासाठी चष्म्याच्या भिंगांचा डोळ्याच्या बाजूचा भाग अंतर्गोल केलेले असतो. चष्म्याची भिंगे ही कॅमेरे किंवा सूक्ष्मदर्शक यांच्या भिंगांइतकी काटेकोरपणे तयार करण्याची जरूरी नसते. त्यामुळे ती स्वस्त किंमतीत देता येतात.

ही भिंगे तयार करण्याच्या पद्धती मागे दिलेल्या पद्धतींसारख्याच आहेत. चष्म्यासाठी वृत्तजवलयी भिंगे मोठ्या प्रमाणावर लागत असल्याने त्यांच्या बहूत्पादनासाठी उगाळण्याची क्रिया करणारे एक खास यंत्र बनविण्यात आले आहे.

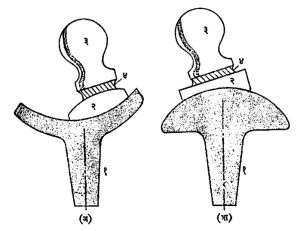
द्विकेंद्री व त्रिकेंद्री भिंगे : उतार वयात नेत्र-अनुकूलनाची (निरनिराळ्या अंतरांवरील वस्तू स्पष्टपणे दिसण्यासाठी डोळ्यातील भिंगाची बहिर्वक्रता अंतःस्थ स्‍नायूंच्या आकुंचन-प्रसरणामुळे कमीजास्त होण्याची) शक्ती कमी झाल्यामुळे जवळच्या वस्तू स्पष्ट दिसू शकत नाहीत. या दोषाला वृद्ध दृष्टी असे म्हणतात. हा दोष दीर्घ दृष्टीपेक्षा वेगळा आहे. कारण या दोषाने ग्रस्त झालेल्या व्यक्तीला योग्य शक्तीच्या धन भिंगाच्या चष्म्यातून जवळच्या वस्तू स्पष्ट दिसतात परंतु दूरच्या दिसू शकत नाहीत. इतकेच नव्हे, तर कित्येकदा दूरच्या वस्तू स्पष्ट दिसण्यासाठी ऋण भिंगाचा चष्मा वापरणे जरूर पडते. असे दोन चष्मे वापरणे त्रासदायक असल्याने बेंजामिन फ्रँक्लिन यांनी १७९४ मध्ये एकाच चष्म्याच्या चौकटीत वरच्या अर्ध्या भागात दूरचे पहाण्याचे भिंग व खालच्या अर्ध्या भागात वाचण्यास योग्य असे भिंग वापरले. अखंड काचेतील द्विकेंद्री भिंगे १९०० सालाच्या सुमारास माल्कम बेंटझन व ए. एच्. एमर्सन यांनी ब्रिटनमध्ये प्रचारात आणली. या पद्धतीत एकाच काचेवर जवळचे पहाण्यासाठी जास्त धन शक्तीचा भाग व दूरचे पहाण्यासाठी कमी धन शक्तीचा किंवा जरूर तर ऋण शक्तीचा भाग उगाळण्यात येतो.

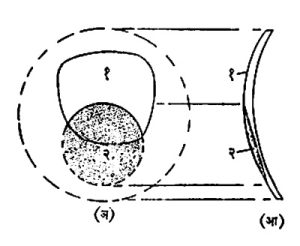
वितळजोडाच्या द्विकेंद्री भिंगाच्या शोध अमेरिकेत जे. एल्. बॉर्श यांनी १८९९ मध्ये लावला. या प्रकारात कमी प्रणमनांक असलेल्या काचेवर जास्त प्रणमनांक असलेल्या काचेचा एक तुकडा भट्टीत वितळवून जोडण्यात येतो. भिंग उगाळताना या जास्त प्रणमनांकयुक्त भागावर जवळच्या वस्तू पहाण्यासाठी जास्त धन शक्तीची वक्रता व इतर भागावर दूरच्या दृष्टीसाठी कमी शक्तीची वक्रता निर्माण केली जाते (आ. १४).

काही लोकांना अशा द्विकेंद्री भिंगाने अगदी जवळच्या व अगदी दूरच्या वस्तू नीट दिसू शकतात परंतु दरम्यानच्या वस्तू चांगल्या दिसत नाहीत. त्यांच्यासाठी त्रिकेंद्री भिंगे तयार करण्यात येतात. अशा भिंगात वेगवेगळ्या शक्तीचे तीन वेगळे विभाग असतात.

स्पर्श भिंगे : विसाव्या शतकाच्या आरंभी बुबुळाच्या स्वच्छ मंडलावर चिकटून बसणारी स्पर्श भिंगे वापरता येऊ लागली. या प्रकारच्या काचेच्या भिंगांची किंमत फारच जास्त पडते व ती सहज फुटू शकतात म्हणून हल्ली प्लॅस्टिकाचीच स्पर्श भिंगे वापरली जातात. भिंग प्रथम साच्यात ओतून तयार केले जाते. नंतर ते गरम करून व त्यावर दाब देऊन त्याला वापरणाऱ्याच्या बुबुळावर बरोबर बसेल असा आकार देण्यात येतो.

दीपगृहासाठी लागणारी भिंगे : ही भिंगे मोठी असल्यामुळे त्यांचे वजनही मोठे असते. एका अखंड भरीव काचेच्या तुकड्यातून असे भिंग तयार करणे त्याच्या वजनामुळे अशक्य प्राय होते. नेहमीच्या पद्धतीने भिंगे तयार करण्याच्या ऐवजी एकापाठोपाठ एक अशी समकेंद्री कडी तयार केल्यास भिंगाचे वजन पुष्कळच कमी करता येईल अशी युक्त १७४८ मध्ये जी. एल्. एल्. द ब्यूफाँ या फ्रेंच शास्त्रज्ञांनी सुचविली होती. ही युक्ती आ. १५ मध्ये दाखविली आहे.

या युक्तीनुसार ए. जे. फ्रेनेल यांनी १८२० मध्ये दीपगृहासाठी लागणारी व वजनात हलकी अशी भिंगे तयार केली. अशा भिंगांना फ्रेनल भिंगे म्हणतात. [⟶ दीपगृह].

अलीकडील दीपगृहाला लागणाऱ्या भिंगाचे छेद काचेच्या योग्य अशी वक्र दांड्यापासून तयार करतात व ते छेद निरनिराळे घासून त्यांना उजाळा देतात व धातूच्या चौकटीत हे छेद बसविल्यानंतर एकसंध भिंग तयार होते. साच्यात घालून तयार केलेल्या एकसंघ काचेच्या फ्रेनेल भिंगाचे बहुविध उपयोग आहेत. निरनिराळ्या प्रकारची फ्रेनेल भिंगे विविध प्रकारच्या प्लॅस्टिकांपासूनही बनविण्यात येऊ लागली आहेत. या फ्रेनेल भिंगातील कडी शतांश मिमी. इतक्या जाडीची असतात. या भिंगांचा उपयोग घर्षित काचेच्या पडद्याचा वापर करणाऱ्या रिफ्लेक्स कॅमेऱ्यातील क्षेत्र भिंगे, छोटे प्रकाशझोत क्षेपक, क्ष-किरण छायाचित्रक्षेपक, रेल्वे व रस्त्यावरील नियंत्रण दिव्यांची भिंगे, विमानतळावरील प्रदीपन इत्यादींसाठी करण्यात येतो. चंडीगढ येथील सेंट्रल सायंटिफिक इन्‍स्‍ट्रूमेंट्‍स ऑर्गनायझेन या संस्थेने प्लॅस्टिकाची फ्रेनेल भिंगे तयार करण्याचे तंत्र विकसित केलेले असून सौर ऊर्जेचे सौर विद्युत्‍ घटाच्या साहाय्याने विद्युत्‍ ऊर्जेत रूपांतर करण्यासाठी या भिंगांचा उपयोग करण्यात येणार आहे.

मोटारीच्या पुढील मोठ्या दिव्यांना बसविण्यात येणारी मोठी भिंगे फ्रेनेल भिंगाच्या जातीतील आहेत. यात समकेंद्री कडी नसतात. त्याऐवजी अनेक लहान लहान चौकोनी भाग असून त्यांची रचना अशी केलेली असते की, दिव्यातून बाहेर पडणारा प्रकाश रस्त्यावर केंद्रित करता येतो किंवा एका बाजूला वळविता येतो.

पहा : कॅमेरा; चष्मा; दूरदर्शक; प्रकाशक्षेपक; प्रकाशीय व्यूहांतील विपथन; सूक्ष्मदर्शक.

संदर्भ : 1. Jenkins, F. A.; White, H. E. Fundamentals of Optics, New York, 1976.

2. KingsIake, R. and others, Ed., Applied Optics and Optical Engineering, 7 Vols., New York, 1965-1979.

3. Smith, W. J. Modern Optical Engineering, New York, 1966.

4. Twyman, F. Prism and Lens Making : A Textbook for Glassmakers, Boston, 1952.

कर्णिक, मा. भ.; पुरोहित, वा. ल.; टोळे, मा. ग.