फलन: कवखया दोन संचामधील(उदा., व्यक्ती, वस्तू, वैज्ञानिक निरीक्षणे इत्यादींच्या समूहातील) घटकांमध्ये निरनिराळ्या पद्धतींना संगती लावता येते. ज्या वेळेस क संचातील प्रत्येक घटकाची संगती ख संचातील एका आणि एकाच घटकाशी लावली जाते तेव्हा त्या संगतीत ‘ फलन ’ म्हणतात व ते फ: क ⟶ ख असे दर्शवितात. क संचास फलनाचा प्रांत व ख संचास सहप्रांत असे संबोधण्यात येते. समजा, क्ष हा क संचातील घटक दिलेल्या संगतीने ख संचातील य या घटकाशी निगडित आहे. य ला क्ष ची प्रतिमा म्हणून ओळखतात व हा संबंध य= फ(क्ष) असा दर्शविला जातो. क संचातील सर्व घटकांच्या प्रतिमांच्या संचास फलनाची कक्षा म्हणतात. अर्थात हा संच ख संचाचा उपसंच असतो. दिलेली संगती एकास-एक असेल, तर ख संचास प्रांत मानून ख संचातील प्रत्येक घटकाशी संगत असलेला क संचातील घटक त्याची प्रतिमा मानल्यास नवे फलन मिळते. या फलनास व्यक्त फलन म्हणतात व त्याकरिता फ-१ हे चिन्ह वापरतात. फलनाची कक्षा संपूर्ण ख संच असेल, तर अशा फलनाला आच्छादक फलन म्हणतात. अन्यथा त्याला आंतर फलन म्हणतात. ख मधील प्रत्येक घटक एका आणि एकाच क- घटकाची प्रतिमा असेल, तर त्या फलनास एकास- एक फलन म्हणतात. अन्यथा फलनास अनेकास- एक फलन म्हणतात.
फलन सिद्धीकरिता वापरलेली संगती काही वेळा सूत्ररूपाने मांडता येते. समजा क आणि ख हे संख्या संच आहेत व क्ष आणि य हे त्यातील घटक य= क्ष२ असे संबंधित आहेत. या संबंधाने एक फलन मिळते व त्याची संगती सूत्ररूपात मिळते. फलन सिद्धीकरिता अशा तऱ्हेचे सूत्र पाहिजेच असे नाही. क्ष हा क संचावरील चल असेल व य हा ख संचावरील चल असेल, तर क्ष ला स्वयंचल व य ला परचल म्हणण्याची पद्धत आहे.
इतिहास: फलनाची संकल्पना १६३७ मध्ये रने देकार्त यांच्यापासून सुरू झालेली आढळते. त्यांनी सुरू केलेल्या सहनिर्देशक भूमितीमध्ये[⟶ भूमिती] वक्रावरील बिंदूचे क्ष, य हे सहनिर्देशक चल असतात. बिंदूचे वक्रावरील स्थान या दोन चलांमधील फलन संबंध दर्शविते. जी. डब्ल्यू. लायप्निट्स या गणितज्ञांनीFunktion ( फलन) हा शब्द १६९४ मध्ये रूढ केला. त्यांनी हा शब्द वक्रावरील बिंदूंशी संबंधित भुज, कोटी, स्पर्शिका, लंब इत्यादींच्या लांबीच्या संदर्भात वापरला. जे. बेर्नुली यांनी १६९८ मध्ये फलन शब्द चल व स्थिरांक यांनी तयार झालेल्या राशींकरिता वापरला. फलनाकरिता फ( क्ष) या स्वरूपाचे लेखन लेनर्ड ऑयलर यांनी १७३४ मध्ये रूढ केले. त्यांनी लिहिलेल्याIntroduction in analysin infinitorum ( १७४८) हा ग्रंथ फलन सिद्धांतावरील पहिला ग्रंथ मानता येईल. त्यानंतर जे. एल्. लाग्रांझ यांनी १७९७ मध्ये आपल्या लेखनाद्वारे फलन सिद्धांताच्या बाबतीत पुष्कळच मौलिक भर घातली. त्यांची अवकलन शास्त्राच्या[⟶ अवकलन व समाकलन] प्रक्रिया स्वयंचलांच्या श्रेढीच्या गुणधर्मावर आधारित केल्या. जे. बी. जे. फूर्ये यांच्या संशोधनानंतर फलनाकरिता⇨ फूर्ये श्रेढी चा वापर सुरू झाला. अलीकडील फलन सिद्धांताच्या विचारामध्ये ए. एल्. कोशी, जी. एफ्. बी. रीमान व के. टी. डब्ल्यू. व्हायरश्ट्रास यांनी महत्त्वाची भर घातली. विशेषतः व्हायरश्ट्रास यांनी या विषयाचे अंकगणितीकरण करून सर्व व्याख्या समीकरणे व असमा( असमानतादर्शक संबंध) यांवर आधारित केल्या. गेओर्क कँटर यांचे संचविज्ञानही प्रांत वगरे संकल्पना मांडण्याकरिता साहाय्यभूत ठरले.
काही महत्त्वाची फलने:
( १) य= अo क्ष न+ अ १ क्ष न– १+ ….. + अ न
(अo, अ १, …, अ न सत् संख्या न पूर्णांक क्ष चल).
( २)
|
य= |
अo क्ष न+ अ १ क्ष न– १+ …… + अ न |
|
बo क्ष म+ ब१ क्ष म-१+ ….. + ब म |
(अo, अ १, ….., अ न बo, ब १, …., ब म सत् संख्या म, न पूर्णांक क्ष चल).
( ३) य= अ क्ष(अ धन स्थिरांक).
( ४) य= लॉग(क्ष).
( ५) य= ज्या क्ष य= कोज्या क्ष …… वगैरे.
( ६) य= अपाज्या क्ष य= अपाकोज्या क्ष ….. वगैरे.
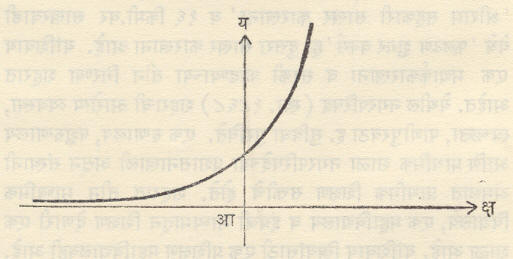
( १) मधील फलनाला ‘ बहुपदी फलन ’ म्हणतात. हे फलन सत् संख्या संचावर[⟶ संख्या] संतत व अवकलनीय असते [ ⟶ अवकलन व समाकलन].
( २) मधील फलनाला ‘ परिमेय फलन ’ म्हणतात. ज्या क्ष च्या मूल्यांना छेदाचे मूल्य शून्य होते अशी मूल्ये सोडून बाकी सर्व मूल्यांना हे फलन संतत व अवकलनीय असते.

( ३) मधील फलनाला ‘ घातीय फलन ’ म्हणतात हे फलन सत् संख्या संचावर संतत व अवकलनीय असते. याची कक्षा शून्याहून अधिक असणाऱ्या सर्व सत् संख्यांचा संच होय.
( ४) मधील फलनाचा प्रांत म्हणजे धन सत् संख्यांचा संच. हे फलन त्याच्या प्रांतातील सर्व मूल्यांना संतत व अवकलनीय असते.
( ५) मधील फलने म्हणजे नित्य वापरात असलेली त्रिकोणमितीय फलने ज्या(क्ष) व कोज्या(क्ष) सत् संख्या संचावर संतत व अवकलनीय आहेत. त्रिकोणमितीय फलने आवर्त फलने असतात. [⟶ त्रिकोणमिति].
( ६) मधील फलनांची व्याख्या पुढीलप्रमाणे करतात
अपाज्या(क्ष)= १/२(eक्ष– e-क्ष)
अपाकोज्या(क्ष)= १/२(e क्ष+ e-क्ष) वगैरे. येथेe हा स्वाभाविक लॉगरिथमाचा आधारांक असलेली संख्या आहे[ ⟶ इ].
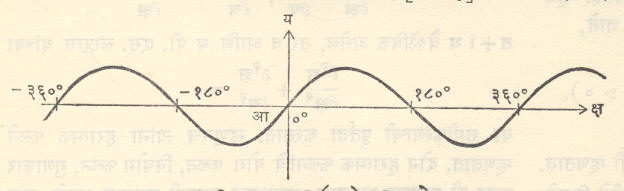
वर वर्णन केलेल्या काही फलनांचे आलेख आकृती १, २ आणि ३ मध्ये दिले आहेत.
सत् चलाची फलने: सत् चलाच्या( जो फक्त सत् संख्या मूल्ये धारण करतो अशा चलाच्या) फलनांकरिता सीमा, संततता, अवकलज, समाकल या महत्त्वाच्या संकल्पना आहेत[⟶ अवकलन व समाकलन].
फ( क्ष) हे( अ, ब) अंतरालात संतत असेल, तर त्याचे पुढील गुणधर्म लक्षणीय असतात.
( १) फ(क्ष) बंधित असते म्हणजे फ(क्ष) चे मूल्य एखाद्या स्थिरांकापेक्षा(ऊर्ध्व बंध) नेहमी कमी असते[अ थवा एखाद्या स्थिरांकापेक्षा(निम्न बंध) नेहमी जास्त असते]. ( २) फ(अ) < क< फ(ब) असेल, तर फ(क्ष) चे मूल्य एकदा तरी क बरोबर असते. ( ३) फ(क्ष) चे मूल्य एकदा तरी त्याच्या ऊर्ध्व बंधाबरोबर व एकदा तरी नि म्न बंधाबरोबर असते. (४) क्षo च्या परिसरात फ(क्ष) आणि फ(क्षo) ही मूल्ये एकाच चिन्हाची असतात. (५) फ(क्ष) एकविध(दिलेल्या अंतरालात सर्वत्र) संतत असते.
श्रेणी व⇨ श्रेढी यांमध्ये प्रत्येक पद फलन असल्यास अशा श्रेणींचा व श्रेढींचा अभ्यास हा एक महत्त्वाचा विषय आहे. त्याकरिता अभिसारिता, केवल अभिसारिता, एकविध अभिसारिता या संकल्पना वापरल्या जातात. प्रत्येक पद संतत असेल व श्रेढी एकविध अभिसारी असेल, तर त्या श्रेढीचे योग फलनही( श्रेढीतील चलांची बेरीज करून मिळणारे त्यांचे फलनही) संतत असते, तसेच प्रत्येक पद समाकलनीय असेल व श्रेढी एकविध अभिसारी असेल, तर योग फलन समाकलनीय असते.
फलन फ( क्ष) काही अटींची पूर्तता करीत असेल, तर श्रेढीच्या स्वरूपात मांडता येते. याकरिता महत्त्वाचा सिद्धांत म्हणजे ब्रुक टेलर यांचे प्रमये होय[⟶ अवकलन व समाकलन]. तसेच पी. ए. लॉरां( सदसत् चलांच्या वैश्लेषिक फलनांसाठी) व फूर्ये यांचे सिद्धांतही वापरण्यात येतात.
फलनांचे प्रकार: बंधित फलने: एखादा संख्या संच बंधित आहे किंवा नाही हे ठरविण्याची रीत: जर म हा असा स्थिरांक अस्तित्वात असेल की, क संचाच्या कोणत्याही( क्ष) घटकासाठी क्ष< म असेल, तर क संच ऊर्ध्व बंधित आहे असे म्हणतात. तसेच क्ष> म ’ ( स्थिरांक) असेल, तर क संच अधोबंधित आहे असे म्हणतात. क मधील प्रत्येक क्ष साठी । क्ष ।< म ’’ असेल, तर क संच बंधित आहे असे म्हणतात. फलनाची कक्षा एक संख्या संच असल्यामुळे फलनाकरिताही वरील संज्ञा वापरता येतात. जर क्ष च्या प्रांतातील सर्व मूल्यांना फ( क्ष) < म असेल, तर फलन ऊर्ध्व बंधित आहे असे म्हणतात. याच धर्तीवर अधोबंधित व बंधित फलनांच्या व्याख्या करतात. बंधित फलनाची उदाहरणे म्हणजे ज्या( क्ष) आणि कोज्या( क्ष) कारण । ज्या( क्ष) ।< १ आणि । कोज्या( क्ष) ।< १.
आवर्त फलने: जर फ( क्ष) असे असेल की फ( क्ष+ अ) = फ( क्ष), अ स्थिरांक, तर फ( क्ष) आवर्त फलन आहे असे म्हणतात आणि अ ला फ( क्ष) चा आवर्तनांक म्हणतात. उदा., ज्या(क्ष) व कोज्या(क्ष) यांचा आवर्तनांक २ π आहे, तर स्प(क्ष) चा आवर्तनांकπ आहे.
एकदिक् फलने: समजा फ(क्ष) चा प्रांत(अ, ब) अंतराल आहे आणि अ< क्ष ’ < क्ष ’’ < ब असताना फ(क्ष ’) < फ(क्ष ’’), तर फ(क्ष) ला वर्धमान फलन म्हणतात. तसेच अ < क्ष ’ < क्ष ’’ < ब असताना फ(क्ष ’) > फ(क्ष ’’), तर फ(क्ष) ला ऱ्हा समान फलन म्हणता त. वरील दोन्ही प्रकारच्या फलनांना एकदिक् फलने म्हणतात. कोज्या(क्ष) हे फलन(o, π ) या अंतरालात ऱ्हा समान आहे.
एकदिक् फलनाचा एक गुणधर्म असा की, जर फलन( अ, ब) अंतरालात एकदिक् आणि अवकलनीय असेल, तर त्याचा अवकलज एकाच चिन्हाचा असतो. वर्धमान फलनाचा अवकलज धन व ऱ्हासमान फलनाचा ऋण असतो. याचा व्यत्यासही सत्य आहे. एकदिक् फलनाचा आणखी एक गुणधर्म म्हणजे य = फ( क्ष) एकदिक् असेल, तर त्यापासून फ– १( य) हे व्यस्त फलनही मिळू शकते.
बंधित फेरबदलाची फलने: समजा फ(क्ष) असे आहे की,
अ= क्षo < क्ष १< क्ष २< . . . . . . < क्षन= ब
हे(अ, ब) अंतरालाचे कोणतेही विभाजन घेतल्यास
|
न |
| फ(क्षर) – फ(क्षर-१)| < क, (क स्थिरांक) |
|
∑ |
|
|
र= १ |
तर फ(क्ष) ला बंधित फेरबदलाचे फलन म्हणतात. बंधित फेरबदलाचे फलन दोन एकदिक् फलनांच्या फरकाबरोबर असल्याचे दाखविता येते व या चा व्यत्यासही सत्य आहे. बंधित फेरबदलाचे फलन रीमान यांच्या व्याख्येप्रमाणे समाकलनीय असते[⟶ अवकलन व समाकलन].
बैजिक फलने: जी फलने बैजिक समीकरणापासून सिद्ध होतात, त्यांना बैजिक फलने म्हणतात. यांमध्ये बहुपदी व परिमेय फलने यांचा समावेश होतो. याची उदाहरणे म्हणजे ‘ काही महत्त्वाची फलने ’ या उपशीर्षकाखालील( १) व( २) फलने होत.
बीजातील फलने: जी फलने बैजिक नाहीत त्यांना बीजातील फलने म्हणतात. यांमध्ये घातीय, लॉगरिथमीय, त्रिकोणमितीय वगैरे फलनांचा समावेश होतो.
अंकगणितीय फलने: पूर्णांक संचावरील फलनांना अंकगणितीय फलने म्हणतात. याची उदाहरणे पुढीलप्रमाणे: न या पूर्णांकाच्या अविभाज्य गुणकांची( अवयवांची) संख्या, न च्या धन भाजकांची संख्या, न च्या विभाजनाचे प्रकार, ऑयलर फलन, ⇨ बेर्नुली संख्या वगैरे.
काही विशिष्ट फलने: काही फलनांची व्याख्या श्रेढीच्या रूपात दिलेली असते. उदा., पी. जी. एल्. डीरिक्ले यांचे फलन
|
∞ |
अन |
|
∑ |
नक्ष |
|
न = १ |
या श्रेढीने मिळते. रीमान यांचे झीटा फलन
|
∞ |
१ |
|
ζ (स)= ∑ |
नस |
|
न = १ |
हे एक डीरिक्ले फलनाचे उदाहरण आहे. गॅमा फलनाची व्याख्या पुढील समीकरणाने दिली जाते
|
∞ |
|
Γ (न) = |
|
0 |
याला ऑयलर यांचे दुसऱ्या क्रमांकाचे समाकल फलन असेही म्हणतात. बीटा फलनाची व्याख्या पुढील समीकरणाने दिली जाते,
|
१ |
|
B (म, न) = |
|
0 |
याला ऑयलर यांचे प्रथम क्रमाकांचे समाकल फलन असेही म्हणतात.
एफ्. डब्ल्यू. बेसेल यांचे फलनJ प(क्ष) हे खालील श्रेढीने मिळते,
.png)
गॅमा व बीटा फलनांचे काही गुणधर्म ‘ अवकलन व समाकलन ’ या नोंदीत(‘काही महत्त्वाचे समाकल ’ या उपशीर्षकाखाली) दिलेले आहेत. गॅमा आणि बीटा फलने सांख्यिकीतील(संख्याशास्त्रातील) ⇨ वंटन सिद्धांता त तसेच गणितीय विश्लेषणात उपयुक्त आहेत. लझांद्र व बेसेल फलने गणितीय भौतिकीय विशेष उपयुक्त आहेत. लझांद्र फलने⇨ वर्चस् विद्धांत, विद्युत् स्थितिकी( बहुशः स्थिर स्थितीत असणाऱ्या विद्युत् भारांसंबंधीचे शास्त्र), ⇨गोलीय हरात्मक यांतील प्रश्नांत येतात. बेसेल फलने पटलांची कंपने, उष्णता संवहन, विद्युत् चुंबकीय तरंगांचे⇨ समाक्ष केबल, ⇨ तरंग मार्गदर्शक इत्यादींतील प्रसारण, गोलीय हरात्मके इत्यादीसंबंधीच्या प्रश्नांत येतात.
सदसत् चलाची फलने: स्वयंचलाचा प्रांत सदसत् संख्या संच[⟶ संख्या] असेल, तर फलन सदसत् चलाचे फलन होईल. या फलनाची मूल्ये सत् संख्या किंवा सदसत् संख्या असू शकतील म्हणजेच या फलनाची कक्षा सदसत् संख्या संचाचा उपसंच असेल. समजा द = त+ i थ हे र = क्ष + i य चे फलन आहे. त हा सत् भाग क्ष आणिय चे फलन होईल व तसेच थ हा असत् भागही क्ष आणि य चे फलन होईल.
सदसत् फलनाकरिता सीमा, संततता व अवकलनीयता यांच्या व्याख्या सत् चलाच्या सीमा, संततता व अवकलनीयता यांच्या धर्तीवरच केल्या जातात. ड प्रांतात फलन द = फ( र) निश्चित केले असेल व त्या प्रांतातील प्रत्येक बिंदूशी फ( र) चा अवकलज निश्चित होत असेल, तर द ला वैश्लेषित फलन म्हणतात. ई जे. बी. गूर्सा यांनी असे सिद्ध केले की, द = फ ( र) = त + iथ वैश्लेषिक असण्याकरिता त आणि थ या फलनाचे प्रथम आंशिक अवकलज संतत असले पाहिजेत व त्यांनी कोशी- रीमान समीकरणांची पूर्तता केली पाहिजे. ती समीकरणे अशी
|
δ त |
= |
δ थ |
, |
δ त |
= – |
δ थ |
|
δ क्ष |
δ य |
δ य |
δ क्ष |
त+ i थ वैश्लेषिक असेल, तर त आणि थ पी. एस्. लाप्लास यांच्या
|
δ२झ |
+ |
δ२झ |
= 0 |
|
δक्ष२ |
δय२ |
या समीकरणाची पूर्तता करतात. म्हणूनच त्यांना हरात्मक फलने म्हणतात. दोन हरात्मक फलनांचे योग फलन, वियोग फलन, गुणाकार फलन ही हरात्मक असतात. भागाकार फलनही हरात्मक असते मात्र छेदातील फलन ड प्रांतात कोठेही शून्य होता कामा नये.
 वैश्लेषिक फलनांचे समाकल: सदसत् फलनाच्या समाकलाची व्याख्या सत् फलनांच्या समाकलाच्या धर्तीवरच केली जाते. मात्र सदसत् फलनाच्या बाबतीत समाकलाकरिता एखादा नियमित वक्र वापरला जातो.
वैश्लेषिक फलनांचे समाकल: सदसत् फलनाच्या समाकलाची व्याख्या सत् फलनांच्या समाकलाच्या धर्तीवरच केली जाते. मात्र सदसत् फलनाच्या बाबतीत समाकलाकरिता एखादा नियमित वक्र वापरला जातो.
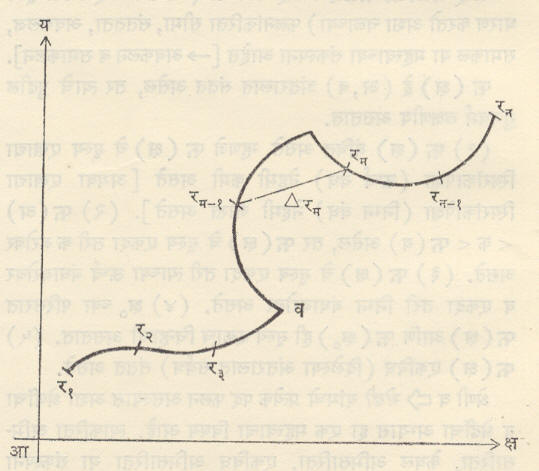
समजा व हा एक नियमित वक्र आहे(आ. ४), तर
र १, र २, . . . . . . . .., र न हे वक्रावरील कोणतेही बिंदू आहेत आणिΔ रम=रम – रम-1. न अशा त ऱ्हेने अनंताप्रत जातो की, त्याच वेळी सर्वांत मोठा । रम – रम– १→o. या समाकलाला वक्रानुसारी समाकल म्हणता त. ड प्रांतात फ(र) वैश्लेषिक असेल, तर र१ आणि र२ या बिंदूंना जोडणाऱ्या कोणत्याही नियमित वक्रावर फ(र) चा समाकल तोच असतो. हीच गोष्ट कोशी यांच्या समाकल प्रमेयाने निराळ्या तऱ्हे ने मांडलेली आहे.
कोशी यांचे समाकल प्रमेय: फ( र) हे फलन व या बंद वक्रावर आणि त्याच्या अंतर्भागात एकमूल्यी व वैश्लेषिक असेल, तर
याचे व्यस्त प्रमेयही(ई. मोरेरा यांचे प्रमेय) सत्य आहे.
रo हा बिंदू ड प्रांता असेल, तर फ (रo) करिता कोशी यांनी पुढील समाकल सूत्र दिले.
फ(र) करिता पुढील घात श्रेढी मांडता येते.
|
फ(र) = |
∞ |
कन (र-र0)न |
|
∑ |
||
|
न=० |
या ठिकाणी कन गुणक पुढील सूत्राने मिळतात.
अर्थात येथे व हा बंद वक्र असून त्यात रo चा अंतर्भाव आहे आणि त्यांच्या अंतर्भागात फ(र) वैश्लेषिक आहे. फ(र) च्या या विस्तारालाच टेलर श्रेढी म्हणतात.
फलन जर प १< र – रo < प २ सारख्या वलयाकार प्रांतात वैश्लेषित असेल, तर टेलर श्रेढीचा उपयोग होत नाही. अशा वेळी लॉरां यांच्या प्रमेयाचा उपयोग करून विस्तार लिहावा लागतो. तो पुढीलप्रमाणे:
या ठिकाणी
व हा । र- रo।= प १ आणि । र- रo ।= प २ या दोन वर्तुळांमध्ये असणारा एक बंद वक्र आहे.
वैश्लेषिक फलनाच्या एकाकी विसंगती: रo बिंदूच्या परिसरातील रo व्यतिरिक्त सर्व बिंदूपाशी फ( र) वैश्लेषित असेल, तर रo, ला फ( र) ची एकाकी विसंगती म्हणतात. फ( र) ची लॉरां विस्तार श्रेढी
|
फ(र) = |
∞ |
अन (र-र०)न |
|
∑ |
||
|
-∞ |
मांडली, तर या विस्ताराच्या स्वरूपावरून विसंगतींचे वर्गीकरण पुढीलप्रमाणे करता येते: ( १) विस्तारात(र- रo) च्या ऋण घातांची पदे नसतील, तर रo ला अपनेय(निराकरण करण्याजोगी) विसंगती म्हणतात( २) विस्तारात ऋण घातांची सांत पदे असतील व सर्वांत मोठा ऋण घात न असेल, तर रo ला ‘ न ’ व्या घाताचा ध्रुवबिंदू म्हणतात. ( ३) विस्तारात ऋण घाताची पदे अनंत असतील, तर रo ला अनिवार्य विसंगती म्हणतात. उदा.,
|
e१/र = १ + |
१ |
+ |
१ |
. |
१ |
+ . . . . . |
|
र |
२! |
२2 |
या फलनाची र= o या ठिकाणी अनिवार्य विसंगती आहे.
अवशेष: रo या ठिकाणी फ(र) ची एकाकी विसंगती असेल, तर
याला फ(र) चा रo या ठिकाणचा अवशेष म्हणतात. रo हा अनंत बिंदू असेल, तर अवशेष
येथे समाकल उलट दिशेने घेतला जातो.
कोशी यांनी अवशेषाविषयी एक मूलभूत प्रमेय मांडले असून ते पुढीलप्रमाणे आहे: फ( र) हे फलन व या बंद आणि नियमित वक्रावर आणि त्याच्या अंतर्भागात, ज्यांची संख्या सांत( न) आहे अशा ध्रुवबिंदूखेरीज, संतत असल्यास,
अनुरू पी चित्रण: समजा द= फ(र) वैश्लेषित फलन आहे व फ(र) हे ड प्रांतात कोठेही शून्य नाही. र च्या प्रत्येक मूल्याला द चे एक संगत मूल्य मिळते आणि र व द प्रतलांतील बिंदूंची संगती लावता येते. यामुळे ड प्रांताचे द प्रतलातील एका प्रांतामध्ये चित्रण होते. हे चित्रण समकोण व अभिदिशा संरक्षक असते म्हणजे θ या कोनात एकमेकांना छेदणाऱ्या दोन वक्रांचे चित्रण केले, तर चित्रणातील वक्रांमधील कोन तितकाच(0) राहतो व कोनाची दिशाही कायम राहते. यालाच अनुरूपी चित्रण म्हणतात. उदा.,
|
द = eiα |
(र-क) |
|
(र-कॅ) |
या फलनाने असत् र ≥ ० या अर्धप्रतलाचे । द । ≤ १ या वर्तुळात अनुरूपी चित्रण होते(येथे α सत् असून क ही क ची असत् संयुग्मी संख्या आहे).
समग्र फलन: जे फलन संपू र्ण र- प्रतलात वैश्लेषित असते त्याला समग्र फलन म्हणतात. अशा फलनांना विसंगती असलीच, तर ती फक्त अनंत बिंदूपाशीच असते. बहुपदी फलने समग्र फलनांचाच एक प्रकार आहेत. अनंत बिंदूपाशी असणारी एकमेव विसंगती ध्रुवबिंदू असते.
घातीय फलने: exp (र) या घातीय फलनाची व्याख्या पुढील श्रेढीने करतात.
|
exp (र) = १ + |
∞ |
|
|
∑ |
र न |
|
|
न=१ |
न! |
या श्रेढीची अभिसारण त्रिज्या अनंत आहे. exp (र) · exp (र ’) = exp (र+र ’) हे दाखविता येते. या योग प्रमेयाची घातांक नियमाशी असलेली समरूपता लक्षात घेऊनexp (र) च्या ऐवजीeर असे लिहितात.
त्रिकोणमितीय फलने: सदसत् चलाची त्रिकाणमितीय फलने पुढील श्रेढीने निश्चित करतात.
|
ज्या (र) = |
∞ |
|
|
∑ |
(-१)न र२न+१ |
|
|
न=० |
(२ न+१)! |
|
कोज्या (र) = |
∞ |
|
|
∑ |
(-१)न र२न |
|
|
न=० |
(२ न)! |
घातीय फलनाचा वापर करून ज्या(र) आणि कोज्या(र) अशीही मांडता येतील.
|
ज्या (र) = |
eIर – e-Iर |
, कोज्या (र) = |
eIर + e-Iर |
|
२ i |
२ |
र सदसत् असताना त्रिकोणमितीय नित्य समीकरणे सत्य असतात, हे दाखविता येते.
अपास्तीय फलने: ही फलने पुढील व्याख्यांनी देतात:
अपाज्या( र) = १/२(e र – e– र), अपाकोज्या( र) = १/२(e र – e– र) अर्थात येथेe र चा अर्थexp ( र) असा घ्यावयाचा.
लॉगरिथमीय फलने: घातीय फलनाचे व्यस्त फलन म्हणजे लॉगरिथमीय फलन होय. र सदसत् असेल, तर लॉग( र) बहुमूल्यी फलन असते आणि लॉग( र) = लॉग( । र ।) + i को ( र). को( र) चे प्रमुख मूल्य घेऊन लॉग( र) चे जे मूल्य मिळते त्याला प्रमुख मूल्य म्हणतात. [। र । हे र चे केवल मूल्य व को(र) हो कोनांक आहे ⟶ संख्या].
द्वि– आवर्त फलने: वर आवर्त फलनाची व्याख्या दिलेली आहे. जर फ( र) चे दोन प्रमुख आवर्तनांक असतील आणि त्या दोन आवर्तनांकांचे गुणोत्तर तस् नसेल, तर फ( र) ला द्वि- आवर्त फलन म्हणतात. या प्रकारचे प्रसिद्ध फलन म्हणजे व्हायरश्ट्रास यांचे द्वि- आवर्त फलनp ( र). के. जी. जे. याकोबी यांनी असे दाखवून दिले की, द्वि- आवर्त फलनाच्या दोन प्रमुख गुणोत्तर सत् संख्या असू शकत नाहीत, तसेच दोनांपेक्षा जास्त स्वतंत्र आवर्त असलेले फलनही असू शकत नाही. p ( र) हे फलन पुढे दिलेल्या द्वि- श्रेढीमध्ये मांडता येते.
|
p (र) = |
१ |
+ ∑ |
{ |
१ |
– |
१ |
} |
|
र२ |
म, न |
(र-Ω म,न)२ |
(Ω म,न)२ |
येथेΩ म,१ न= २ म ω १+ २न ω २ असून २ ω १ व २ ω २ हे या फलनाचे दोन आवर्तनांक आहेत.
p (र) चे योग सूत्र पुढीलप्रमाणे आहे:
|
p(र+स) = |
१ |
{ |
p'(र) – p'(स) |
}२ – p(र) – p(स). |
|
४ |
p(र) – p(स) |
अनेकचल फलने : काही वेळा एका परचलाचे मूल्य दोन किंवा अधिक स्वयंचलांशी निगडित असते. जसे य= π क्ष२र या सूत्राने क्ष त्रिज्या आणि र उंची असणाऱ्या दंडगोलाचे घनफळ(य) मिळते. येथे य परचलाचे मूल्य क्ष आणि र दोन स्वयंचलांवर अवलंबून आहे. याचत ऱ्हेनेयपरचलक्ष१, क्ष२, . ……… , क्षनयानस्वयंचलांशीनिगडितअसेल, तरएकनचलांचेफलनसिद्धहोईल. हाफलनसंबंधपुढीलप्रमाणेदर्शवितायेईल:
य= फ( क्ष१, क्ष२, …….., क्ष न)
या फलनाची संततता पुढीलप्रमाणे निश्चित करतात.
जर[( क्ष१– क्ष१’)२ + ( क्ष२ – क्ष२’)२ + …..] १/ २< δ असताना । फ( क्ष१, क्ष२, ….., क्षन) – फ( क्ष१ ’, क्ष२’, ……, क्षन ’) ।< ε तर फ हे फलन( क्ष१’, क्ष२’, ……, क्षन ’) या बिंदूपाशी संतत आ हे असे म्हणतात. बहुचल फलनामध्ये एक सोडून बाकी सर्व चल स्थिर मानले, तर त्या फलनाचा जो अवकलज मिळतो त्याला आंशिक अवकलज म्हणतात. र= फ(क्ष, य) मध्ये य स्थिर मानल्यास र चा क्ष सापेक्ष आंशिक अवकलज मिळतो व तो δर/δक्ष असा दर्शवितात.
पूर्ण अवकल : समजा र= फ(क्ष,य). जर ∆ र= फ(क्ष+ ∆ क्ष, य+ ∆ य) – फ(क्ष, य) हा बदल क∆ क्ष+ ख∆ य+p (∆ क्ष, ∆ य → o, तरp → o) असा मांडता येत असेल, तर र अवकलनीय आहे असे म्हणतात व क∆ क्ष+ ख∆ य या मुख्य भागाला र चा पूर्ण अवकल म्हणतात. तोd र ने दर्शविल्यास असे दाखविता येते.
अनेकचल फलनांविषयीचे समघात फलनांचे ऑयलर प्रमेय प्रसिद्ध आहे[⟶ अवकलन व समाकलन].
अनेकचल फलनाची महत्तम आणि लघुत्तम मूल्ये शोधण्याकरिता लाग्रांझ यांची अनिश्चित गुणकांची रीत उपयोगी पडते.
सदसत् अनेकचल फलने: सत् चलांच्या अनेकचल फलनाप्रमाणेच सदसत् चलांच्या अनेकचल फलनाची संकल्पना मांडता येते. सदसत् संख्यांचा संचC ने दर्शवितात. अर्थातCXCXC ….. (प गुणक) हा प-मितीय अवकाश होईल. तोCप ने दर्शवितात. र= (र १, र २, ….. , रप) हा या अवकाशातील एक बिंदू होईल. फ(र) र ’ च्या परिसरात
अशा अभिसारी घात श्रेढीच्या स्वरूपात मांडता येत असेल, तर फ(र) ला वैश्लेषित फलन म्हणतात. या फलनाकरिता कोशी-रीमान समीकरणे पुढीलप्रमाणे होती ल :
सदसत् प- अवकाश हे खुल्या सदसत् समुच्चयाचे एक साधे उदाहरण आहे. यापासून एक सुटसुटीत सदसत् समुच्चय बनविता येतो. त्याला सदसत् प्रक्षेपीय प- अवकाश म्हणतात. बहुचल फलनांच्या प्रगत अभ्यासात पेंडी[ आबेलीय गटांची, वलयांची वगैरे ⟶ बीजगणित, अमूर्त], सदसत् रेषा जुडगा, सदसत् सदिश जुडगा या संकल्पनांचा वापर केला जातो. पी. कुसीन यांनी व्हायरश्ट्रास व एम्. जी. मिट्टाग- लफ्लर यांच्या प्रमेयांचा प- अवकाशात विस्तार करून दोन समस्या मांडल्या. त्या के. ओका या गणितज्ञांनी सोडविल्या. ओका यांनी पूर्णरूपी प्रांतांचा विचार केला आहे. न-अवकाशातील पूर्णरूपी प्रांतांचे सत् अवकाशातील बहिर्वक्र प्रांताशी सादृश्य आहे. के. कोडायरा व डी.सी. स्पेन्सर यांनी सुटसुटीत सदसत् वैश्लेषित समुच्ययांच्या विरूपणाने विवरण केले आहे. सी.एल्. सिगेल यांनी उगत्मरूपी फलनांचे विवरण केले आहे.
सदिश फलाने: हा सदिश( परिणाम व महत्ता असलेली राशी) च या अदिश चलावरून निश्चित होत असेल, तर
हे च चे सदिश फलन होते. गतिमान बिंदूचा स्थान सदिश, वेग सदिश, प्रवेग सदिश ही सर्व सदिश फलनाची उदाहरणे आहेत.
चा अवकलज पुढीलप्रमाणे मिळतो.
|
d |
= |
सीमा |
|
|
d च |
Δ च⟶ ० |
Δ च |
सदिश एकापेक्षा अधिक चलांवर अवलंबून असेल, तर अनेकचल फलनाप्रमाणेच आंशिक अवकलज मिळविता येतात. रीमान समाकल पद्धतीने प्रदिश फलनाप्रमाणेच सदिश फलनाकरिताही रेखा, पृष्ठ व घन समाकलाच्या व्याख्या देतात येतात. [⟶ सदिश].
गट सिद्धांत: गट सिद्धांतातील समरूपण, सामियरूपण, आत्मरूपण ही फलनाचीच उदाहरणे आहेत. कारण या सर्व रूपांतरणांमध्ये दोन संचांतील घटकांमध्ये एकास एक संगती लावली जाते. [⟶ गट सिद्धांत].
अमूर्त फलन सिद्धांत: ⇨ चलनकलनशास्त्रामध्ये ज्या फलनांचा विचार केला जातो ती समाकल असतात.
जसे ∫ य √(क्ष’२ + य’२) dय.
याचे मूल्य क्ष = फ १(ट), य फ २(ट) अशा वक्राच्या आकारावर अवलंबून असते. चलनकलनशास्त्रापासून प्रेरणा घेऊन अशा फलनांचा विचार सुरू झाला की, फलनाचा प्रांत व कक्षा ही दोन्ही वर्णनात्मक गुणविशेषावर अवलंबून ठेवण्यात येऊ लागली. या अमूर्त संकल्पनांचा उपयोग नंतर⇨ पुंजयामिकी व⇨ प्राक्षेपिकी या विषयांत करण्यात येऊ लागला.
पहा: अवकलन व समाकलन विश्लेषण, गणितीय.
संदर्भ: 1 . Ahlfors, L.V. Complex Analysis, New York, 1953 .
2 . Boas, R.P. A. Primer of Real Functions, New York, 1960 .
3 . Copson, E.T. An Introduction to the Theory of a Complex Variable, London, 1961.
4 . Graves, L.M. The Theory of Functions of Real Variables, New York, 1956.
5 . Hobson, E.W. The Theory of Functions of a Real Varibale and the Theory of Fourier Series, 2 Vols., New York, 1957.
6 . Knopp, K. Trans. Bagemihl, F.Theory of Functions, 2 Parts, New York, 1945.
7. Landau, E. G. H. Trans. Streinhardt, F. Foundations of Analysis, New York, 1951.
8. Titchmarsh, E. c. The Theory of Functions, London, 1962.
पटवर्धन, ग. कृ. आगाशे, क. म. क, स. ज.
“