प्रस्थ, सामान्य : (सामान्य घनाकृती). सामान्य प्रस्थांचे अनेक प्रकार आहेत. प्रस्थाच्या अंतर्भागातील प्रत्येक बिंदू प्रस्थाचा भाग होतो. तसाच दर्शनी पृष्ठावरील बिंदूदेखील प्रस्थाचाच भाग असतो. दर्शनी पृष्ठ म्हणजेच मुखपृष्ठ अथवा पृष्ठक वा फलक होय (कोणत्याही प्रस्थाला अशा प्रकारे एक किंवा अनेक पृष्ठके वा फलक असतात). उदा., गोलाचे बाहेरील आवरण एक सलग पृष्ठ असते म्हणजे गोलाला एकच पृष्ठक असते. चौकोनी ठोकळ्यास सहा पृष्ठके असतात व त्याचे प्रत्येक पृष्ठक एका प्रतलातील चौकोनाने तयार झालेले असते. शंकूला दोन पृष्ठके असतात. एक वर्तुळाकार तळ व दुसरे त्याचे वक्रपृष्ठ. यावरून प्रत्येक प्रस्थाला एक किंवा अनेक पृष्ठके असतात व ही पृष्ठके प्रस्थाच्या मर्यादा ठरवितात, हे दिसून येईल. प्रस्थाची व्याख्या आणखी विशद करण्यासाठी ‘प्रस्थ म्हणजे भूमितीय अवकाशाचा बंधित सलग सांत भाग’ असे म्हणता येईल. प्रस्थ कोणत्या पदार्थाचा बनला आहे हा प्रश्न भूमितिशास्त्रांत गौणच मानला जातो. बाटलीहवेने भरलेली असो, पाण्याने भरलेली असो किंवा वाळूने भरलेली असो, गणिताच्या भाषेत तो एक भूमितीय अवकाशाचा भाग म्हणूनच त्या प्रस्थांचा विचार करण्यात येतो. लाकडी ठोकळा अगर तेवढाच लोखंडाचा ठोकळा गणितीय दृष्टीने केवळ अवकाशाचा भाग आहे असे, म्हटले तरी चालेल. त्या ठोकळ्याच्या प्रत्येक कणाच्या भौतिक गुणधर्मांवरून आपण त्याला लाकडाचा किंवा लोखंडाचा ठोकळा म्हणतो. आधुनिक गणिताच्या भाषेत प्रस्थाची व्याख्या पुढीलप्रमाणे देता येईल : ‘प्रस्थ म्हणजे अवकाशातील काही जागा व्यापणारा सलग बिंदूंचा बंधित संच होय’.
बैजिक भूमितीत प्रस्थाच्या पृष्ठकाचे समीकरण (वा पृष्ठकांची समीकरणे) मिळवितात. या समीकरणाने (अथवा समीकरणांनी) दिलेल्या पृष्ठास प्रस्थाच्या नावाने संबोधितात. उदा., गोलाचे समीकरण क्ष२ + य२ + झ२ = अ२ या समीकरणाची पूर्तता फक्त गोलावरील बिंदूंचे सहनिर्देशकच करतात [⟶ भूमिति] गोलाच्या अंतर्भागातील बिंदूंचे सहनिर्देशक करीत नाहीत. याकरिता गोल या प्रस्थाचे जास्त काटेकोरपणे निर्देशन पुढीलप्रमाणे करावयास हवे. क्ष२ + य२ + झ२ < अ२. क्ष = ± क, य = ± ख, झ = ±ग ही चौकोनी ठोकळ्याच्या पृष्ठकाची समीकरणे होत. चौकोनी ठोकळा या प्रस्थाचे वर्णन पुढील सूत्रांनी करता येईल. । क्ष । ≤ क, । य । ≤ ख, । झ । < ग. प्रस्थाच्या पृष्ठकांची संख्या, त्यांचे आकार किंवा प्रस्थाचा जात्य छेद (प्रस्थाच्या पृष्ठकांना लंब असलेल्या प्रतलाने घेतलेला प्रतलीय छेद) यांवरून प्रस्थाची जात ठरविली जाते व त्याप्रमाणे त्यास नामाभिधान देण्यात आले आहे. गणितामध्ये विचारात घेण्यात येणाऱ्या प्रस्थांचा पुढील विवेचनांत परिचय करून देण्यात आला आहे.
प्रचिन : (प्रिझम). आ. १ मध्ये दर्शविल्याप्रमाणे कखगघ…… ही प्रतलीय बहुभुजाकृती घेऊन या प्रतलात नसणाऱ्या ल लांबीच्या 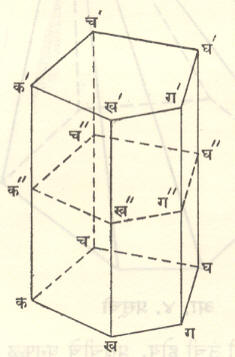 रेषेचे एक टोक या आकृतीच्या कोणत्याही बाजूवर ठेवून ही रेषा स्वतःशी समांतर ठेवून या बहुभुजाकृतीवरून फिरविल्यास या रेषेचे दुसरे टोक क´खʹगʹघʹ.… ही दुसरी प्रतलीय बहुभुजाकृती रेखाटील. या दोन बहुभुजाकृती व फिरणारी रेषा यांनी
रेषेचे एक टोक या आकृतीच्या कोणत्याही बाजूवर ठेवून ही रेषा स्वतःशी समांतर ठेवून या बहुभुजाकृतीवरून फिरविल्यास या रेषेचे दुसरे टोक क´खʹगʹघʹ.… ही दुसरी प्रतलीय बहुभुजाकृती रेखाटील. या दोन बहुभुजाकृती व फिरणारी रेषा यांनी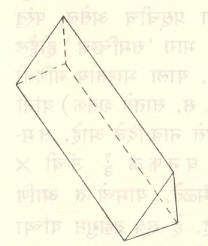
बंधित होणारा प्रस्थ म्हणजे प्रचिन होय. याची दोन पृष्ठके कखग… आणि कʹखʹगʹ... या बहुभुजाकृती एकरूप असून दोन समांतर प्रतलांत असतील तर इतर पृष्ठके समांतरभुज चौकोन असतील आणि ल रेषा कखग … या प्रतलास लंब असेल, तर त्या प्रचिनाला जात्य किंवा लंब प्रचिन म्हणतात व ती लंब नसल्यास तिर्यक् प्रचिन म्हणतात. बहुभुजाकृती सुसम (सर्व भुजा सारख्या लांबीच्या) असेल, तर सुसम प्रचिन म्हणतात. बहुभुजाकृती त्रिकोण असल्यास त्रिकोणी प्रचिन (आ. २), चौकोन असल्यास चौकोनी प्रचिन इ. नावे रूढ आहेत. समांतरभुज चौकोन असल्यास समांतरभुज प्रचिन हेही नाव रूढ आहे. हा समांतरभुज चौकोन आयत असून ल ही रेषा त्याला लंब असेल, तर त्या प्रस्थाला ‘घनकल्प’ म्हणतात. घन (षट्फलक) हा घनकल्पाचाच विशेष प्रकार आहे. यामध्ये प्रत्येक पृष्ठक चौरस असते.
चिती : प्रचिनामध्ये कखग… या बहुभुजाकृतीऐवजी एखादा प्रतलीय वक्र घेतला, तर तयार होणाऱ्या प्रस्थाला चिती म्हणतात. अर्थात ल रेषा प्रतलाला लंब असल्यास जात्य किंवा लंब चिती अन्यथा तिर्यक् चिती ही नामाभिधाने रूढ आहेत. या प्रतलीय वक्रास ‘नियत वक्र’ म्हणतात. लंब चितीचा नियत वक्र वर्तुळ
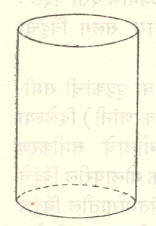 असल्यास त्या प्रस्थाला दंडगोल (आ. ३) म्हणतात. नियत वक्र विवृत्त (दीर्घवर्तुळ) असल्यास प्रस्थाला विवृत्तीय चिती म्हणतात. वरील व्याख्येवरून चितीला तीन पृष्ठके असतात, हे उघड आहे. ती म्हणजे दोन समांतर प्रतलीय वक्रांनी तयार झालेले तळ व ल या रेषेने तयार झालेले वक्रपृष्ठ. ल या रेषेला जनक रेषा म्हणतात. समांतर प्रतलांतील पृष्ठांना कधीकधी तळ किंवा पृष्ठके असेही म्हणतात. चितीचे घनफळ म्हणजे तळाचे क्षेत्रफळ व चितीची उंची यांचा गुणाकर होय.
असल्यास त्या प्रस्थाला दंडगोल (आ. ३) म्हणतात. नियत वक्र विवृत्त (दीर्घवर्तुळ) असल्यास प्रस्थाला विवृत्तीय चिती म्हणतात. वरील व्याख्येवरून चितीला तीन पृष्ठके असतात, हे उघड आहे. ती म्हणजे दोन समांतर प्रतलीय वक्रांनी तयार झालेले तळ व ल या रेषेने तयार झालेले वक्रपृष्ठ. ल या रेषेला जनक रेषा म्हणतात. समांतर प्रतलांतील पृष्ठांना कधीकधी तळ किंवा पृष्ठके असेही म्हणतात. चितीचे घनफळ म्हणजे तळाचे क्षेत्रफळ व चितीची उंची यांचा गुणाकर होय.
प्रसूची : (पिरॅमिड). आ. ४ मध्ये दर्शविल्याप्रमाणे एक कोणतीही प्रतलीय बहुभुजाकृती घेऊन त्या प्रतलाबाहेरील एक बिंदू बहुभुजाकृतीच्या प्रत्येक शिरोबिंदूस जोडल्यास तयार होणाऱ्या प्रस्थास प्रसूची म्हणतात. यावरून प्रसूची हा बहुपृष्ठकाचाच एक प्रकार आहे हे
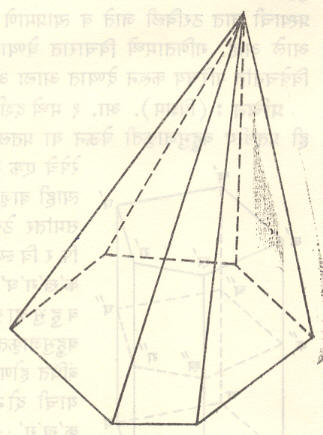 उघड आहे. या प्रस्थातील एक पृष्ठक बहुभुजाकृती असते हे वर आलेच आहे. या बहुभुजाकृतीला प्रसूचीचा पाया म्हणतात. प्रसूचीची इतर पृष्ठके त्रिकोण असतात व या सर्व त्रिकोणांना एक सामायिक शिरोबिंदू असतो. त्याला प्रसूचीचा शिरोबिंदू असे म्हणतात. पाया म्हणून बहुभुजाकृतीऐवजी वर्तुळ असेल, तर त्या प्रस्थाला सूची म्हणतात. शिरोबिंदूपासून पायावर टाकलेला लंब म्हणजे प्रसूचीची उंची होय. प्रसूचीचे घनफळ १/३ पाया × उंची या सूत्राने मिळते.
उघड आहे. या प्रस्थातील एक पृष्ठक बहुभुजाकृती असते हे वर आलेच आहे. या बहुभुजाकृतीला प्रसूचीचा पाया म्हणतात. प्रसूचीची इतर पृष्ठके त्रिकोण असतात व या सर्व त्रिकोणांना एक सामायिक शिरोबिंदू असतो. त्याला प्रसूचीचा शिरोबिंदू असे म्हणतात. पाया म्हणून बहुभुजाकृतीऐवजी वर्तुळ असेल, तर त्या प्रस्थाला सूची म्हणतात. शिरोबिंदूपासून पायावर टाकलेला लंब म्हणजे प्रसूचीची उंची होय. प्रसूचीचे घनफळ १/३ पाया × उंची या सूत्राने मिळते.
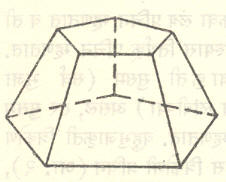 पायाला समांतर असलेल्या प्रतलाने प्रसूचीचा छेद घेतल्यास शिरोबिंदूकडील भाग प्रसूचीचा असेल परंतु पायाकडील भाग ‘समच्छिन्न’ होईल (आ. ५). याला भारतीय गणिती ब्रह्मगुप्त (इ. स. सातवे शतक) यांनी समखात असे नाव दिले आहे. समच्छिन्नाचे घनफळ १/३ उंची X (त + √ततʹ + तʹ) या सूत्राने मिळते. यामध्ये त आणि तʹयांनी तळांचे क्षेत्रफळ दर्शविले आहे. हे सूत्र ब्रह्मगुप्त यांच्या ग्रंथात दिलेले आहे. तळाला समांतर असलेल्या प्रतलांनी प्रसूचीचे छेद घेतल्यास ते तळाशी सरूप असतात व अशा छेदांची क्षेत्रफळेशिरोबिंदूपासून असणाऱ्या अंतराच्या वर्गाच्या प्रमाणात असतात. म्हणजेच तʹ/उʹ२ = त/उ२ (उʹ, उ – छेदांचे शिरोबिंदूपासूनचे अंतर).
पायाला समांतर असलेल्या प्रतलाने प्रसूचीचा छेद घेतल्यास शिरोबिंदूकडील भाग प्रसूचीचा असेल परंतु पायाकडील भाग ‘समच्छिन्न’ होईल (आ. ५). याला भारतीय गणिती ब्रह्मगुप्त (इ. स. सातवे शतक) यांनी समखात असे नाव दिले आहे. समच्छिन्नाचे घनफळ १/३ उंची X (त + √ततʹ + तʹ) या सूत्राने मिळते. यामध्ये त आणि तʹयांनी तळांचे क्षेत्रफळ दर्शविले आहे. हे सूत्र ब्रह्मगुप्त यांच्या ग्रंथात दिलेले आहे. तळाला समांतर असलेल्या प्रतलांनी प्रसूचीचे छेद घेतल्यास ते तळाशी सरूप असतात व अशा छेदांची क्षेत्रफळेशिरोबिंदूपासून असणाऱ्या अंतराच्या वर्गाच्या प्रमाणात असतात. म्हणजेच तʹ/उʹ२ = त/उ२ (उʹ, उ – छेदांचे शिरोबिंदूपासूनचे अंतर).
प्रसूचीचा पाया त्रिकोण असेल, तर अशा प्रसूचीला त्रिकोणी सूची म्हणतात. त्रिकोणी सूचीला चतुःपृष्ठक व चतुष्फलक ही नावेही रूढ आहेत. पाया चौरस असून बाजूच्या कडा समान असतील, तर त्या प्रसूचीला सुसम चौरस प्रसूची म्हणतात. ईजिप्तमधील पिरॅमिड सुसम चौरस प्रसूचीचे नमुने आहेत. प्रसूची तिर्यक्ही असू शकते.
बहुपृष्ठक : या प्रस्थास अनेक पृष्ठके असून ती पृष्ठके प्रतलीय बहुभुजाकृती असतात. त्याचे शिरोबिंदू ज्या प्रतलांमध्ये पडतात त्या प्रतलांची संख्या नेहमी सांत असते. बहुपृष्ठकाला असणाऱ्या पृष्ठकांच्या संख्येवरून त्यांना नावे देण्यात आलेली आहेत. चार पृष्ठके असल्यास चतुःपृष्ठक, पाच पृष्ठके असल्यास पंचपृष्ठक वगैरे. बहुपृष्ठकांतील कोणतेही दोन बिंदू सरळ रेषेने जोडले असता त्या रेषा खंडावरील सर्व बिंदू बहुपृष्ठकाचे घटकबिंदू असतील, तर अशा बहुपृष्ठकाला बहिर्वक्र बहुपृष्ठक म्हणतात. बहिर्वक्र बहुपृष्ठकाच्या बाबतीत लेनर्ड ऑयलर (१७०७–८३) यांचे पुढील सूत्र प्रसिद्ध आहे : श–क+प = २. येथे श ही शिरोबिंदूंची संख्या प – पृष्ठकांची संख्या व क –कडांची संख्या आहे. सुसम बहुपृष्ठके ही बहिर्वक्र बहुपृष्ठके असतात व त्यांची पृष्ठके एकरूप बहुभुजाकृती असतात. अशा बहुपृष्ठकांमध्ये प्रत्येक कडेवर होणारा द्वितल कोन [⟶ कोन] तोच असतो. एकमेकांशी एकरूप असलेल्या म बाजूंच्या ब सुसम बहुभुजाकृती घेऊन शिरोबिंदूंशी जोडून बहुपृष्ठक तयार केल्यास त्यामध्ये पुढील सूत्र सत्य असते : बश = २क = मप येथे श–शिरोबिंदूंची संख्या, क–कडांची संख्या, प–पृष्ठकांची संख्या आहे. वरील ऑयलर सूत्राचा उपयोग करून पुढील समकीरण मिळते.
|
१ |
+ |
१ |
= |
१ |
+ |
१ |
. |
|
ब |
म |
२ |
क |
यामध्ये ब आणि म यांची मूल्ये कमीत कमी तीन असावी लागतात कारण म तीनापेक्षा कमी असेल, तर बहुभुजाकृती तयार होणार नाही. तसेच ब तीनापेक्षा कमी असेल, तर प्रस्थ तयार होणार नाही. या समीकरणाचे निर्वाह (समीकरण सोडवून काढलेली उत्तरे) फक्त पाचच येतात. कारण कोणत्याही शिरोबिंदूपाशी होणाऱ्या प्रतल कोनांची बेरीज चार काटकोनांपेक्षा कमी असते. या प्रत्येक निर्वाहावरून मिळणाऱ्या सुसम बहुपृष्ठकाला ‘लोलक’ म्हणतात. लोलकाचे प्रकार पुढील कोष्टकात दिले आहेत. या सर्व लोलकांचा प्लेटो यांच्या Theaetetusया ग्रंथात उल्लेख आलेला असून (व त्यावरून त्यांना ‘प्लेटॉनिक प्रस्थ’ असे म्हणतात) यूक्लिड यांच्या Elementsया ग्रंथाच्या तेराव्या भागात त्यांचे विस्तृत वर्णन दिलेले आहे.
प्लेटॉनिक प्रस्थाचे (लोलकाचे) प्रकार व त्यांचे गुणधर्म
|
सुसम बहुपृष्ठकाचे नाव |
ब |
म |
श |
क |
प |
|
चतुःपृष्ठक |
३ |
३ |
४ |
६ |
४ |
|
घन (षट्फलक) |
३ |
४ |
८ |
१२ |
६ |
|
अष्टपृष्ठक |
४ |
३ |
६ |
१२ |
८ |
|
द्वादशपृष्ठक |
३ |
५ |
२० |
३० |
१२ |
|
विंशतिपृष्ठक |
५ |
३ |
१२ |
३० |
२० |
या पाचही सुसम बहुपृष्ठकांच्या शिरोबिंदूंचे जात्य सहनिर्देशक खाली दिल्याप्रमाणे घेता येतात :
चतुःपृष्ठक (१, १, १), (१, -१, -१), (-१, १, -१), (-१, -१, १).
घन (±१, ±१, ±१).
अष्टपृष्ठक (± १, ०, ०), (०, ±१, ०), (०, ०, ±१).
विंशतिपृष्ठक (±ट, ±१, ०), (०, ±ट, ±१), (±१, ०, ±ट).
द्वादशपृष्ठक (±ट२, ±१, ०), (०, ±ट२, ±१), (±१, ०, ±ट२), (±ट, ±ट, ±ट).
|
या ठिकाणी ट = |
√५ + १ |
|
२ |
वरील सुसम बहुपृष्ठकांच्या आकृत्या आ. ६ मध्ये दिल्या आहेत.
ज्याप्रमाणे बहुपृष्ठके ही द्विमितीय अवकाशातील बहुभुजाकृतींची त्रिमितीय अवकाशातील अनुरूपे आहेत त्याचप्रमाणे बहु-अधिपृष्ठके ही न-मितीय अवकाशातील

अनुरूपे आहेत. सामान्य बहु-अधिपृष्ठकाची (मितींची संख्या विचारात न घेता याला ढोबळपणे ‘बहु-पृष्ठक’ असेही कधीकधी म्हणतात) व्याख्या सामान्य प्रस्थाच्या व्याखेचे व्यापकीकरण करून ‘न–मितीय अवकाशाचा अधिप्रतलांनी बंधित केलेला सलग सांत भाग’ अशी देता येते. जर कोणतीही अतिरिक्त अधिप्रतले काढून टाकली, तर जी न–१ मितीय अधिप्रतले उरतात त्यांनी तयार झालेल्या बहु-अधिपृष्ठकाला कोश किंवा अधिपृष्ठके किंवा अधिफलक म्हणतात. उदा., बहुभुजाकृतीचे कोश म्हणजे त्याच्या बाजू असतात, तर बहुपृष्ठकाचे कोश म्हणजे त्याची पृष्ठके आणि चतुर्मितीय बहु-अधिपृष्ठकाचे कोश म्हणजे प्रस्थे होत. प्लेटॉनिक प्रस्थांसंबंधीच्या वरील विवरणाचेही न–मितीय अवकाशातील अनुरूप बहु-अधिपृष्ठकांकरिता व्यापकीकरण करता येते.
पहा : बहुभुजाकृति भूमिती स्फटिकविज्ञान.
संदर्भ : 1. Coxeter, H. S. M. Regular Polytopes, New York, 1963.
2. Liusternik, L. A. Trans. Smith, J. T. Convex Figures and Polyhedra, New York, 1963.
3. Toth, L. F. Regular Figures, New York, 1964.
गुर्जर, ल. वा.
“