अणु व आणवीय संरचना : रासायनिक मूलद्रव्यांचा मूलभूत घटक म्हणजे अणू होय. ग्रीक शब्द ‘ॲटम’ (अणू) याचा अर्थ ‘अविभाज्य’ असा आहे.
आधुनिक संशोधनाने अणूला रचना असते. तसेच त्याचे विभाजन होते असे सिद्ध झाले असले, तरी रासायनिक विक्रियांमध्ये भाग घेणारे अणू अविभाज्य राहतात.
पदार्थाचे स्वरूप अणुमय आहे ही कल्पना फार प्राचीन आहे. ग्रीकांमध्ये ल्युसिपस आणि डीमॉक्रिटस यांनी ख्रिस्तपूर्व ५ व्या शतकात सर्व पदार्थ अणू आणि अवकाश यांचे बनलेले आहेत, असे प्रतिपादन केले.
हिंदुस्थानात वैशेषिक तत्त्वज्ञानाचे प्रणेते कणाद यांच्या मताप्रमाणे सर्व इंद्रियसंवेद्य बाह्यद्रव्य नित्य, अविच्छेद्य व सूक्ष्म कणांनी म्हणजे अणूंनी बनलेले आहे. अणूंचा परस्परसंयोग होण्यास जेव्हा आरंभ होतो तेव्हा सृष्टीतील पदार्थ उत्पन्न होतात.
आधुनिक आणवीय उपपत्तीचे जनक डाल्टन (१७६६–१८४४) यांनीही सर्व पदार्थ नित्य, सूक्ष्म व अविभाज्य अशा अणूंचे बनलेले आहेत, अशी कल्पना मांडली. त्यांनी अणूंचे जे गुणधर्म गृहीत धरले, त्यामुळे प्रायोगिक निष्कर्षांचे विवरण करता आले व नवीन प्रयोगही सूचित झाले. डाल्टन यांच्या मतानुसार सर्व पदार्थ काही विवक्षित मूलद्रव्यांचे बनले आहेत. एका मूलद्रव्याचे सर्व अणू सर्वस्वी एकसारखेच असतात व त्यांचे द्रव्यमान सारखेच असते. भिन्नभिन्न मूलद्रव्यांचे अणू भिन्नभिन्न गुणधर्मांचे असतात. त्यांचे द्रव्यमान वेगळे असते. अणूंच्या संयोगाने रेणू तयार होतात व हे रेणू किंवा अणूही पदार्थाचे लहानांत लहान घटक असतात. प्रत्येक रेणूमध्ये निरनिराळ्या मूलद्रव्यांचे ठराविक संख्येचे अणू असतात. एकेका संयुगाचे रेणू सारखेच असतात परंतु निरनिराळ्या संयुगांचे रेणू निरनिराळे असतात. रासायनिक विक्रियांमध्ये मूळच्या रेणूचे अणूंत विभाजन होऊन अणूंच्या पुनर्रचनेने नवीन संयुगे तयार होतात. यामुळे कोणत्याही रासायनिक विक्रियेत सर्व मूळ अणूंची संख्या तीच रहाते व कोणतेही अणू नष्ट होत नाहीत.
या गृहीतांच्या आधारे डाल्टन यांना रासायनिक विक्रियांच्या संबंधातील दोन नियमांची संगती लावता आली. ते नियम म्हणजे (१) निश्चित प्रमाणांचा नियम व (२) गुणित प्रमाणांचा नियम [→ रासायनिक विक्रिया].
अणुभार व आणवीय द्रव्यमान : भौतिकी व रसायनशास्त्र या विषयांशी संबंधित असलेल्या आंतरराष्ट्रीय शास्त्रीय संस्थांनी कार्बन मूलद्रव्याच्या १२ अणुभार असलेल्या (C12) समस्थानिकाचा (अणुक्रमांक तोच पण अणुभार भिन्न असलेला त्या मूलद्रव्याच्या प्रकाराचा) अणुभार हा बरोबर १२ धरून त्यावरून काढलेल्या C12/१२ या एककावरून (चिन्ह u) इतर सर्व मूलद्रव्यांचे अणुभार निश्चित केले आहेत. या पद्धतीनुसार आणवीय द्रव्यमान एकक १·६६०×१०-२४ ग्रॅम व हायड्रोजन (H1)चे द्रव्यमान १·००७८२५ u इतके येते [→ अणुभार अणुक्रमांक आणवीय द्रव्यमान एकक].
अणुभार किंवा आणवीय द्रव्यमान निश्चित करण्याच्या रासायनिकपद्धती उपलब्ध असल्या तरी आता भौतिकीमध्ये द्रव्यमान वर्णपटलेखकाच्या [→ द्रव्यमान वर्णपटविज्ञान] साहाय्याने आणि अणुकेंद्रीय विक्रियांच्या अभ्यासामुळे आणवीय द्रव्यमाने अचूकतेने निश्चित करतात आणि त्यांच्या सारण्या उपलब्ध आहेत.
अणुक्रमांक : मेंडेलेव्ह यांनी तयार केलेल्या ⇨ आवर्त सारणीतील मूलद्रव्याच्या क्रमांकाला त्या मूलद्रव्याचा ⇨ अणुक्रमांक म्हणतात. पुढे या क्रमांकांत काही फेरफार करावे लागले. आधुनिक संशोधनाने आणवीय संरचना आता निश्चित झाली आहे. त्याप्रमाणे अणुक्रमांक म्हणजे केंद्रस्थानी असणाऱ्या प्रोटॉनांची संख्या होय. अणुक्रमांक Z या अक्षराने दर्शवितात. अणूचे रासायनिक स्वरूप या प्रोटॉन-संख्येवरून ठरते. विद्युत् रहित अणूमध्ये केंद्रबाह्य इलेक्ट्रॉनांची संख्याही अणुक्रमांकाइतकीच असते.
अणूचे घटक : केंद्रीय अणू : इलेक्ट्रॉन (ऋण किरण), धन किरण, क्ष-किरण आणि किरणोत्सर्ग (अणुकेंद्र फुटून त्यातून कण वा किरण बाहेर पडणे) यासंबंधी झालेल्या संशोधनावरून असे दिसून आले की, मूलद्रव्यांचे अणू हे काही घटक-कणांचे झालेले असले पाहिजेत [ → ऋण किरण धन किरण किरणोत्सर्ग]. ऋण किरणांच्या अभ्यासाने इलेक्ट्रॉन हे सर्व अणूंचे सामान्य घटक असले पाहिजेत, असे दिसून आले. या इलेक्ट्रॉनांचे द्रव्यमान (mo) हायड्रोजन-अणुभाराच्या सु. १,८३७ पटींनी लहान आढळले म्हणजे विद्युत् भाररहित अणूंचे बहुतेक सर्व द्रव्यमान त्यांच्या धन भाराशी निगडीत असले पाहिजे, असे अनुमान निघते.
अणूंच्या घटकांच्या अभ्यासास व त्यांच्या द्रव्यमान मापनास जे. जे. टॉमसन (१८५६–१९४०) यांनी सुरुवात केलेल्या धन किरणांच्या संशोधनाने गती मिळाली व त्याचे पर्यवसान ॲस्टन यांच्या द्रव्यमान वर्णपटलेखकात झाले. याचेच प्रगत स्वरूप म्हणजे डेम्स्टर किंवा नीर यांचे द्रव्यमान वर्णपटलेखक होत. त्यांच्या उपयोगाने अचूक अशी आणवीय द्रव्यमाने प्राप्त झाली आहेत आणि समस्थानिकांचीही माहिती मिळाली आहे. [→द्रव्यमान वर्णपटविज्ञान].
क्ष-किरण-प्रकीर्णनाने (विखुरण्यामुळे) अणूच्या धन भाराची माहिती मिळाली आणि त्यांच्या वर्णपटांवरून अणुक्रमांक निश्चित झाले. अणुक्रमांक व धन भार यांचा संबंधही स्पष्ट झाला. किरणोत्सर्गी द्रव्यातून इलेक्ट्रॉन व धन आल्फा कण बाहेर पडतात. आल्फा कण अतिशय आयनकारक (विद्युत् भारित अणू वा रेणू वेगळे सुटे करणारे) असतात. त्यांचा विद्युत् भार इलेक्ट्रॉनाच्या दुप्पट व द्रव्यमान हायड्रोजनाच्या चौपट म्हणजे हीलियम-अणूइतके असते. आल्फा कण आपल्या पल्ल्याच्या अखेरीस आपल्या सरळ मार्गापासून काही वेळा एकदम विचलित होतात, असे आढळून आले. हे विचलन अणुकेंद्राच्या विद्युत् भारामुळे होणाऱ्या आल्फा-कणांच्या कुलंब-प्रतिसारणाने घडत असते.
१९०४ मध्ये नगाओका या जपानी शास्त्रज्ञांनी अणूमधील इलेक्ट्रॉन सूर्याभोवती फिरणाऱ्या ग्रहांप्रमाणे धन विद्युत् भारित केंद्राभोवती फिरत असावेत, अशी कल्पना मांडली. परंतु मॅक्सवेल यांच्या विद्युत् कर्षुकीय सिद्धांताप्रमाणे ही रचना आणवीय स्थैर्याला विघातक होते म्हणून मान्य झाली नाही. तेव्हा अणूमधील धन भार असतो तरी कोठे, याचे संशोधन आल्फा-प्रकीर्णन-प्रयोगांनी करण्याचे रदरफर्ड (१९११) यांनी ठरविले.
अणूचा सर्व विद्युत् भार एका केंद्रस्थानी एकत्रित झाला असावा आणि त्याच्याभोवती इलेक्ट्रॉन फिरत असावेत, असे गृहीत धरून आल्फा कणांचे प्रकीर्णन कसे होईल याचे गणित रदरफर्ड यांनी केले. आपात दिशेशी (लक्ष्यावर आल्फा कण ज्या दिशेने पडतात त्या दिशेशी) θ व θ +dθ हे कोन करणाऱ्या रेषांच्या दरम्यान प्रकीर्ण होणाऱ्या आल्फा कणांची संख्या पुढील समीकरणाने मिळते :
|
Nθ= |
N0 π nt(Ze)2·(2e)2 |
· |
cot |
( |
θ |
) |
cosec2 |
( |
θ |
) |
dθ |
||
|
4E2 (4π μ0)2 |
2 |
2 |
|||||||||||
… (१)
येथे Nθ= θ व θ+dθ यांच्या दरम्यान प्रकीर्ण होणाऱ्या आल्फाकणांची संख्या N०= आपाती आल्फा कण संख्या, n=लक्ष्य पदार्थातील प्रति घ. सेंमी. मधील अणू, t= लक्ष्याची जाडी, Ze= अणूचा धन विद्युत् भार, e = इलेक्ट्रॉनाचा विद्युत् भार, 2e = आल्फा कणाचा विद्युत् भार, E= आल्फा कणांची गतिज ऊर्जा, εo= निर्वाताची विद्युत् पार्यता (आरपार जाण्याची क्षमता).
रदरफर्ड यांचे साहाय्यक गायगर आणि मार्सडेन यांनी केलेल्या प्रयोगांत वरील सूत्राचा पडताळा आला. विशेषत: पाठीमागे किंवा विशाल कोन करून प्रकीर्ण होणाऱ्या आल्फा कणांची संख्या या सूत्राशी जुळणारी आढळली. या प्रयोगावरून अणुकेंद्राची त्रिज्या सुमारे १०-१२ सेंमी. या मानाची म्हणजे अणुत्रिज्येच्या १०-४ पट इतकी सूक्ष्म आढळली. त्याचप्रमाणे केंद्रीय विद्युत् भार हाही निश्चित होऊन तो इलेक्ट्रॉनाच्या Z पटीने म्हणजे अणुक्रमांकाच्या पटीने असतो हे सिद्ध झाले. या प्रकारे सिद्ध झालेल्या अणूच्या प्रतिमानास ‘रदरफर्ड अणू’ असेही म्हणतात.
द्रव्यमानांक आणवीय संरचना : अणूंची द्रव्यमाने आणवीय द्रव्यमान एककांमध्ये पूर्णांकांत मांडता येत नाहीत. आणवीय द्रव्यमानाच्या निकटचा जो पूर्णांक तो ⇨द्रव्यमानांक (A) होय. याप्रमाणे हायड्रोजनाचा अणुक्रमांक १ व द्रव्यमानांक १ येईल. ऑक्सिजनाचा अणुक्रमांक ८ व द्रव्यमानांक १६ युरेनियमाचा अणुक्रमांक ९२ व द्रव्यमानांक २३८ असे आहेत. हायड्रोजनाच्या अणुकेंद्रास ‘प्रोटॉन’ हे नाव दिले आहे. अणुकेंद्रीय द्रव्यमान A आणि विद्युत् भार Ze यांची संगती लावण्याकरिता केंद्रास्थानी A प्रोटॉन मानले, तर विद्युत् भार Ze इतकाच मिळविण्यासाठी त्यामध्ये A–Z इतके इलेक्ट्रॉन मानावे लागतील. त्यामुळे केंद्राचे द्रव्यमान न वाढता विद्युत् भार हवा तो प्राप्त होईल. याप्रमाणे केंद्रस्थानी एकून 2 A–Z इतके कण व केंद्रबाह्य Z इलेक्ट्रॉन अशी संरचना होईल. परंतु तरंगयामिकी [→ पुंजयामिकी] प्रस्थापित झाल्यावर अणुकेंद्र-त्रिज्या, ⇨अनिश्चिततेचे तत्त्व, अणुकेंद्रीय परिवलन परिबल व इलेक्ट्रॉनाचे परिवलन परिबल [→अणुकेंद्रीय व आणवीय परिबले], इलेक्ट्रॉनांचे व केंद्राचे सांख्यिकीय वर्तन, त्याचे कर्षुकीय परिबल या सर्वांचा विचार करता, केंद्रस्थानी इलेक्ट्रॉन असणे सुसंगत ठरत नाही. द्रव्यमानांक हा अणुकेंद्रातील कणांची एकूण संख्या दर्शवितो. केंद्रस्थानी प्रोटॉनांबरोबरच सु. त्याच द्रव्यमानाचे पण विद्युत् भाररहित न्यूट्रॉन हे मूलकणही असावेत, ही कल्पना रदरफर्ड यांनी १९२० मध्येच मांडली होती. पण त्यास त्या वेळी सैद्धांतिक किंवा प्रायोगिक आधार नव्हता. न्यूट्रॉनाचा शोध १९३२ मध्ये लागल्यानंतर आणवीय संरचनेचे कोडे सुटले. न्यूट्रॉनाच्या केंद्रीय अस्तित्वामुळे समस्थानिकांचाही उलगडा होतो. मूलद्रव्याचे रासायनिक गुणधर्म त्याच्या अणुक्रमांकावर म्हणजे Z या केंद्रीय प्रोटॉनांच्या संख्येवर अवलंबून असतात. त्यामुळे केंद्रीय न्यूट्रॉनसंख्या बदलली तर द्रव्यमान बदलते पण मूलद्रव्य तेच राहते. याप्रमाणे केंद्रस्थानी द्रव्यमानांक A इतके कण असून त्यांपैकी Z प्रोटॉन असतात व A–Z न्यूट्रॉन असतात आणि केंद्राच्या बाहेर Z इलेक्ट्रॉन फिरतात, अशी आणवीय संरचना आता निश्चित झाली आहे.
अणुकेंद्राचे स्थैर्य :द्रव्यमान-क्षय : रासायनिक विक्रियांमध्ये अणू स्थिरच असतात. त्यांची संयुगे तयार होतात. मात्र केंद्रबाह्य इलेक्ट्रॉनांच्या पुनर्रचनेमुळे संयुगांच्या रेणूतील निरनिराळ्या अणूंमध्ये बंध उत्पन्न होऊन संयुगांना स्थैर्य प्राप्त होते. कोणत्याही स्थिर अणुकेंद्राचे द्रव्यमान त्यातील सुट्या प्रोटॉन व न्यूट्रॉन कणांच्या एकूण द्रव्यमानापेक्षा कमी भरते. आइन्स्टाइन यांच्या E=mc2 (E=ऊर्जा, m=द्रव्यमान, c=प्रकाशाचा वेग) या सूत्राप्रमाणे द्रव्यामानाचे ऊर्जेत रूपांतर होत असते. वर उल्लेखलेला द्रव्यमानातील फरक ऊर्जेत रूपांतरित होऊन ती केंद्रीय प्रोटॉन–न्यूट्रॉनांमध्ये बंध उत्पन्न करण्यासाठी उपयोगी पडते.
बोर-अणू : अणूच्या स्थिर स्थिती :मूलद्रव्यांचे परस्परसंबंध त्यांच्यारासायनिक गुणधर्मांवरून स्पष्ट होतात आणि मूलद्रव्यांच्या उत्सर्जन व शोषण-वर्णपटातील वर्णरेषा तद्विशिष्ट असतात [→ वर्णपटविज्ञान]. वर्णरेषांची उपपत्ती अणूतील इलेक्ट्रॉनांच्या रचनेवरून ठरविता आली तर त्याच रचनेप्रमाणे रासायनिक गुणधर्मांचेही स्पष्टीकरण करता येईल. अणुकेंद्राभोवती इलेक्ट्रॉन फिरत असतील तर ते प्रवेगित असले पाहिजेत आणि मॅक्सवेल-सिद्धांताप्रमाणे प्रवेगित इलेक्ट्रॉन प्रारण (विद्युत् कर्षुकीय तरंगरूपातील ऊर्जा) उत्सर्जित करील व अणूचे स्थैर्य बिघडेल.
माक्स प्लांक यांच्या ऊष्मीय प्रारणाच्या (इ.स. १९००) आणि आइनस्टाइन यांच्या प्रकाशविद्युत् परिणामाच्या उपपत्तीप्रमाणे (१९०५) प्रारणाचे उत्सर्जन वा शोषण पुंजरूपाने होत असते व पुंजाची ऊर्जा E = hν या सूत्राने मिळते येथे ν ही प्रारणाची कंप्रता (प्रारणातील प्रतिसेकंदास होणाऱ्या तरंगसंख्या) व h हा प्लांक स्थिरांक आहे. कोणताही प्रारणशील संच एका ऊर्जास्थितीतून दुसऱ्या स्थितीमध्ये गेला तर प्रारणाचे उत्सर्जन किंवा शोषण होईल. अणूचे स्थैर्य व तद्विशिष्ट प्रारण यांचा मेळ कसा घालावा, हा मुख्य प्रश्न होता व तो बोर यांनी वरील कल्पनांच्या आधारे सोडविला. हायड्रोजन या सर्वांत हलक्या अणूचा क्रमांक १ असून त्याच्या केंद्रस्थानी १ प्रोटॉन व केंद्राबाहेर १ इलेक्ट्रॉन असतो. हायड्रोजन-वर्णपटाच्या उपपत्तीकरिता बोर यांनी दोन गृहीते मांडली (१९१३). ती अशी : (१) अणुकेंद्राभोवती फिरणारे इलेक्ट्रॉन जर ठराविक भ्रमण-कक्षेत फिरत असले, तर ते प्रवेगित असले तरीही प्रारणाचे उत्सर्जन होत नाही. त्यांच्या अशा स्थितीस ‘स्थिर स्थिती’ म्हणतात. स्थिर स्थितीतील इलेक्ट्रॉनाच्या बाबतीत पुढील पुंजीय अटींची पूर्तता झाली पाहिजे. कोनीय संवेग
(निरूढी परिबल Χ कोनीय वेग = nh/2π आणि n=कोणताही पूर्णांक. (२) इलेक्ट्रॉनांचे एक स्थिर स्थितीतून दुसऱ्या स्थिर स्थितीत संक्रमण झाले, तरच प्रारणाचे उत्सर्जन किंवा शोषण होईल व प्रारणाची कंप्रता hν = E1-E2या सूत्राने मिळेल (E= इलेक्ट्रॉनाची एका स्थिर स्थितीतील ऊर्जा), बोर यांच्या कल्पनेप्रमाणे स्थिर कक्षा वर्तुळाकार मानल्यास तिची त्रिज्या पुंजीय अटींच्या पूर्ततेने मिळेल ती अशी :
|
कोनीय संवेग |
Iw |
= |
m0vr |
= |
n |
( |
h |
) |
|
2π |
|
किंवा |
m0vr |
= |
nh/2π ….(2) |
येथे r = भ्रमण-कक्षेची त्रिज्या, mo=इलेक्ट्रॉनाचे द्रव्यमान, ν =इलेक्ट्रॉनाचा वेग, n =भ्रमण-कक्षेचा पुंजांक (पृथक् मूल्ये घेणाऱ्या म्हणजेच पुंजरूप असलेल्या राशींच्या निरनिराळ्या मूल्यांपैकी एक मूल्यदर्शक अंक म्हणजे पुजांक होय). भ्रमण-कक्षेतील अभिमध्य प्रेरणा
(वर्तुळाच्या मध्याकडे जाणारी प्रेरणा) कुलंब-आकर्षणामुळे उत्पन्न होते
|
(Ze)2 |
= |
m0ν2 |
…(३) |
|
(4 π μ0)2 |
म्हणून येथे Z हा अणुक्रमांक, e हा इलेक्ट्रॉनावरील विद्युत् भार व μ0 = निर्वाताचीविद्युत् पार्यता आहे. स्थिर कक्षेची त्रिज्या आणि इलेक्ट्रॉनाचा वेग (२) आणि (३) वरून मिळतात.
|
r |
= |
n2h2(4 π μ0) |
ν |
= |
rw |
= |
2 π Ze2 |
…(४) |
|
|
4 π2m0Ze2 |
(4 π μ0)nh |
इलेक्ट्रॉनाची एकूण ऊर्जा = स्थितिज ऊर्जा + गतिज ऊर्जा
|
E |
= |
-Ze2 |
+ |
1/2m0 ν2 |
= |
-2 π2m0Z2e4 |
…(५) |
|
(4 πμ0)r |
(4πμ0)2n2h2 |
पुंजांक n2च्या स्थिर स्थितीतून n1च्या दुसऱ्या स्थिर स्थितीत इलेक्ट्रॉनाचे संक्रमण झाल्यास बोर यांच्या दुसऱ्या गृहीताप्रमाणे प्रारण होईल.
|
hν |
= |
E2-E1 |
= |
2 π2m0Z2e4 |
( |
1 |
– |
1 |
) |
…(६) |
|
(4πμ0)2h2 |
n12 |
n22 |
वर्णपटविज्ञानातील प्रथेप्रमाणे तरंगांक (तरंगलांबीचा व्यस्तांक) ⊽= ν/c (c = प्रकाशवेग) याकरिता पुढील सूत्र मिळते :
|
⊽ |
= |
hν |
= |
2π2m0Z2e4 |
( |
1 |
– |
1 |
) |
…(७) |
|
hc |
h3c(4π μ0)2 |
n12 |
n22 |
|
⊽ |
= |
E2 |
– |
E1 |
= |
T1-T2 |
T |
= |
– |
E |
|
|
hc |
hc |
hc |
किंवा
या राशीस ‘वर्णपट पद’ अशी संज्ञा आहे. वरील तरंगांकाचे सूत्र हे एका व्यापक तत्त्वाचे उदाहरण आहे.रिट्स यांच्या संयोग तत्त्वाप्रमाणे (१९०८) कोणत्याही वर्णरेषेचा तरंगांक दोन वर्णपट पदांच्या फरकाने दर्शविता येतो. हायड्रोजन-वर्णरेषेसाठी
|
T |
= |
– |
E |
= |
– |
2π2m0Z2e4 |
∙ |
1 |
= |
– |
R |
} |
…(८) |
|
hc |
h3c(4πμ0)2 |
n2 |
n2 |
||||||||||
|
R |
= |
2π2m0Z2e4 |
|||||||||||
|
h3c(4πμ0)2 |
|||||||||||||
R या राशीस ‘रिडबर्ग स्थिरांक’ म्हणतात.
बोर सदृशतेचे तत्त्व : इलेक्ट्रॉनाच्या कक्षेमध्ये होणाऱ्या भ्रमणांची आवृत्तिसंख्या आणि कक्षा बदलल्यामुळे होणाऱ्या प्रारणाची (अथवा शोषणाची) कंप्रता यांचा काहीही संबंध नाही. तरीसुद्धा स्थिर ऊर्जाअवस्थेला इलेक्ट्रॉनाच्या स्थिर कक्षेचे दृश्य रूप देण्याच्या प्रयत्नामुळे पुंजयामिकी व रूढ-यामिकी यांमधील साधर्म्य स्पष्ट होऊ लागले. मोठ्या पुंजांकांच्या (n →∞) स्थिरावस्थेचा विचार करता, एका स्थिर कक्षेमधून दुसऱ्या निकटच्या कक्षेमध्ये इलेक्ट्रॉनाचे संक्रमण होताना निर्माण होणाऱ्या प्रारणाची कंप्रता आणि त्या कक्षेमध्ये होणाऱ्या इलेक्ट्रॉनाच्या भ्रमणांची आवृत्तिसंख्या ही एकच येतात, असे वरील R च्या मूल्यावरून व (४) या समीकरणावरून दिसून येते. पुंजयामिकीची गृहीते निश्चित करण्यासाठी बोर यांनी मांडलेल्या या सदृशतेच्या तत्त्वाचा व्यापक प्रमाणावर उपयोग झाला आहे.
केंद्रीय द्रव्यमानाचा विचार : केंद्रीय द्रव्यमान सांत (मर्यादित) असल्यामुळे प्रत्यक्षात अणुकेंद्र व इलेक्ट्रॉन त्यांच्या द्रव्यमान मध्याभोवती फिरत असतात. हे लक्षात घेता वरील समीकरणामध्ये moच्या ऐवजी न्यूनीकृत द्रव्यमान m0/(1 + m0/M) हे वापरल्यास कंप्रता अचूक येतात. येथे M हे अनुकेंद्राचे द्रव्यमान आहे. वरील समीकरणे हायड्रोजनाचे तीन समस्थानिक H1, H2, H3 यांच्या वर्णपटांकरिता व He4 म्हणजे हीलियम आयनाकरिता वापरल्यास हायड्रोजन-वर्णपटातील समस्थानिकामुळे उत्पन्न होणाऱ्या वर्णरेषा-रचनेचा आणि हीलियम-आयन-वर्णरेषांचा उलगडा होतो. जड हायड्रोजनाचा (डयूटेरियमाचा) शोध प्रथम या वर्णरेषांच्या रचनेमुळे लागला. हायड्रोजनाकरिता Z=1 आणि हीलियमाकरिता Z=2 ही मूल्ये वापरावी लागतात आणि त्याप्रमाणे रिडबर्ग स्थिरांक R ची RH आणि RHeअशी दोन मूल्ये मिळतात. वर्णरेषांची रचना, त्यांची जाडी वगैरे गोष्टींची संगती निव्वळ बोर-अणूच्या प्रतिमानाप्रमाणे मिळत नाही. प्रत्येक स्थिरावस्थेला अनुरूप इलेक्ट्रॉन स्थिर कक्षेकरिता एक ऊर्जा-पातळी असते. तत्सदृश ऊर्जा समीकरण (८) प्रमाणे –Rhc/n2 असते. n=1 ही कक्षा सर्वांत लहान व तिची त्रिज्या समीकरण (४) प्रमाणे हायड्रोजन-अणूमध्ये सु. ०·५ A0 (अँगस्टॉम एकक
A0=10-८ सेंमी.) म्हणजे ०·५ × १०-८ सेंमी. येते. ऊर्जा-पातळ्या इतक्या साध्या आहेत असे मानल्यास वर्णरेषांच्या सूक्ष्म रचनेची उपपत्ती देता येणार नाही.
अणूचे आकारमान : द्रव्याच्या गत्यात्मक सिद्धांतानुसार रेणूची त्रिज्या १ ते २ A0इतकी आढळते. अणूचा व्यासही पहिल्या बोर-त्रिज्येवरून १ A0 मानाचा येतो. जितकी त्रिज्या मोठी तितका विस्तार मोठा.
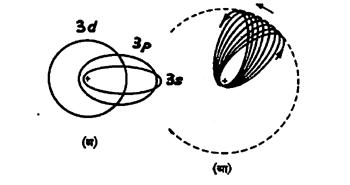
झोमरफेल्ड-उपपत्ती : पुंजीय अटींची पूर्तता करूनही प्रत्येक पुंजांकाच्या वर्तुळाकार कक्षेला अनुरूप इतर विवृत्त (लंबवर्तुळाकार) कक्षांचा गट संभवनीय आहे, असे झोमरफेल्ड यांनी सिद्ध केले. या सर्वांचे दीर्घ अक्ष सारखेच पण विकेंद्रता [→विवृत्त] निरनिराळी असते. लघु-अक्ष/दीर्घ-अक्ष हे गुणोत्तर (ι+1)/n या अपूर्णांकाने मिळते ι हा विवक्षित विवृत्त-कक्षेचा वलन-पुंजांक (परिभ्रमण पुंजांक) होय. या वलन-पुजांकांची मूल्ये शून्यापासून प्रमुख पुंजांक n उणे १ पर्यंत, पूर्णांकांत असली पाहिजेत. ⇨सापेक्षता सिद्धांताप्रमाणे प्रकाशवेगाच्या जवळपास वेग असल्यास इलेक्ट्रॉनाचे द्रव्यमान वाढते आणि म्हणून अतिविकेंद्रता असल्यास इलेक्ट्रॉन ज्या वेळी केंद्राच्या समीपतम असेल त्या वेळी त्याचे द्रव्यमान वाढते आणि एकूण ऊर्जा थोडी कमी होते, यामुळे वर्णरेषेच्या रुंदावण्याचा थोडासा उलगडा झाला परंतु सूक्ष्म रचनेचा उलगडा होईना. अतिविकेंद्रता असलेल्या कक्षांचे परांचन (परिभ्रमण अक्षाच्या गतीने शंक्वाकार निर्माण होणे) होत असते (पहा : आ. १).
ऊर्जा-पातळ्यांमधील संभवनीय संक्रमणाकरिता (ι मधील बदल) Δ ι =± 1 हा निवडीचा नियम संभाळला पाहिजे. ι = ०, १, २, ३,…यांना अनुक्रमे s, p, d, ƒ,… कक्षा अशी नावे दिली आहेत.
अणूचे सदिश-प्रतिमान : कक्षाविशिष्ट पुंजांक : झोमरफेल्ड यांच्या कल्पनेचा हायड्रोजनाच्या वर्णपटाचे स्पष्टीकरण करण्याकरिता विशेष उपयोग झाला, तरी इलेक्ट्रॉन-कक्षा केवळ वर्तुळाकार असल्या पाहिजेत असे नाही, तर एकाच प्रमुख पुंजांकाला अनुरूप अनेक कक्षा असू शकतील, ही कल्पना फार महत्त्वाची आहे. पुंजयामिकीप्रमाणे ऊर्जा-पातळ्यांना रचना असण्याची शक्यता सिद्ध झाली आणि एका विवक्षित ऊर्जा-पातळीकरिता प्रमुख पुंजांकाव्यतिरिक्त इतर पुंजांकांची आवश्यकता निर्माण झाली.
पुंजयामिकीच्या साहाय्याने कणाच्या अथवा कणसमूहाच्या विश्लेषणातून काही पुंजांक आपोआपच उपस्थित होतात. सदिश-प्रतिमानाच्या गृहीतान्वये या पुंजांकांचे आकलन उत्तम रीतीने होते. या गृहीतान्वये या पुंजयामिकीतील गणिताला मूर्त स्वरूप मिळाल्यासारखे होते.
हायड्रोजनाची प्रत्येक वर्णरेषा द्विक (दोघांची जोडी) असल्याचे सूक्ष्म परीक्षणांती आढळून आले आहे. सोडियमासारख्या क्षार (अल्कली) मूलद्रव्याचे रेषावर्णपट रेषायुग्माचे असतात. म्हणून तत्संबंधी ऊर्जा-पातळ्यांचीही द्विके असली पाहिजेत. याला रेषांची ‘सूक्ष्म रचना’ म्हणतात. याच्या विवरणाकरिता ऊलेनबेक आणि गूट्श्मिट यांनी इलेक्ट्रॉनाला कक्षेतील परिभ्रमणाव्यतिरिक्त अंगभूत असे परिवलन-परिबल
|
1 |
ħ |
( |
= |
1 |
h |
) |
|
2 |
2 |
2 π |
व म्हणून त्यामुळे निर्माण झालेले कर्षुकीय परिबल असले eħ
2m0 पाहिजे, असे गृहीत धरले. डिरॅक यांच्या सापेक्षीय पुंजयामिकीप्रमाणे इलेक्ट्रॉनाकरिता परिवलन परिबल आपोआपच प्राप्त होते, यासाठी परिवलन परिबलांक s = 1/2 धरावा लागतो. प्रकाशाचा उगम कर्षुकीय क्षेत्रात ठेवला, तर वर्णरेषा विभागून नवीन वर्णरेषा उत्पन्न होतात व त्यांना सूक्ष्म रचना प्राप्त होते [→ अणुकेंद्रीय व आणवीय परिबले]. या विभाजनाच्या विवरणाकरिता कर्षुकीय परिवलन परिबलांक ms हा पुंजांक मानावा लागतो. याखेरीज ι या परिभ्रमण सदिशाचे कर्षुकीय क्षेत्राच्या दिशेवरील प्रक्षेपाचे संख्यात्मक मूल्य mι हा कर्षुकीय परिभ्रमण पुंजांक महत्त्वाचा आहे. विविक्षित n आणि ι करिता mlι ची मूल्ये ι, ι-1,.., ..0,.., -(ι-1),-ι अशी एकूण 2 ι +1 येतात. प्रत्येक मूल्यास अनुरूप असे, कर्षुकीय दिशा आणि कक्षा-प्रतलाच्या (पातळीच्या) प्रलंबाची (लंबरेषेची) दिशा यांमधील कोनाचे मूल्य असते. याप्रमाणे इलेक्ट्रॉन-कक्षाविशिष्ट असे n, ι, mι व ms व हे चार पुंजांक असतात. इलेक्ट्रॉनाची अणूमधील ऊर्जा-पातळी या चार पुंजांकांनी निश्चित होते.
अणूमधील इलेक्ट्रॉन म्हणजे परिवलन-कर्षुकीय परिबल असलेला लहानसा कर्षुक मानावयास हरकत नाही. परिभ्रमण-कक्षा-प्रतलाची दिशा इलेक्ट्रॉनाच्या परिवलन आणि कक्षीय परिभ्रमण यांच्या एकत्रित परिबलाच्या दिशेवर अवलंबून राहते. बाह्य कर्षुकीय क्षेत्रात ही दिशा वर दिल्याप्रमाणे mι या पुंजांकावर अवलंबून असते. बाह्य क्षेत्र नसले, तरीही संभाव्य भ्रमण-कक्षांच्या प्रतलांच्या दिशांचा याच प्रकारे अंदाज करता येतो. ऊर्जा-पातळ्यांचे पुंजाक निराळे असूनसुद्धा एकत्रित ऊर्जा तीच असणे शक्य आहे. अशा ऊर्जा-समूहाला ‘अपभ्रष्ट-समूह’ म्हणतात.
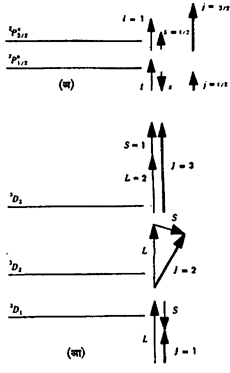
परिवलन-कक्षीय परिभ्रमण-संयोग : इलेक्ट्रॉनाच्या परिवलनाचा त्याच्या कक्षीय परिभ्रमणाशी संयोग होतो. त्याला परिवलन-कक्षीय परिभ्रमण-संयोग म्हणतात. पुंजयामिकीप्रमाणे एकूण पुंजांक j म्हणजे ι± s यांच्या दिशा अशा असतात की, त्यांतील फरक पूर्णांक असतो. म्हणून s हा ι यास समांतर किंवा प्रतिसमांतर (समांतर पण दिशा विरुद्ध असलेला) असतो. p इलेक्ट्रॉनाकरिता, म्हणजे ι = 1 आणि s = 1/2 असता, j च्या दिशा कोणत्या असू शकतात, ते सदिश-प्रतिमानाने आ.२ मध्ये दाखवले आहे. तत्सद्दश वर्णपटीय पदे व पातळ्या त्या त्या सदिशाजवळ दाखविल्या आहेत. त्यांची नावे नेहमीच्या वर्णपटविज्ञानाच्या प्रथेप्रमाणे आहेत. मोठी अक्षरे कणसमूहाच्या एकत्रित पुंजांकांकरिता व लहान अक्षरे सुट्या कणांकरिता वापरतात.
निरनिराळ्या कक्षांतील इलेक्ट्रॉन आणि त्यांची परिवलने याचा विचार करता रसेल-साँडर्स किंवा LS-संयोगाची शक्यता दिसते म्हणजे प्रथम सर्व इलेक्ट्रॉनांचे ι, सदिश पद्धतीने एकत्रित करून L काढणे, त्याचप्रमाणे s एकत्र करून S काढणे आणि L व S यांचा संयोग करणे. हलक्या अणूंच्या नीच ऊर्जा-पातळ्यांकरिता ही पद्धत लागू पडते.
दुसरी पद्धत म्हणजे j–j संयोग. प्रथम प्रत्येक इलेक्ट्रॉनाचा
j = ι± s काढून नंतर सर्व j सदिशरीत्या एकत्रित करण्याची ही पद्धत आहे. ही क्वचितच आढळते. पण मोठ्या द्रव्यमानांच्या अणूंमध्ये LS आणि j–j या दोहोंमधील पद्धत लागू पडते.
स्टर्न-गेर्लाख प्रयोग : इलेक्ट्रॉनाच्या कक्षीय परिभ्रमणगतीमुळे आणि इलेक्ट्रॉनाच्या अंगभूत परिवलनामुळे अणूला परिवलन-परिबल प्राप्त होते. याचा प्रत्यक्ष पुरावा स्टर्न-गेर्लाख प्रयोगाने मिळतो [→ अणुकेंद्रीय व आणवीय परिबले]. निरनिराळ्या ऊर्जा-पातळ्यांचा पुरावा फ्रँक आणि हर्ट्झ यांनी केलेल्या प्रयोगाने मिळतो.
पाउली विवर्जन-तत्त्व : आणवीय संरचना : पाउली यांच्या विवर्जन (वर्ज्य करणाऱ्या) तत्त्वाप्रमाणे एकाच ऊर्जा-पातळीमध्ये दोन इलेक्ट्रॉन असू शकणार नाहीत म्हणजे एकाच अणूमध्ये ज्यांचे चारही पुंजांक n, ι, mι, ms किंवा n, ι, j, mj सारखेच आहेत, असे दोन इलेक्ट्रॉन असणे शक्य नाही. प्रत्येक प्रमुख n करिता ι ची 0 ते (n-1) अशी मूल्ये असतात. प्रत्येक ι करिता mι
ची –ι, –ι+1,..,0,…, ι-1, ι अशी 2ι +1 इतकी मूल्ये असतात व या प्रत्येकासाठी ms ची (±1/2 ) दोन मूल्ये असतात. म्हणून n पुजांक असणाऱ्या संभाव्य ऊर्जा-पातळ्या एकूण 2n2 असतात व त्यांच्यामध्ये 2n2 इलेक्ट्रॉन असतील. असे सर्व इलेक्ट्रॉन मिळून n पुंजांक असलेले कवच तयार होते. अशा तऱ्हेने निरनिराळे अणू निर्माण होतात. कवचामध्ये 2n2 इलेक्ट्रॉन असतील तर ते कवच पूर्ण होईल. एखादे अंतर्गत कवच पूर्ण होण्यापूर्वीच केव्हा केव्हा बाहेरचे कवच आधी भरू लागते. याचे एक कारण म्हणजे अतिविकेंद्रता असलेल्या काही इलेक्ट्रॉन-कक्षांच्या अंतर्भेदामुळे इलेक्ट्रॉन अणुकेंद्राच्या अगदी जवळ जातात. त्यांचे द्रव्यमान वाढते व पातळीची ऊर्जा कमी होते. ही आणवीय इलेक्ट्रॉनाची कवच-रचना आवर्त-सारणीमध्ये दिलेल्या माहितीवरून स्पष्ट होईल (कोष्टक पहावे). उदा., मूलद्रव्य 24Cr मध्ये पाच 3d इलेक्ट्रॉन व बाकीचे 19K प्रमाणे 25Mn मध्ये पाच 3d इलेक्ट्रॉन व बाकीचे 20Ca प्रमाणे 47Ag मध्ये एक 5s इलेक्ट्रॉन व बाकीचे 46pd प्रमाणे 78pt मध्ये नऊ 5d इलेक्ट्रॉन व 1s ते 5p असे ६८ इलेक्ट्रॉन अधिक एक 6s इलेक्ट्रॉन. 78pt पेक्षा 79Au मध्ये अधिक एक 5d इलेक्ट्रॉन 80Hg मध्ये अधिक एक 6s इलेक्ट्रॉन, बाकीचे79Au प्रमाणे. याप्रमाणे सर्व कोष्टक वाचता येईल.
तरंगयामिकी आणि आणवीय प्रतिमान : प्रत्येक कणाला त्याच्या संवेगाला (वस्तुमान आणि वेग यांच्या गुणाकाराला) अनुरूप अशी तरंगलांबी असते, असे गृहीत फ्रेंच शास्त्रज्ञ द ब्रॉग्ली यांनी १९२४ मध्ये
अणूमधील इलेक्ट्रॉनांची कवचरचना. दिलेला अणूभार कार्बन (१२) बरोबर १२u प्रमाणे
|
अनुक्रमांक |
मूलद्रव्य व अणुभार |
K |
L |
M |
N |
|||||||||||||
|
n, 1 1, 0 1s |
2, 0 2s |
2, 1 2p |
3, 0 3s |
3, 1 3p |
3, 2 3d |
4,0 4s |
4, 1 4p |
|||||||||||
|
1 2 |
H(1·0080) He(4·003) |
1 2 |
. . |
. . |
. . |
. . |
. . |
. . |
. . |
|||||||||
|
3 4 5 6 7 8 9 10 |
Li(6·939) Be(9·012) B(10·81) C(12·000) N(14·007) O(15·999) F(18·998) Ne(20·183) |
2 2 2 2 2 2 2 2 |
1 2 2 2 2 2 2 2 |
. . 1 2 3 4 5 6 |
. . . . . . . . |
. . . . . . . . |
. . . . . . . . |
. . . . . . . . |
. . . . . . . . |
|||||||||
|
11 12 13 14 15 16 17 18 |
Na(22·990) Mg(24·312) Al(26·98) Si(28·08) P(30·974) S(32·064) C1(35·453) Ar(39·948) |
सर्व निऑन (Ne) प्रमाणे |
1 2 2 2 2 2 2 2 |
. . 1 2 3 4 5 6 |
. . . . . . . . |
. . . . . . . . |
. . . . . . . . |
|||||||||||
|
19 20 21 22 23 24 25 |
K(39·102) Ca(40·08) Sc(44·96) Ti(47·90) V(50·94) Cr(51·996) Mn(54·94 |
सर्व आर्गॉन (Ar) प्रमाणे |
. . 1 2 3 5 5 |
1 2 2 2 2 1 2 |
. . . . . . . |
|||||||||||||
|
अनुक्रमांक |
मूलद्रव्य व अणुभार |
K |
L |
M |
N |
O |
||||||||||||
|
1,0 1s |
2,0 2s |
2, 1 2p |
3,0 3s |
3,1 3p |
3,2 3d |
4,0 4s |
4, 1 4p |
4,2 4d |
4,3 4f |
5,0 5s |
5,1 5p |
|||||||
|
26 27 28 29 30 31 32 33 34 35 36 |
Fe(55·80) Co(58·93) Ni(58·71) Cu(63·54) Zn(65·37) Ga(69·72) Ge(72·59) As(74·92) Se(78·96) Br(79·91) Kr(83·80) |
सर्व आर्गॉन(Ar) प्रमाणे |
6 7 8 10 10 10 10 10 10 10 10 |
2 2 2 1 2 2 2 2 2 2 2 |
. . . . . 1 2 3 4 5 6 |
. . . . . . . . . . . |
. . . . . . . . . . . |
. . . . . . . . . . . |
. . . . . . . . . . . |
|||||||||
|
37 38 39 40 41 |
Rb(85·47) Sr(87·68) Y (88·90) Zr (91·22) Nb (92·91) |
सर्व क्रिप्टॉन(Kr) प्रमाणे |
. . 1 2 4 |
. . . . . |
1 2 2 2 1 |
. . . . . |
||||||||||||
अणूंमधील इलेक्ट्रॉनांची कवचरचना-पुढे चालू
|
अनुक्रमांक |
मूलद्रव्य व अणुभार |
K |
L |
M |
N |
O |
||||||||||||||||
|
1, 0 1s |
2, 0 2s |
2, 1 2p |
3, 0 3s |
3, 0 3p |
3, 2 3d |
4, 0 4s |
4, 1 4p |
4, 2 4d |
4, 3 4f |
5, 0 5s |
5, 1 5p |
|||||||||||
|
42 43 44 45 46 |
Mo(95·94) Tc(99·00) Ru (101·1) Rh(102·91) Pd (106·4) |
सर्व क्रिप्टॉन(Kr) प्रमाणे |
5 5 7 8 10 |
. . . . . |
1 2 1 1 . |
. . . . . |
||||||||||||||||
|
47 48 49 50 51 52 53 54 |
Ag(107·870) Cd(112·40) In(114·82) Sn(118·69) Sb(121·75) Te(127·60) I(126·90) Xe(131·3) |
सर्व पॅलॅडियम(Pd) प्रमाणे |
1 2 2 2 2 2 2 2 |
. . 1 2 3 4 5 6 |
||||||||||||||||||
|
अनुक्रमांक |
मूलद्रव्य व अणुभार |
K, L, M, N |
N |
O |
P |
|||||||||||||||||
|
1s ते 4d |
4, 3 4f |
5, 0 5s |
5, 1 5p |
5, 2 5d |
5, 3 5f |
6, 0 6s |
6, 1 6p |
6, 2 6d |
||||||||||||||
|
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
Cs(132·90) Ba(137·34) La(138·91) Ce(140·12) Pr(140·91) Nd(144·24) Pm(145·00) Sm(150·35) Eu(151·96) Gd(157·25) Tb(158·92) Dy (162·50) Ho (164·98) Er (167·2) Tm (168·93) Yb (173·04) Lu (174·97) |
1s ते 4d या कवकांमध्ये क्रिप्टॉन(Kr)प्रमाणेच४६ इलेक्ट्रॉन आहेत |
· . . 1 3 4 5 6 7 8 9 10 11 12 13 14 14 |
5s ते 5pमध्ये पॅलॅडियम(Pd) प्रमाणे 7 इलेक्ट्रॉन आहेच |
. . 1 1 . . . . . 1 . . . . . . 1 |
. . . . . . . . . . . . . . . . . |
1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
. . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . |
|||||||||||||
|
72 73 74 75 76 77 78 79 80 |
Hf (178·5) Ta (180·92) W (183·92) Re (186·2) Os (190·2) Ir (192.2) Pt (195·02) Au (196·97) Hg (200·59) |
1s ते 5p पर्यंत ६८ इलेक्ट्रॉन ल्युटेशियम (Lu) प्रमाणे आहेत. |
2 3 4 5 6 7 9 10 10 |
. . . . . . . . .
|
2 2 2 2 2 2 1 1 2 |
. . . . . . . . . |
. . . . . . . . . |
|||||||||||||||
अणूंमधील इलेक्ट्रॉनांची कवचरचना·पुढे चालू
|
अणुक्रमांक |
मूलद्रव्य व अणुभार |
K, L, M, N, O |
O |
P |
Q |
||
|
1s ते 5d |
5, 3 5f |
6, 0 6s |
6, 1 6p |
6, 2 6d |
7, 0 7s |
||
|
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
Ti (204·37) Pb (207·19) Bi (208·98) Po (210) At (210) Rn (222) Fr (223) Ra (226·01) Ac (227) Th (232·04) Pa (231) U (238·03) Np (237) Pu (242) Am (243) Cm (245) Bk (245) Cf (248) Es (253) Fm (254) Md (256) No (257) Lw(257,258) |
1s ते 5dमध्ये पाऱ्या(Hg) प्रमाणे७८ इलेक्ट्रॉन आहेत. |
. . . . . . . . . . 2 3 4 6 7 7 8 10 11 12 13 14 14 |
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
1 2 3 4 5 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 |
. . . . . . . . 1 2 1 1 1 . . 1 1 . . . . . 1 |
. . . . . . 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
मांडले ही तरंगलांबी λ = h / p या सूत्राने मिळते. (h = प्लांक- स्थिरांक p=संवेग) म्हणजे आणवीय इलेक्ट्रॉनांना ही तरंगलांबी असते. जितका वेग (किंवा ऊर्जा) अधिक तितकी तरंगलांबी लहान. उदा., १ ev (इलेक्ट्रॉन व्होल्ट म्हणजे १ व्होल्ट विद्युत् दाबाखाली प्रवेगित केलेल्या इलेक्ट्रॉनाची ऊर्जा) ऊर्जा असलेल्या इलेक्ट्रॉनाची तरंगलांबी १२·२३ A0. १० ev इलेक्ट्रॉनाची २·८७ A0 तर १ Mev (मिलियन—दशलक्ष — इलेक्ट्रॉन व्होल्ट) इलेक्ट्रॉनाची ०·०१ A0 इतकी लहान असते.
आधुनिक संशोधनाप्रमाणे बोर यांचे प्रतिमान आणवीय संरचनेला लागू पडत नाही. १९२५–२६ मध्ये हायझेनबेर्क व श्रोडिंजर यांनी पुंजयामिकी आणि तरंगयामिकी यांची व पुढे १९२८ मध्ये डिरॅक यांनी पुंजयामिकीची प्रस्थापना केली. हायड्रोजन-अणूमधील इलेक्ट्रॉन तरंगरूपाचा मानणे ओघाने आले. इलेक्ट्रॉन-गती श्रोडिंजर यांच्या प्रसिद्ध तरंग समीकरणाने नियंत्रित होते ते समीकरण असे:

|
– |
ħ2 |
∇2 Ψ + V (r) ψ = E Ψ |
|
2m |
हे समीकरण सोडविण्यासाठी काही अटी संभाळाव्या लागतात आणि त्यामुळे आपोआपच n, ι, mι हे पुंजांक उपस्थित होतात. ψ याचा अर्थ काय, हे एक कोडे होते. प्रथमतः माक्स बॉर्न यांनी ।ψ।2 आणि इलेक्ट्रॉन विवक्षित स्थळी असण्याची संभाव्यता यांचा संबंध जोडला. ।ψ।2 म्हणजे इलेक्ट्रॉनाची त्या त्या स्थानी असणारी संभाव्य घनता होय. या सिद्धांतानुसार जरी हायड्रोजन-अणूच्या (आणि त्याचप्रमाणे इतर अणूंच्या) सर्व ज्ञात घटकांचे सुसूत्र व अधिक समाधानकारक असे विवरण करता येत असले, तरी आणवीय संरचना कशी असावी
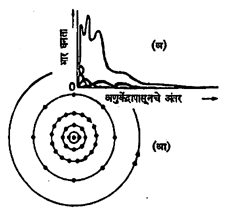
याचे चित्र डोळ्यापुढे येत नाही. आधुनिक सैद्धांतिक शास्त्रज्ञांच्या मते असे चित्र कल्पिणे निरर्थक व फोल आहे. कवच व कक्षा यांच्या भाषेत संरचनेचे वर्णन करणे सोयीचे असते. नवीन यामिकीप्रमाणे इलेक्ट्रॉनाच्या विद्युत् भाराचा विनिमय अशा प्रकारे होतो की, त्याचे कवचरूपाशी पुष्कळ साम्य आढळते हे आ. ३ मधील रुबिडियम (क्रमांक ३७) च्या आणवीय संरचनेवरून स्पष्ट होईल. येथे नवीन प्रतिमान हे आलेखाच्या रुपात दर्शविले आहे आणि जुनी पद्धतही कक्षांच्या रूपात दर्शविली आहे. प्रमुख पुंजांक १, २, ३, ४, ५ ला अनुरूप K, L, M, N, O च्या कवचांची अंतरे आणि विद्युत् भार घनतेच्या कमाल मूल्यांची केंद्रापासूनची अंतरे जुळली आहेत. म्हणजे नवीन पद्धतीमध्ये कवचरचना अध्याहृत आहे. हायड्रोजनामधील इलेक्ट्रॉन-घनतेची तरंगयामिकीप्रमाणे मिळणारी चित्रे आ. ४ मध्ये दर्शविली आहेत.
जवळजवळ पूर्ण एकवर्णी व तीव्र अशी लेसरची किरणशलाका आपाती प्रकाश म्हणून वापरल्यास रामन परिणामातील प्रकीर्ण रेषांच्या बाह्यरेखा अचूकतेने मोजता येतात. याखेरीज अणुशलाकांचा उपयोग करून होत असलेले अन्वेषण, रासायनिक विश्लेषणामुळे प्राप्त झालेला वर्णपटांचा अभ्यास इत्यादींमुळे आणवीय संरचनेसंबंधीच्या ज्ञानात अधिक भर पडत आहे.
संदर्भ : 1. Born, M. Tr. Fisher, J. W. The Mechanics of the Atom, New York, 1960.
2. Ruark, A. E. Atoms, Molecules and Quanta, Vol. I, New York, 1964.
गोडबोले, रा. द.
“