अनंत – १

अनंत – १ : गणितातील व तर्कशास्त्रातील त्याचप्रमाणे तत्त्वमीमांसेतील एक महत्त्वाची संकल्पना. गणितात आणि तर्कशास्त्रात या संकल्पनेला देण्यात आलेले अर्थ आणि संबंधित प्रश्न ह्यांचे विविचेन येथे प्रथम करण्यात आलेले आहे. त्यानंतर धर्मशास्त्र आणि तत्त्वमीमांसा यांमध्ये या संकल्पनेचे करण्यात आलेले विविध अर्थ आणि त्यांमधून निर्माण होणारे प्रश्न यांचे विविरण केलेले आहे.

 गणित आणि तर्कशास्त्र ह्यांमधील ‘अनंत’ ही संकल्पना : अंनत म्हणजे अंत नसलेला. सामान्य व्यवहारात ज्याची गणती करणे अशक्यप्राय असते किंवा ज्याच्या वाढीला किंवा विस्ताराला शेवट नाही त्याला आपण ‘अनंत’ म्हणतो. पूर्णांक (१,२,३….अशा संख्या) किती आहेत ? या प्रश्नाचे उत्तर ‘अनंत आहेत’ असे आपण चटकन देतो, कारण कितीही मोठी संख्या घेतली तरी तिच्या वरचढ मोठी संख्या असतेच व सर्वांत मोठी संख्या सांगणे केवळ अशक्य होय. तसेच सरळ रेषा कितीही वाढविली तरी ती संपत नाही. दोन समांतर रेषा कितीही वाढविल्या तरी एकमेकींस मिळत नाहीत म्हणजेच ‘त्यांचा छेदनबिंदू अनंतस्थ आहे’ असे म्हणतात. पण एखादी संख्या खूपमोठी आहे एवढ्यावरून ‘ती अनंत आहेत’ असे म्हणता येणार नाही. जसे समुद्रकिनाऱ्यावरील वाळूचे कण किंवा रात्री आकाशात दिसणारे तारे हे अनंत (म्हणजे मोजण्यास जवळजवळ अशक्य) आहेत असे सामान्यपणे म्हटले जाते तरी ते तत्त्वत: अनंत नाहीत.

गणितीय अनंत दोन प्रकारचे आहेत. एक संख्याविषयक व दुसरा अवकाशविषयक. पूर्णांकांचे असंख्यत्व आणि सरळ रेषा व प्रतल (पातळी) यांचा अमर्याद विस्तार यांवरून ‘अनंत’ या संकल्पनेचा उगम झाला असावा. बीजगणितात, जर य ≠ ० असेल तरच ^क्ष/_य या गुणोत्तराची व्याख्या होऊ शकते. गणितामध्ये शून्याने भागणे हे कृत्य नाही. आता ^क्ष/_य या गुणोत्तरातील क्ष स्थिर ठेवून जर य अधिकाधिक लहान होत होत शून्याच्या अगदी जवळ जात असेल तर गुणोत्तराचे मूल्य अधिकाधिक मोठे होत जाईल. या अमर्याद वाढीलाच ‘अनंताप्रत जाणे’ असे म्हणतात. हेच, जर य → ० तर ^क्ष/_य↔∞असे लिहितात.अनंताकरिता ∞हे चिन्ह आंग्ल गणितज्ञ वॉलिस (१६१६-१७०३) यांनी प्रथम वापरले. यात ∞ही संख्या नसून अनंतत्व दर्शविणारे चिन्ह होय.कलन व गणितीय विश्लेषण यांत अनंत व अत्यल्प या संकल्पना आधारभूत मानल्या जातात.

‘अनंत’ या संकल्पनेचा उद्गम व विकास : प्राचीन कालापासून तत्त्ववेत्ते, धार्मिक नेते व गणितज्ञ यांनी अनंताबद्दल मूलग्राही विचार केलेला आहे. भारतीय गणितात दशमान गणनपद्धतीत १०^१९ पर्यंतच्या संख्यांचा उल्लेख आहे पण अनंताचा संख्याविषयक विचार नाही, मात्र अनंताचा वस्तुगुणात्मक विचार आढळतो.

उपनिषदांतील ‘पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्यते’ यातील पूर्ण व गणितीय अनंत यांत साम्य दिसते. पदार्थाच्या अप्रतिहत अणुविभागणीवरून गणितीय अत्यल्प संख्येची संकल्पना डीमॉक्रिटस या ग्रीक तत्त्वज्ञाने इ.स.पू. ५व्या शतकात मांडली. या संकल्पनेचा प्रभाव १९व्या शतकापर्यंत गणितात दृढ होता. त्याच सुमारास ग्रीसमध्ये झीनो (इ. स. पू. ४९०-४३०) या तर्कशास्त्रज्ञाने अनंतासंबंधीचे महत्त्वाचे कूट प्रश्न त्याच्या प्रसिद्ध गतिविषयक विरोधाभासांच्या स्वरूपात मांडले व अनंतासंबंधीच्या तत्कालीन विचारांना धक्का देऊन त्यासंबंधीच्या मूलभूत प्रश्नांना चालना दिली. झीनोचे कूटप्रश्न पुढीलप्रमाणे आहेत : (१) द्विभाजन : गतिमान वस्तू काहीही अंतर जाण्यापूर्वी ती अर्धे अंतर गेली पाहिजे. हे अर्धे अंतर जाण्यापूर्वी त्याचे अर्धे अंतर ती गेली पाहिजे व असे अनंत काळपर्यंत होत असल्यामुळे गती अशक्य आहे, असे सिद्ध होते. (२) ससा व कासव यांच्या शर्यतीत, कासव आरंभी काही अंतर पुढे असल्यास ससा कासवास अनंत काळपर्यंत गाठू शकणार नाही. कारण कासव ज्या ठिकाणी आहे त्या ठिकाणी ससा येईल तेव्हा कासव ते स्थान सोडून पुढे गेलेले असेल व या विचारमालिकेनुसार कासव नेहमी सशाच्या पुढेच राहील. म्हणजेच ससा कासवास गाठू शकणार नाही. (३) गतिमान बाण हा प्रत्येक क्षणी पुढे सरकत असतो, परंतु अवकाशात प्रत्येक क्षणी तो कुठे तरी असतो. गतिमान म्हणजे कुठल्याही क्षणी कुठेही एका ठिकाणी नसणे, असे मानल्यास असा बाण हलू शकत नाही असे सिद्ध होते.

झीनोने विरोधाभासांच्या स्वरूपात गणितीय अत्यल्प, अनंत व सांतत्य या संकल्पनांतील मूलभूत अडचणी परिणामकारक पद्धतीने मांडल्या आहेत. ॲरिस्टॉटलपासून अनेक तत्त्ववेत्त्यांनी या कूटप्रश्नांची उकल करण्याचे प्रयत्न केले पण ते अयशस्वी ठरले. शेवटी १९व्या शतकाच्या उत्तरार्धात व्हायरश्ट्रास, डेडेकिंट व कँटर या तीन जर्मन गणितज्ञांनी या कूटप्रश्नांची कायमची व निर्णायक उकल करून दाखविली व गणितीय अनंताला आधुनिक स्वरूप दिले. व्हायरश्ट्रास यांनी अत्यल्पाचे उच्चाटन करून कलनशास्त्रातील ‘तत्क्षणिक वेग’ या संकल्पनेच्या साहाय्याने असे दाखवून दिले की, गतिमान बाण तत्क्षणी खरोखर स्थिर असला तरी कालावधीत तो स्थित्यंतर करीत असल्याने गतिमानता व स्थिरत्व यांच्यात मूलत: परस्परविरोध नाही. चलच्चित्रपटावरून याची यथार्थता सहज पटेल. द्विभाजन व ससा-कासव यांसंबंधीचे विरोधाभासही अभिसारी अनंत श्रेढीच्या [→श्रेढी]सिद्धांतावरून उकलता येतात. अभिसारी अनंत श्रेढीत असंख्य पदे असली तरी त्यांची बेरीज बंधित (मर्यादा असलेली) असते असे सीमा-पद्धतीने दाखविता येते. यामुळेच ससा व कासव यांच्यामधील अंतर जरी अनंत लहान-लहान अंतरालांच्या युतीमुळे बनत असले तरी ते बंधित असते व ससा ते बंधित कलावधीत गाठू शकतो. अनंत संचाची व गणितीय सांतत्याची यथार्थ कल्पना न आल्यामुळे आतापर्यंत हे कूट प्रश्न संपूर्णपणे अनुत्तरीत राहिले होते. पूर्वीचे तत्त्वज्ञ व गणितज्ञ झीनोच्या कूट प्रश्नांतील गृहीतके स्वीकारीत परंतु त्यावरून सरळ तर्काने निघणारे निष्कर्ष मात्र नाकारीत होते व ही त्यांची मूलभूत चूक होती. कँटर यांनी त्यांतील गृहीतके झुगारून दिली व त्यामुळे चमत्कारिक निष्कर्ष स्वीकारण्याची आवश्यकता राहिली नाही (याचा उल्लेख पुढे आला आहे). डेडेकिंट यांनी सुक्रमतेचे गृहीतक [→संच सिद्धांत] वापरून परिमेय संख्यांच्या (पूर्णांकांच्या गुणोत्तराच्या स्वरूपात मांडता येतात अशा संख्यांच्या) द्विभाजन-पद्धतीने अपिरमेय संख्यांचे गणितीय अस्तित्व सिद्ध करण्याची पद्धती शोधून काढली व सत् संख्याच्या संचाचे (परिमेय व अपरिमेय संख्या मिळून होणारा संच, →संख्या) सांतत्य तर्कशुद्ध व अंकगणितीय स्वरूपात (भूमितीय संकल्पनांपासून संपूर्ण मुक्त) प्रस्थापित केले.

कँटर अनंत-सिद्धांत : १९व्या शतकाच्या उत्तरार्धात कॅंटर यांनी गणितशास्त्रातील महत्त्वाचा असा संच सिद्धांत मांडला. आतापर्यंत संचातील वस्तुसंख्या एकामागून एक मोजून क्रमसूचक रीतीने निश्चित करण्याची पद्धती होती. परंतु कँटर यांनी दोन संचांचे तुल्यत्व, त्यांतील घटक-वस्तूंच्या परस्पर एकास-एक संवादावरून निश्चित करण्याची संकल्पना मांडली. या रीतीने दोन समसंख्या सांत संचांचे तुल्यत्व त्यांतील घटकांच्या जोड्या लावून ठरविता येईल. यात मूळ क्रिया वस्तू मोजणे ही नसून त्यांच्या जोड्या लावणे ही आहे. उदा., एका हाताची बोटे व पंचपात्रातील पाच भांडी यांचा एकास-एक संवाद असल्याने दोन्हींची संख्या एकच आहे. पाच हा अशा समसंख्य संचांचां संचांक आहे, असे कँटर म्हणतात. यावरून सांत (मर्यादा असलेल्या) संख्या संचात अंतर्भूत असलेल्या उपसंचाचा संचांक संचाच्या संचांकापेक्षा लहान असतो हे सहज समजेल. परंतु हीच गणनपद्धती पूर्णांकांच्या संचांना लावण्यापूर्वी कँटर यांना असे आढळून आले की, सांत गणितातील ‘वस्तूचा भाग वस्तूपेक्षा लहान असतो’ हे स्वयंसिद्धक (स्वसिद्ध तत्त्व) सोडून द्यावे लागते. विषमांक किंवा समांक हे धन संख्या-संचाचे भाग आहेत तरीही त्यांच्याच परस्पर एकास-एक संवाद दाखविता येतो. जसे

यामुळे नवीन व्याख्येनुसार वरील तिन्ही संचांचे संचांक एकच आहेत. याचा अर्थ पहिला अनंत संच त्याच्या पोटात असलेल्या बाकीच्या अनंत संचांशी तुल्य आहे. प या पूर्णांकावर अवलंबित असलेल्या फ (प) या फलनामुळे मिळाणार्‍या संचाशीही वरील संचाचा एकास-एक संवाद दाखविता येईल. यापुढे जाऊन कँटर यांनी परिमेय संख्या-संचाचाही पूर्णांक संचाशी एकास-एक संवाद आहे, असे कर्ण-पद्धतीने दाखविले. ज्या संचाचा धन पूर्णांक-संचाशी एकास-एक संवाद प्रस्थापित करता येतो, अशा संचास ‘गणनीय संच’ म्हणतात.

परंतु याही पुढे जाऊन कँटर यांनी असे दाखवून दिले की, सत्-संख्या-संच व परिमेय संख्या-संच यांमध्ये एकास एक संवाद असू शकत नाही. कारण असा संवाद प्रस्थापित करण्याच्या कोणत्याही प्रयत्नात अनेक संख्या निसटून जातात. त्यामुळे त्यांचा संचांक गणनीय संचांच्या संचांकांपेक्षा उच्च श्रेणीचा असला पाहिजे. सत् संख्यांच्या संचाला ‘सहतती’ (काँटिन्यूअम) असे म्हणतात व त्याच्या संचांकाला कँटर यांनी c हे चिन्ह दिलेले आहे. या संचांकांना ‘सांतातीत संख्या’ म्हणतात. सांतातीत संख्यांचे सुसंबद्ध गणितही कँटर यांनी बसविले व उच्च आणि उच्चतर श्रेणीच्या सांतातीत संख्यांचे अस्तित्व सिद्ध केले. सांत संख्यांशी केलेल्या गणितीय कृत्यांचा (उदा., बेरीज, गुणाकार इ.) त्यांच्यावर काहीही परिणाम होत नाही, पण सांतातीत संख्यांशी केलेल्या कृत्यांमुळे उच्चतर श्रेणीच्या सांतातीत संख्या निर्माण होऊ शकतात. गणनीय संचाच्या संचांकाला कँटर यांनी 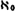 (अलेफ नल्) व सत् संख्यांच्या अगणनीय संचांकाला  अशी चिन्हे दिलेली आहेत. थोडक्यात हे गणित पुढीलप्रमाणे आहे :

गणितीय विश्लेषणशास्त्रातील अंनत : पहिल्या परिच्छेदात निर्देश केलेली अनंताची संकल्पना व∞ हे चिन्ह कलनशास्त्र आणि फलनविश्लेषणात मूलभूत महत्त्वाची आहेत. ग्रीक गणितात भूमितिपद्धतीमुळे व संख्या-गणन-पद्धतीच्या अभावामुळे अनंताची कल्पना अवकाशविषयक व गुणात्मक राहिली. पण पुढे मध्ययुगात भारतीय दशमान गणनपद्धतीचा अरबांमार्फत यूरोपात प्रचार झाल्यावर बीजगणित व अंकगणित यांची झपाट्याने वाढ झाली. १६व्या शतकात देकार्त यांनी बैजिक भूमितीचा पाया घातल्यानंतर १७व्या शतकात न्यूटन व लायप्निटस यांनी कलनशास्त्र निर्माण केले व त्याचबरोबर अनंत व अत्यल्प या संकल्पना पुन्हा पुढे आल्या. अवकलन व समाकलन यांत अनंत व अत्यल्प यांचा उपयोग मूलभूत आहे. परंतु १७व्या व १८व्या शतकात कलनशास्त्राची प्रचंड वृद्धी होऊनही अनंत व अत्यल्प या पायाभूत संकल्पनांचा सूक्ष्म विचार झाला नाही. १९व्या शतकाच्या आरंभी गौस व मुख्यत्वे कोशी या गणितज्ञांनी अवकलनाची [→अवकलन व समाकलन ]व्याख्या फलन-पध्दतीने सीमेच्या स्वरूपात मांडली आणि समाकलन हे अभिसारी अनंत श्रेढीची सीमा म्हणून प्रस्थापित केले, त्यामुळे या संकल्पना भूमितीच्या बंधनातून मुक्त झाल्या. तथापि अत्यल्पाच्या रूपाने अजूनही भूमितीय कल्पना शिल्लक होत्याच. शेवटी व्हायरश्ट्रास यांनी अत्यल्पाचे उच्चाटन करून संख्यांवर आधारलेल्या अंकगणितीय पध्दतीने फलन-सीमा व अभिसारी अनंत श्रेढीच्या सीमा यांच्या व्याख्या सरळ व सोप्या भाषेत मांडल्या. आधुनिक सत्-व असत्-फलन विश्लेषण,ðसंस्थितिविज्ञान,संभाव्यताशास्त्र, सांख्यिकी इ. शाखांत अनंत व अनंत-चिन्हाचा उपयोग सर्रास करण्यात येतो.

भूमितीतील अनंत : भूमितीतील सरळ रेषा ही अनंत बिंदूचा संच असते व या अनंत संचाचा संचांक सत् संख्यांच्या संचाइतकाच म्हणजेच c असतो. कारण दोहोंचा परस्पर एकास-एक संवाद प्रस्थापित करता येतो. विशेष म्हणजे बंधित रेषाखंडातील बिंदुसंच व अनंत रेषेतील बिंदुसंच यांचे संचांक एकच म्हणजे c आहेत. इतकेच नव्हे तर कँटर यांनी असेही सिद्ध केले की, अनंत विस्तृत प्रतल किंवा त्रिमित किंवा प-मित अवकाश यांच्या सर्व बिंदूच्या संच वरील संचाशी तुल्य असतो.

यूक्लिडीय प्रक्षेपीय भूमितीत [→भूमिती] एकदिश समांतर रेषांच्या कल्पित छेदनबिंदूस ‘अनंतस्थ बिंदू’ किंवा ‘आदर्श बिंदू’ म्हणतात. या सर्व बिंदूंच्या रेषेला  ‘अनंतस्थ रेषा’ म्हणतात. मात्र आदर्श बिंदू एकच व आदर्श रेषा एकच मानावयास हवी. यामुळे भूमितीतील बिंदू व रेषांचे छेदन-गुणधर्म निरपवाद वापरता येतात. याच पद्धतीने त्रिमित प्रक्षेपीय भूमितीत आदर्श अनंतस्थ प्रतल मानतात. प्रक्षेपीय भूमितीत समघात-सहनिर्देशकांच्यासाहाय्याने आदर्श बिंदू, रेषा व अनंतस्थ वर्तुळबिंदू यांचा उपयोग केला जातो.

गणितीय अनंताचे अस्तित्व : ‘गणितीय अनंताला अस्तित्व आहे: काय?’ या प्रश्नाचे उत्तर देण्यापूर्वी या प्रश्नाचा अर्थ आपण कसा लावावयाचा आणि त्याचे उत्तर शोधण्याकरिता कोणती रीत वापरावयाची, हे ठरवावयास हवे. गणितीय अनंत म्हणजे अनंत संच अस्तित्वात आहेत अशी कल्पना केल्यास, अशा संचांवर विसंगतींपासून मुक्त अशी गणितकृत्ये करता येतात की नाही, हे बघावयास हवे. अशी कृत्ये विसंगती निर्माण न होता करता येतात हे कँटर यांनी सांतातीत संख्या योजून दाखवून दिले आहे. त्याकरिता त्यांनी सांत संख्यांसंबंधीचे सामान्य सत्य—वस्तुसंचाचा अंश संपूर्ण संचापेक्षा लहान असतो —झुगारून देऊन दोन अनंत संचांची तुल्यता त्यांतील घटक वस्तूंच्या परस्पर एकास-एक संवादावर मानली. यात विसंगती नसून ते अनंत संचाचे भिन्नत्वदर्शक वैशिष्ट्य आहे. किंबहुना संचाची व्याख्याच कँटर व डेडेकिंट यांनी अशी केलेली आहे की, ‘जो संच आपल्या एका तरी अंतर्भूत उपसंचाशी तुल्य असतो तो अनंत संच होय.’ याच रीतीने सांतातील संख्यांच्या  कृत्य-गणितात विसंगती नाही असे दाखविता येते.

कँटर यांच्या अनंत संच सिद्धांतामध्ये, वरील व्याख्यामुळे निर्माण होऊ शकणारी एकही विसंगती अजूनपर्यंत दाखविली गेलेली नाही. सारांश, गणितीय अनंत ही कल्पना सुसंगत आहे आणि याचाच अर्थ तिला सांत संख्यांप्रमाणेच अस्तित्व आहे. या कल्पनेला रसेल—व्हाईटहेड मतप्रणालीप्रमाणे गृहीतकानुसारी तर्कशास्त्रीय अधिष्ठान आहे व म्हणून प्लेटोप्रमाणे आदर्श ‘आयडियां’च्या विश्वात या अनंताचे स्थान शोधण्याचे कारण नाही किंवा कांटप्रमाणे अवकाश आणि काल ह्यांचे आपल्याला जे साक्षात दर्शन होते त्यांच्या मध्येही या संकल्पनेचे अधिष्ठान शोधण्याचे कारण नाही.

कँटर-पद्धतीने अनंत-संचांचा व्यापक अभ्यास करताना रसेल यांना आढळून आलेला प्रसिद्ध ‘रसेल-विरोधाभास’ अनंत संचाच्या संदर्भात उल्लेखनीय वाटतो. प्रत्येक संच स्वत: आपल्या संचाचा सामान्यपणे घटक नसतो परंतु ‘सर्व संचांचा संच’ घेतल्यास ‘तो आपल्या संचाचा घटक आहे की नाही ?’ याचे उत्तर ‘आहे’व ‘नाही’ असे दोन्ही द्यावे लागते. हाच रसेल यांचा विरोधाभास होय व त्याचे निरसन रसेल-व्हाईटहेड यांनी प्रिन्सिपिया मॅथेमॅटिका या त्यांच्या सुप्रसिद्ध ग्रंथामध्ये तार्किक प्रकारांच्या साहाय्याने केले आहे [→गणिताचा तात्विक पाया]. अनंत संचांसंबंधी दुसरा अनुत्तिरित प्रश्न म्हणजे गणनीय संख्या-संचांक 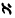आणि सत्‌संख्या संचांक c या दोहोंमध्ये असलेल्या संचांकाचा अनंत-संच आहे किंवा नाही याचा निर्णय अजून लागलेला नाही. यासंबंधी ‘नाही’ हे उत्तर गृहीत धरले आहे व त्या उत्तराशी अंतर्गत सुसंगतता कुर्ट गोडेल यांनी सिद्ध करून दाखविली आहे. (या संबधात उद्भूत होणारे ‘गणिताची अंतिम सुसंगता’ व तात्विक पायाभूत संकल्पना यासंबंधी सविस्तर विवेचनाकरिता ‘गणिताचा तात्विक पाया’ ही नोंद पहावी.)

अवकाश-गणितीय अनंत : जोपर्यंत यूक्लिडीय अवकाशच ज्ञात होते तोपर्यंत दृश्य विश्वही यूक्लिडीय, म्हणजे अनंत विस्तृत व शून्य वक्रतेचे असले पाहिजे, अशी सामान्य समजूत होती व तीच कांट यांच्या उपपत्तीय अभिप्रेत आहे. पण जेव्हा गणितार्थाने अयूक्लिडीय भूमितीचे अस्तित्वसिद्ध झाले तेव्हा ‘भौतिक अवकाशही अयूक्लिडीय असू शकेल’ ही कल्पना निघाली. यूक्लिडीय अवकाश अनंत आहे, कारण त्यातील सरळ रेषा अमर्यादपणे वाढविता येतात. रीमानीय गोल अवकाशबंधित पण अमर्याद आहे, कारण त्यातील अल्पांतरीय रेषा गुरुवृत्ताच्या परिघापेक्षा लहान म्हणून बंधित असतात. त्रिकोणाच्या तीन कोनांची बेरीज यूक्लिडीय भूमितीत दोन काटकोन, रीमानीय गोल भूमितीत दोन काटकोनांपेक्षा अधिक, लोबाचेव्हस्की व बोल्यॉई यांच्या अपास्त भूमितीत दोन काटकोनांपेक्षा कमी असते. यावरून अवकाशवक्राची व्याख्या ठरविल्यास वरील तिन्ही अवकाश अनुक्रमे शून्य वक्र, धन वक्र आणि ऋण वक्र मानता येतील. भौतिक विश्व सांत की अनंत, हे ठरविण्यासाठी त्याकडे बघण्याचा दृष्टिकोन ठरवून प्रत्यक्ष अवलोकनात वरील कसोट्या लाववयास पाहिजेत. आइन्स्टाइड यांच्या व्यापक सापेक्षता सिद्धांतानुसार गुरुत्वक्षेत्रात गुरुत्वाकर्षित द्रव्य असलेल्या ठिकाणी अवकाश धन वक्र असले पाहिजे, मात्र अवकाशमापन दृढ परिमाणाने करावयास हवे. तेव्हा स्थूलमानाने विश्वातील द्रव्यवितरण समरूप आहे व एकंदर विश्व स्थिर आहे असे मानल्यास, वरील गणितीय कसोट्यांवरून अवकाश बंधित पण अमर्याद व अचल धन वक्रतेचे असले पाहिजे. परंतु विश्व जर सतत अधिकाधिक वेगाने विस्तार पावत असेल तर ते तत्क्षणी अचल धन वक्रतेचे पण कालावधीत अनंतोपगामी जाणारे असे मानावे लागेल. तात्पर्य, अवकाश अनंत आहे की सांत आहे, या प्रश्नांचे उत्तर दृष्टिकोनावर व अनुमानित भौतिक आधारत्त्वांवर अवलंबून आहे. गणितशास्त्र या उत्तराच्या फक्त कसोट्या सांगू शकते. प्रयोगावरून सध्या तरी दोन्ही कल्पना दृश्य विश्वासंबंधी निष्कर्ष काढण्यास सारख्याच उपयुक्त आहेत.

पहा : अवकाश: संख्या.

देशपांडे, कृ.के.

पाश्चात्त्य तत्त्वज्ञानातील ‘अनंत’ ही संकल्पना : पाश्चात्त्य तत्त्वज्ञानात ‘अनंत’ ही संकल्पना दोन स्वरूपात आढळते: (१) ग्रीक तत्त्वज्ञानात तिला जो अर्थ देण्यात आला आहे, त्या स्वरूपात आणि (२) ख्रिस्ती आणि आधुनिक तत्त्वज्ञानात ती ज्या अर्थाने वापरण्यात येते, त्या स्वरूपात.

(१)ग्रीक तत्त्वज्ञानाच्या इतिहासात अनंत ही संकल्पना प्रथम ॲनॅक्सिमँडर (इ.स.पू. ६ वे शतक) ह्या तत्त्ववेत्याने मांडली. त्याच्या म्हणण्याप्रमाणे दृश्य विश्वाचे घटक असलेली विवक्षित स्वरूपाची मूलतत्त्वे (जल, वायू इ.) एका अनंत अशा द्रव्यातून उगम पावतात आणि त्याच्यात विलीन होतात. हे द्रव्य अनंत असते ह्या म्हणण्याचा मुख्य अर्थ असा की त्याचे स्वरूप अमर्यादित ‘निर्विशेष’ असते पस्परविरोधी स्वरूपाची विविक्षित तत्त्वे त्याच्यातून उदयाला येत असल्यामुळे, ह्या मूलद्रव्याचे स्वत:चे स्वरूप विविक्षित असू शकत नाही. विचाराचे हेच सूत्र पकडून पायथॅगोरस याने वस्तूच्या मूळच्या ‘अमर्यादित’ अनंत प्रकृतीली परिमित व म्हणून निश्चित, सुव्यवस्थित स्वरूप प्राप्त करून देणारे, ‘सीमा’ असे एक तत्त्व आहे, असे कल्पिले. सीमा हे रचनेचे, व्यवस्थेचे तत्त्व आहे आणि वस्तू सुरचित, सुव्यवस्थित असली, तर ती चांगली, शोभन असते. म्हणन सीमित वस्तू चांगली असते असे असण्यात वस्तूचे कल्याण असते. प्लेटोनेही रचनेचे, व्यवस्थेचे, नियमनाचे सीमा हे तत्त्व आणि त्याला विरोधी असलेले असीम असे द्रव्य हे द्वंद स्वीकारले. प्लेटोने ह्या द्वंद्वाचा वेगवेगळ्या रीतींनी अर्थ लावला आहे. उदा., विवक्षित वस्तू, केवळ व्यक्ती ही असीम द्रव्यात मोडते. परंतु तिचे बुद्धिग्राह्य स्वरूप, ज्याच्यामुळे ती एका प्रकारची वस्तू असते ते, सीमेच्या तत्त्वाला अनुसरणारे असते. नैतिक क्षेत्रात माणसाची सुखाची वासना असीम द्रव्यात मोडते परंतु सीमेच्या तत्त्वापासून निष्पन्न होणाऱ्या नैतिक नियमांनी ह्या इच्छांचे नियमन होणे आवश्यक असते. सारांश, ग्रीक तत्त्वज्ञानात अनंत ही संकल्पना ‘अमर्यादित, निर्विशेष, निराकार असे द्रव्य’ ह्या अर्थाने वापरतात. उलट रूप, आकार नेहमी सीमित व सान्त असतो. ह्याचा अर्थ असा, की अनंत असणे ही श्रेयस्कर गोष्ट नव्हे. जे द्रव्य स्वत: सुव्यवस्थिच असू शकत नाही आणि सुव्यवस्थित व म्हणून श्रेयस्कर, स्वरूप प्राप्त होण्यासाठी ज्याला स्वत:हून वेगळ्या अशा सीमेच्या तत्त्वाची अपेक्षा असते, असे द्रव्य म्हणजे अनंत द्रव्य. उदा., ईश्वराला अनंत हे विशेषण लावता येणार नाही. प्लेटोच्या तत्त्वज्ञानात ईश्वराचे स्वरूप सीमेच्या तत्त्वाचा आदर करणारा आणि ह्या तत्त्वाला अनुसरून अव्यवस्थित, अनंत द्रव्यापासून सुव्यस्थित विश्वाची रचना करणारा विधाता, असे आहे. अनंत द्रव्य ईश्वराला परके आहे मर्यादा, सीमा हे तत्त्व ईश्वराला समीप, त्याच्याशी सरूप आहे.

(२)ख्रिस्ती तसेच आधुनिक तत्त्वज्ञानात अनंत ह्या संकल्पनेला वेगळा अर्थ देण्यात आला आहे. ज्या वस्तूचे अस्तित्व इतर वस्तूंकडून मर्यादित झालेले असते, अशी वस्तू म्हणजे सान्त वस्तू. सान्त वस्तूचे अस्तित्व दोन रीतींनी मर्यादित झालेले असते. एक तर तिचे अस्तित्व अन्य वस्तूच्या अस्तित्वावर अवलंबून असते आणि ह्या अर्थाने ते मर्यादित असते. दुसरे असे, की अन्य वस्तूंना अस्तित्व असल्यामुळेही सान्त वस्तूचे अस्तित्व मर्यादित असते. सान्त वस्तू म्हणजे केवळ एका प्रकारचे अस्तित्व. त्याहून अस्तित्वाचे अन्य प्रकार असल्यामुळे तिचे अस्तित्व ह्या इतर प्रकारच्या अस्तित्वांनी मर्यादित असते. उलट अनंत अस्तित्व हे संपूर्णपणे स्वावलंबी, स्वायत्त, स्वाधिष्ठित असते व इतर अस्तित्वे त्याच्यावर अवलंबून असतात. म्हणून ते इतर अस्तित्वांकडून मर्यादित नसते. शिवाय ते अस्तित्वाचा एक प्रकार नसते, तर अस्तित्वाच्या सर्व शक्यता अनंत अस्तित्वात नि:शेषपणे व्यक्त, फलद्रूप झालेल्या असतात. असे अनंत अस्तित्व म्हणजे ईश्वर किंवा कैवल्य. अनंत अस्तित्व आणि सान्त अस्तित्व ह्यांच्या परस्परसंबंध कसा लावावयाचा, हा मध्ययुगीन व आधुनिक तत्त्वज्ञानातील एक कूट प्रश्न आहे. ह्या प्रश्नाला दोन प्रकारची उत्तरे मिळतात. एक अंतर्शायीवादी. ह्या विचारसरणीप्रमाणे विश्वातील प्रत्येक वस्तू जरी सान्त असली, तरी ह्या वस्तूंचा संपूर्ण समूह किंवा संपूर्ण व्यवस्था ही एका स्वायत्त, परिपूर्ण अशा तत्त्वाचा आविष्कार आहे. हे स्वायत्त (म्हणून अनंत) अस्तित्व ज्याच्यात नि:शेषपणे आविष्कृत झाले आहे, असे हे विश्व अनंत आहे. हे विश्व सान्त आहे आणि अनंत अस्तित्व त्याच्या पलीकडे आहे, असे नव्हे. विश्व हे अनंत तत्वाची केवळ अभिव्यक्ती आहे, पण विश्वरूपाने व्यक्त झाल्याशिवाय अनंत अस्तित्व राहू शकत नाही व म्हणून अनंत व सान्त वस्तू परस्परावलंबी आहेत. स्पिनोझा (१६३२-१६७७) व हेगेल (१७७०-१८३१) ह्या तत्त्ववेत्यांनी हा दृष्टिकोन स्वीकारला आहे तथापि ह्या तत्त्वेवेत्त्वांच्या भूमिकांत महत्त्वाचे भेदही आहेत. दुसऱ्या प्रकारचे उत्तर म्हणजे अतिशायीवादी उत्तर. ह्या भूमिकेप्रमाणे विश्व सान्त आहे आणि स्वत: पलीकडल्या अनंत अस्तित्वावर सर्वस्वी अवलंबून आहे. उलट सान्त विश्वापलीकडचे हे अनंत तत्त्व संपूर्णपणे स्वायत्त आहे. विशेषत: खिस्ती धर्मशास्त्रज्ञांनी व त्यांच्यापासून स्फूर्ती घेतलेल्या तत्त्ववेत्यांनी ही भूमिका स्वीकारली आहे. अनंत अस्तित्वात अपेक्षित असलेली परिपूर्णता आणि विश्वाची अपूर्णता ह्यांच्यात सुसंगती कशी साधायची, ही अंतर्शायीवादातील प्रमुख अडचण आहे. अतिशायितावादाची अडचण वेगळी आहे. सान्त वस्तूंच्या सर्वस्वी पलीकडचे असे अस्तित्व अनाकलनीय ठरणार. कारण ज्या संकल्पनांच्या साहाय्याने आपण त्याचे आकलन करू पाहू, त्या सान्त वस्तूंना अनरूप असल्यामुळे अनंत तत्त्वाला लावता येणार नाहीत. म्हणून सर्वस्वी अनाकलनीय असे अनंत तत्त्व असून नसल्यासारखे होईल. विश्वाचे स्वरूप समजून घेताना ह्या तत्त्वाचे प्रयोजन उरणार नाही.

हे विश्व म्हणजे इंद्रियगोचर वस्तूंचा समूह किंवा मालिका एवढेच जे तत्त्ववेते मानतात, त्यांच्या दृष्टीने अनंत ही संकल्पना अवकाश, काल, संख्या इत्यादींच्या स्वरूपाचे वर्णन करतानाच काय ती आवश्यक असते. अनंताची ही संकल्पना म्हणजे गणितात जिचे विश्लेषण व निरूपण करतात ती संकल्पना होय.

रेगे, मे. पुं.

भारतीय तत्त्वज्ञानातील ‘अनंत’ ही संकल्पना : भारतीय तत्त्वाज्ञानातील अनंत संकल्पना प्रथम उपनिषदांत आली आहे. तैत्तिरीय उपनिषदात ब्रह्याचे स्वरूप ‘सत्यं ज्ञानं अनन्तं ब्रह्म’ ब्रह्म हे सत्य, ज्ञान व अनंत होय अशा प्रकारे वर्णिले आहे. ‘छांदोग्य उपनिषदात’ ‘अनंत’ पदाचा पर्यायशब्द ‘भूमा’हा सांगितला आहे, असे शंकराचार्य म्हणतात. ‘भूमा’ची व्याख्या तेथे ‘यत्र नान्यद्विजानाति’- ‘जेथे एकाहून दुसरे असे जाणले जात नाही ते भूमा’ अशी केली आहे. म्हणजे घट, पट इ. वस्तूंचा भेद जेथे मावळतो अशी वस्तू. शकराचार्यानी ‘जी वस्तू कशापासूनही वेगळी नाही ती अनंत’ होय, अशी अनंताची व्याख्या केली आहे. ‘वेगळेपणा’ म्हणजेच अंत तो जेथे नाही ते अनंत.

शंकराचार्यानी देशत:, कालत: व वस्तूत: अशी ब्रह्माची त्रिविध अनंतता सांगितली आहे. आकाश नाही असा प्रदेशच नाही, म्हणून आकाश देशत: अनंत होय. परंतु आकाश हे कार्य आहे, ते उत्पन्न होते, म्हणून आकाशाला कालत: अनंतता नाही जे उत्पन्न होत नाही व नाशही पावत नाही, ते कालत: अनंत होय ब्रह्म असे अनंत आहे. ‘अ’ व ‘ब’ अशा दोन वस्तू आहेत असे म्हटले, तर ‘अ’ नव्हे तो ‘ब’ व ‘ब’ नव्हे तो ‘अ’ ‘अ’ला ‘ब’ने मर्यादा पडते व ‘अ’ ने ‘ब’ला मर्यादा पडते. ‘ब्रह्म’ ही एकच वस्तू आहे, अन्य सर्व मिथ्या आहे म्हणून ब्रह्म हे वस्तुत: अनंत होय.

‘अनंत’ शब्दाने व्यक्त होणारी देशत: अनंतता वैशेषिक दर्शनात ‘विभु’ या पदाने व्यक्त केली आहे. आकाश, काल, दिक् व आत्मा ही विभु द्रव्ये आहेत. विभु म्हणजे सर्व मूर्त द्रव्यांशी संयुक्त. याच दर्शनात नित्य व अनित्य असे द्रव्यांचे वर्ग पाडले आहेत. नित्य म्हणजे कालत: अनंत उत्पत्ती व विनाश नसलेले. परमाणू, आकाश, काल, दिक् व आत्मा हे नित्य होत.

हे वस्तुमात्र बोद्ध विनाशी व क्षणभंगुर मानतात. परंतु वस्तूंचा कार्यकारणभावाने निर्माण होणारा प्रवाह अनादी मानतात. ते निर्वाण म्हणजे मोक्ष नित्य मानतात.

संख्याविषयक अनंतता भारतीय तत्त्वज्ञानात ‘अगण्य’ वा ‘असंख्य’ शब्दांनी व्यक्त करतात. परंतु अनंत नामक संख्या भारतीयांच्या साहित्यात निर्दिष्ट केलेली आढळत नाही.

जैन तत्त्वज्ञानाप्रमाणे कर्मबंधातून मुक्त जीवाच्या ठिकाणी अनंतचतुष्ट्य (चार अनंतगुण) म्हणजे अनंत ज्ञान, अनंत दर्शन, अनंत सुख व अनंत वीर्य असे व्यक्त होतात. विविध कर्मबंध असेपर्यंत हे जीवाचे गुण आवृत म्हणजे झाकून गेलेले असतात.

जोशी, लक्ष्मणशास्त्री

संदर्भ : 1. Coplest on, Frederick, A History of Philosophy, vol. VII, London, 1963.

           2. Cornford, F. M. Principium Sapientia, Cambridge, 1952.

           3. Courant, R. Robbins, H. What is Mathematics, New York, 1961.

           4. Dantzig. T. Number the Language of Science, London, 1947.

           5. Farrer, A. M. Finite and Infinite London, 1943.

           6. Hack-forth, R. Plato’s Examination of Pleasure, Cambridge, 1945.

           7. Newman, J. R. World of Mathematics, Vol. II, New York 1956.

“