सांख्यिकीय भौतिकी

सांख्यिकीय भौतिकी : (सांख्यिकीय यामिकी). द्रव्याच्या (प्रणालीच्या) स्थूलमानीय गुणधर्मांचे विवरण, त्याच्या सूक्ष्ममानीय घटकांच्या गुणधर्मांच्या आधारावर करण्याचा प्रयत्न करणारी सैद्घांतिक भौतिकीची ही शाखा आहे. यात साधारणपणे घटकांची संख्या खूप मोठी असते आणि त्यांची अभिलक्षणे व अन्योन्य क्रिया ज्ञात आहेत असे गृहीत धरलेले असते. स्थूलमानीय द्रव्याचा साठा पूर्णपणे अणू किंवा रेणूंचा बनलेला असतो. रेणूंच्या रचनेच्या ज्ञानाचा आणि यामिकीच्या नियमांचा उपयोग करून स्थूलमानीय द्रव्याच्या साठ्याचा वर्तनाचे किंवा स्थूलमानीय प्रणालीच्या वर्तनाचे किंवा प्रवृत्तीचे अनुमान करण्याचे कार्य सांख्यिकीय भौतिकीत केले जाते. यासाठी गणिती आणि राश्यात्मक पद्घती वापरून स्थूलमानीय द्रव्याच्या साठ्याच्या वर्तनाचे किंवा प्रवृत्तीचे विवरण त्याचे घनफळ,घनता, दाब, तापमान इ. पदांमध्ये करण्यात येते.

घनफळ (V), वस्तुमान(m), ऊर्जा (E) असलेल्या एक-आणवीय निऑन वायूच्या अगदी साध्या ऊष्मागतिकीय प्रणालीचे उदाहरण पुढे दिले आहे.सांख्यिकीमध्ये m ऐवजी रेणूंची एकूण संख्या N या ऊष्मागतिकीय चलपदाचा उपयोग करतात.या साध्या प्रणालीची ऊष्मागतिकीय संतुलित अवस्था स्पष्ट करण्यासाठी V, E आणि N यांचा विनिर्देश पुरेसा होतो.या प्रणालीला विशिष्ट तापमान (T), दाब (P) आणि प्रतिअणू रासायनिक वर्चस्  म्यू(μ) असते.N ही खूप मोठी संख्या असते.रूढ पद्घतीत N  पैकी प्रत्येक अणू किंवा रेणूचे तीन कार्तीय सहनिर्देशक आणि त्याचा वेग किंवा संवेगाचे तीन सदिश घटक असे 6N सहनिर्देशक स्पष्ट करून अशा वायूच्या दिलेल्या क्षणकालाच्या सूक्ष्मावस्थेचे वर्णन केले जाते. प्रत्यक्षात सांख्यिकीय भौतिकीमध्ये हॅमिल्टोनिअन स्वरूपातील यामिकीचे नियम वापरण्याचा प्रघात आहे. त्यामुळे  तीन कार्तीय सहनिर्देशकाबरोबर संवेगाचे तीन सदिश घटक P_Xi = m_i v _xi P_yi = m_i V_yi   P_Z i वापरले जातात. याचा विशेष उपयोग जटिल प्रणालींचे गणिती संस्करण करताना होतो. 3N कार्तीय सहनिर्देशक आणि संवेगाचे 3N सदिश घटक यांच्या सहअस्तित्त्वास प्रणालीचा अवस्था-अवकाश किंवा गॅमा-अवकाश असे नाव आहे. याउलट, वायूतील एका रेणूचे तीन कार्तीय सहनिर्देशक आणि संवेगाचे तीन सदिश घटक यांच्या षट्मितीय अवस्था – अवकाशाला म्यू-अवकाश असे नाव आहे. द्वि-किंवा बहु- आणवीय रेणूंचे आंतरसहनिर्देशक आणि त्यांचे संयुग्मी संवेग घटक (यांना सामान्य संवेग म्हणतात आणि हे वर्चस् ऊर्जा आणि गतिज ऊर्जेशी संबंधित असतात) हेदेखील रेणूंच्या वस्तुमान केंद्राच्या तीन कार्तीय सहनिर्देशकांबरोबर वापरतात. गॅमा सहनिर्देशकांच्या एकूण संख्येला प्रणालीच्या मुक्तमात्रा म्हणतात. कोणत्याही t वेळेची वायूची सूक्ष्मावस्था गॅमा-अवकाशात एका बिंदूने किंवा म्यू-अवकाशात N बिंदूंनी (प्रत्येक अणू किंवा रेणूचा एक बिंदू याप्रमाणे) दाखविली जाते.म्यू-अवकाशातील एकूण सहनिर्देशकांची संख्या प्रतिरेणूमधील अणूंच्या संख्येच्या सहापट असते.

या विषयाची कल्पना येण्यासाठी प्रथम भौतिकीय वाद वा सिद्घांत म्हणजे काय याचा विचार करण्यात येतो.कोणत्याही भौतिकीय वाद अगर सिद्घांताचा परिपाक म्हणून काही विशिष्ट मूल्ये असलेली समीकरणे मिळतात. ही समीकरणे प्रत्यक्ष प्रयोगान्ती सार्थ ठरल्यास तो वाद वा सिद्घांत यशस्वी मानला जातो. भौतिकीय सिद्घांताच्या दोन महत्त्वाच्या शाखा गतिकी व यामिकी आणि सांख्यिकी यांची तुलना करता असे दिसून येते की,अनेक नैसर्गिक घटनांचा अर्थ लावण्यात गतिकी व यामिकीस चांगले यश लाभले आहे. परंतु गतिकी व यामिकीत निरपेक्ष निश्चयवाद अंगभूत आहे. सीमांत व प्रारंभिक अटी एकदा ठरल्या की, पुढील कोणत्याही क्षणी असणारी चलांची (उदा.,स्थिती व गती) मूल्ये गतिकी व यामिकीने परिशुद्घ रीत्या ठरविली जातात परंतु अनेक कणांचा बनलेल्या व गतिनियमानुरूप परस्परांच्या प्रेरणेखाली त्यांच्या हालचाली होत असलेल्या अशा एखाद्या वायूचा विचार याच  पद्घतीने केला, तर एका घन सेंटिमीटरमध्ये सामावलेल्या वायूच्या कणांची संख्या इतकी मोठी असते की, त्यातील प्रत्येक कणाची कोणत्याही क्षणी असलेली स्थिती व गती सांगणे अत्यंत कठीण किंबहुना अशक्यप्राय होईल आणि या दृष्टीने गतिकी व यामिकीचा विशेष उपयोग होऊ शकणार नाही. परंतु सांख्यिकी अशा परिस्थितीत उपयोगी येते. सांख्यिकीय पद्घतीत स्वतंत्र कणांचा विचार करीत नाहीत, तर विशिष्ट गुणधर्म (उदा.,स्थिती, गती, संवेग, ऊर्जा इ.) असलेल्या कणांच्या गटांचा विचार करतात. विशेष म्हणजे अशा गटातील कणांची संख्यादेखील परिमित न समजता ती सरासरी वा माध्य असते. सांख्यिकीय माध्यांचे गणित ⇨संभाव्यतेच्या कल्पनेवर आधारलेले आहे. ही संभाव्यतापदोपदी प्रत्ययास येते. विशेषतः अत्यंत काळजीपूर्वक केलेल्या प्रयोगांतहीराशींच्या मापनात संभाव्यता आपले अस्तित्व दाखविते. त्रुटीचावादसंभाव्यतेवर आधारलेला आहे. नैसर्गिक प्रकिया (उदा., उष्णतेचेसंवहन) सर्वस्वी अव्युत्क्रमी असतात व अशा घटनांचा विचार करण्याससांख्यिकीय पद्घती विशेषेकरून समर्थ आहे, याचे कारण त्या पद्घतीतमाध्य वितरणांचा उपयोग करतात व ही माध्ये वितरणांची संभाव्यतालक्षात घेऊन काढली जातात. ज्या वितरणांची संभाव्यता सर्वांत अधिकतीच वितरणे प्रत्यक्षात  आढळतील ही गोष्ट स्पष्ट आहे. काही बदलझालाच तर तो  वाढणाऱ्या संभाव्यतेच्या दिशेने होईल. असे आढळतेकी, उष्णतेचे संवहन नेहमी उच्च तापमानाकडून नीच तापमानाकडेहोते, कारण तसे होण्याची संभाव्यता उलट दिशेने होणाऱ्या उष्णतासंक्रमणाच्या  संभाव्यतेपेक्षा किती तरी पटीने मोठी असते. याचाच अर्थअसा की, होणारा बदल एकाच दिशेने होईल व म्हणून घडणारी प्रकियाअव्युत्क्रमी होईल. 

सांख्यिकीय भौतिकीमध्ये मुख्यतः एकच उद्देश असतो व तोम्हणजे समूहातील N सर्व सम गटांची त्यांच्या शक्य असलेल्या स्थितीतऊर्जेस अनुलक्षून विभागणी करावयाची. गटागटात  अन्योन्यक्रिया(परस्परक्रिया) असलीच तर ती इतकी मंद असल्याचे समजावयाचे कीती लक्षात घेण्याची जरूरी नाही. शिवाय प्रत्येक गटास व्यक्तिगत अशीऊर्जा असून या सर्व व्यक्तिगत ऊर्जांची बेरीज समूहाच्या ऊर्जेइतकी म्हणजे E असते. येथे ऊर्जेची भूमिका गतीचा स्थिरांक अशा तऱ्हेची आहे. ऊर्जेव्यतिरिक्त इतर गुण (उदा., संवेग परिबल) वितरण करतानाऊर्जेऐवजी वापरता येतील परंतु विशेषेकरून ऊष्मागतिकीत त्यास विशेषस्थान प्राप्त झालेले नाही. गटांचे प्रत्येक वितरण समूहाची शक्य असलेली स्थिती दर्शविते. 

---

दोन भिन्न विचार सरणींचा उल्लेख येथे केलेला आहे. पहिल्या व जुन्या विचारसरणीस मॅक्सवेल-बोल्टस्मान (मॅ.-बो.) सांख्यिकी असे नाव आहे. यासच ‘रूढ सांख्यिकी’ म्हणतात. याचा उपयोग मुख्यतः वायूंच्या रेणूंचा अगर प्लांक दोलकांच्या समूहाचा विचार करताना होतो. वायूतील रेणू एकमेकांपासून दूर असल्याने त्यांच्यात अन्योन्यक्रिया जवळजवळ नाहीच असे  धरून चालता येते परंतु घन पदार्थांत अणू अगर रेणू एकमेकांचे अत्यंत जवळ असल्याने त्यांच्यात अन्योन्यक्रिया व त्यामुळे उत्पन्न होणारी ऊर्जा असते. दुसऱ्या विचारसरणीचा उगम ⇨ जोसिआ विलर्ड गिब्ज यांच्यापासून झाला व या पद्घतीने कोणत्याहीभौतिकीय संहतीचा विचार करता येतो. प्रथम मॅक्सवेल-बोल्टस्मानसांख्यिकीची माहिती पुढे दिली आहे. 

मॅक्सवेल-बोल्टस्‌मान सांख्यिकी : अगोदर वर्णन केल्याप्रमाणे खूप संख्येने असलेल्या N वस्तू अगर कण (उदा., वायूचे रेणू) यांचा एक समूह आहे व त्यांच्याशी निगडित असलेल्या ऊर्जेस अनुलक्षून त्यांची विभागणी काही गटांत करावयाची आहे. वस्तू मुक्त व अप्रभेद्य आहेत आणि कोणतीही एक वस्तू एका गटामध्ये असण्याची जेवढी शक्यता आहे तेवढीच तिची दुसऱ्या गटामध्ये असण्याचीही शक्यता आहे. सर्व गटांना प्रत्येकी व्यक्तिगत संभाव्यता असून ती g₁, g₂, g₃,…, G_j ,…, g_m यांनी दर्शविली जाते. j गटातील वस्तुगणिक ऊर्जा E_j आहे व त्यातील वस्तूंची सरासरी संख्या N_j आहे. एकंदर वस्तूंची म्हणजे वस्तूंच्या समूहाची ऊर्जा ΡN_j E_j = E इतकी आहे व ती स्थिर राहते. वस्तूंची एकंदर संख्याही ( ΡNj =N) स्थिर राहते. वितरण अतिसंभवनीय असेल तर त्या वितरणाची संभाव्यता w महत्तम होईल. संभाव्यता दोन तऱ्हांनी मांडता येते. (१) अपूर्णांक स्वरूपातः एखाद्या नेमबाजाचा नेम १२ पैकी ९ वेळा बरोबर लागत असल्यास त्याच्या कोणत्याही नेमाच्या यशाची संभाव्याता ९/१२ अथवा ३/४ येईल व अपयशाची संभाव्यता १/४ येईल (२) पूर्णांक स्वरूपात : काही वेळेस जितक्या वेळेस यश मिळाले असेल ती संख्याच (वरील उदाहरणात ९) यशाची संभाव्यता दाखविण्याकडे वापरतात. पुढील सर्व विवेचनात ही दुसरी पद्घत अनुसरली आहे, म्हणजे w, g_j या पूर्ण संख्या आहेत. याप्रमाणे w चे मूल्य पुढीलप्रमाणे मांडता येते.

अथवा  थोडक्यात समी. १ असे होइल.

 

पळावयाच्या शर्ती खालीलप्रमाणे आहेत : 

w महत्तम असल्यास w चा लॉग घेऊन व δ हे अवकलन चिन्ह वापरून पुढील समीकरण असे मांडता येईल. 

δ लॉग_e W= 0… … … … … … … … … … (३) 

त्याचप्रमाणे समी. (२) पासून d ΣN_j Ej=0, d Ρ N_j =0 … (३ अ) ही समिकरणे मिळतात. 

    जेम्स स्टर्लिंग यांच्या सूत्राप्रमाणे,

लॉगN! = N लॉगN! −N+ लॉग 2π+१/२ लॉग N. 

यात N ही संख्या खूप मोठी असल्यास शेवटची दोन पदे तुलनेने अल्प असल्याने ती सोडता येतात. ती तशी सोडून देऊन व N ही संख्या खूप मोठी आहे हे लक्षात ठेवून स्टर्लिंग यांचे सूत्र असे होईल. 

      लॉग N! =N लॉग N–N … … … … … … … .. (४)

N मोठी संख्या असण्याची अट विचारात घेतलेल्या वस्तूंच्या समूहाच्याबाबतीत पूर्ण लागू पडते. परंतु j गटातील N_j संख्येबाबत, N_j लहान असल्यास लागू पडणार नाही ही गोष्ट खरी असली तरीही, समीकरण (४) प्रमाणे लॉग N_j! चे मूल्य लिहून जी काही चूक येईल, ती इतकी थोडी असेल की त्यामुळे एकंदर बेरजेत जाणवण्याइतका फरक पडणार नाही. म्हणून स्टर्लिंग सूत्र (समी. ४) वापरून समीकरण (३) व (३ अ) पासून अनुक्रमे

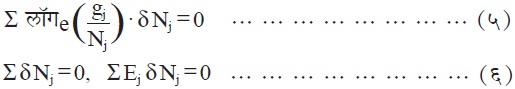
ही समीकरणे मिळतात.⇨झोझेफ ल्वी लागांझ यांचे अज्ञात गुणकk₁ व k₂ समी. (६) मध्ये वापरून नंतर समी. (५) व (६) ची बेरीजकेलीअसता

Σ (लॉग_e g _j /N _j  + k₁ + k₂ E _j ) δ N _j = 0 … … (७) समी. (७) ची उकल पुढीलप्रमाणे येते.

   

k₁ व k₂ ऐवजी पुढे दिलेली त्यांची मूल्ये वापरली असता

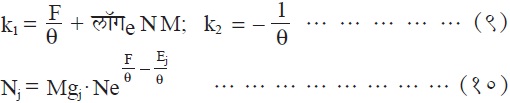
यात θ हा मापांक आहे. त्याचे मूल्य kT आहे (k बोल्टस्मान विश्वस्थिरांक व निरपेक्ष तापमान), हे पुढे दाखविले आहे सध्या ते गृहीत धरून व ΡN_j = N असल्याने, त्यात N_j चे समी. (१०) प्रमाणे मूल्य घालून Ne^F/θ चे मूल्य काढता येते ते वापरून असे दाखविता येईल की, 

 

Z हे अक्षर वापरून   

 N _j = Ng_j e^-Ej/KT/Z … … … … … … … … (११)

या प्रमाणे मॅ.- बो वितरण येईल.

 

  

ही महत्त्वाची राशी या राशीला वितरण अगर विभाजन फलन असे नाव आहे.

Z=e^-1/kT ………………………………….(१३) 

 हे समीकरण लिहिल्याने एकंदर समूहाची ऊर्जा व इतर ऊष्मागतिकीय राशी Z मध्ये लिहिता येतात.

उदा., समूह ऊर्जा E पुढीलप्रमाणे मांडता येईल. 

यावरून विभाजन फलन Z  चे महत्त्व लक्षात येते.

---

वरील समीकरणांपैकी काहींचे अनुप्रयोग पुढे दिले आहेत. दरम्यान स्टर्लिंग सूत्र न वापरता वैकल्पिक रीतीने N_j चे मूल्य मिळू शकते का ते पाहतात. स्टर्लिंग सूत्राचा वापरातील दोष पाहिलाच आहे. जर वैकल्पिक रीतीने मिळणारे N_j चे मूल्य स्टर्लिंग सूत्र वापरून काढलेल्या N_j च्या मूल्याशी (समी. ११) जुळत असेल, तर पुढेही सोयीचे म्हणून स्टर्लिंग सूत्र वापरण्यास प्रत्यवाय राहणार नाही. ही वैकल्पिक रीत जॉर्ज डार्विन व राल्फ हाऊऑर्थ फाऊलर यांची आहे. खरा उद्देश E_r ऊर्जा स्थितीत असलेल्या समूह घटकांची सरासरी संख्या N_r काढावयाची हा आहे. त्यासाठी प्रथम प्रत्येक N_r ला त्याच्या संभाव्यता w ने गुणतात व आलेल्या रकमेच्या बेरजेस w च्या बेरजेने भागतात. w  चे मूल्य समी. (१) प्रमाणे आहे व पाळावयाच्या शर्ती समी. (२) मध्ये दिल्याप्रमाणे आहेत. वर सांगितल्याप्रमाणे 

डार्विन – फाऊलर रीतीमधील बहुपदविस्तार, मिश्रचल, खडीउतरण पद्घती व पल्याणबिंदूचे धर्म या सर्वांचा उपयोग करून N_r चे मूल्य

  

असे येईल. वरील समीकरणात Z=e^-1/kT मांडल्यास 

  

असे मूल्य येईल. हे समी. (११) शी ताडून पाहता आणि j व r केवळ निर्देशक असल्याने r ऐवजी j वापरल्याने कोणताही फरक पडत नाही हे लक्षात घेता, दोन्ही समीकरणे एकच आहेत हे स्पष्ट दिसते. म्हणून स्टर्लिंग सूत्र वापरण्यात कोणताही धोका नाही ही गोष्ट स्पष्ट होते.

आता सांख्यिकीय दृष्ट्या तापमानाचा अर्थ निश्चित करण्याकरिता समी. (१) मधील राशींचा लॉग घेऊन व थोडे गणित करून असे दाखविता येईल की,

  

समूह  ऊर्जेमध्ये किंचितसा बदल झाला असे समजल्यास त्याचा परिणाम म्हणून थोडे बहिःकार्य d w घडेल व लॉग w  किंचित बदलेल. हा सर्व बदल

        θd लॉग_e w=dE+dw … … … … … … … … …  (१९) 

या समीकरणाने दर्शविता येईल. समी. (१९) ची उजवी बाजू लक्षात घेता हे समीकरण ⇨ ऊष्मागतिकीच्या पहिल्या नियमाचे सांख्यिकीस्वरूप आहे असे स्पष्ट दिसते. ऊष्मागतिकीचा पहिला नियम पदार्थासअल्प उष्णता दिल्यास त्यात होणारे बदल दाखवितो. तो नियम असा 

        dQ =dE + dw … … … … … … … … … (२०)

समी. (१९) व (20) यांची तुलना करता 

        θd लॉग w=dQ अथवा d लॉग w=dQ/θ … … (२१) 

लॉग w  या सांख्यिकीय राशीचा धर्म असा आहे की, त्याचे मूल्य विहित वितरणातील समूहाच्या स्थितीवरच फक्त अवलंबून आहे ती स्थिती कोणत्या मार्गाने प्राप्त झाली यावर ते मूल्य मुळीच अवलंबून नाही. यासाठी ही राशी एखाद्या ऊष्मागतिकीय स्थितिदर्शक चलाची सांख्यिकीय समधर्मी होऊ शकेल. हा ऊष्मागतिकीय चल म्हणजे एंट्रॉपी S व याची व्याख्या पुढीलप्रमाणे करतात.

         dS = dQ/T … … … … … … … … … … … (२२) 

यात dS हा एंट्रॉपी Sमधील अल्पसा बदल व T हे निरपेक्ष तापमान आहे. समी. (२१) व (२२) यांचा नीट विचार करता हा अर्थ स्पष्ट दिसतो की सांख्यिकीय वितरणातील  मापांक θ चे जागी kT  मांडणे युक्त होईल (यात k  हा बोल्टस्‌मान विश्वस्थिरांक आहे).

         म्हणजे θ=kT … … … … … … … … … … … … (२३) 

म्हणून समी. (२२) हे d लॉग w=^dQ/_kT

अथवा k  विश्वस्थिरांक असल्याने समी. (2४) प्रमाणे असे लिहिता येईल.

समी. (२४) चे समाकलन करून व त्यामुळे येणाऱ्या यास्थिरांकाचे जागी k  लॉग N!  लिहिले असता

  

हे समीकरण मिळते व यावरून एंट्रॉपीचा सांख्यिकीय अर्थ समजू शकतो. जर एखाद्या बंद समूहाच्या सुरूवातीच्या ऊष्मागतिकीय स्थितीत अव्युत्क्रमी बदल झाला तर एंट्रॉपी वाढेल. कारण बदल नेहमी अधिक स्थिर स्थितीकडे होत असल्याने बदलानंतरच्या स्थितीची संभाव्यता w  केव्हाही अधिक असते. नैसर्गिक वा आपणहून होणारा बदल नेहमी अव्युत्क्रमी असल्याने तो महत्तम एंट्रॉपीच्या दिशेने व महत्तम संभाव्यतेच्या दिशेने होईल. याप्रमाणे एंट्रॉपी व संभाव्यता समधर्मी राशी आहेत परंतु त्या सारख्या दिसल्या तरी त्यात एक मूलभूत फरक आहे. बंद प्रणालीची एंट्रॉपी अव्युत्क्रमी बदलामध्ये नेहमी वाढेल (ऊष्मागतिकीय नियम दोन प्रमाणे) परंतु सांख्यिकीय दृष्ट्या तशा तऱ्हेच्या बदलात एंट्रॉपी वाढण्याची संभाव्यता, फार मोठी आहे. त्याचबरोबर एंट्रॉपी कमी होण्याचीही संभाव्यता, ती कितीही अल्प असली तरी, नेहमी असते. इतरही ऊष्मागतिकीय स्थितिदर्शक फलनांची मूल्ये वितरण फलन Z च्या साहाय्याने मांडता येतात. हेल्महोल्ट्सची मुक्त ऊर्जा (A) समी. (२६)  प्रमाणे आणि दाब (P) समी. (२७) प्रमाणे दाखविता येतात.

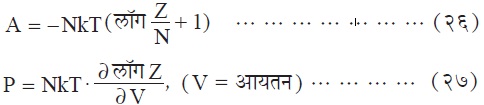
समूहातील एका कणाची सरासरी ऊर्जा E=E/N व समी. (१४) च्या  

  

मिळालेल्या काही समीकरणांचा अनुप्रयोग आदर्श वायूचे बाबतीत करता येईल. आदर्श वायू असंख्य रेणूंचा बनलेला असतो आणि रेणू मुक्त व अप्रभेद्य असतात. प्रत्येक रेणूचे वस्तुमान m,  वायूचा दाब P, निरपेक्ष तापमान T, आकाराचे आयतन (घनफळ) V  व रेणूंची संख्या N आहे असे समजू. p हा संवेग दर्शवितो व j गटातील रेणूचे संवेग अवयव  p_jx,  p_jy,  p_jz असे येतील. मागे सिद्घ केल्याप्रमाणे,

  

j गटाची आंगिक संभाव्यता त्याचे आयतनाचे प्रमाणात असल्याने असे समजू की, j गटातील रेणूचे कार्तीय सहनिर्देशक x_j व x_j+ Δx_j,  y_j व y_j+Δ_yj आणि Z_j व Z_j+Δ_Zj या अंतरात व संवेग सहनिर्देशक P_jX, व P_jX + Δ_jX, P_jy व P_jy,+ P_jy आणि P_jZ व P_jZ+ΔP_jZ यात सामावलेले आहेत. या सहा परिमाण असलेल्या अवकाशाला कोशिका रचना आहे व एकक कोशाचे आयतन h³(h = प्लांक विश्वस्थिरांक) आहे असे समजल्यास,  

  

पूर्णाक यावा म्हणून  

  

---

सहनिर्देशक स्वतंत्र असल्याने व घातीय राशीत x_j , y_j, z_j यांचा संबंध नसल्याने Δ x_j , Δ y_j , Δ z_j ची बेरीज स्वतंत्र रीत्या मांडता येईल म्हणजे

ΡΔ X_j. Δ y_j . Δ P_jZ = V… … … .. … … … … … … … (३२)  

म्हणून समी. (३१) मध्ये त्यात असलेले विशिष्ट गटाचे द्योतक j अक्षर टाकून वΡ चे ऐवजी समाकलन चिन्ह वापरून 

  

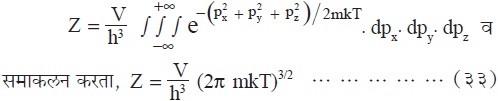
वरील Z चे मूल्य वापरून समीकरण (२६),(२७) व(२८)च्या साहाय्याने A, P व E मूल्ये आदर्श वायूंचे बाबतीत काढता येतील.

मॅक्सवेल यांचा वेगवितरणाचा सिद्घांत : याच पद्घतीने आदर्श वायूस लागू पडणारा मॅक्सवेल यांचा वेगांच्या वितरणाचा सिद्घांतही मिळू शकेल. तो असा: समीकरण (११) पुन्हा मांडले असता 

  

यात N_j चे ऐवजी dN मांडून, विशिष्ट गटाशी संबंध दर्शविणारे j अक्षर टाकून आणि समीकरणे (३०) व (३३) प्रमाणे g_j व Z यांची आणि समी. (२९) प्रमाणे E_j याचे मूल्ये मांडली असता,

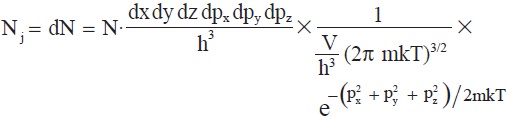
हे समीकरण मिळेल. आता dx dy dz हा आकार आयतनाचा अवयव कोठेही घेता येत असल्याने व घातीय राशीत त्याचा संबंध नसल्याने त्याची बेरीज करता येईल व तसे करता आकार आयतन V मिळेल. म्हणून 

 

u, v, w वेगाचे घटक मानल्यास, p_x =mu, dp_x =mdu इ.मूल्ये मिळतील. शिवाय

वरील मूल्ये समी. (३५) मध्ये प्रतिस्थापन करून शेवटी  

  

हे समीकरण मिळेल व यासच मॅक्सवेल यांचा वेगवितरणाचा सिद्घांत म्हणतात. 

ल्यूव्हील सिद्घांत व गिब्ज सांख्यिकी : वायूप्रमाणे घन व द्रव पदार्थांचा विचार करणे हेही भौतिकीय सांख्यिकीचे काम आहे. यासाठी त्या पदार्थास f मुक्तमात्रा असलेल्या (सर्वसाधारणपणे f &gt&gt 1 )गत्यात्मक प्रणाली समजाव्या लागतील. प्रणालीच्या स्थितीचा संपूर्ण निर्देश ‘ 2f ’ सहनिर्देशकांनी व त्यांच्या संयुग्मी संवेगांनी (म्हणजे q₁, q₂, …, q_f p₁, p₂, …, p_f यांनी) होतो. या स्थितीस अवस्था म्हणतात. वरील 2f राशींनी निश्चित केलेली अवस्था 2f  परिमित लंबकोणीय अवकाशात एका बिंदूने दर्शविली जाते. या अवकाशास प्रणालीचे अवस्था-अवकाश असे म्हणतात. p व q मध्ये कालांतराने बदल होत असल्याने अवस्था-बिंदू एक मार्ग आखतो. हा मार्ग स्वेच्छ नसून हॅमिल्टन यांच्या गतिसमीकरणानुरूप असतो. ही समीकरणे अशी : 

  

यात H हा हॅमिल्टोनिअन आहे.

समुदाय म्हणजे काय ते पुढे दिले आहे : हॅमिल्टोनिअन एकच असलेल्या पुष्कळ गत्यात्मक गटांचा समूह मानतात (उदा., प्रत्येकी एकच वस्तुमान व दृढता असलेल्या, परंतु ज्यांच्या अवस्था भिन्नभिन्न असून त्यांची शक्य मूल्ये पुष्कळ असतील असा सरल हरात्मक दोलकांचा समूह). अशा तऱ्हेच्या प्रणालीस गिब्ज यांनी समुदाय हे नाव दिले आहे.तसे पाहिले असता ही प्रणाली म्हणजे एकाच गत्यात्मक गटाच्या, भिन्नभिन्न अवस्था मूल्ये असलेल्या अनेक प्रतिकृती व या प्रतिकृतीच समुदायाचे घटक बनतात.

अवस्था-बिंदूच्या घनता D संबंधी एक महत्त्वाचा सिद्घांत आहे व त्यास ल्यूव्हील सिद्घांत म्हणतात. यास सांख्यिकीय भौतिकीतील सातत्याचे समीकरण असेही म्हणता येईल. अपसरण सिद्घांत 2f परिमित अवस्था-अवकाशास लागू पडेल असा व्यापक करून असे दाखविता येईल की,

दर्शविलेले अवकलन करता 

परंतु समीकरण (३७) चा उपयोग करता 

बदलामुळे होणारा D चा बदल दर्शविते. या गोष्टी लक्षात घेता समीकरण (३८) चे स्वरूप शेवटी खालीलप्रमाणे येते.

^dD/_dt=0 … … … … … … … … (३९)

समी. (३९) चा अर्थ असा की, अवस्था-घनता D चा कालाच्या दृष्टीने होणारा संपूर्ण त्वराक्रम शून्य असतो. अवस्था-बिंदू असलेल्या अवकाशाचा एखादा भाग कल्पिल्यास कालांतराने त्या भागातील बिंदूंचा ओघ असा वाहील, की त्या त्या आयतनाचा आकार जरी बदलला तरी त्यातील बिंदुसंख्या प्रत्येक क्षणी समान आयतनच व्यापील. गिब्ज यांच्या म्हणण्याप्रमाणे अवस्था-घनतेच्या अक्षय्यतेचे हे तत्त्व आहे.

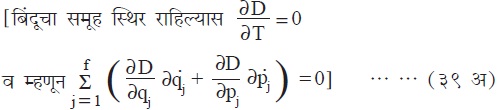
पृथ्वीच्या चुंबकीय क्षेत्रात होणाऱ्या इलेक्ट्रॉनाच्या गतीचा विचार करताना ल्यूव्हील सिद्घांताचा उपयोग केला आहे व विश्वकिरणांच्या अभ्यासात या गोष्टीला फार महत्त्व आहे. लघुविहित समुदायांचा विचार करताना गिब्ज यांनी हा सिद्घांत वापरला आहे. 

---

 

 

ऊर्जा ज्यात एका पट्टिकेत स्थिर न राहता सारखी बदलत राहते व ज्यातील अवस्था-अवकाशाच्या एकक आयतनातील घटनांची अंशतः संख्या ऊर्जेच्या बदलाप्रमाणे बदलत राहते, अशा जातीच्या प्रणालीस विहित समुदाय असे नाव आहे. यांचा उपयोग गिब्ज यांनी आपल्या सांख्यिकीत केला आहे. गिब्ज यांची विचारसरणी मागे म्हटल्याप्रमाणे दुसऱ्या जातीची आहे व ती पुंज सांख्यिकीस आधारभूत झाली आहे असे म्हणावयास हरकत नाही. गिब्ज यांच्या सांख्यिकीचा येथे विस्ताराने विचार केलेला नाही, परंतु त्याच्या साहाय्याने आदर्श वायूंच्या संबंधात मॅक्सवेल यांचा वेगवितरण सिद्घांत मिळू शकतो. तापमानाचा अर्थनिर्णय मॅक्सवेल –बोल्टस्‌मान सांख्यिकी प्रमाणेच होतो बंद घटक समूहाच्या एंट्रॉपीचे मूल्य मिळते व त्यावरून असे दिसते की एंट्रॉपीची वाढण्याकडे प्रवृत्ती असते व प्रत्यक्षात ती कधी कमी होत नाही. [⟶ एंट्रॉपी].

पुंज सांख्यिकी : यासाठी N अप्रभेद्य भौतिकीय घटकांची बनलेली एक प्रणाली विचारात घेतात. सर्व घटकांचे हॅमिल्टोनिअनचे रूप एकाच पद्घतीचे आहे. परंतु प्रत्येक हॅमिल्टोनिअन त्या त्या घटकाचे सहनिर्देशांकांचे (यात परिवलन सहनिर्देशकही आले) फलन आहे आणि प्रत्येक घटक स्वतंत्र व इतरांपासून वेगळा आहे. यापासून N श्रोडिंजर समीकरणे मिळतात ती अशी : 

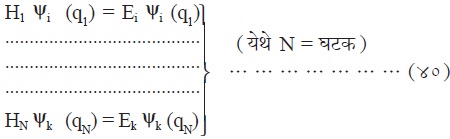
व सर्व समूह मिळून 

  

यात Ψ _i हे i गटाचे आयगेन फलन व E_i त्या गटाची ऊर्जा आहे.

ψ हे समूहाचे आयगेन फलन व E ही समूहाची एकंदर ऊर्जा आहे. E स्थिर राहून समूहातील दोन गटांची अदलाबदल केल्यास सर्वसाधारणपणे भिन्न फलन मिळेल, परंतु ऊर्जा तीच राहत असल्याने, ऊर्जेची द्विधा अपभ्रष्टता झाली असे म्हणता येईल स्थिर ऊर्जेची जितकी भिन्न आयगेन फलने, तितक्या पटीने ऊर्जेची अपभ्रष्टता होते.

पाउली यांचे विवर्जन तत्त्व आणि फेर्मी-डिरॅक व बोस-आइन्स्टाइन सांख्यिकी : गट जर इलेक्ट्रॉन वा प्रोटॉन यांचे असतील तर निसर्गतः मिळणारे संयोग सहनिर्देशांकांच्या अदलाबदलीस अनुलक्षून प्रतिसममित असतात म्हणजे प्रत्येक अदलाबदलामुळे मूल्य न बदलता फक्त चिन्ह बदलते व म्हणून आयगेन फलन ⇨ निर्धारक रूपात लिहिता येते. दोन निर्देशांकांची (उदा., q₁, q₂) अदलाबदल म्हणजे निर्धारकातील दोन स्तंभांची अदलाबदल व त्यामुळे फक्त चिन्हच बदलते. परंतु जर दोन घटक एकाच ऊर्जास्थितीत आले (म्हणजे i = j), तर निर्धारकाच्या दोन पंक्ती एकमेकांबरोबर होतील आणि निर्धारक व त्याबरोबर y देखील शून्य होतील. याचा अर्थ असा की समूहातील दोन विद्युत् कण घटक (दोन इलेक्ट्रॉन वा दोन प्रोटॉन) एकाच ऊर्जास्थितीत सापडणे शक्य नाही. यासच ⇨होल्फगांग पाउली यांचे विवर्जन तत्त्व असे म्हणतात. आता समजा दोन q च्या द्वंद्वात अदलाबदल झाली, तर चिन्ह बदलणार नाही व तेव्हा y सममित असते. हेही फलन निर्धारक रूपाने, परंतु त्यातील ऋण चिन्हांचे धन चिन्हात रूपांतर करून दाखविले जाते. याचे उदाहरण म्हणजे ड्यूटेरॉन अगर काही तटस्थ अणू. पुंज सांख्यिकीपैकी फेर्मी-डिरॅक सांख्यिकी प्रतिसममित जातीची व इलेक्ट्रॉन समूहास लागू पडणारी अशी आहे बोस-आइन्स्टाइन सांख्यिकी सममित जातीची असून ती फोटॉन वायूस लागू पडते. [⟶ पुंजयामिकी].

पाउली यांच्या विवर्जन तत्त्वाप्रमाणे निसर्गात प्रत्यक्ष आढळणाऱ्या प्रणालीतील गटसंख्या दाखविणारे N₀, N₁, N₂, N₃, … N_r , … यांचे प्रत्येकी मूल्य एकापेक्षा अधिक असूच शकणार नाही यावरून q संभाव्यतेचे मूल्यही लगेच ठरते म्हणजे कोणत्याही परिसीमित समूहाच्या बाबतीत,

          जर N_r (कोणताही N_r )=0 असेल, तर संभाव्यता =१ …(४३) N_r च्या कोणत्याही इतर मूल्यास संभाव्यता शून्य होते म्हणजे

           जर N_r≠ 0, १ तर संभाव्यता = 0 … … … (४३ अ)

या शर्तीखाली जर सरासरी गटांची संख्या N_r समी. (१५)च्या साहाय्याने काढली तर ती फेर्मी-डिरॅक सांख्यिकीप्रमाणे होईल. परंतु ज्याचे आयगेन फलन सममित आहे अशा प्रणालीचा विचार करण्यात आला, तर N₀, N₁, … इत्यादींचे कोणतेही मूल्य असले तरी चालत असल्याने शर्त पुढीलप्रमाणे होईल : 

           N_r =कोणतेही मूल्य, संभाव्यता = १            … … … (४४) 

या शर्तीखाली येणारी ती बोस-आइन्स्टाइन सांख्यिकी होईल. या दोन सांख्यिकी दरम्यान मॅक्सवेल-बोल्टस्‌मान यांची रूढ सांख्यिकी येते. याचा अर्थ आता असा : हिच्यात गट अगर कोश यांची संख्या कण अगर वस्तूच्या मानाने इतकी मोठी आहे की प्रत्यक्षात कोणत्याही एका स्थितीत (कोशात) एकापेक्षा अधिक कण सापडणे अशक्यप्रायच असते. 

आता E_j व E_j + dE_j या छोट्या ऊर्जापट्टिकेत व म्हणून सर्वसाधारणतः प्रत्येकी E_j ऊर्जा असलेल्या समसमान N_j कणांची n_j कोशात (अ) बोस-आइन्स्टाइन (बो.-आ.) सांख्यिकीप्रमाणे आणि (आ) फेर्मी-डिरॅक (फे.-डि.) पद्घतीने स्टर्लिंग सूत्र वापरून विभागणी पुढे दिली आहे. डार्विन-फाऊलर रीती वापरून तीच मूल्ये मिळतात.

(अ) बो.-आ. प्रणाली : एका कोशात कणांची संख्या कितीही असू शकेल हे ध्यानात ठेवून N_j कणांची n_j कोशात होऊ शकणारी

वितरण संख्या  (n_j + N_j – 1)!  इतकी येते व म्हणून शक्य स्थितींची संख्या w पुढीलप्रमाणे येईल.

                          (n _j − 1)! N _j ! 

(आ) फे.-डि. प्रणाली : कोणत्याही एका कोशात एकापेक्षा अधिक कण असूच शकणार नाहीत ही शर्त लक्षात घेता N_j ≤n_j आणि वितरण संख्या     इतकी येते व म्हणून

याशिवाय मॅ.-बो. सांख्यिकीप्रमाणेच वरील दोन सांख्यिकीतही पुढील दोन शर्ती पाळावयास लागतातः 

   ΣN_j=N (स्थिरांक)

   ΣN_jE_j=E (स्थिरांक) 

 

समीकरणे (४५) व (४६) यांचा लॉग घेता, स्टर्लिंग सूत्र वापरता व n_j चे तुलनेने १ ही संख्या उपेक्षणीय म्हणून सोडून दिली असता,

याप्रमाणे अनुक्रमे बो.-आ. व फे.-डि. सांख्यिकींसंबंधी समीकरणे मिळतात. यानंतर लाग्रांझ यांचे अज्ञात गुणक k₁, k₂ वापरले व वितरण संभाव्यता महत्तम समजली असता,

 

(अ) बो.-आ.सांख्यिकी समी. (४७) प्रमाणे लॉग w याचे मूल्य वापरता समी. (४९) पासून लॉग (n_j+N_j) – लॉग N_j–k₁ – k₂ E_j =0 हे समीकरण मिळते अथवा रूपांतर केले असता,

 

(आ) फे.-डि.सांख्यिकी समी.(४८) प्रमाणे लॉग w याचे मूल्य समी. (४९) मध्ये वापरले असता,

लॉग (n_j−N_j) −लॉग N_j−k₁ −k₂E_j =0 अथवा रूपांतर केले असता,

 

हे समीकरण मिळते. वरील समीकरणे (५०)व (५१) एकत्र लिहिता येतील ती अशी : 

 

यात छेदातील ऋण चिन्ह बो.-आ. सांख्यिकीस अनुलक्षून व धन चिन्ह फे.-डि. सांख्यिकीस अनुलक्षून आहे. समीकरणे (५०) व (५१) यांमध्ये अनुक्रमे बो.-आ.व फे.-डि.सांख्यिकींचे वितरण फलन मिळते.समीकरणे (५०), (५१) वा (५२) मध्ये छेदात असलेली e^k1 ही राशी फार मोठी समजल्यास, तिचे तुलनेने १ ही संख्या उपेक्षिता येईल व नंतर येणारे समीकरण मॅ.-बो.सांख्यिकींचे वितरण फलन दाखवील म्हणजे

     Nj =n_j ×e^{– k}1 ^–k2^Ej … … … … … … … … (५३)

समी. (५३) ची तुलना समी. (११) शी करता मांडल्यास दोन्ही समीकरणे एकच आहेत हे दिसून येईल.या सर्व समीकरणांत [(५०), (५१),(५२) व (५३)] k₂ =1/ kT.

पुंज प्रणाली (बो.-आ.आणि फे.-डि.सांख्यिकी) n _j चे मूल्य बाजूंची लांबी l₁ l₂ l₃  असलेल्या एका बंद समांतर फलक आयताकृतीमध्ये संचार करणाऱ्या मुक्त कणांच्या गतीचा विचार केला असता त्याच्या ऊर्जेची आयगेन मूल्ये पुढीलप्रमाणे मिळतात. 

यात n₁, n₂, n₃ पूर्णांक आहेत व प्रत्येक (n₁, n₂, n₃) च्या गटाशी शक्य असलेल्या ऊर्जेचे मूल्य निगडित आहे h प्लांक विश्वस्थिरांक आहे व m हे कणाचे वस्तुमान आहे. ऊर्जामूल्यांस अनुरूप असे आयगेन फलन पुढीलप्रमाणे आहे.

 

ऊर्जेच्या E_j व E_j + dE_j या छोट्या अंतरातील ऊर्जामूल्याची [ E (n₁, n₂, n₃)] संख्या खालीलप्रमाणे येते हे सिद्घ करता येईल व तीच कोशांची संख्याही दर्शविते. म्हणून

 

 

यात V हे आकार आयतन असून हे n_j याचे मूल्य समी. (५२) मध्ये वापरून,

 

हे समीकरण मिळते. परिवलन शून्य कणांस समी. (५७) आहे त्या स्वरूपात वापरता येईल. इलेक्ट्रॉनाच्या बाबतीत त्याच्या उजव्या बाजूस दोनने व कणांचा अणुकेंद्रीय परिवलन पुंजांक S असल्यास (2S + 1) ने गुणावे लागेल.

फे.-डि.सांख्यिकीने अतिअपभ्रष्टता वायूचा (उदा.,इलेक्ट्रॉन वायू) विचार करून परमशून्य तापमानात शिल्लक असलेल्या ऊर्जेचे मूल्य काढता येते.⇨रॉबर्ट बॉइल व ⇨झाक आलेक्सांद्र सेझार चार्ल्स यांच्या सूत्राबरहुकूम वागणाऱ्या वायूस आदर्श वायू म्हणतात. अशावायूंच्या स्थितीपासून एखादा वायू विचलित होऊ शकेल व हाविचलितपणा थोडा वा फार असू शकेल. आदर्श वायूच्या स्थितीपासूनथोड्या प्रमाणात विचलित झालेल्या वायूस किंचित अपकर्षित वायू वफार प्रमाणात विचलित झालेल्या वायूस अतिअपकर्षित वायू म्हणतात.अशा दोन्ही तऱ्हेच्या वायूंना लागू पडणारी बो.-आ. आणि फे.-डि.सूत्रे काढता येतात परंतु किंचित अपकर्षित वायूंच्या संबंधात त्यासूत्रांवरून निघणाऱ्या निष्कर्षास विशेष अर्थ नसल्याने त्यांचा येथे विचारकेला नाही व फक्त अतिअपकर्षित वायूंविषयींच्या सूत्रांचाच विचार केलाआहे.येथे उल्लेखिलेल्या अपकर्षणाचा पुंजयामिकीत आढळणाऱ्या अपकर्षणाशी काहीही संबंध नाही.

रूढ सांख्यिकीप्रमाणे तापमान (T) शून्य झाल्यास ऊर्जाही शून्य होते. E₀ परमशून्य ऊर्जा असेल तर सिद्घ करता येईल की,

  

एंट्रॉपीचे सर्वसाधारण मूल्य वरील वायूंच्या बाबतीत पुढीलप्रमाणे येते. 

 

 

तर वरील समीकरणावरून स्पष्ट दिसते की S ⟶0. तसेच रूप्यासारख्या घन पदार्थाची विशिष्ट उष्णता (C) यामधील इलेक्ट्रॉनाचे अंशदान फे.-डि.सांख्यिकीने काढल्यास ते बरोबर येते. रूढ पद्घतीने हे अंशदान 3 R/2, (R =वायूस्थिरांक) येते परंतु हे मूल्य फार जास्त आहे. म्हणून सर्वसाधारण तापमानात रूप्यासारख्या घनपदार्थाच्या विशिष्ट उष्णतेचे मूल्य प्रायोगिक मूल्याशी मुळीच जुळत नाही. फे.-डि. सांख्यिकीप्रमाणे रूप्याचे बाबतीत ३०० के.(केल्व्हिन निरपेक्ष तापमान) असताना हे अंशदान 2·4 ×10^-2 R इतके येते. हे मूल्य अल्प आहे व म्हणून सैद्घांतिक व प्रायोगिक मूल्ये एकमेकांशी जुळतात.

---

याखेरीज या फे.-डि.सांख्यिकीचे उपयोजन (१) धातूचे विद्युत् व  औष्णिक गुणधर्माचे विवेचन करण्याकडे आणि झेबेक, पेल्‌त्ये व टॉमसन गुणांकांची मूल्ये काढण्याकडे, (२) स्फटिक जालकातून होणारी इलेक्ट्रॉनांची हालचाल, (३) इलेक्ट्रॉनांचे तापायनिक उत्सर्जन, (४) वर्चस् अवरोधकातून होणारे इलेक्ट्रॉनांचे संचारण, (५) प्रकाशविद्युत् परिणाम इ.गोष्टींचा अभ्यास करण्याकडे झाला आहे.

फोटॉन वायूसारख्या अतिअपकर्षित वायूचे बाबतीत बो.-आ. सांख्यिकी उपयोगात येते व त्यावरून प्लांक यांचा प्रारण सिद्घांत मिळू शकतो. तो असा,

N_j याचे बो.-आ.समीकरण पुन्हा लिहिले असता,

फोटॉनाचे स्थिर वस्तुमान शून्य असल्याने त्याचे बाबतीत k₁ = 0 आणि E =hn_j, pj =hn_j / c (c =प्रकाशवेग) याप्रमाणे मूल्ये वरील समीकरणात लिहिली व जरूर तो फरक केला असता खालील समीकरण मिळते.

फोटॉनाच्या परिवलनामुळे समी. (५९ अ) च्या उजव्या बाजूस २ ने गुणून व N_j ऐवजी dN लिहून तसेच विशिष्ट दर्शकांक j गाळूनn व n+ dn या लहान कंप्रता पट्टिकेत असलेल्या फोटॉनाची एकक आयतनामधील संख्या खालील सूत्राप्रमाणे मिळेल. 

या पट्टिकेत प्रत्येक फोटॉनाची ऊर्जा hnअसल्याने, ऊर्जेची सरासरी घनता खालीलप्रमाणे असेल,

समी. (६०) म्हणजेच प्लांक यांचा प्रारण सिद्घांत आहे.  

बो.-आ. सांख्यिकीच्या साहाय्याने अतिअपकर्षित वायूच्या संबंधात, विशिष्ट तापमानात, कणांची एकक आयतनामधील संख्या (घनता)

इतकी येते असे दाखविता येईल यातील महत्त्वाची गोष्ट म्हणजे दिलेल्या तापमानात ही समतोल घनता महत्तम असते. त्याचप्रमाणे

व दाब   असल्यामुळे

इतका येतो. या समीकरणावरून स्पष्ट दिसते की, बो.-आ. अतिअपभ्रष्टता वायूचा दाब फक्त तापमानावरच अवलंबून आहे (संपृक्त बाष्पाप्रमाणे) म्हणून अनुमान काढता येते की, जर तापमान पुरेसे खाली नेले तर एका तऱ्हेची गोठणक्रिया घडून त्यामुळे अधिक ऊर्जा असलेल्या स्थितीतून काही कण निघून ते लघुतम ऊर्जेच्या स्थितीत जातात व ह्या स्थितीत त्यांचा दाब निर्माण करण्याच्या दृष्टीने काहीही उपयोग होत नाही. या गोठणक्रियेस संवेग अवस्थेतील गोठण असे नाव दिले गेले आहे. याचा उपयोग संक्रमण बिंदूच्या आसपास (l-बिंदू, २·१९ के.) द्रव हीलियमाच्या गुणधर्माचे विवरण करताना फ्रिट्स व्होल्फगांग लंडन यांनी केला आहे. 

आदर्श द्विअणू वायू : नायट्रोजन, ऑक्सिजन यांसारख्या वायूंचा यात समावेश होतो. अशा वायूंच्या बाबतीत रेणूची ऊर्जा सरल गती, वलन गती व दोलन यांच्यामुळे उत्पन्न होत असल्याने जर ह्या ऊर्जा अनुक्रमे E_t, E_r व E₀ अशा दर्शविल्या, तर सामान्य तापमानात रेणूची समग्र ऊर्जा E या ऊर्जांच्या बेरजेइतकी असते.

E =  E_t + E_r + E₀ … … … … … (६४)

वितरण फलन खालीलप्रमाणे असते,

Z =Z_t . Z_r . Z₀ … … … … … (६५)

यात Z_t हे सरल गतीचे वितरण फलन आहे व याचा विचार मागे केलेलाच आहे. आता

 

यात h हा प्लांक स्थिरांक असून I रेणूची निरूढी आहे. (h²/8π²I.kT ) =sलिहीता व हायड्रोजनाचा अपवाद वगळता बहुतेक सर्व द्विअणुरेणूंचे बाबतीत सामान्य तापमानात s&lt &lt 1 व उकळबिंदूच्या जवळपास s&lt1.

sएकापेक्षा कमी असल्यास,

  

आणि रेणूच्या वलन गतीमुळे त्याच्या विशिष्ट उष्णतेत झालेली वाढ 

  

उच्च तपमानात s⟶0 व म्हणून Cr =^k/_m. त्याचप्रमाणे द्विअणुरेणूच्या दोलन गतीचा विचार करता दोलन गतीचे वितरण फलन

यामुळे रेणूच्या विशिष्ट उष्णतेत झालेली वाढ 

हायड्रोजनाच्या बाबतीत तापमान ३०० के. (सामान्य तापमान) असताना  म्हणजे जवळजवळ नाहीच व म्हणून सामान्य तापमानात दोलन गतीमुळे विशिष्ट उष्णतेत लक्षात घेण्यासारखी भर पडत नाही. म्हणून सामान्य तापमानात रेणूची एकंदर विशिष्ट उष्णता (C)

 

तापमान वाढेल तसतसे C₀ वाढत जाते.

---

लोरेन्ट्स-झोरफेल्ड विद्युत् व ऊष्मीय संवहन सिद्घांत : रूपे,तांबे यांसारख्या धातूंच्या विद्युत् व ऊष्मीय संवहनासंबंधी हेंड्रिक आंटोन लोरेन्ट्स व आर्नोल्ट झोरफेल्ड यांनी विवेचन केले असून तत्संबंधी आपला सिद्घांत मांडला आहे. दोन्ही संवहने लोरेन्ट्स यांच्या मते धातूमधील मुक्त इलेक्ट्रॉनांमुळे (दर अणूस एक) घडतात. या मुक्त इलेक्ट्रॉनांच्या समूहास इलेक्ट्रॉन वायू म्हणू या वायूचा विचार लोरेन्ट्स यांनी मॅ.-बो.सांख्यिकीय पद्घतीने केला त्यानंतर झोरफेल्ड यांनी तो वायू अतिअपकर्षित आहे असे मानून त्याचा विचार फे.-डि.सांख्यिकीने केला, त्याचे थोडक्यात दिग्दर्शन पुढे केले आहे धातूची एक बारीक कांब क्ष-अक्षास समांतर ठेवली असून  क्ष– अक्षास दिशेनेच तिला विद्युत् क्षेत्र E लावलेले आहे असे समजू. इलेक्ट्रॉनांच्या अणूंशी होणाऱ्या टकरीमुळे विद्युत् क्षेत्रात होणारा फरक X त्यांनी काढला, तो असा

यात l हा सरासरी मुक्त मार्ग असून, m,  e, v इलेक्ट्रॉनाचे अनुक्रमे वस्तुमान, विद्युत् भार व वेग आहेत. f₀ हे स्थितिनिर्देशांक (x, y, z) व वेगघटक (v_x, v_y, v_z) यांचे फलन आहे.यानंतर विद्युत् प्रवाह घनता (J) व ऊष्मीय प्रवाह घनता (C) यांची समीकरणे मांडली, ती अशी :

यात f =f₀ + v_x  X. आवश्यक ते गणित कृत्य करून

 

विद्युत् संवहन गुनांक

त्याचप्रमाणे

व ऊष्मिय संवहक गुणांक

या समीकरणात A₁, A₂, A₃ ची मूल्ये घालून व आसन्नता वापरली असता

  अर्ग / (^० से.)^२ (ई.एम. यू.)^२ . . . . .(७४) 

२९३ के.तापमानात तुलनेसाठी खाली प्रायोगिक मूल्यांचे कोष्टक दिले आहे. त्यावरून दिसून येईल की,

याची सैद्घांतिक व प्रायोगिक मूल्ये जुळणारी अशी आहेत : 

_______________________________________________________

तापमान/धातू        तांबे         रुपे          सोने        जस्त       कॅडमियम               शिसे        लोह

_______________________________________________________

२९१ के.                  २·२८      २·३६      २·४३      २·३१      २·४२                      २·४५      २·८८

३७३ के.                  २·३२      २·३७      २·४५      २·३३      २·४३                      २·५१      ३·००

_______________________________________________________

रूढ सिद्घांताप्रमाणे चे मूल्य  येत होते व ते प्रायोगिक मूल्याशी जुळत नव्हते.याच तत्त्वांवर ऊष्माविद्युतमधील झेबेक, पेलत्ये व टॉमसन प्रभावाचा खुलासा व गुणांकांची सैद्घांतिक मूल्ये मिळू शकतात.

पहा : ऊष्मागतिकी एंट्रॉपी द्रव्याचा गत्यात्मक सिद्घांत पुंजयामिकी बाउनीय गति.

संदर्भ :1. Betts, D. S. Introduction to Statistical Mechanics, 1992.

            2. Garrod, C.Statistical Mechanics and Thermodynamics, 1995.

            3. Greiner, W. Neise, L. Stocker, H. Thermodynamics and Statistical Mechanics, १995.

            4. Huang, K. Statistical Mechanics, 1987.

            5. Kubo, R. and others, Statistical Physics, 2 vols ., 1991.

            6. Landau, L. D. Lifshitz, E.Statistical Physics, 1980.

           7. Tolman, R. C. The Principles of Statistical Mechanics, 1938, (reprint 1980).

           8. Trevens, D. H. Statistical Mechanic: An Introduction, 1993.

भावे, श्री. द.

“