एकके व परिमाणे

एकके व परिमाणे : सर्व व्यावहारिक व प्रायोगिक शास्त्रांत मोडणार्‍या राशींच्या मापनाला अत्यंत महत्त्व आहे. किंबहुना निरीक्षण व मापन म्हणजेच शास्त्र असेही म्हणण्यास हरकत नाही. भौतिकीत मापनाच्या पद्धतींचा सैद्धांतिक व व्यावहारिक दृष्ट्या सांगोपांग विचार केलेला असून, त्या पद्धतींचे अनुकरण अनेक शास्त्रांत झालेले आहे.

या शास्त्रातील विविध राशींचे मापन करताना जी एकके वापरतात किंवा वापरावयाची आहेत त्या एककांच्या राशी तरी कोणत्या म्हणून निवडावयाच्या व त्याच का निवडावयाच्या व त्या कशा निवडावयाच्या, हे प्रश्न प्रथम सोडवावे लागतात. शास्त्रात मोडणाऱ्या हजारो राशींसाठी संपूर्णपणे स्वतंत्र अशी हजारो एकके निर्माण करणे हे अगदी गैरसोयीचे तर आहेच पण ते अशास्त्रीयही आहे, म्हणून इष्ट नाही. पुन्हा सर्वच राशी अगदी मूलभूत व परस्परांशी असंबंधित असतात असेही नव्हे.

मूलभूत राशी व त्यांवर आधारलेल्या एकक पद्धती : कोणत्याही राशीच्या मापनास अवकाश, वस्तुमान व काल या तीन प्रमुख व मूलभूत राशी गृहीत धरणेच सोईस्कर व इष्ट आहे, असा अनेक शतकांच्या अनुभवातून व प्रगतीतून निघालेला निष्कर्ष आहे. विशिष्ट शाखेतील राशींच्या मापनास वरील तीन मूलभूत राशींशिवाय आणखी तीन सोईस्कर राशी मूलभूत म्हणून स्वीकारणे जरूर पडते हा अलीकडील निष्कप्ष आहे. अवकाश, वस्तुमान व काल या मूलभूत राशींवर आधारित अशा एकक पद्धतीस केवल किंवा स्वेच्छ एकक पद्धती असे म्हणतात. वस्तुमान या राशीचा उगम, नेहमी अनुभवास येणाऱ्या प्रेरणा या राशीतून होत असल्यामुळे मापनाच्या एका पद्धतीत अवकाश, प्रेरणा व काल या मूलभूत राशी म्हणून गणल्या गेल्या आहेत. या मापनाच्या पद्धतीस गुरुत्वीय एकक पद्धती असे नाव आहे.

अवकाश (स्थल) व काल या राशींचा अनुभव प्रत्येकास पदोपदी येतो. कोण, कोठे, केव्हा, कसे किती व काय या प्रश्नावलीमधील कोठे व केव्हा हे अनुक्रमे अवकाशसूचक व कालसूचक शब्द आहेत. व्यानहारिक शास्त्रातील सर्वच राशी या मूळ राशींनी वा मूलतत्त्वांनी बांधल्या आहेत व त्यावर आधारलेल्या आहेत. वस्तुमान किंवा द्रव्यमान ही एक निश्चित व मापनक्षम राशी आहे असे माणने भागत पडते. विद्युत् चुंबकीय राशी, ऊष्मीय राशी व प्रकाशविषयक राशी यांच्या मापनासाठी आणि परिमाणासाठी त्या त्या शाखेतील आणखी प्रत्येकी एक एक राशी मूलभूत म्हणून धरावी लागते.

मूलभूत राशी, एकके, मापन पद्धतीतील अचूकता व सापेक्ष मापन मूल्यांची स्वतंत्रता : अवकाश, वस्तुमान (अथवा प्रेरणा) व काल या तीन मूलभूत राशी म्हणून गणल्यानंतर दोन प्रमुख एकक पद्धती तयार करता येतात, असा वर उल्लेख आला आहे. तरी पण या मूलभूत राशींची एकके काय मूल्याची घ्यावीत व त्यांची काय नावे असावीत, हे प्रश्न पूर्वी शास्त्रीय पद्धतीनेच सोडवले गेले होते असे मात्र नाही. वेगवेगळ्या देशांत पूर्वापार चालत आलेल्या रीतिरिवाजानुसार भिन्नभिन्न नावे व मूल्ये प्रचारात होती. त्यांच्यातील परस्पर संबंधात विशेष प्रकारची संगती व सुसूत्रता नव्हती. भारतवर्षात काय किंवा इतर देशांत काय, ज्या भव्य सौंदर्यपूर्ण कायम स्वरूपाच्या अप्रतिम शिल्पाकृती तयार झाल्या, त्या कोणत्यातरी मापनपद्धतीस धरूनच असल्या पाहिजेत, हे उघड आहे. पण त्या त्या देशात त्या त्या मापनाच्या पद्धतीला मान्यता असली तरी त्या पद्धती सर्वत्र एकमुखी (बव्हंशी राजकीय कारणांमुळेच) मान्यता पावल्या नव्हत्या. त्यामुळे सध्या जशा शास्त्रीय व व्यावहारिक क्षेत्रातसुद्धा काही मापन पद्धती सर्रास मान्यता पावल्या आहेत व वापरात आहेत तशा पूर्वी नव्हत्या. विविध राशींच्या मापन पद्धतींचा इतिहास ‘कालमानप’, ‘मेट्रिक पद्धती’, ‘लांबी, क्षेत्रफळ व घनफळ यांची एकके’, ‘वजने व मापे’ इ. स्वतंत्र नोंदींत दिलेला आहे.

ब्रिटिश पद्धतीमध्ये लांबीच्या (अवकाश या अर्थी) मापनाचे एकक फूट आहे, वस्तुमानाचे पौंड आहे व कालाचे सेकंद आहे (एफ. पी. एस. पद्धती), लांबी व वस्तुमान यांच्या एककाच्या निवडीला काहीही नैसर्गिक अथवा सैद्धांतिक अशी बैठक नाही. स्वेच्छेनेच त्यांची निवड झाली आहे. कालाच्या एककाची निवड सूर्याच्या भासमान गतीवरून झाली असल्यामुळे त्या एककाला काही नैसर्गिक बैठक आहे असे म्हणता येईल.

शास्त्रीय जगात सर्वमान्य झालेली फ्रेंचांची मेट्रिक मापन पद्धती आहेत. त्यात लांबीच्या एककाला सेंटिमीटर, वस्तुमान एककाला ग्रॅम व काल एककाला सेकंद अशी नावे आहेत (सी. जी. एस. पद्धती). प्रारंभी लांबीच्या एककाची निवड करताना ते एका नैसर्गिक राशीवर आधारण्याचा प्रयत्न केला होता. परंतु ह्यात काही चूक आहे असे आढळून आले. १ मीटर = निर्वातावस्थेतील अक्षोभित क्रिप्टॉन (८६) च्या अणूच्या 2P₁₀ ते 5d₅ या ऊर्जापातळींमधील संक्रमणामुळे होणाऱ्या उत्सर्जित प्रकाशाच्या तरंगलांबीच्या १६,५०,७६३·७३ पट १ सेंमी. = ^१/^_१०० मीटर. तसेच १ ग्रॅम = प्लॅटिनम-इरिडियमाच्या केलेल्या आद्यरूप १ किलोग्रॅमचा ^१/_१००० भाग आणि १ सेकंद = सिझियम (१३३) अणूच्या (F = ४, M = ०) ते (F = ३, M = ०) या संक्रमणातून उत्सर्जित होणाऱ्या प्रकाशाच्या ९,११,२६,३१,७७० आवर्तनांस लागणारा कालखंड या व्याख्याही त्यानंतर मान्य करण्यात आल्या.

सध्या वरील एककांच्या ऐवजी मीटर, किलोग्रॅम, सेकंद ही एकके असलेली त्यांच्या नावांच्या आद्याक्षरांनी प्रसिद्ध असलेली एम. के. एस. (मीटर, किलोग्रॅम, सेकंद) ही पद्धती अधिकाधिक प्रचारात येत आहे. विद्युत् चुंबकीय शाखेतही या मापन पद्धतीचा उपयोग केला जातो.

गुरुत्वीय मापन पद्धतीनुसार ब्रिटिशांची लांबी, प्रेरणा व काल यांच्या एककांची नावे अनुक्रमे फूट, पौंड, वजन व सेकंद अशी आहेत. फ्रेंचांची या पद्धतीतील एककांची नावे सेंटिमीटर, ग्रॅम वजन व सेकंद अशी आहेत. अभियांत्रिकीत या पद्धतीचा जास्त उपयोग करतात.

मापनाची अचूकता एककाच्या निवडीवर अवलंबून नसते. ती अचूकता मापनासाठी वापरलेल्या पद्धती व उपकरणे यांवर अवलंबून असते. एखाद्या राशीचे संख्यात्मक वर्णन म्हणजे तिचे मूल्य होय. उदा., दोन वस्तूंचे घनफळ एकाच एकक पद्धतीत दिले आहे असे समजू तर त्या दोन घनफळांचा जो भागाकार येईल किंवा त्यांचे परस्परांशी जे गुणोत्तर येईल ते प्रमाण एकक पद्धती बदलल्या अथवा त्यातील एककांचे मूल्य निरनिराळे घेतले तरीही बदलणार नाही. याचा अर्थ असा की, दोन भिन्न वस्तूंच्या घनफळांच्या एकाच एकक पद्धतीनुसार केलेल्या संख्यात्मक वर्णनाचे गुणोत्तर अबाधित व निश्चित असते. याचे काय कारण आहे याचा थोडा विचार पुढे केला आहे.

साधित एकके व त्यांची परिमाणे : मूलभूत राशींची व त्यांच्या एककांची एकदा निवड झाल्यावर व्याख्यारूपाने अनेक राशींचा संबंध मूलभूत राशींशी जोडता येतो व या संबंधावरून अनेक राशींची एकके तयार होतात, त्यांना साधित एकके म्हणतात. अगदी सामान्य व नेहमीच्या वापरात असलेल्या राशी उदा., क्षेत्रफळ व घनफ घेऊ. व्याख्येने क्षेत्रफळ हे लांबी व रुंदी (एकमेकांस काटकोन करीत आहेत असे गृहीत धरून) यांचा गुणाकार करून मिळते. म्हणून मूलभूत राशींपैकी लांबी या राशीला त्याच प्रकारच्या राशीने म्हणजे रुंदीने गुणावयाचे असल्यामुळे क्षेत्रफळ या साधित राशीचा संबंध लांबी या मूलभूत राशीच्या वर्गाशी जोडला गेला. हेच वर्णन आता गणिती भाषेत करावयाचे झाल्यास लां या लांबीच्या आद्याक्षराने मूलभूत राशी दर्शविली तर क्षेत्रफळाची तयार होणारी साधित राशी लां^२ अशी होईल. जर लां यांचे एकक फूटात धरले असेल, तर लां^२ किंवा क्षेत्रफळ राशीचे साधित एकक ‘चौरस फूट’ होईल. त्याचप्रमाणे व्याख्येनुसार घनफळ म्हणजे लांबी × रुंदी × उंची = लां^३ होत असल्यामुळे घनफळाचे साधिक एकक ‘घन फूट’ असे होईल. लां चे एकक सेंटिमीटर अथवा मीटर धरले तर वरील राशींची साधित एकके अनुक्रमे चौरस सेंटिमीटर, चौरस मीटर, घन सेंटिमीटर व घन मीटर अशी होतील. या विवरणावरून स्पष्ट होईल की, क्षेत्रफळ किंवा घनफळ या राशी मूलभूत राशींपैकी केवळ अवकाशदर्शक लां ह्या राशीवरत अवलंबून आहेत. बाकीच्या मूलभूत राशी म्हणजे वस्तुमानदर्शक व आणि कालदर्शक का यांच्याशी त्यांचा कसलाही संबंध नाही. म्हणून क्षेत्रफळ व घनफळ या राशी वस्तुमान आणि काल यांच्यावर बिलकूल अवलंबून नाहीत. गणिताच्या परिभाषेत ही गोष्ट पुढील प्रमाणे व्यक्त केली जाते :

[ क्षेत्रफळ ] = लां ^२ व^० का^०

[घनफळ ] = लां ^३ व^० का^०

या वर्णनात मूलभूत राशीदर्शक आद्याक्षराचे जे घातांक आहेत त्या अंकांना त्या त्या राशीची परिमाणे म्हणतात. क्षेत्रफळाची परिमाणे लांबीत २, वस्तुमानात ० कालात ० आहेत.

न्यूटन यांच्या गतिविषयक दुसर्‍या सिद्धांतानुसार प्रेरणेची व्याख्या वस्तुमान गुणिले प्रवेग (वेग बदलाचे प्रमाण) अशी होते. म्हणजे प्रेरणेचे एकक = वस्तुमानाचे एकक × प्रवेगाचे एकक

[ प्रेरणा ] = व^१ × लां^१ का^-२ अशा तर्‍हेने किंवा वस्तुमानात + १, लांबीत + १ व कालात – २ अशा तर्‍हेने प्रेरणेची परिमाणे दाखवितात. थोडक्यात व्याख्येनुसार राशीच्या एककाचे वर्णन मूलभूत एककात करताना त्यांचे जे घातांक येतात त्या घातांकांना त्या राशींची परिमाणे म्हणतात.

परिमाणे, त्यांचे कार्य व उपयोग : भौतिकीत ज्या बहुविध व अनेक राशींचा अभ्यास केला जातो त्यांचा मूलभूत राशींशी व्याख्यारूपाने काहीतरी संबंध प्रस्थापित केलेला असतो. या संबंधावरून त्या त्या राशीचे एककही तयार करता येते. मूलभूत राशींच्या घातांकासहित केवळ गुणाकार व भागाकार यांनी इतर कोणत्याही राशीचे गणित वर्णन करता येत असल्यामुळे कोणत्याही एकाच एकक पद्धतीनुसार व्यक्त केलेल्या विशिष्ट भौतिकीय राशींच्या मूल्यांचे गुणोत्तर हे निरपेक्ष व अबाधित असते. थोडक्यात कोणत्याही राशीची परिमाण-सूत्रे ही मूलभूत राशींच्या (मग ह्या राशी संख्येने कितीही असोत) घातांकसहित गुणाकार भागाकारानेच मांडता येतात आणि यामुळेच कोणतीही एकके वापरली, तरी दिलेल्या दोन वस्तूंच्या लांबीचे अगर घनफळाचे गुणोत्तर तेच रहाते.

राशीची परिमाण-सूत्र तयार झाली म्हणजे राशींची ओळख त्या सूत्रावरून करणे अथवा ठरविणे सोपे जाते. भौतिकशास्त्रातील घटनांत अथवा घडामोडींत कोणकोणत्या राशींचा अंतर्भाव होतो किंवा होऊ शकतो तसेच त्यांचा परस्पर संबंध काय असेल याविषयी पुष्कळ बरोबर अंदाज ‘परिमाण विश्लेषणाच्या’ पद्धतीमध्ये बांधता येतो. हा त्या पद्धतीचा मुख्य कार्यभाग आहे व तो फार उपयुक्त आहे. एखाद्या राशीच्या एका प्रकारच्या एककात व्यक्त केलेल्या समीकरणाच्या आधारे सहजपणे करता येते. तसेच भौतिकीय घटना अथवा नियम गणिती समीकरणात दोन्ही बाजूंची परिमाणे समान यावसाय हवी [→ परिमाणात्मक विश्लेषण].

कोणत्याही राशीच्या परिमाण-सूत्रात मूलभूत राशींचे घातांक शून्य, अधिक. उणे, पूर्णांक अथवा अपूर्णांक असू शकतात. विद्युत् चुंबकीय राशींच्या परिमाण-सूत्रांत घातांक विशेषेकरून अपूर्णांक असतात.

नेहमीच्या प्रचारातील एकके : वर उल्लेखल्याप्रमाणे ब्रिटिशांच्या स्वेच्छ मापन पद्धतीत लांबीचे एकक फूट आहे तथापि यार्ड, मैल ही मोठ्या मूल्यांची एककेही गरजेनुसार वापरतात. वस्तुमानाचे एकक पौंड आहे. हंड्रेडवेट अथवा टन अशी मोठी एककेही वापरतात. कालखंडाचे एकक सेकंद असून तो कालखंड एका माध्य (सरासरी) सौरदिनाचा १/८६४०० इतका भाग आहे. कोणत्याही लागोपाठच्या दोन मध्यान्ह समयातील कालखंड म्हणजे एक सौरदिन होय (परंतु पृथ्वीच्या गतीमधील अनियमितपणामुळे सेकंदाचीही व्याख्या हल्ली बदलण्यात आली आहे). दिनमान वर्षभरात बदलत असते, दिनमानाची एक वर्षाची सरासरी घेतली म्हणजे त्याला माध्य सौरदिन म्हणतात. कालाची मोठी एकके तास, दिवस वगैरे आहेतच. मेट्रिक पद्धतीत लांबीचे एकक सेंटिमीटर (मोठी एकके मीटर, किलोमीटर इ.) वस्तुमानाचे एकक सेकंद हे ब्रिटिश पद्धतीत धरल्याप्रमाणेच आहे.

प्रेरणेची एकके पौंडल (ब्रिटिश) व डाइन (मेट्रिक) अशी आहेत. कार्य व ऊर्जा यांचे मापन एकाच एककाने करतात कारण ऊर्जा म्हणजे कार्य करण्याची क्षमता होय. ब्रिटिश पद्धतीत कार्य अथवा ऊर्जा मोजण्याचे एकक फूट-पौंडल असे आहे. १ पौंडल प्रेरणेने तिच्याच दिशेने एखादी वस्तू १ फूट लांब ढकलली असता एक फूट-पौंडल इतके कार्य होते. मेट्रिक पद्धतीत कार्याचे अथवा ऊर्जेचे एकक ‘अर्ग’ आहे. १ डाइन या प्रेरणेने स्वतःच्याच दिशेने एखादी वस्तू १ सेंटिमीटर लंब ढकलली असता एक अर्ग इतके  कार्य होते. कार्यत्वरा म्हणजे दर सेकंदास झालेले कार्य. याच्या ब्रिटिश अथवा गुरुत्वीय मापन पद्धतीच्या आधारावर उभारलेल्या कार्यत्वरेच्या व्यावहारिक एककाला ‘हॉर्स पॉवर’ अथवा ‘अश्वशक्ती’ असे नाव आहे [→ अश्वशक्ति]. ब्रिटिशांच्या ‘गुरुत्वीय’ मापन पद्धतीत कार्य अथवा ऊर्जा यांचे एकक ‘फूट-पौंड’ असे आहे. दर सेकंदास ५५० फूट-पौंड कार्य होणे म्हणजे १ हॉर्स पॉवर अथवा १ अश्वशक्ती खर्ची घालणे अथवा तयार करणे होय. व्याख्येनुसर कार्यत्वरा (किंवा ऊर्जाक्षयवेग) म्हणजे प्रेरणा गुणिले वेग असतो. एम. के. एस. पद्धतीत लांबीचे एकक मीटर, वस्तुमानाचे किलोग्रॅम व कालाचे सेकंद असे गणले आहे. विसाव्या शतकाच्या सुरुवातीस जॉर्जी या फ्रेंच शास्त्रज्ञांनी या पद्धतीचा पुरस्कार केला व सध्या ही पद्धती विशेषतः अभियांत्रिकीत फार प्रचलित आहे. या पद्धतीत प्रेरणेच्या एककाचे नाव न्यूटन असे आहे. १ न्यूटन या प्रेरणेने १ किलोग्रॅम वस्तूत १ मीटर प्रती सेकंद इतका प्रवेग निर्माण होतो. व्याख्येनुसार १,००० ग्रॅम म्हणजे १ किलोग्रॅम व १ मीटर प्रती सेकंद-वर्ग प्रवेग म्हणजे १०० सेंमी. प्रती सेकंद-वर्ग प्रवेग असे प्रमाण असल्यामुळे १ न्यूटन प्रेरणा म्हणजे १ लक्ष डाइन होतात. तसेच १ न्यूटन प्रेरणेने तिच्याच दिशेने एखाद्या वस्तूचे १ मीटर स्थलांतर झाले म्हणजे जे कार्य होते त्या कार्याला १ जूल असे म्हणतात. जूल हे एम. के. एस. पद्धतीतले कार्याचे एकक होय. १०^७ अर्ग (म्हणजे एक कोटी अर्ग) म्हणजे १ जूल एवढे कार्य एका सेकंदात होत असेल, तर व्याख्येनुसार कार्यत्वरा १ वॉट होत असते. ७४६ वॉट म्हणजे १ अश्वशक्ती. असा या दोन कार्यत्वरेच्या एककांतील परस्पर संबंध आहे. वरील मापन पद्धतींशिवाय १९६० मध्ये आंतरराष्ट्रीय मानक संस्थेने मीटर, किलोग्रॅम, सेकंद, अँपिअर, अंश केल्व्हिन (तापमान) व कँडेला (दीप्ती घनता) अशा मूलभूत राशी घेऊन एका ‘एस आय’ (आंतररष्ट्रीय पद्धती) नामक पद्धतीचा पुरस्कार केला. भारतीय मानक संस्थेने तिचा १९६६ मध्ये स्वीकार केला आहे. ‘एस आय’ पद्धतीतील मूलभूत एकके, पूरक एकके व साधित एकके, कोष्टक क्र. ४ मध्ये दिली आहेत. कोष्टक क्र. १ मध्ये मूलभूत राशी व त्यांचे परस्परसंबंध दिले आहेत.

तापमान पद्धती : उष्णतेमुळे होणाऱ्या पदार्थातील प्रसरण किंवा इतर गुणधर्मांत होणार्‍या बदलावर तापमापकाची स्थापना केलेली असते. उदा., घन व द्रव पदार्थांतील उष्णतेमुळे होणारे  आकारमानातील फरक, वायुरूप पदार्थांत होणारे दाबातील व घनफळातील फरक किंवा धातूच्या विद्युत् रोधातील बदल वगैरे. तथापि यांपैकी कोणत्यातरी एका गुणधर्माचे शुद्ध बर्फाच्या वितळबिंदूच्या वेळी असलेले मूल्य जर क_वि आणि शुद्ध पाण्याच्या उकळबिंदूच्या वेळी असलेले मूल्य क_उ यांनी दर्शविले, तर त्याच गुणधर्माचे क_ता हे मूल्य ता हे तापमान असल्यावेळी आहे असे मानल्यास

ता	=	कता – कवि
१००		कउ – कवि

या समीकरणाने मिळते. हे समीकरण तापक्रमाचे पायाभूत समीकरण आहे. या समीकरणामुळे त्या गुणधर्माच्या आधारावर कोणतेही तापमान मूल्य ता काढता येते. उष्णतेमुळे होणाऱ्या इतर कोणत्याही

कोष्टक क्र. १ सामान्य भौतिकीतील काही एकके
राशी	सी. जी. एस. एकक	एम. के. एस. एकक	ब्रिटिश एकक	ब्रिटिश व सी. जी. एस. एककांचे गुणोत्तर
(१)    मूलभूत राशी          लांबी (लां)          वस्तुमान (व)         कालखंड (का)	सेंटिमीटर (सेंमी.) ग्रॅम (ग्रँ) सेकंद (से.)	मीटर (मी.) किलोग्रॅम (किग्रॅ.) सेकंद (से.)	फूट (फू.) पौंड (पौं.) सेकंद (से.)	३०·४८    ४५३·५९२३७         १·००००
(२)     पूरक राशी             कोन           घन कोन	रेडियन (अरियमान) (रे.)  स्टरेडियन (स्ट.)	—- —-	—- —-	—- —-
(३)     साधित राशी             क्षेत्रफळ             घनफळ             वेग             प्रवेग             प्रेरणा             दाब             कार्य, ऊर्जा             कार्यत्वरा	चौ. सेंमी. घ. सेंमी सेंमी. प्रती सेकंद सेंमी. प्रती सेकंद२  डाइन डाईन प्रती चौ. सेंमी.  अर्ग अर्ग प्रती सेकंद	चौ. मी. घ. मी. मी. प्रती सेकंद मी. प्रती सेकंद२ न्यूटन न्यूटन प्रती चौ.मी. जूल वॉट	चौ. फू. घ. फू. फू. प्रती सेकंद फू. प्रती सेकंद२ पौंडल पौंड प्रती चौ. इंच फूट-पौंडल अश्वशक्ती	९२९·०३०    २८·३१६ x १०३    ३०·४८    ३०·४८    १३·८२५५ x १०३       ६·८९४७६ x १०४     ४२·१४० x १०४     ७४५·७०० x १०७
ब्रिटिश गुरूत्वीय पद्धतीत वस्तुमानाचे एकक ‘स्लग’ आहे. १ स्लग = ३२·१७४ पौंड.

गुणधर्माच्या बदलाचा वरील समीकरणानुसार वापर करता येतो. परंतु त्यामुळे मिळणारे मापनक्रम समीकरणात उल्लेख केलेले दोन स्थिरबिंदू वगळून इतर तापमानं मूल्ये एकमेकांस तंतोतंत जुळतीलच असे नाही. वस्तूंच्या निरनिराळ्या गुणधर्मांच्या एकमेकांशी काही संबंध असतोच असे नाही, त्यामुळे पारा असलेला तापमापक, स्थिर घनफळ हायड्रोजन वायू तापमापक किंवा प्लॅटिनम विद्युत् रोध तापमापक यांत तंतोतंत जुळणी अथवा एकवाक्यता नसते. या नैसर्गिक व नेहमी आढळणाऱ्या अडचणींमुळे वरीलपैकी कोणतातरी एक सोईस्कर तापमापक प्रमाणभूत म्हणून धरणे अवश्य होते व त्याच्यासापेक्ष दुसरे अंशपरीक्षित तापमापक तयार करणे ओघानेच येते. स्थिर आयतन हायड्रोजन वायू तापमापक ‘मानक’ (प्रमाणभूत साधन) म्हणून गणला गेला आहे. तथापि उष्णतेमुळे पदार्थातील गुणधर्माच्या बदलावर अवलंबून न राहणारा तापक्रम मिळणे शक्य झाल्यास तो केव्हाही सर्वोत्कृष्ट ठरणार. ऊष्मागतिकीमध्ये (उष्णतेचा यांत्रिक व इतर स्वरूपांतील ऊर्जांशी असणाऱ्या संबंधाचे गणितीय विवेचन करणाऱ्या शास्त्रामध्ये) तापमानाची गणना उष्णतेमुळे बदलणाऱ्या पदार्थातील कोणत्याही गुणधर्मावर अवलंबून नसते, उष्णतेमुळे चालणाऱ्या काल्पनिक आदर्श एंजिनाच्या तात्त्विक विवेचनातून निर्माण झालेला एक केवल किंवा निरपेक्ष तापक्रम लॉर्ड केल्व्हिन यांनी रचला आहे. निरपेक्ष तापक्रमातील कोणत्याही दोन तापमानांचे गुणोत्तर, हे वरील मानक म्हणून धरलेल्या हायड्रोजन वायूच्या स्थिर घनफळ तापमापकाने मोजून आलेल्या तापमानाच्या गुणोत्तराएवढेच येते, हे सिद्ध झाले आहे. या दोन तापक्रमांचे शून्यांक जुळते करण्यात आले म्हणजे हे दोन तापक्रम एकमेकांशी अगदी तंतोतंत जुळतात. पूर्वीप्रमाणे बर्फाच्या वितळबिंदूच्याऐवजी (०^० से.) पाण्याच्या तीन अवस्थेतील (बर्फ, पाणी व वाफ) समतोल बिंदूचे (त्रिक-बिंदूचे) तापमान २७३·१६^० के. (K) मानक म्हणून स्वीकारण्यात आले आहे. तापमानाच्या वरील तापक्रमाशिवाय सेल्सिअस (पूर्वीचे सेंटिग्रेड), फॅरनहैट व रोमर हे तापक्रम त्या त्या गुणधर्माच्या बदलाचा वरील समीकरणानुसार वापर करता येतो. परंतु त्यामुळे मिळणारे मापनक्रम समीकरणात उल्लेख केलेले दोन स्थिरबिंदू वगळून इतर तापमानं मूल्ये एकमेकांस तंतोतंत जुळतीलच असे नाही. वस्तूंच्या निरनिराळ्या गुणधर्मांच्या एकमेकांशी काही संबंध असतोच असे नाही, त्यामुळे पारा असलेला तापमापक, स्थिर घनफळ हायड्रोजन वायू तापमापक किंवा प्लॅटिनम विद्युत् रोध तापमापक यांत तंतोतंत जुळणी अथवा एकवाक्यता नसते. या नैसर्गिक व नेहमी आढळणाऱ्या अडचणींमुळे वरीलपैकी कोणतातरी एक सोईस्कर तापमापक प्रमाणभूत म्हणून धरणे अवश्य होते व त्याच्यासापेक्ष दुसरे अंशपरीक्षित तापमापक तयार करणे ओघानेच येते. स्थिर आयतन हायड्रोजन वायू तापमापक ‘मानक’ (प्रमाणभूत साधन) म्हणून गणला गेला आहे. तथापि उष्णतेमुळे पदार्थातील गुणधर्माच्या बदलावर अवलंबून न राहणारा तापक्रम मिळणे शक्य झाल्यास तो केव्हाही सर्वोत्कृष्ट ठरणार. ऊष्मागतिकीमध्ये (उष्णतेचा यांत्रिक व इतर स्वरूपांतील ऊर्जांशी असणाऱ्या संबंधाचे गणितीय विवेचन करणाऱ्या शास्त्रामध्ये) तापमानाची गणना उष्णतेमुळे बदलणाऱ्या पदार्थातील कोणत्याही गुणधर्मावर अवलंबून नसते, उष्णतेमुळे चालणाऱ्या काल्पनिक आदर्श एंजिनाच्या तात्त्विक विवेचनातून निर्माण झालेला एक केवळ किंवा निरपेक्ष तापक्रम लॉर्ड केल्व्हिन यांनी रचला आहे. निरपेक्ष तापक्रमातील कोणत्याही दोन तापमानांचे गुणोत्तर, हे वरील मानक म्हणून धरलेल्या हायड्रोजन वायूच्या स्थिर घनफळ तापमापकाने मोजून आलेल्या तापमानाच्या गुणोत्तराएवढेच येते, हे सिद्ध झाले आहे. या दोन तापक्रमांचे शून्यांक जुळते करण्यात आले म्हणजे हे दोन तापक्रम एकमेकांशी अगदी तंतोतंत जुळतात. पूर्वीप्रमाणे बर्फाच्या वितळबिंदूच्याऐवजी (०^० से.) पाण्याच्य तीन अवस्थेतील (बर्फ, पाणी व वाफ) समतोल बिंदूचे (त्रिक-बिंदूचे) तापमान २७३·१६^० के. (K) मानक म्हणून स्वीकारण्यात आले आहे. तापमानाच्या वरील तापक्रमाशिवाय सेल्सिअस (पूर्वीचे सेंटिग्रेड), फॅरनहैट व रोमर हे तापक्रम त्या त्या नावाच्याशास्त्रज्ञांनी प्रचारात आणले. डॉक्टरांच्या तापमापकात व अभियांत्रिकीमध्ये काही ठिकाणी फॅरनहैट तापक्रम वापरतात. मात्र रोमर तापक्रम फारसा वापरात नाही.

आंतरराष्ट्रीय तापक्रम प्रथम १९२८ साली प्रचलित झाला व नंतर पुन्हा १९४८ व १९५४ साली त्यात थोडा बदल होऊन आता सर्वत्र मान्यता पावला आहे.

आंतरराष्ट्रीय तापक्रम

आंतरराष्ट्रीय सेल्सिअस तापमान त^० से.  → आंतरराष्ट्रीय केल्व्हिन तापमान ट^० के. या रूपांतराचे सूत्र खालीलप्रमाणे आहे :

ट^० के. = (त^० + २७३·१६^०) से.

                                                                                                           दर्शकचिन्ह ^० के. } दर्शकचिन्ह ^० से.                                                                                                                                                                                                                          अंश केल्व्हिन      अंश सेल्सिअस

१९४८ साली भरलेल्या आंतरराष्ट्रीय वजने व मापे समितीच्या परिषदेतील ठरावानुसार पूर्वी ज्या तापक्रमाला सेंटिग्रेड म्हणत असत त्याला आता सेल्सिअस हे नाव देण्यात आले आहे. आंतरराष्ट्रीय तापक्रमाचे ऊष्मागतिकीय तापक्रम व व्यावहारिक तापक्रम असे दोन प्रकार आहेत. परंतु त्या दोहोंतील फरक इतका सूक्ष्म आहे की त्याचे अद्याप मूल्यमापनच करता आलेले नाही [→ तापमापन केल्व्हिन निरपेक्ष तापक्रम ऊष्मागतिकी].

प्रकाश, प्रारण, ध्वनी इत्यादिकांची मापके-एकके : प्रकाश ही एक प्रकारची प्रारण ऊर्जाच (तरंगरूपी ऊर्जाच) असल्याने त्याच्या मापनासाठी ऊर्जेच्याच एककांचा वापर का करू नये असे प्रथमदर्शनी वाटेल. परंतु आपल्या डोळ्यांची संवेदनक्षमता वेगवेगळ्या रंगाच्या प्रकाशाला वेगवेगळी असते आणि प्रकाशमापनात ऊर्जेच्या मापनापेक्षा त्या प्रकाशाची मानवी नेत्राला प्रतीत होणारी तेजस्विता (चकासन) मोजणे जास्त महत्त्वाचे आहे. नेत्राला प्रतीत होणाऱ्या प्रकाशाला यापुढे ‘नेत्रग्राह्यप्रकाश’ अशी संज्ञा दिली आहे.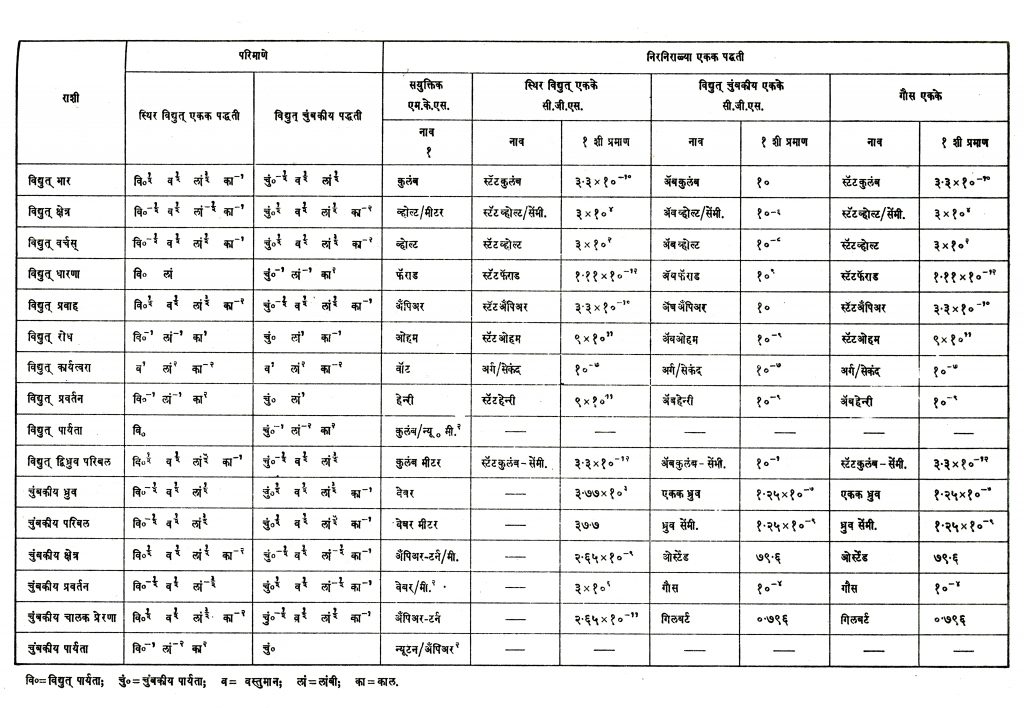

नेत्रग्राह्यप्रकाशाच्या मापनासाठी कँडेला हे एक नवीन मूलभूत एकक स्वीकारणे भाग पडते. कोणत्याही प्रकाश-उगमाची (विशिष्ट दिशेने) नेत्रग्राह्यप्रकाश देण्याची क्षमता म्हणजेच त्या प्रकाश-उगमाची (त्या दिशेची) दीप्ती होय. कँडेला हे दीप्ती मोजण्याचे एकक असून १९३७ साली भरलेल्या आंतरराष्ट्रीय परिषदेने कँडिलाची व्याख्या पुढीलप्रमाणने निश्चित केली आहे : एखादा पूर्ण प्रारण-उगम (सर्व प्रकारचे प्रारण उत्सर्जित करणारा उगम) द्रव प्लॅटिनम धातूच्या घनीभवनाच्या (घन स्थितीत जाण्याच्या) तापमानाला तापविला असता त्याच्या पृष्ठभागावरील एक चौरस सेंटिमीटर क्षेत्रफळाची दीप्ती-तीव्रता लंब दिशेने एक कँडेलाच्या साठपट असते. दीप्तीचे मूळ एकक कँडल हे होते. त्यावरून कँडल पॉवर हा शब्दप्रयोग रूढ झाल. कँडल म्हणजे मेणबत्ती. मेणबत्तीचे दीप्तिमान अगदी पूर्णपणे स्थिर राहू शकत नाही म्हणून हे नवीन एकक अंगिकारण्यात आले.

एखाद्या कारंजाच्या तोटीमधून पाणी बाहेर फेकले जाते तद्वत प्रकाश-उगमातून सर्व बाजूने प्रकाशाचा प्रवाह बाहेर येत असतो. या नेत्रग्राह्यप्रकाशाच्या प्रवाहाला ‘दीप्ती-स्रोत’ ही संज्ञा आहे व तो मोजण्याचे एकक ‘ल्यूमेन’ हे आहे. एक कँडेला दीप्तीच्या बिंदुमात्र प्रकाश-उगमापासून एक स्टरेडियन घन कोनातून सोडला जाणारा दीप्ती-स्रोत एक ल्यूमेन असतो व क कँडेला दीप्तीच्या प्रकाश-उगमापासून बाहेर पडणारा एकूण दीप्ती-स्रोत ४ π क ल्यूमेन भरेल. एखादा पृष्ठभाग कितपत प्रकाशित झाला आहे, हे त्या पृष्ठाच्या प्रति-एकक क्षेत्रफळावर पडणार्‍या दीप्ती-स्रोतावर म्हणजेच प्रकाश तीव्रतेवर अवलंबून असते. एम. के. एस. पद्धतीतील प्रकाश तीव्रतेचे एकक ‘लक्स’ आहे. जेव्हा एखाद्या पृष्ठावर प्रती चौ. मी. क्षेत्रावर एक ल्यूमेन दीप्ती-स्रोत पडत असेल तेव्हा त्या पृष्ठाचे ‘प्रकाशन’ एक लक्स आहे, असे मानण्यात येते. ब्रिटिश पद्धतीतले प्रकाशनाचे एकक फूट-कँडल हे आहे. १ फूट-कँडल = १ ल्यूमेन प्रती चौरस फूट. सी. जी. एस. पद्धतीतील प्रकाशनाचे एकक फॉट आहे. १ फॉट = १०^४ लक्स. पृष्ठाची तेजस्विता एम. के. एस. पद्धतीत ‘निट’ व सी. जी. ए. पद्धतीत ‘स्टिल्ब’ या एककांनी मोजण्यात येते [→ प्रकाशमापन].

ध्वनिविषयक एकके : सर्व साधारणपणे २० ते २०,००० हर्ट्‌झ (१ हर्ट्‌झ = प्रती सेकंदाला १ कंपन) एवढ्या कंप्रतेचे (दर सेकंदाला होणार्‍या कंपन संख्येचे) आवाज मानवी कानाला ऐकू येतात. ध्वनिविषयक मोजावयाच्या राशी म्हणजे (१) कंप्रता, (२) स्वराची उच्चनीचता किंवा स्वरपद, (३) तीव्रता व (४) गरिमा ह्या होत. कंप्रतेचे एकक हर्ट्‌झ हे असून त्याचे मूल्य वर दिलेले आहे. कंप्रता वाढली की, कानाला ध्वनी जास्त उच्च वाटतो. ह्या उलट कंप्रता कमी झाली की, ध्वनी नीच वाटतो. कानाला प्रतीत होणारी ही उच्चनीचता कंप्रतेच्या लॉगरिथमाच्या प्रमाणात असते व तिच्या मापनासाठी ‘मेल’ हे एकक वापरतात. सर्व मापनासाठी १,००० हर्ट्‌झ कंप्रतेचा ध्वनी हा मानक म्हणून वापरला जातो ह्या ध्वनीचे स्वरपद १,००० मेल आहे. विशिष्ट ठिकाणी ध्वनीच्या तरंगांमुळे प्रती चौरस सेंमी. वर प्रती सेकंदाला पडणारी ध्वनि-ऊर्जा म्हणजे तेथील ध्वनीची तीव्रता होय. दोन ध्वनींच्या तीव्रतेतील फरक फ मोजण्याचे एकक डेसीबेल आहे. त्या दोन ध्वनींची तीव्रता अनुक्रमे ती_१ व ती_२ असल्यास, त्यांच्यातील फरक फ डेसीबेल पुढील समीकरणाने दिला जातो :

फ = १० X लॉग_१०^ती_१/_ती२

बेल हे एकक डेसीबेलच्या दहापट मोठे आहे. ध्वनीची गरिमा ‘फॉन’या एककाने मोजतात. दिलेल्या ध्वनीइतक्याच गरिमेच्या मानक ध्वनीची तीव्रता ती डेसीबेल असल्यास, दिलेल्या ध्वनीची गरिमा ती फॉन असते [→ ध्वनि].

प्रारणाची एकके : प्रकाश, ध्वनी, उष्णता व विद्युत् चुंबकीय ऊर्जेच्या प्रारणाचे एकक म्हणजे प्रती सेकंदास व प्रती एकक क्षेत्रफळावर पडलेली त्या त्या प्रकारची ऊर्जा होय. मागे उल्लेख केल्याप्रमाणे ‘वॉट’ प्रती चौरस सेंमी. या एककामध्ये तिचे मापन केले जाते.

विद्युत् चुंबकीय राशींच्या मापनासाठी एकके, त्यांची परिमाणे व एकक पद्धतींतील परस्पर संबंध : विद्युत् राशी : दोन भिन्न मूल्यांचे (अथवा समान मूल्यांचे) विद्युत् भार काही अंतरावर हवेत अथवा कोणत्याही माध्यमात ठेवले असता त्यांच्यात आढळून येणारे आकर्षण अथवा प्रतिसारण यासंबंधी कुलंब या शास्त्रज्ञांनी प्रायोगिकरीत्या एक सिद्धांत बसवला. या सिद्धांताच्या मदतीने व व्याख्यारूपाने सर्व विद्युत् राशींची एकके व परिमाणे काढता येतात.

सर्व विद्युत् राशींवर माध्यमाच्या मूलभूत गुणधर्मांचा परिणाम होतो. या मूलभूत गुणधर्मास पार्यता म्हणतात. निर्वातावस्थेची विद्युत् पार्यता वि_० या चिन्हाने दर्शविल्यास प्रमुख विद्युत् राशींची मापने, प्रेरणा या महत्त्वाच्या राशीवर अवलंबून असल्यामुळे, अखेर विद्युत् पार्यता (वि_०), लांबी (लां), वस्तुमान (व) आणि काल (का) या मूलभूत राशींच्या भाषेत मांडता येतात. चटकन लक्षात येणारी गोष्ट ही की, राशींची परिमाणे म्हणजेच मूलभूत राशींच्या भाषेत मांडता येतात. चटकन लक्षात येणारी गोष्ट ही की, राशींची परिमाणे म्हणजेच मूलभूत राशींचे घातांक अपूर्णांकही असतात. अशा तऱ्हेने बसविलेल्या एकक पद्धतीस ‘स्थिर विद्युत् एकक’ (इलेक्ट्रो स्टॅटिक यूनिट, इ. एस. यू.) पद्धती म्हणतात. काही विद्युत् व चुंबकीय राशींची निरनिराळ्या एकक पद्धतींतील एकके, त्यांची नावे, परिमाणे व परस्पर संबंध कोष्टक क्र. २ मध्ये दिले आहेत.

चुंबकीय राशी : दोन भिन्न मूल्यांचे (अथवा समान मूल्यांचे) चुंबकीय ध्रुव काही अंतरावर हवेत अथवा कोणत्याही माध्यमात ठेवले असता त्यांच्यात आढळून येणारे आकर्षण अथवा प्रतिसारण यासंबंधीही कुलंब यांनीच प्रायोगिकरीत्या एक सिद्धांत बसवला आहे. त्या सिद्धांताच्या मदतीने व व्याख्यारूपाने सर्व चुंबकीय राशींची एकके व परिमाणे काढता येतात. सर्व चुंबकीय राशींवर माध्यमाच्या एका मूलभूत गुणधर्माचा परिणाम होतो. या मूलभूत गुणधर्मास माध्यमाची चुंबकीय पार्यता म्हणतात. निर्वातावस्थेच्या चुंबकीय पार्यतेचे मूल्य चुं_० या चिन्हाने दर्शविल्यास, प्रमुख चुंबकीय राशींच्या मापनाची एकके व परिमाणे अखेर चुंबकीय पार्यता (चुं_०), लांबी (लां), वस्तुमान (व) आणि काल (का) या मूलभूत राशींच्या भाषेत मांडता येतात. येथेही चटकन लक्षात भरणारी गोष्ट म्हणजे त्या राशींची परिमाणे म्हणजेच चुंबकीय पार्यतेसह मूलभूत राशींचे घातांक बहुधा अपूर्णांक असतात. या एकक पद्धतीला विद्युत् चुंबकीय एकके (इलेक्ट्रो मॅग्‍नेटिक यूनिट, इ. एम. यू.) पद्धती असे नाव आहे. खालील उदाहरणावरून या राशींची परिमाणे कशी काढतात याची स्पष्ट कल्पना येईल. ध्रु या बलाचे दोन चुंबकीय ध्रुव निर्वातात एकमेकांपासून स या अंतरावर ठेवल्यास त्यांच्यामधील प्रे ही प्रेरणा पुढील समीकरणाने दिली जाते :

प्रे =	ध्रु२	; ध्रु२ = प्रे x चुं० x स२
	चुं० x स२

[ध्रु] = चुं_० ^१/२x लां ^३/२x व ^१/२x का–^१

 वरील दोन एकक पद्धतींतील परस्पर संबंध : स्थिर विद्युत् राशींचा विचार तसाच चुंबकीय राशींचा विचार वेगवेगळ्या व स्वतंत्ररीत्या केला, तर विद्युत् भार आणि चुंबकीय ध्रुव तसेच विद्युत् आणि चुंबकीय पार्यता या दोन जोड्यांत कोणताही सैद्धंतिक वा व्यावहारिक संबंध जोडता येत नाही. पण स्थिर विद्युत् प्रवाही झाली म्हणजे विद्युत् प्रवाह निर्माण होतो व मग त्याचा चुंबकीय ध्रुवावर परिणाम होतो. तेव्हा वरील दोन जोड्यांत काही तरी संबंध असलाच पाहिजे, हा निष्कर्ष निघतो. विद्युत् प्रवाहामुळे (उदा., सरळ संवाहकातून जाणाऱ्या प्रवाहामुळे) चुंबकीय ध्रुवावर कार्या न्वित होणारी प्रेरणा लाप्लस-अँ पिअर सिद्धांतानुसार काढता येते व त्यावरून वरील जोड्यांमध्ये खाली दाखविल्याप्रमाणे संबंध आहे हे आढळून येते.

वि_०^१/२x चुं_०^१/२ म्हणजे विद्युत् पाऱ्याता व चुंबकीय पार्यता यांच्या गुणाकाराच्या वर्गमूळाची परिमाणे बरोबर वेगाच्या व्यस्ताकांच्या परिमाणाइतकी येतात. १/√ वि_० x चुं_० या पदाचे मूल्य प्रायोगिकरीत्या काढता येते व वरील विवेचनानुसार या पदाची परिमाणे वेगराशीचीच असतात. चुं_० किंवा वि_० या निर्वाताच्या गुणधर्माची मूल्ये स्वेच्छेनुसार व सोईनुसार खाली  दाखविल्याप्रमाणे धरली , तर त्यामुळे ‘स्थिर विद्युत् एकक’ व ‘विद्युत् चुंबकीय एकक’ या एकक पद्धती कशा तयार हो तात, हे दिसून येईल. उदा., वि_० = १ धरले, तर चुं = ^१ / वेग_२ झाल्यामुळे स्थिर विद्युत् एकक पद्धती तयार होते. याउलट चुं_० = १ धरले तर वि_० = ^१ / वेग_२ झाल्यामुळे विद्युत् चुंबकीय एकक पद्धती तयार होते. पुष्कळ वेळा विद्युत् राशी स्थिर विद्युत् एककात मांडतात आणि चुंबकीय राशी विद्युत्  चुंबकीय एककात मांडतात. पण जेव्हा दोन्ही राशींचा संबंध समीकरणरूपाने जोडता येतो तेव्हा वि_०= १ आणि चुं_० = १ धरले, तर त्यातून तयार होणाऱ्या एकक पद्धतीस ‘गौस एकक पद्धती’ म्हणतात. आता १/√ वि_० x चुं_०याचे मूल्य म्हणजेच प्रकाश वेग असतो हे सैद्धां तिक तसेच प्रायोगिकरीत्याही सिद्ध झाले आहे.

व्यावहारिक (सी. जी. एस. – इ. एम. यू.) एकक पद्धती : विद्युत् चुंबकीय व विद्युत् चुंबकीय राशींच्या एककास संशोधकांचीच नावे त्यांच्या सन्मानार्थ दिली आहेत व त्यांच्या व्याख्याही  केलेल्या आहेत. वरील तीन एकक पद्धतीं तील तत्सम राशींचे परस्परसंबंध काय आहेत, हेही पूर्णपणे दाखविण्यात आले आहेत (पहा कोष्टक क्र.२). व्यावहारिक एकक पद्धतीत कोणत्या राशीच्या एककाचे नाव काय आहे याचे कोष्टक खाली दिले आहे :

कोष्टक क्र. ३. व्यावहारिक एकक पद्धतीतील विद्युत्‌ व चुंबकीय एकके
राशीचे नाव	एककाचे नाव
विद्युत्‌ भार	कुलंब
विद्युत्‌ चालक प्रेरणा (वि. चा. प्रे.)	व्होल्ट
विद्युत्‌ प्रवाह	अँपिअर
विद्युत्‌ रोध	ओहम
विद्युत् धारणा	फॅराड
विद्युत्‌ प्रवर्तकत्व	हेन्‍री
चुंबकीय क्षेत्र	ओर्स्टेड (पूर्वी ‘गौस’)
चुंबकीय स्राोत	वेबर (पूर्वी ‘मॅक्सवेल’)
विद्युत्‌ ऊर्जा	जूल
शक्ती (कांर्यत्वरा)	वॉट

मीटर-किलोगॅम-सेकंद (एम. के. एस.) पद्धतीतील एकके : वरील एकक पद्धतींशिवाय मीटर, किलोग्रॅम, सेकंद व व्यावहारिक विद्युत् भार वा विद्युत् प्रवाहाचे अथवा विद्युत् रोधाचे एकक यांपैकी कोणते तरी एक अशा चार मूलभूत राशी धरून इतर सर्व राशींची एकके व्याक्येनुसार काढणाऱ्या एकक पद्धतीस एम. के. एस. पद्धती म्हणतात. ही एकक पद्धती जॉर्ज या फ्रेंच शास्त्रज्ञांनी १९०४ साली मांडली.

मागे उल्लेख केल्याप्रमाणे प्रेरणेच्या एककाचे नाव न्यूटन असून त्याचे मूल्य सी. जी. एस. पद्धतींतील एककाच्या एक लाखपट असते. या पद्धतीत कुलंब यांचे विद्युत् व चुंबकीय सिद्धांत खाली लप्रमाणे मांडले जातात:

(१) प्रे =	भा१ x भा२	, (२) प्रे =	ध्रु१ x ध्रु२
	वि० x स		चुं० x स

प्रे = प्रेरणा; भा_१ = विद्युत् भाराचे बल; भा_२ = दुसऱ्या विद्युत् भाराचे बल; ध्रु_१ = चुंबकीय ध्रुवाचे बल; ध्रु_२ = दुसऱ्या चुंबकीय ध्रुवाचे बल; वि_० = निर्वाताची विद्युत् पार्यता; चुं_० = निर्वाताची चुबकीय पार्यता; स = भा_१ व भा_२ यांमधील किंवा ध्रु_१ व ध्रु_२ मधील असणारे अंतर; प्रेरणेचे एकक न्यूटन; भा_१ व भा_२ यांचे एकक कुलंब आणि स चे मी टर असल्यामुळे व वि_० X चुं_० = १/प्रकाश-वेग^२ असल्यामुळे वि_० = १/९ X १०^९ फॅराड/मीटर होते. त्याचप्रमाणे चुं_० = १/१X१०^७ हेन्‍री/मीटर येते. वरील सिद्धां त आधारभूत धरल्यामुळे अनेक विद्युत् व चुंबकीय राशीं च्या मापनां त अतार्किकपणे ४π व २π हे गुणक येतात.

वस्तुतः गोलीय, चित्याकृती (दंडगोलाकृती) आणि अरीय (त्रिज्यीय) सममितीत (प्रमाणबद्धतेत) वरील गुणक येणे सकारण अथवा तर्कास धरून आहे, पण अशा सममिती नसलेल्या ठिकाणी वरील गुणक येणे तर्कास धरून नाही. म्हणून वरील मापन पद्धतीस अतार्किक एम. के. एस. पद्धती म्हणण्यात येते. हेव्हिसाइड या शास्त्रज्ञांनी वर उल्लेखलेल्या सममितीतच फक्त वरील गुणक ठेवून विद्युत् व चुंबकीय राशींच्या पुनर्व्याख्या कराव्यात असे सुचविले. अशा दृष्टीने तयार झालेल्या एकक पद्धतीस संयुक्तिक व्यावहारिक एम. के. एस. पद्धती म्हणतात. थोडक्यात म्हणजे गोलीय, चित्याकृती किंवा अरीय सममिती नाही, तेथे वरील गुणकांचा समावेश न करणे म्हणजे मापनात ‘सयुक्तिकता’ आणणे होय. या सयुक्तिक व्यावहारिक (हेव्हिसाइड) एम. के. एस. पद्धतीमध्ये

वि_० = ८·८५४ × १०^–१२ फॅराड/मीटर.

तसेच चुं_० ४ = ४ π × १०^–७ हेन्‍री/मीटर.

आंतरराष्ट्रीय एकके : विद्युत् मापनाची उपकरणे बनविणारांना विद्युत् प्रवाह किंवा विद्युत् वर्चस् (विद्युत् स्थिती) यांच्या मूळ व्याख्या सोईस्कर नाहीत. म्हणून आंतरराष्ट्रीय एकके निर्माण करण्यात आली. आजही ॲमीटर, व्होल्टमीटर यांसारख्या मापन यंत्रांचे मानकीकरण (प्रमाणीकरण) आंतरराष्ट्रीय एककांच्या संदर्भातच केलेले असते. १९४८ नंतर आंतरराष्ट्रीय एकेके वापरू नयेत असे ठरले व नवीन शुद्ध-एकके बनविण्यात आली. पूर्वीच्या काही आंतरराष्ट्रीय एककांची व आता नवीन निर्णयानुसार प्रमाणभूत धरलेल्या शुद्ध-एककांची गुणोत्तरे (किंवा एकमेकांशी असलेली प्रमाणे) खाली दिली आहेत.

(१)	आंतरराष्ट्रीय रोध ओहम	= १·०००४९
	शुद्ध रोध ओहम
(२)	आं. रा. अँपिअर	= ०·९९९८५
	शुद्ध अँपिअर
(३)	आं. रा. व्होल्ट	= १·०००३४
	शुद्ध व्होल्ट
(४)	आं. रा. वॉट	= १·०००१९
	शुद्ध वॉट

अणुकेंद्रीय भौतिकीची एकके : इलेक्ट्रॉन-व्होल्ट (ev) : एक इलेक्ट्रॉन म्हणजे १ व्होल्ट वर्चसाचा फरक असलेल्या दोन बिंदूतून जात असताना एका इलेक्ट्रॉनावर झालेले कार्य होय.

१ इलेक्ट्रॉन व्होट (ev) = १·६०२०३ X १०^-१२ अर्ग.

आणवीय द्रव्यमान एकक (ए.एम.यू.) : अणूचा भार हा ग्रॅममध्ये

कोष्टक क्र. ४ (अ). आंतरराष्ट्रीय एकक पद्धती : मूलभूत एकके
भौतिक राशी	एककाचे नाव	मराठी चिन्ह	आंतरराष्ट्रीय वापरात असलेले चिन्ह
लांबी	मीटर	मी.	m
वस्तुमान	किलोग्रॅम	किग्रॅ.	kg
काल	सेकंद	से.	s
विद्युत्‌ प्रवाह	अँपिअर	अँपि.	A
ऊष्मागतिकीय तापमान	अंश केल्व्हिन	के.	K
दीप्ती तीव्रता	कँडेला	कँ.	cd

१९६७ सालापासून तापमानाचा उल्लेख करताना ^० हे चिन्ह द्यावयाचे नाही उदा., १०^० के. असे न मांडता १० के. असे मांडावे, असे ठरविण्यात आले आहे.

कोष्टक क्र. ४ (आ). आंतरराष्ट्रीय एकक पद्धती : पूरक एकके प्रतल कोन व घन कोन घेतली आहेत त्यांची नावे व चिन्हे पुढीलप्रमाणे आहेत.
भौतिक राशी	एककाचे नाव	मराठी चिन्ह	आंतरराष्ट्रीय वापरात असलेले चिन्ह
प्रतल कोन	रेडियन (अरियमान)	रे.	rad
घन कोन	स्टरेडियन	स्ट.	sr

कोष्टक क्र. ४ (इ). आंतरराष्ट्रीय एकक पद्धती : काही साधित एकके आणि त्यांचे नावे व चिन्हे.
भौतिक राशी	एककाचे नाव	मराठी चिन्ह	आंतरराष्ट्रीय वापरात असलेले चिन्ह
प्रेरणा	न्यूटन	न्यू.	N
कार्य, ऊर्जा, उष्णता राशी	जूल, न्यूटन-मीटर, वॉट-सेकंद	जे.	J, N m, Ws
शक्ती	वॉट, जूल प्रती सेकंद	वॉ.	W, J/s
विद्युत्‌ भार	कुलंब	कु.	C
विद्युत्‌ चालक प्रेरणा	व्होल्ट	व्हो.	V, W/A
विद्युत्‌ धारणा	फॅराड	फॅ.	F, A s/V
विद्युत्‌ रोध	ओहम	ओ.	Ω, V/A
चुंबकीय स्त्रोत	वेबर	वे	Wb, Vs
चुंबकीय स्त्रोत घनता	टेस्ला, वेबर प्रती चौ. मी.	टे.	T, Wb/m2
प्रवर्तकता	हेन्‍री	हे	H, V s/A
दीप्ती स्त्रोत	ल्यूमेन	ल्यू.	lm
प्रकाशन	लक्स, ल्यूमेन प्रती चौ. मी.	ल.	lx, lm/m3

क्वचितच दर्शविला जातो. अणूचे व अणुकेंद्राचे द्रव्यमान मोजण्यासाठी आणवीय द्रव्यमान एकक या खास एककाचा उपयोग केला जातो. पूर्वी १ ए. एम. यू. = ऑक्सिजन अणूच्या वस्तुमानाचा ^१/_१६ भाग ही व्याख्या प्रचारात होती. परंतु ऑक्सिजनाचे तीन समस्थानिक (एकच अणुक्रमांक पण भिन्न अणुभार असलेले त्याच मूलद्रव्याचे प्रकार) असल्यामुळे रसायनशास्त्र व भौतिकी यांमध्ये अणुभार वेगवेगळे येत. हे घोटाळे टाळण्यासाठी १९६१ सालापासून ए. एम. यू.ची पुढील व्याख्या नव्याने करण्यात आली आहे :

१ ए. एम. यू. = कार्बन (१२) या अणूच्या वस्तुमानाचा ^१/_१२ भाग;

१ ए. एम. यू. = १·६६०३५ X १०^–२४ ग्रॅम [→ अणुभार; आणवीय द्रव्यमान एकक].

किरणोत्सर्ग मोजण्याची एकके : कोणत्याही किरणोत्सर्गी (कण वा किरण बाहेर टाकणार्‍या)मूलद्रव्याचे प्रती सेकंदाला ३·७०० × १०^१० इतक्या अणूंचे विघटन (फुटण्याची क्रिया) होत असेल, तर त्या द्रव्याचा किरणोत्सर्ग एक क्यूरी आहे, असे म्हणतात. ह्याच प्रकारचे रदरफर्ड ह्या नावाचे एकक सुचविले गेले होते पण हल्ली ते वापरात नाही [→ किरणोत्सर्गी].

क्ष-व गॅमा-किरण : हे किरण म्हणजे विद्युत् चुंबकीय तरंग होत. ह्यांची तरंगलांबी फारच लहान असल्यामुळे ती अँगस्ट्रॉम या एककात मोजली जाते. १ अँगस्ट्रॉम = १०^-८ सेंमी.

क्ष-किरण किंवा गॅमा-किरण यांचा वस्तूवरील माऱ्याचा प्रभाव मोजण्यासाठी राँटगेन हे एकक वापरतात. तर त्या किरणांचा जीवसृष्टीवरील परिणाम मोजण्यासाठी रेम हे एकक वापरतात [→ क्ष-किरण; किरणोत्सर्ग].

पहा : कालमापन; मेट्रिक पद्धति; लांबी, क्षेत्रफळ व घनफळ यांची एकके; वजने व मापे.

संदर्भ : Ipsen, D. C. Units, Dimensions and Dimensional Numbers, New York, 1962.

टोळे, मा. ग.