उष्णता प्रारण

उष्णता प्रारण : उष्णतेचे संक्रमण संवहन,संनयन व प्रारण या तीन प्रकारांनी होते. उष्णता संवहनाच्या क्रियेमध्ये उष्णता एका अणूपासून दुसर्‍या अणूला, दुसर्‍यापासून तिसर्‍याला, अशी मिळत जाऊन उष्णतेचे संक्रमण होते [→ उष्णता संवहन ]. या क्रियेमध्ये अणू (वा रेणू) आपली जागा प्रत्यक्ष सोडीत नाहीत. उष्णता संवहन प्रामुख्याने घन माध्यमात होते. माध्यम जर द्रव अथवा वायुरूप असेल तर माध्यमाचे अणू (वा रेणू) उष्णता वाहून नेतात व त्यामुळे उष्णतेचे संक्रमण होते. संक्रमणाच्या या प्रकाराला ‘उष्णता संनयन’ असे म्हणतात. [→ उष्णता संनयन]. द्रव्य माध्यमाशिवाय होणार्‍या संक्रमणाला ‘उष्णता प्रारण’ असे म्हणतात. सूर्यापासून निघालेली उष्णता पोकळीतून प्रवास करून पृथ्वीच्या वातावरणात शिरते, ती प्रारणामुळेच. एखाद्या उष्ण भट्टीजवळ उभे राहिल्यास उष्णता जाणवते ती प्रारणामुळेच.

उष्णता प्रारण हे घन, द्रव वा वायू पदार्थापासून, त्यांच्या तापमानामुळे तरंगरूपी ऊर्जेच्या स्वरूपात बाहेर टाकले जाते. हे उष्णता तरंग विद्युत् चुंबकीय तरंगच असतात. मॅक्सवेल यांच्या सिद्धांताप्रमाणे विद्युत् चुंबकीय क्षेत्रांचा परिणाम म्हणून तरंग निर्माण होतात अशा तरंगांच्या प्रसाराची दिशा, विद्युत क्षेत्र व चुंबकीय क्षेत्र एकमेकांशी काटकोन करतात. वास्तविक उष्णता प्रारणाच्या विस्तारात सर्व विद्युत्‌ चुंबकीय वर्णपटाचा म्हणजे रेडिओ तरंगांपासून ते अवरक्त (दृश्य वर्णपटातील तांबड्या रंगाच्या अलीकडील) किरण, दृश्य प्रकाश, जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील) किरण, क्ष-किरण व गॅमा किरण (अंत्यंत लहान तरंगलांबीचे विद्युत् चुंबकीय तरंग) यांच्यापर्यंतच्या भागांचा समावेश होतो. तथापि पृथ्वीवरील बहुतेक उष्ण पदार्थापासून मिळणारे उष्णता प्रारण बहुशः अवरक्त भागातीलच असते. तार्‍याचे तापमान त्या मानाने अत्युच्च असल्यामुळे त्यांच्या तापमानानुसार त्यांच्यापासून मिळणार्‍या प्रारणाच्या वर्णपटाचा विस्तार कमीअधिक असतो.

उष्णता प्रारणाचा शोध प्रथम हर्शेल यांनी सन १८०० मध्ये लावला. एका वर्णपटदर्शकाच्या (प्रकाशातील निरनिराळ्या रंगाच्या तरंगलांबीदर्शक रेषा दाखविणार्‍या साधनाच्या) प्रयोगामध्ये त्यांनी तापमापकाचा काळा केलेला फुगा वर्णपटातील रक्तवर्णाच्या अलीकडे ठेवला, तेव्हा त्यांना तापमापकाच्या नोंदीवरून तापमान वाढत असल्याचे दिसले. यावरून त्या जागी रक्तवर्णापेक्षा अधिक लांबीचे तरंग अस्तित्वात असले पाहिजेत, असे अनुमान त्यांनी बांधले, या अदृश्य तरंगांना इन्फ्रारेड (अवरक्त) किरण अशी संज्ञा त्यांनी दिली. उष्णता प्रारणाचे मापन (१) क्रुक्स यांचा प्रारणमापक, (२) लेस्ली यांचा भेददर्शी हवा तापमापक, (३) लँग्‍ली यांचा बोलोमीटर (विद्युत् गुणधर्माचा उपयोग करून प्रारण किंवा तापमान मोजण्याने साधन), (४) बॉइज यांचा प्रारण सूक्ष्ममापक, (५) तपचिती (उष्णतेचे सरळ विद्युत् ऊर्जेत रूपांतर करणारे एक साधन), (६) प्रारण उत्तापमापक (दूर अंतरावरून उच्च तापमान मोजणारे उपकरण) वगैरे उपकरणांनी करता येते. उष्णता प्रारणाला काच अपारदर्शक असल्यामुळे त्याचे पृथक्करण करण्यासाठी जो वर्णपटमापक वापरतात, त्यामध्ये काचेच्या लोलकाऐवजी पोटॅशियम ब्रोमाइड, सोडियम क्लोराइड (सैंधव, रॉक सॉल्ट), सिझियम आयोडाइड यांसारख्या पदार्थांच्या स्फटिकांचा लोलक वापरतात. तसेच काचेच्या भिंगाऐवजी धातूंचे अंतर्गोल परावर्तक वापरतात.

प्लांक यांच्या पुंज सिद्धांताप्रमाणे [→ पुंज क्षेत्र सिद्धांत] प्रारण ऊर्जा अखंड स्वरूपात नसून ती अलग अशा पुंजांच्या (क्कांटमांच्या) स्वरूपात असते.

उष्णता तरंग व प्रकाश तरंग यांचे, त्यांच्या तरंगलांबीतील फरक सोडून,बाकी सर्वच बाबतीत साम्य आहे. उष्णता तरंग प्रकाशाप्रमाणेच सरळ रेषेत प्रवास करतात त्यांचा वेग प्रकाशाइतकाच म्हणजे दर सेकंदाला २·९९८ × १०^१० सेंमी इतका असतो, त्यांचे परावर्तन, प्रणमन (प्रकाश किरणांचे एका माध्यमातून दुसर्‍या माध्यमात दिशा बदलून जाणे, वक्रीभवन), व्यतिकरण (दोन किंवा अधिक तरंगमालिका एकमेकांवर येऊन पडतात तेव्हा अशा ठिकाणी घडून येणारा आविष्कार प्रकाश तरंगांत अशा ठिकाणी काळेपांढरे किंवा रंगीत पट्टे दिसतात.) विवर्तन (अपारदर्शक पदार्थाच्या कडेवरून किरणांचे, त्यांच्या छायेमध्ये वळणे) व ध्रुवण (प्रकाश तरंगांचे कंपन एकाच किंवा दोन विशिष्ट प्रतलांत म्हणजे पातळ्यांत मर्यादित होणे) प्रकाशाप्रमाणेच होते. प्रकाशाप्रमाणेच त्यांना माध्यमाची जरूरी भासत नाही व त्यांची तीव्रताही प्रकाशाप्रमाणेच अंतराच्या वर्गाच्या व्यस्त प्रमाणात बदलते.

कोणताही पदार्थ तापविला असता त्यापासून उष्णता तरंग बाहेर पडतात. पदार्थाचे तापमान जसजसे वाढवावे तसतशी तरंगलांबी कमी कमी होत जाते. शेवटी दृश्य प्रकाश व नंतर जंबुपार किरण उद्‍भवतात. एका साध्या प्रयोगाने हे सिद्ध करता येईल. काजळीने माखलेल्या एका प्लॅटिनमाच्या तारेतून जर विद्युत् प्रवाह सोडला व तो वाढवत नेला, तर प्रथम उष्णता प्रारण बाहेर पडते. तारेजवळ विद्युत् प्रवाहमापक जोडलेल्या तपयुग्माचे (तांबे व लोखंड यांसारख्या दोन निरनिराळ्या विद्युत् संवाहकांची टोके एकत्र जोडून व उरलेली टोके विद्युत् प्रवाहमापकास जोडून तयार होणार्‍या आणि एकत्र जोडलेल्या टोकांचे तापमान मोजणार्‍या साधनाचे) एक टोक जर नेले तर विद्युत प्रवाहमापक तापविद्युत् (तपयुग्मासारख्या साधनाच्या दोन टोकांतील तापमान फरकामुळे निर्माण होणारा विद्युत् प्रवाह) दर्शवितो. यावरून प्रारणाच्या रूपाने ऊर्जा बाहेर पडते, हे सिद्ध होते. पुढे तारेतील विद्युत् प्रवाह जसजसा वाढवावा तसतसे प्रथम तार किंचित तांबडी (५२५^० से. ) तांबडी (९००^० से.), नारिंगी (१,१००^० से.), पिवळी (१,२५०^० से.) व शेवटी पांढरी (१,६००^० से.) दिसू लागेल.

सूर्याचे तापमान अत्युच्च असल्याने त्यापासून उष्णता प्रारण व प्रकाश यांची निर्मिती होते. यापैकी बरीचशी उष्णता वातावरणात शोषली जाते. शिवाय पृथ्वीचे सूर्यापासूनचे अंतर बरेच असल्याने,फार मोठ्या क्षेत्रफळावर उष्णता पसरते व त्यामुळे तिची तीव्रता कमी होते.

उष्णता प्रारण जेव्हा एखाद्या पदार्थावर पडते तेव्हा त्यातील काही भागाचे परावर्तन होते, काही भागाचे शोषण होते व उरलेल्या भागाचे प्रेषण (बाहेर टाकण्याचे कार्य) होते. जर एकंदर प्रारण ऊर्जेपैकी परावर्तित अंश r शोषित अंश a व प्रेषित अंश t असेल तर r + a = t = 1 हे समीकरण मिळते. r, a, आणि t यांची मूल्ये तरंगलांबी λ वर अवलंबून असतात. म्हणून तरंगलांबी λ असताना rλ स परावर्तनाचा गुणांक aλ स शोषणाचा गुणांक व tλ स प्रेषणाचा गुणांक असे संबोधतात.

उत्सर्जक शक्ती (eλ) : ठराविक तापमानास पदार्थाच्या एकक क्षेत्रफळापासून दर सेकंदाला λ व λ+ dλ या छोट्या टप्प्यातील तरंगलांबीतील उत्सर्जित होणारी ऊर्जा e_λdλ इतकी असते, यातील e_λया राशीस त्या पदार्थाची त्या तापमानाची उत्सर्जक शक्ती म्हणतात.

प्रीव्होस्ट यांचा उष्णता विनिमय सिद्धांत : या सिद्धांताप्रमाणे निरपेक्ष शून्याहून [- २७३^० सें हून, → केल्व्हिन निरपेक्ष तापक्रम] अधिक तापमान असलेला कोणताही पदार्थ उष्णतेचे उत्सर्जन करतो, पदार्थाच्या तापमानातील वाढीबरोबर त्यापासून होणारे उष्णतेचे उत्सर्जनही वाढते. सभोवतालच्या पदार्थाशी कमीअधिक प्रमाणात होणार्‍या उष्णतेच्या देवाणघेवाणीमुळे पदार्थाचे तापमान बदलते. यामुळे दोन भिन्न तापमानांचे पदार्थ एकमेकांशेजारी ठेवले असता थोड्याच वेळात त्यांचे तापमान एकमेकांबरोबर होते. परंतु जरी दोघांचे तापमान सारखे झाले, तरी त्यांची उष्णतेची देवाणघेवाण चालूच राहते. म्हणजे तापमान एक झाले याचा अर्थ ते पदार्थ समतोलित अवस्थेत आहेत. ‘प्रत्येक पदार्थ (समतोलित स्थितीत असताना) विशिष्ट कालांतरात जेवढी उष्णता आत घेतो तेवढीच उष्णता त्याच कालांतरात बाहेर टाकतो’, यालाच प्रीव्होस्ट यांचा उष्णता विनियम सिद्धांत म्हणतात.

कृष्ण पदार्थ : एखादा पदार्थावर पडलेल्या उष्णतेचे, जर त्या पदार्थामुळे परावर्तन अथवा प्रेषण मुळीच होत नसेल व फक्त शोषणच होत असेल, तर अशा पूर्णशोषक पदार्थाला ‘कृष्ण पदार्थ’ असे म्हणतात. असा कृष्ण पदार्थ प्रत्यक्षात अस्तित्वात नाही परंतु जवळजवळ पूर्णशोषक असे पदार्थ आहेत. उदा., दिव्याची काजळी, प्लॅटिनमाची काजळी वगैरे. हे पदार्थ ९६ ते ९८ टक्के उष्णतेचे शोषण करतात .कृष्ण पदार्थ जसा उष्णतेचा उत्तम शोषक असतो, तसाच तो उत्तम उत्सर्जकही असतो.

स्थिर तापमान असलेल्या बंद भांड्यातील प्रारण कृष्ण पदार्थाच्या प्रारणासारखेच असते. अशा भांड्यास एक लहान छिद्र ठेवले, तर त्या छिद्रातून आत जाणारे प्रारण आतल्या आत अनेक वेळा परावर्तित झाल्याने त्या प्रारणाचे संपूर्ण शोषण होते; तसेच त्या छिद्रातून बाहेर पडणारे प्रारणही त्या तापमानाला होऊ शकणारे संपूर्ण प्रारण असते.

वीन व लुमर यांनी आतून काळे केलेले पितळेचे अथवा प्लॅटिनमाचे नळकांडे कृष्ण पदार्थ म्हणून वापरले. नळकांड्याचे तापमान विद्युत् प्रवाहाने स्थिर राखले होते. नळकांड्याच्या टोकाला ठेवलेल्या एका सूक्ष्म छिद्रातून प्रारण बाहेर पडले. नळकांडे चिनी मातीच्या नळ्यांनी वेष्टिलेले होते.

फेरी यांनी आ. १ मध्ये दाखविल्याप्रमाणे कृष्ण पदार्थ बनविला. त्यात अ हे छिद्र असून छिद्रासमोरचा भाग आ त्यापासून फारसे उत्सर्जन होऊ नये म्हणून शंकूच्या आकाराचा बनविला. या पूर्ण शोषकांचे वैशिष्ट्य असे की, त्यामध्ये कोणताही पदार्थ ठेवला असता, त्यापासून उद्‌भवणारे प्रारण कृष्ण पदार्थाच्या प्रारणाप्रमाणेच असते.

 किरखोफ यांचा नियम : कोणत्याही लांबीच्या उष्णता तरंगांना प्रतिबंध करणारे एक बंदिस्त कोटर आहे. व कोटराच्या भिंतींचे तापमान एकसारखे आहे अशी कल्पना करा. अशा कोटरामध्ये जर एखादा पदार्थ ठेवला, तर तो पदार्थ व बंदिस्त कोटराच्या भिंती या दरम्यान उष्णतेची देवाण-घेवाण सुरू होऊन शेवटी दोघांचेही तापमान सारखे होईल. आता फक्त λ व λ + dλ या मर्यादेतील लांबीचे तरंग विचारात घेऊ. समजा, पदार्थाची शोषक शक्ती aλ आहे, उत्सर्जक शक्ती eλ आहे, तापमान T आहे व दर सेकंदाला पदार्थाच्या एकक पृष्ठभागावर पडणारी उष्णता ऊर्जा dQ आहे. मग, दर सेकंदाला पदार्थाचा एकक पृष्ठभाग aλdQ इतकी उष्णता शोषतो व उरलेली ऊर्जा (1-a_λ) dQ परावर्तित किंवा प्रेषित होते. शिवाय दर सेकंदाला पदार्थाचा एकक पृष्ठभाग e_λdλ इतकी उष्णता उत्सर्जित करतो. समतोल अवस्थेत पदार्थाला मिळणारी व पदार्थामधून बाहेर जाणारी दर सेकंदातीला ऊर्जा सारखीच असली पाहिजे. म्हणून

aλdQ = e_λdλ      …        …       …        (१)

असे समीकरण मिळते. कृष्ण पदार्थाच्या बाबतीत a_λ = 1 व e_λ चे मूल्य कमाल (म्हणजे E_λ) होते म्हणून कृष्ण पदार्थ वा पूर्ण शोषकाच्या बाबतीत

dQ = E_λdλ       …        …        …          (२)

हे समीकरण मिळते. समी. (१) व (२) यांची तुलना केली असता

eλ/aλ = Eλ        …        …        …          (३)

हे समीकरण मिळेत. हे समीकरण म्हणजेच किरखोफ सिद्धांत होय. तो पुढीलप्रमाणे सांगता येईल : ‘कोणत्याही ठराविक तापमानास पदार्थाची उत्सर्जक शक्ती व शोषक शक्ती यांचे गुणोत्तर अचल राहते व ते त्याच तापमानाच्या कृष्ण पदार्थाच्या उत्सर्जन शक्तीएवढे असते’. किरखोफ यांचा नियम फ्ल्यूगर यांनी प्रयोगाने सिद्ध केला. प्रयोगामध्ये त्यांनी तोरमल्ली (टुर्मलीन) स्फटिकामुळे होणारे उत्सर्जन व शोषण मोजले. किरखोफ यांच्या सिद्धांताने खगोलीय भौतिक व वर्णपटविज्ञान या विज्ञान शाखांचा उदय झाला.

सूर्याच्या वर्णपटामध्ये आढळणार्‍या फ्राइनहोफर रेषांचे (फ्राउनहोफर या जर्मन शास्त्रज्ञांनी शोधून काढलेल्या व त्यांच्या नावाने ओळखल्या जाणार्‍या रेषांचे) स्पष्टीकरण या सिद्धांतामुळे शक्य झाले. सूर्याच्या मध्यभागाचे तापमान त्याच्या भोवतीच्या वातावरणापेक्षा पुष्कळच जास्त आहे. सूर्यकिरणांपासून मिळणारा वर्णपट मुळात अखंड असतो. परंतु हे सूर्यकिरण जेव्हा सूर्याच्या वातावरणातून जातात, तेव्हा त्यातील सोडियम, तांबे वगैरे वायुरूपातील पदार्थ ठराविक तरंगलांबीचे किरण शोषतात यामुळे वर्णपटदशर्कात दिसणार्‍या सूर्याच्या वर्णपटात त्या त्या जागी काळ्या रेषा दिसतात. हेच पदार्थ तापविले असता त्यांच्यापासून त्याच तरंगलांबीचे किरण उत्सर्जित होतात. उदा., सोडियम धातू पिवळे किरण शोषतो व तो तापविला असता पिवळेच किरण उत्सर्जित करतो. यावरून किरखोफ यांच्या सिद्धांताचा अचूकपणा, सिद्ध होतो. यंग यांनी १८७२ मध्ये संपूर्ण सूर्यग्रहणाच्या वेळी सूर्याचा वर्णपट अभ्यासिला. त्यावेळी सूर्याच्या वातावरणातील पदार्थ चमकू लागून त्यांचा वर्णपट मिळाला. या वर्णपटातील रेषा एरव्ही दिसणार्‍या फ्राउनहोफर रेषांच्या जागीच आहे. असे त्यांना दिसून आले.

किरखोफ यांच्या शोधामुळे योग्य प्रकारे उत्तेजित झालेल्या निरनिराळ्या प्रत्येक अणूपासून ठराविक तरंगलांबीचाच प्रकाश उत्सर्जित होतो व ही तरंगलांबी त्या अणूची गुणदर्शक असते, हे प्रथमच सिद्ध झाले. फ्राउनहोफर रेषांच्या अभ्यासावरून कित्येक मूलद्रव्यांचा शोध लागला [→ वर्णपटविज्ञान] .

करड्या पदार्थाचे प्रारण : कृष्ण पदार्थापासून उत्सर्जित होणार्‍या प्रारण ऊर्जेचा तिच्या वितरणाप्रमाणे वर्णपट मिळतो. ऊर्जेचे हे वितरण संपूर्ण वर्णपटात (किंवा एका ठराविक टप्प्यातील तरंगलांबीमध्ये) जर एका स्थिर गुणकाने कमी केले, तर करड्या पदार्थाला लागू पडणारे ऊर्जा वितरण मिळते. यावरून असे दिसून येईल की, करड्या वर्णाच्या पदार्थापासून उत्सर्जित होणार्‍या प्रारण ऊर्जेचे वितरण कृष्ण पदार्थापासून उत्सर्जित होणार्‍या प्रारण ऊर्जेच्या वितरणासारखेच पण एका स्थिर गुणकाने कमी केलेले, असे असते. उदा., वर्णपटाच्या दृश्य भागात बहुतेक धातूंची उत्सर्जक शक्ती समान असते म्हणून या धातू दृश्य वर्णपटात करड्या पदार्थाप्रमाणेच वागतात. करड्या वर्णाची कल्पना काही पदार्थापासून उद्‍भवणार्‍या प्रारणांची तीव्रता आजमाविण्यासाठी उपयोगी पडते. याकरिता श्टेफान-बोल्टसमान सिद्धांत उपयोगी पडतो. (या सिद्धांतासंबंधीचे विवरण खाली आले आहे.).

प्रारणाचा दाब : उष्णता प्रारणाचे गुणधर्म प्रकाशाप्रमाणेच असल्यामुळे प्रकाशाप्रमाणेच त्यांचाही थोडा पण निश्चित दाब पडतो. केल्पर यांना या दाबाची अंधुक कल्पना, सूर्याकडे जाणार्‍या धूमकेतूची शेपटी त्याच्या विरुद्ध दिशेस नेहमी राहते या निरीक्षणावरून फार पूर्वीच आली होती. परंतु प्रारणाच्या दाबाच्या कल्पनेला त्यावेळी प्रायोगिक पुरावा मिळू न शकल्याने ती कल्पना तेव्हा सोडून द्यावी लागली. परंतु पुढे १८७० मध्ये मॅक्सवेल यांनी प्रकाशाचा विद्युत् चुंबकीय सिद्धांत मांडला व त्यामध्ये प्रकाशाला थोडा दाब असतो आणि हा दाब समांतर प्रकाशशलाकांच्या बाबतीत प्रकाशाच्या ऊर्जेच्या घनतेएवढा असतो, असे त्यांनी दाखविले (आ.२) जर प्रारणाची तीव्रता I असेल (दर सेकंदाला एकक पृष्ठभागावर लंब दिशेने पडणारी ऊर्जा), प्रकाशाचा वेग c असेल व प्रारणाची ऊर्जा घनता ε असेल, तर समांतर प्रारणाचा दाब

P = ε = I/c        …        …        …          (४)

इतका असतो. जर प्रारण समांतर नसून सर्व बाजूंस सारखे विखुरलेले असेल, तर दाबाची तिन्ही अक्षांच्या दिशांना समान वाटणी होते. म्हणून

P = ε/3              …        …        …          (५)

असे समीकरण मिळते. बार्टोली यांनी उष्मागतिकीच्या दुसर्‍या सिद्धांताच्या साहाय्याने [→उष्मागतिकी ] प्रारणास दाब असतो, असे सिद्ध केले.

श्टेफान–बोल्टस्‌मान यांचा सिद्धांत : टिंड्‍ल आणि डुलाँग व पेटिट यांच्या प्रयोगांच्या आधारे १८७९ मध्ये श्टेफान यांनी असा नियम मांडला की, ‘कोणत्याही पदार्थापासून प्रति-सेंकंदाला व प्रतिसेंमी.² क्षेत्रफळाकडून उत्सर्जित होणारी प्रारण ऊर्जा ही त्या पदार्थाच्या निरपेक्ष तापमानाच्या चतुर्थ घाताच्या सम प्रमाणात असते’. १८८४ मध्ये बोल्टस्‌मान यांनी हा नियम ऊष्मागतिकीच्या साहाय्याने सिद्ध केला व असे दाखविले की, हा नियम कृष्ण पदार्थाना पूर्णांशाने लागू पडतो. म्हणून हा नियम ‘श्टेफान –बोल्टसमान सिद्धांत’ म्हणून ओळखला जातो. हा सिद्धांत असा जर T₀ ⁰ के. (निरपेक्ष) तापमानाचा एक कृष्ण पदार्थ T⁰ के. तापमानाच्या दुसर्‍या कृष्ण पदार्थाने वेढलेला असेल तर प्रति-सेंकंदाला पहिल्या पदार्थाच्या प्रत्येक सेंमी.^२ पृष्ठभागापासून बाहेर पडणारी ऊर्जा E ही (T⁴ – T0⁴) या प्रमाणात असते म्हणून

E = o (T⁴ –T₀⁴)          …        …        …          (६)

यात ० हा श्टेफान स्थिरांक आहे. त्याचे मूल्य ५·७ × १०^-५ अर्ग से. ^-१ (सेंमी)^-२ (^०के) ^-४ इतके आहे. लुमर आणि प्रिंगशाइम यांनी हा सिद्धांत १००^० से. ते १,२६०^० से. या तापमानाच्या मर्यादेत पडताळून पाहिला. त्यांची प्रयोग रचना आ.३ मध्ये दाखविली आहे. आ हा लुमर-कुर्लबॉम उष्णतामापक असून उष्णतामापक असून अ या भांड्यातील उकळते पाणी प्रमाण प्रारणांचे उगमस्थान आहे व त्याचा उपयोग उष्णतामापकाचे अंशक परिक्षण करण्यासाठी (मापप्रमाण निश्चित करण्यासाठी) होतो. इ हा कृष्ण पदार्थ उत्सर्जक असून त्याचे तापमान ई या तपयुग्माच्या मदतीने मोजता येते.

प्रयोग जर २००^० से. ते ६००^० से. या टप्प्यात करावयाचा असेल, तर आतून प्लॅटिनमाची काजळी माखलेला एक तांब्याचा पोकळ गोल कृष्ण पदार्थ म्हणून वापरतात. गोल तापविण्यासाठी सोडियम व पोटॅशियम नायट्रेट यांचे मिश्रण असलेल्या एका कुडांत तो ठेवतात. हे मिश्रण २१९^० से. तापमानास वितळते. प्रयोग जर ९००^० से. ते १,२००^० से. या टप्प्यात करावयाचा असेल तर आतून प्लॅटिनमाची काजळी माखलेल्या लोखंडी भांड्याची कृष्ण पदार्थ म्हणून योजना करतात व ते भांडे दुहेरी भिंतीच्या वायुभट्टीच्या साहाय्याने तापवितात. तपयुग्म तापमापक एका चिनी मातीच्या नळकांड्यात ठेवलेले असते. उ हे जरूर तेव्हा वापरावयाचे पडदे पाण्याने थंड केलेले असतात व ते प्रारणास उष्णतामापकाकडे जाण्यास प्रतिबंध करू शकतात.

कृष्ण पदार्थाच्या वर्णपटातील प्रारण ऊर्जेचे वितरण : पदार्थापासून उत्सर्जित होणार्‍या प्रारणाची तरंगलांबी एकच नसून तरंगलांबींचा एक अखंड वर्णपटच असतो. या वर्णपटातील ऊर्जेचे वितरण कसे होते हे समजणे आवश्यक आहे. याकरिता वीन, रॅली व जीन्स यांनी ऊष्मागतिकी व विद्युत्‌ चुंबकीय सिद्धांत यांचा उपयोग करून काही नियम सिद्ध केले. त्यांची पद्धत क्लिष्ट असून नियम तितकेसे परिपूर्ण नाहीत. परंतु त्याच्या या कामगिरीमुळेच पुढे प्लांक (९१०१) यांना त्यांच्या पुंज कल्पनेवर आधारलेला नवीन परिपूर्ण असा नियम मांडता आला.

वीन यांचा सिद्धांत : वीन यांनी १८९३ मध्ये असे सिद्ध केले की, कृष्ण पदार्थाच्या दर सेंमी.^२ पृष्ठभागापासून प्रति-सेकंदाला उत्सर्जित होणार्‍या λ आणि λ + dλ या तरंगलांबींच्या मर्यादेतील प्रारण ऊर्जा

E_λdλ = A/λ⁵F (λT) dλ          …        …        (७)

असते. समीकरण (७) यास वीन यांचा ऊर्जा वितरणाचा सिद्धांत म्हणतात. यात T हे कृष्ण पदार्थाचे निरपेक्ष तापमान असून f (λ T) हे λT चे अज्ञात फलन (गणितीय संबंध) आहे व A हा स्थिरांक आहे.

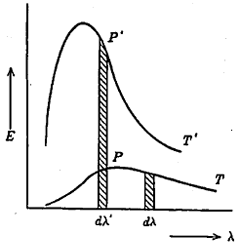
ऊर्जा वितरण जर कोणत्याही एका तापमानास (T) माहीत असेल तर ते कोणत्याही दुसर्‍या तापमानास (T’) आ. ४ मध्ये दाखविल्याप्रमाणे काढता येईल त्यासाठी भुज (आडवा अक्ष) T/T या प्रमाणात कमी केला पाहिजे व कोटी (उभा अक्ष) (T/T’)⁵ या प्रमाणात वाढविली पाहिजे. यामुळे आलेखाची उंची वाढेल, पण तो आकुंचित होईल .आलेखांतर्गत क्षेत्रफळ (म्हणजेच एकूण ऊर्जा तीव्रता) (T / T)⁴ या प्रमाणात बदलेल. यावरून श्टेफान यांच्या नियमाला पुष्टी मिळते. T’ तापमानाच्या आलेखात कमाल उत्सर्जन बिंदू P’ आहे (आ. ४), तर T तापमानाच्या आलेखात P आहे. या कमाल बिंदूस अनुलक्षून तरंगलांबी अनुक्रमे λm व λm असल्यास,

λmT = λm’T’= स्थिरांक        …        …        …          (८)

याचा अर्थ असा की, तापमान वाढल्यास आलेखाच्या परमोच्च बिंदूस अनुलक्षून असलेली तरंगलांबी λm कमी होते यास वीन यांचा ‘स्थलांतर नियम’ म्हणतात.

वीन यांच्या सिद्धांताचा प्रायोगिक पडताळा : वीन यांच्या सिद्धांताची प्रायोगिक परीक्षा पाशेन, लुमर आणि प्रिंगशाइम, रूबेन्स आणि कुर्लबॉम वगैरे शास्त्रज्ञांनी केली. लुमर आणि प्रिंगशाइम यांच्या प्रयोगात त्यांनी ६२१^० के. ते १,६४६^० के. तापमानांच्या पट्ट्यात ऊर्जा वितरण मोजले व आलेख  काढले (आ.५) आणि ते वीन समीकरणावरून (समी. ७) काढलेल्या आलेखाबरोबर ताडून पाहिले.

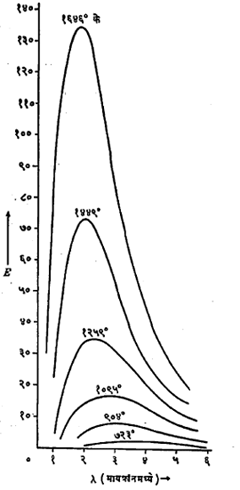
या तुलनेमध्ये λmT = स्थिरांक हा वीन यांचा स्थलांतर नियम बरोबर असल्याचे दिसून आले. परंतु वीन यांचा ऊर्जा वितरणाचा सिद्धांत

फक्त लहान तरंगलांबींच्याच प्रारणांना लागू पडतो, असे दिसून आले.

सैद्धांतिक आलेख काढण्यासाठी वीन यांच्या सिद्धांतातील f या अज्ञात फलनाचे मूल्य माहीत असणे जरूर आहे. हे मूल्य वीन यांनी काही अनुमाने ठरवून त्यावरून काढले.

रॅली-जीन्स यांचा सिद्धांत : त्यानंतर रॅली व जीन्स यांनी मॅक्सवेल यांच्या विद्युत् चुंबकीय सिद्धांताचा आधार घेऊन नवीन सिद्धांत प्रस्थापित केला. प्रथमतः कंपनाच्या किती तर्‍हा आहेत, याचा विचार करू.

समजा p, q व r लांबीच्या बाजू असलेली स्थितिस्थापक (विकृती घडवून आणणार्‍या प्रेरणा काढून घेतल्यावर मूळ स्थितीस परत येणार्‍या) पदार्थापासून बनविलेली एक काटकोन चौकोनकृती पेटी आहे व या पेटीत सर्व दिशांना असणारी स्थिर कंपने निर्माण झालेली आहेत. कोणत्याही एका तरंगाच्या सुरुवातीच्या दिक्‌कोज्या (एखाद्या रेषेने सहनिर्देशक अक्षांशी केलेल्या कोनांची कोज्या गुणोत्तरे) जर 1, m व n असतील, तर पेटीच्या भिंतीपासून जेव्हा त्या तरंगाचे परावर्तन होते, तेव्हा त्याच्या दिक्‌कोज्या +1, m ,+n या आठांपैकी कोणत्याही असू शकतील. म्हणजेच परावर्तनाची दिशा या आठांपैकी कोणतीही एक असू शकेल. तरंग स्थिर असल्यामुळे एका परावर्तनानंतर N λ/2 एवढे अंतर चालून गेल्यानंतरच त्याचे दुसरे परावर्तन होऊ शकेल येथे N हा कोणताही पूर्णांक आहे व λ तरंगलांबी आहे. म्हणून

 यात n₁, n₂, n₃ हे अर्थातच पूर्णोक आहेत. पण 1² + m² + n² = 1 असल्याने,

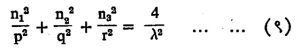हे समीकरण मिळते. याचा अर्थ असा आहे की, ज्या कंपनांची तरंगलांबी समी. (९) ची पूर्तता करील त्याच कंपन पद्धती शक्य असतील.

एकमेकांशी काटकोन करणारे ती अक्ष घेऊन व n₁, n₂, n₃ यांस पूर्णांक मूल्ये देऊन जर आलेख काढला, तर अनेक बिंदूची एक जाळी तयार होते. यातील प्रत्येक बिंदू, ठराविक दिशेने जाणारे व ठराविक तरंगलांबीचे एक स्थिर कंपन दर्शवितो. समी (९) हे लंबगोलाचे समीकरण आहे. यातील प्रत्येक एकक घनफळात एक बिंदू येतो. म्हणजेच त्याच्या घनफळाइतकी स्थिर कंपने शक्य आहेत.

आता λ व λ+dλ या टप्प्यातील तरंगलांबीच्या कंपनांचा जर विचार केला, तर या कंपनांची संख्या दोन लंबगोलांमधील पोकळीच्या घनफळाएवढी असणार, हे उघड आहे. लंबगोलाचे घनफळ असल्याने पोकळीचे घनफळ

प्रत्येक कंपन आठ प्रकारे होऊ शकत असल्याने प्रत्यक्ष कंपनांची संख्या 

इतकी येते (v = pqr = पेटीचे घनफळ). म्हणून प्रत्येक एकक घनफळातील λ व λ + dλ या टप्प्यातील तरंगलांबींच्या कंपनांची संख्या =4ndλ/λ⁴.विद्युत् चुंबकीय तरंगात,विद्युत् व चुंबकीय अशा दोन वेगवेगळ्या प्रकारांचे एकमेकांशी काटकोन करणारे तरंग असल्याने व प्रत्येक प्रकारच्या एकक घनफळातील कंपनांची संख्या 4ndλ/λ⁴ असल्याने एकक घनफळातील एकूण कंपने 8ndλ/ λ⁴इतकी होतील.

ऊर्जेच्या समवितरणाच्या रूढ तत्त्वानुसार प्रत्येक मुक्तमात्रेशी (एखाद्या प्रणालीची स्थिती निश्चित करणार्‍या बदलत्या राशींच्या म्हणजे चलांच्या संख्येत मुक्तमात्रा म्हणतात) 1/2 KT इतकी गतिज ऊर्जा व तितकीच स्थितिज ऊर्जा निगडीत असल्याने,प्रत्येक मुक्तमात्रेशी निगडीत असलेली एकूण ऊर्जा kT असते, म्हणूनλव λ +dλ या टप्प्यातील एकक घनफळातील ऊर्जा, म्हणजेच ऊर्जा घनता

इतकी असते. येथे k हा बोल्टसमान स्थिरांक आहे. हे समी. (१०) म्हणजेच रॅली-जीन्स यांचा प्रारणाचा ‘ऊर्जा वितरणाचा सिद्धांत’ होय. हे समीकरण प्रायोगिक आलेखाशी ताडून पाहिले असता असे दिसून आले की, ते फक्त मोठ्या तरंगलांबीच्या तरंगांनाच लागू पडते व लहान तरंगलांबींना ते लागू पडत नाही.

वीन आणि रॅली-जीन्स यांच्या सिद्धांतांतील विसंगतीचा विचार करता माक्स फ्लांक यांनी असे अनुमान काढले की, हे नियम सिद्ध करताना रूढ भौतिकीय तत्त्वांचा आधार घेतला गेला, हेच मुळात चुकले असावे. म्हणून त्यांनी १९०१ मध्ये अगदी नवीन व क्रांतिकारक असा स्वतःचा पुंज सिद्धांत मांडला. एका बंद भांड्यातील वायूच्या रेणूंस सांख्यिकीतील (संख्याशास्त्रातील) नियम लागू करून,

रेणूंच्या शक्य असलेल्या अनेक कंपनांत विभागलेल्या ऊर्जेपैकी E व E+dE या छोट्या टप्प्यातील ऊर्जा वितरणाची सर्वाधिक संभाव्यता Ae ^{– E/kT} इतकी येते, असे त्यांनी दाखविले. यात A हा कंपनांच्या संख्येवर अवलंबून असणारा स्थिरांक असून T हे निरपेक्ष तापमान व K हा बोल्टसमान स्थिरांक आहे. ऊर्जेच्या विभागणीत,रूढ भौतिकीनुसार ऊर्जा E ही 0 व ∞ या मर्यादेतील कोणतेही मूल्य घेत नसून ती E=0 , E= ε E = 2 ε अशी मूल्ये घेते, असे त्यांनी मानले. याचा अर्थ असा होतो की , 0 व E = ε E= 2ε … अशी मूल्ये घेते, असे त्यांनी एक शून्य तरी असू शकेल अथवा ε असू शकेल. या दोहोंच्या दरम्यानचे कोणतेही मूल्य E घेऊ शकणार नाही. या त्यांच्या गृहीता प्रमाणे ε हा ऊर्जेचा लहानात लहान पुंज (क्वांटम) असून E चे मूल्य E = n ε (n = 0, 1,2 …) असेच असू शकते. म्हणून त्यांनी मांडलेल्या या सिद्धांतास पुंज सिद्धांत असे नाव प्राप्त झाले.

आता dE हा वरील ऊर्जामूल्याभोवतीचा एक अती लहान व समान टप्पा आहे असे समजल्यास E = O , E = ε, E= 2 ε … ऊर्जामूल्यांच्या कंपनाची संख्या 1: e^{– ε/kt}:…या प्रमाणात असेल. यावरून एकूण कंपने

इतकी होतात. या सर्व कंपनांची एकूण ऊर्जा =

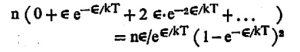इतकी येते. म्हणून एकूण ऊर्जेस एकूण कंपनांच्या संख्येने भागले असता कंपनाची सरासरी ऊर्जा

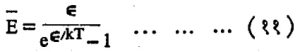 येते. समी. (११) प्रमाणे ε → 0 असताना, Ē = kT येते व ही गोष्ट रूढ भौतिकीच्या तत्त्वाशी जळणारी आहे.

प्लांक यांचा ऊर्जा वितरणाचा सिद्धांत : वर्णपटातील ऊर्जा वितरणाची समस्या सोडविण्याच्या बाबतीत रूढ यामिकी अयशस्वी ठरली, हे मागे नमूद केले आहेच. प्लांक यांचा पुंज सिद्धांत या दृष्टीने यशस्वी ठरला आहे. विज्ञानातील इतर शाखांमध्येही या सिद्धांताचा यशस्वीरीत्या अवलंब केला गेला आहे व ही गोष्ट या सिद्धांताची सत्यता दर्शविते.

पुंज सिद्धांताचे नियम : (१) ν कंप्रता असलेल्या कंपित्राची (कंपने करणार्‍या साधनाची) ऊर्जा nhv इतकी असते. येथे h हा विश्वस्थिरांक असून त्यास प्लांक स्थिरांक म्हणतात. (२) शून्य निरपेक्ष तापमानातही कंपित्राची ऊर्जा शून्य होत नसून ती प्रत्येकी 1/2hv इतकी असते. म्हणून v कंप्रता असलेल्या एका कंपित्राची ऊर्जा E = (n+ ½) hv अशी येते (यात n चे मूल्य ०,१,२,३,.. या पूर्णांकांपैकी कोणतेही असू शकते). n ची मूल्ये एकामागून एक वरील सूत्रात वापरता E =1/2hv, 2/3hv, 5/2hv,… अशी ऊर्जामूल्ये मिळतात (रूढ यामिकीशी हे विसंगत आहे, कारण त्याप्रमाणे ऊर्जामूल्य 0 पासून ∞ पर्यंत कोणतेही असू शकते). याचा अर्थ असा आहे की, प्रारण ऊर्जेचे उत्सर्जन किंवा शोषण पुंजाने होते.म्हणून कंप्रता असलेल्या व λ तरंगलांबी असलेल्या (v= c/λ , c = प्रकाशवेग) कंपित्राची सरासरी ऊर्जा

 

इतकी येते. मागे सिद्ध केल्याप्रमाणेλ व λ +dλ या टप्प्यातील एकक घनफळातील तरंगलांबीची संख्या 8/λ⁴ dλ असल्याने , वर्णपटातील ऊर्जा वितरण पुढीलप्रमाणे होते :

 

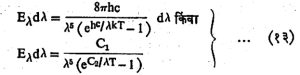
येथे C1 = 8πhc व C2 = hc/k स्थिरांक आहेत. समी. (१३) प्लांक यांचा ऊर्जा वितरणाचा सिद्धांत म्हणून ओळखले जाते. जेव्हा लहान λ असेल,तेव्हा हे समीकरण वीन समीकरणाचे [समी. (७) चे] रूप धारण करते. तसेच जेव्हा तरंगलांबी λ मोठी असेल, तेव्हा हे समीकरण रॅली-जीन्स समीकरणाचे [समी. (१०) चे] रूप धारण करते.

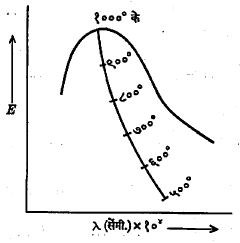
१,०००^० के. तापमानाच्या कृष्ण पदार्थाच्या वर्णपटातील ऊर्जा वितरणाचा प्लांक यांच्या समीकरणावरून काढलेला आलेख आ. (६) मध्ये दाखविला आहे. त्यातील तुटक रेषा ही निरनिराळ्या तापमानाच्या आलेखांच्या महत्तम बिंदू मधून काढलेली आहे. लुमर व प्रिंगशाइम, पाशेन वगैरे शास्त्रज्ञांनी काढलेल्या प्रायोगिक आलेखाशी हा आलेख पूर्णांशाने जुळतो. समी (१३) चे λ स अनुलक्षून अवकलन [→ अवकलन व समाकलन] करून येणारे पद शून्याबरोबर मांडून, महत्तम बिंदूस अनुलक्षून असलेले λm चे मूल्य मिळते. ते असे

४·९६५१ = C₂/ λ_mT     …        …       …            (१४)

C२ चे प्रायोगिक मूल्य १·४३८७९ (सेंमी.) (^०के.) असल्याने समी. (१४) वरून m चे मूल्य काढणे शक्य होते. λm कळल्यामुळे, λm T = स्थिरांक हा वीन यांचा स्थलांतर नियम पडताळून पाहता येतो. या स्थिरांकाचे मूल्य ०·२८९७ (सेंमी.) (^०के.) येते.

संपूर्ण प्रारणाची एकूण ऊर्जा घनता समी. (१३) ने λ च्या O पासून ∞पर्यंतच्या मर्यादांत समाकलन करून मिळते.

 

(से.)^-१ (^०के)^-४ इतके आहे. σ व C₂ यांची प्रायोगिक मूल्ये समी. (१६) मध्ये व C₂ = hc/k या समीकरणात वापरल्या असता प्लांक यांचा विश्वस्थिरांक

h = (६·६२५६ ± -०·००००२४) × १०^-२७ अर्ग सेकंद व बोल्टसमान यांचा विश्वस्थिरांक

k = (१·३८०५४ ± ०·००००४७) × १०^-१६ अर्ग (^०के)^-१ ही महत्त्वाची मूल्ये मिळतात. K च्या ज्ञात मूल्यावरून ॲव्होगाड्रो स्थिरांक N (एका ग्रॅम-रेणूमधील म्हणजे ग्रॅममध्ये मोजलेल्या रेणुभाराइतक्या पदार्थातील रेणूंची संख्या) चे मूल्य मिळते.

N= (६·०२२५२ ± ०·००११) ×१०^२३ (मोल)^-१

प्रारणाचे शोषण : प्रारण जेव्हा घन, द्रव अथवा वायुरूप पदार्थातून जाते तेव्हा त्याची तीव्रता कमी होते. याचे एक कारण म्हणजे ध्यमात होणारे प्रारणाचे शोषण होय. याशिवाय प्रारणाच्या प्रकीर्णनामुळे (विखुरण्यामुळे) सुद्धा त्याची तीव्रता कमी होते.

जेव्हा पदार्थावर पडणार्‍या सर्व तरंगांचे सारख्या प्रमाणात शोषण होते तेव्हा त्या शोषणास ‘सर्वसाधारण’ शोषण म्हणतात. यामुळे अशा पदार्थांमधून बाहेर पडणार्‍या प्रारणाची (प्रकाशाची) तीव्रता कमी होते व ते पदार्थ करडे दिसतात. अशा तर्‍हेने सर्वच तरंगांचे सारख्या प्रमाणात शोषण करणारे पदार्थ नाहीत. परंतु अर्धपारदर्शक असा प्लॅटिनमाचा पातळ पडदा किंवा तत्सम पदार्थ हे जवळजवळ करडे म्हणण्यास हरकत नाही. याउलट बहुतेक पदार्थ तरंगांचे विवेचनात्मक (निवडक) शोषण करतात व यामुळेच पदार्थांना रंग प्राप्त होतो. उदा. हिरवी काच वर्णपटातील तांबड्या व निळ्या रंगाचे शोषण करते व म्हणून ती हिरवी दिसते.

पदार्थ कोणत्या तरंगांचे शोषण करतो ते पाहण्यासाठी वर्णपटदर्शक वापरतात. प्रकाशाचे उगमस्थान व वर्णपटदर्शक यांमध्ये पदार्थ ठेवून, पदार्थातून बाहेर येणार्‍या प्रकाशाच्या वर्णपटावरून त्या पदार्थाची शोषकता अजमावता येते. उष्णता प्रारणाच्या अभ्यासासाठी भिंगाऐवजी धातूचे अंतर्गोल परावर्तक वापरतात. याशिवाय उष्णता प्रारणाच्या मोजमापासाठी लँग्‍ली यांचा बोलोमीटर, तपचिती यांसारखी उपकरणे वापरतात.

घन अथवा द्रव पदार्थ बहुधा अखंड शोषणपट्टे दर्शवितात. काही धातूंचे शोषणपट्टे अतिशय अरुंद असतात व फार कमी तापमानास ते जवळजवळ काळ्या रेषांच्या रूपात दिसतात.

संपूर्ण वर्णपटाचा अभ्यास केला असता असे दिसून येईल की असा एकही पदार्थ नाही की, जो कोणत्या ना कोणत्या तरी तरंगाचे शोषण करीत नाही. धातू ज्या किरणांचे शोषण करतात ते सहसा त्यांच्या तरंगलांबीवर अवलंबून असत नाही. पण याला अपवाद आहेतच उदा., चांदीची पातळ पट्टी दृश्य प्रकाशाचे शोषण करते, परंतु ३,१६०^० अँगस्ट्रॉम (१ अँगस्ट्रॉम = १०^-८ सेंमी.) तरंगलांबीच्या व त्याच्या आसपासच्या जंबुपार किरणांना ती जवळजवळ पारदर्शक असते. विद्युत्‌ निरोधक (विद्युत् प्रवाहाला अतिशय रोध करणार्‍या) पदार्थाच्या बाबतीत सामान्यपणे तीन मोठे संक्रमण पट्टे असतात. एक पट्टा अतिलघुतरंगांच्या भागात, दुसरा मध्यम (दृश्य प्रकाशाच्या) तरंगलांबींच्या भागात व तिसरा दीर्घ तरंगांच्या भागात असतो. हे पट्टे पदार्थाप्रमाणे बदलतात. उदा. पाणी दृश्य प्रकाशाला पारदर्शक व अवरक्त किरणांना अपारदर्शक आहे, तर रबर दृश्य किरणांना अपारदर्शक व अवरक्त किरणांना पारदर्शक आहे. वायुरूप पदार्थाच्या शोषण वर्णपटात बहुधा अरुंद अशा काळ्या रेषा आढळतात. वायू जर हीलियम किंवा पार्‍याची वाफ यासारख्या एक-आणवीय (ज्याच्या रेणूत एकच अणू आहे असा) असेल, तर या रेषा खर्‍या अर्थाने रेषा असतात व त्या रेखीव असतात. शोषण वर्णपटातील रेषांची संख्या उत्सर्जन वर्णपटातील रेषांपेक्षा कमी असते. त्यामुळे शोषण वर्णपट अभ्यासाच्या दृष्टीने अधिक सुलभ असतात. द्वि- किंवा बहु-आणवीय वायूंच्या शोषण वर्णपटातील रेषा रुंद असतात, म्हणजेच ते अरुंद पट्टे असतात [→ वर्णपटविज्ञान].

उष्णता प्रारणाचे मापन : उष्णता प्रारणाचे गुणधर्म दृश्य प्रकाश प्रारणासारखेच आहेत फरक इतकाच की, त्याची तरंगलांबी अधिक असून ते डोळ्यांना दिसत नाहीत. त्यामुळे त्यांचा शोध घेण्यासाठी व त्यांच्या मापनासाठी दृश्य प्रकाशासाठी वापरतात त्याहून वेगळ्या प्रकारची उपकरणे वापरावी लागतात. या उपकरणांत प्रारणाच्या उष्णतेच्या उपयोग केला जातो. काही महत्त्वाची उपकरणे पुढे दिली आहेत:

(१) बोलोमीटर : हे उपकरण ‘लँग्‍ली बोलोमीटर’ या नावाने प्रसिद्ध आहे. १८८१ मध्ये लँग्‍ली यांनी ते प्रथम वापरले. नंतर माउंट विल्सन वेधशाळेच्या ॲबट यांनी त्यात सुधारणा केल्या.

यामध्ये मापनासाठी व्हिट्‍स्टन सेतू [विद्युत् राशी मोजण्याचे एक उपकरण, → व्हिट्स्ट‌न सेतु] वापरला असून त्याच्या समोरासमोरील बाजूंसाठी प्लॅटिनमाच्या सु. १२ मिमी. लांब, ०·०६ मिमी. रुंद व ०·००५ मिमी. जाड पट्टया वापरल्या जातात. यांपैकी एका पट्टीला प्रारणाच्या शोषणासाठी काजळी माखलेली असते व दुसर्‍या पट्टीला प्रारणाचा संपर्क होऊ नये म्हणून व्यवस्था केलेली असते. सेतूच्या उरलेल्या दोन बाजूंमध्ये रोधक तारांची वेटोळी असतात.

प्लॅटिनमाची अतिपातळ पट्टी तयार करण्यासाठी, एक प्लॅटिनमाची पातळ पट्टी व चांदीची किंचित पट्टी एकत्र झाळून व त्यावरून रूळ फिरवून, पट्टीची जाडी पाहिजे तेवढी कमी करतात. नंतर नायट्रिक अम्‍लात चांदी विरघळविली की, प्लॅटिनमाची अतिपातळ पट्टी प्राप्त होते.

प्रथम सेतू समतोल करून नंतर काजळी असलेल्या पट्टीवर प्रारण पाडले, तर पट्टीचे तापमान वाढते व त्याबरोबरच तिचा रोध वाढून पहिला समतोल ढळतो आणि त्यामुळे विद्युत् प्रवाहमापकाचा काटा विचलित होतो. तारांच्या वेटोळ्यांचा रोध जरूर तितका बदलून परत समतोल निर्माण करतात. यामुळे पट्टीच्या रोधातील वाढ कळते व त्यावरून तिला मिळालेली उष्णता मोजता येते. या उपकरणाला रैखिक उष्णतामापक म्हणतात. कृष्ण पदार्थाच्या वर्णपटातील ऊर्जा वितरण मोजण्यासाठी हे उपकरण वापरतात. पट्टीचे तापमान केवळ ०·०००१^० से. ने जरी वाढले, तरी ते मोजता येते इतके हे साधन संवेदनक्षम आहे.

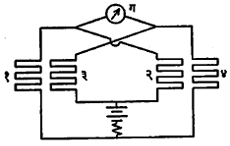
लुमर व कुर्लबॉम यांनी अधिक कार्यक्षम बोलोमीटर बनविला. (आ. ७) त्यातील प्रमुख सुधारणा अशा आहेत: (अ) प्लॅटिनमाची एकच पट्टी न वापरता अनेक पट्ट्यांचे जाळे वापरले व व्हिट्‍स्टन सेतूच्या चारी बाजूंसाठी वापरले. (आ.) पट्ट्यांची जाडी ०·०००५ मिमी. इतकी बारीक ठेवली. १ व ३ या बाजू काळ्या करून एकमेकींसमोर ठेवल्या असल्याने त्या दोन्ही उष्णतेचे शोषण करतात. २ व ४ या बाजूंना प्रारणाचा संपर्क न होईल अशी काळजी घेतलेली असते. १ व ३ या दोन्ही बाजूंचा रोध उष्णतेमुळे वाढतो व त्यामुळे ग या विद्युत्‌ प्रवाहमापकाचा काटा दुप्पट कलतो. या सर्व सुधारणांमुळे हे उपकरण अधिक कार्य़क्षम बनलेले आहे. याला ‘सरफेस बोलोमीटर’ म्हणतात.

(२) तपचिती : अँटिमनी व बिस्मथ किंवा बिस्मथ व चांदी या धातूंची अनेक तपयुग्मे जोडून ही चित्ती बनविलेली असते. सांध्यांच्या दोन बाजूंपैकी एका बाजूस काजळी माखलेली असते व त्यावर जेव्हा प्रारण पडते, तेव्हा त्याचे तापमान दुसर्‍या बाजूच्या मानाने वाढून तापविद्युत् निर्माण होते आणि तिची नोंद चितीला जोडलेल्या विद्युत् प्रवाहमापकाने होते. या मापकाचे अंशन केलेले असल्यामुळे त्याच्या नोंदीवरून उष्णतेचे मापन करता येते. हे उपकरण प्रथम मेलोनी यांनी बनविले. नंतर इतरांनी त्यात पुष्कळ सुधारणा करून ते अत्यंत कार्यक्षम केले. या बाबतीत कोब्‍लेंट्‍झ यांनी विशेष परिश्रम घेतले.

आधुनिक तपचिती घनाकृती असते. घनाच्या एका बाजूला उष्ण सांधे व विरूद्ध बाजूस थंड सांधे असतात. तपयुग्मासाठी वापरलेल्या पट्ट्यांचे थर एकमेकांपासून निरोधित होण्यासाठी त्यांच्यामध्ये मेणकागद किंवा अभ्रक यासारख्या विद्युत् निरोधकांचा उपयोग केलेला असतो. घनाच्या थंड सांध्यांच्या बाजूवर एक धातूचे टोपण बसविलेले असते व उष्ण, सांध्याच्या बाजूवर एक सैंधवाचे आवरण बसविलेले असते. उपकरण जेव्हा उपयोगात नसते, तेव्हा उष्ण सांध्यांच्या बाजूवरही धातूचे टोपण बसविलेले असते. संवेदनक्षमता वाढविण्यासाठी जर तपयुग्मांची संख्या अनिर्बंधपणे वाढविली , तर रोध वाढतो व एकंदर संवेदनक्षमता कमी होते. याकरिता तपयुग्मांची संख्या, त्यांचा एकूण रोध विद्युत् प्रवाहमापकाच्या रोधाइतका होईल, अशी ठेवलेली असते. उष्णता संवहन टाळण्यासाठी सांधे व जोडतारा यांची जाडी अतिशय कमी ठेवलेली असते. तसेच उष्णतेचे संनयन टाळण्यासाठी उपकरण निर्वात पेटीमध्ये ठेवलेले असते. या उपकरणाचा प्रमुख दोष म्हणजे ते कार्यवाहीत आणण्यास व पुन्हा पूर्वस्थितीप्रत नेण्यास फार वेळ लागतो.

(३) प्रारण सूक्ष्ममापक : बॉईज यांनी हे उपकरण तयार केले. यामध्ये अँटिमनी व बिस्मथ यांचे एकच तपयुग्म वापरलेले असते. युग्माचा सांधा काजळी माखलेल्या एका तांब्याच्या लहान चकतीला जोडलेला असतो. चकतीवर जेव्हा प्रारण पडते,तेव्हा चकतीला जोडलेला तपयुग्मचा सांधा तापतो व त्यामुळे तापविद्युत् निर्माण होते. युग्माची दुसरी टोके एका तांब्यांच्या वेटोळ्याला जोडलेली असतात व हे वलय एका स्थिर चुंबकाच्या चुंबकीय क्षेत्रात क्वार्ट्‌झाच्या बारीक धाग्याने टांगलेले असते. तारेचे वेटोळे व क्वार्ट्‌झाचा धागा यांमध्ये काचेची एक पातळ पट्टी वापरलेली असते व तिच्यावर एक छोटा आरसा बसविलेला असतो. आरशावर टाकलेल्या प्रकाशकिरणांमुळे निर्माण होणार्‍या उष्णतेचा तपयुग्माशी संपर्क होऊ नये म्हणूनच केवळ काचेची पट्टी वापरतात. प्रारण जेव्हा तांब्याच्या चकतीवर पडते, तेव्हा वेटोळ्यात विद्युत् प्रवाह वाहू लागतो व भोवतीच्या चुंबकीय क्षेत्रामुळे ते वेटोळे फिरते व वेटोळ्याबरोबर आरसाही फिरल्यामुळे त्यावरून परावर्तित होणारी किरणशलाकाही फिरते. ही परावर्तित किरणशलाका एका मोजपट्टीवर पडत असल्याने वेटोळ्याचे परिभ्रमण मोजता येते व त्यावरून प्रारणाचे मापन करता येते.

तप्तयुग्माच्या तारा चुंबकीय असल्याने त्या शक्य तितक्या चुंबकापासून दूर ठेवलेल्या असतात व त्यांचे चुंबकीय क्षेत्रापासून रक्षण व्हावे म्हणून त्यांच्याभोवती मृदू लोखंड ठेवतात. तांब्याच्या तारेचे वेटोळे अचुंबकीय करण्यासाठी विट यांनी पुढील पद्धत वापरली : सर्वसाधारण तांबे समचुंबकीय (निर्वातापेक्षा जास्त चुंबकीय पार्यता असलेले) असते, तर विद्युत् विच्छेदनी (विद्युत्‌ प्रवाहाने तांब्याच्या संयुगाच्या विद्रावाचा विच्छेद करून मिळविलेले) तांबे प्रतिचुंबकीय (निर्वातापेक्षा कमी चुंबकीय पार्यता असलेले) असते. म्हणून सर्वसाधारण तांब्याच्या तारेचे वेटोळे प्रथम नायट्रिक अम्‍लात घालून त्यावर नंतर विद्युत् विच्छेदनी तांब्यांचा योग्य प्रमाणात मुलामा दिला. तर तांब्याच्या तारेचे अचुंबकीय वलय बनू शकते.

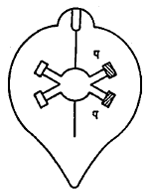
(४) क्रुक्स यांचा प्रारणमापक : (आ. ८) यामध्ये अँल्युमिनियमाच्या दोन हलक्या पट्ट्या प –प एकमेकींशी काटकोन करून बसविलेल्या असून त्यांच्या टोकांना कथिल अथवा अभ्रकाची पातळ पाती जोडलेली असतात व त्यांच्या एका अंगाला काजळी माखलेली असते. उदग्र (उभ्या) अक्षाभोवती पट्ट्या परिभ्रमण करू शकतात. अशा रीतीने या सर्व गोष्टी एका साधारण निर्वात अशा काचेच्या गोलात बसविलेल्या असतात.प्रारण जेव्हा पात्यावर पडते, तेव्हा पात्याचे काळे पृष्ठभाग उष्णता शोषतात व त्यामुळे ते तापतात. या काळ्या पृष्ठभागावर आदळणारे हवेचे रेणूही तापतात व त्यांचा दाब स्वच्छ पृष्ठभागावर आदळणार्‍या रेणूंपेक्षा अधिक होतो. यामुळे पाती फिरू लागतात. पात्यांच्या परिभ्रमण-वेगावरून प्रारणाची तीव्रता अजमावता येते. पाती क्वार्ट्‌झाच्या धाग्याने टांगलेली असतात व परिभ्रमणामुळे धाग्याला पीळ पडतो. पाती किती अंशात फिरतात, हे किरणशलाका व मोजपट्टी वापरून काढता येते व त्यावरून उष्णतेचे मापन करता येते. सर्वसाधारणपणे हा मापक प्रारणाचा फक्त शोध घेण्यासाठी वापरतात. निकोल्स यांनी त्यात सुधारणा करून तो अधिक कार्यक्षम केलेला आहे.

सौरांक : सूर्यापासून पृथ्वीकडे येणार्‍या किरणांपैकी बराचसा भाग पृथ्वीच्या वातावरणात परावर्तित होतो किंवा विखुरला जातो. वातावरणातील जलबाष्प,ढग व बर्फ हे चांगलेच परावर्तक आहेत. वातावरणातील धूलिकण व अणू यांमुळे किरणांचे प्रकीर्णन होते. याशिवाय २० ते ४० टक्के प्रारण वातावरणात शोषले जाते. हे शोषण ऋतुमान व दिवसाचा वेळ यांच्यावर अवलंबून असते. याप्रमाणे सूर्यापासून पृथ्वीवर पोहोचणारी उष्णता सर्व ऋतूंत व सर्व वेळी सारखी नसते. या उष्णतेच्या मापनासाठी एक स्थिरांक ठरविला आहे. त्याला सौरांक असे म्हणतात. त्याची व्याख्या पुढे दिल्याप्रमाणे केली जाते: ‘वातावरणात उष्णतेचे शोषण होत नाही, असे गृहीत धरून किंवा वातावरण नाहीच असे समजून, एक चौ. सेमी. क्षेत्रफळाचा कृष्ण पदार्थ जर सूर्यकिरणांना लंब राहील असा ठेवला व जर कृष्ण पदार्थाचे सूर्यापासूनचे अंतर सूर्य आणि पृथ्वी यांमधील सरासरी अंतराएवढे असले, तर दर मिनिटाला त्या पृष्ठभागाला मिळणार्‍या उष्णतेस सौरांक’ असे म्हणतात. तो कॅलरी/मिनिट या एककात मोजतात.

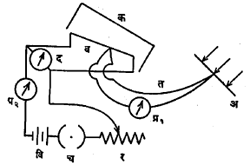
सौरांक मोजण्यासाठी अँगस्ट्रॉम यांनी एक सौरतापमापक तयार केला, त्याचे वर्णन पुढे दिले आहे: आ.९ मध्ये दाखविल्याप्रमाणे अ व ब च्या प्लॅटिनमाच्या किंवा मँगॅनिजाच्या एकसम पट्ट्या असून त्या काळ्या केलेल्या आहेत. अ पट्टीवर सूर्यकिरण लंब दिशेने पाडता येतात किंवा पट्टी झाकून तिच्यावर किरण पडणे बंदही करता येते. क या पडद्यामुळे ब पट्टीवर सूर्यकिरण पडू शकत नाहीत. तांबे व कॉन्स्टंटन या धातूंचे एक तपयुग्म अ व ब यांच्या मागील बाजूस जोडलेले आहे. प्र१, हा विद्युत् प्रवाहमापक आहे. वि हा विद्युत् घट, प्र२ हा अँपिअरमापक व र हा रोध ब ह्यास एकसरीत (एका पुढे एक) जोडलेला आहे व च या चावीने विद्युत् प्रवाह सुरू किंवा बंद करता येतो. द हा व्होल्टमापक आडवा जोडलेला आहे.

विद्युत् प्रवाह बंद ठेवून अ वर सूर्यकिरण पडू दिले असता अ तापतो व तपयुग्मात विद्युत् प्रवाह निर्माण होऊन प्र_१ मधील दर्शनकाटा कलतो. आता ब मधून विद्युत् प्रवाह सुरू केला असता तो तापू लागतो. जेव्हा ब चे तापमान ब इतके होते तेव्हा तपयुग्मातील विद्युत् प्रवाह बंद होतो व प्र१ चा दर्शककाटा पुन्हा शून्यावर येतो. ब मधील विद्युत् प्रवाह प्र_२ ने व विद्युत्‌ दाब द ने मोजल्याने ब ला मिळालेली उष्णता काढता येते व ती अ ला मिळालेल्या उष्णतेएवढी अर्थातच असते. जर दर मिनिटास दर (सेंमी.)^२ पृष्ठभागाला मिळणारी उष्णता S असेल तर S हे सौरांकाचे मूल्य होते. पण यात वातावरणात होणार्‍या शोषणाबद्दल दुरुस्ती करणे जरूर आहे. यासाठी बुगेअर यांनी वरील प्रयोग दिवसाच्या निरनिराळ्या वेळी करून पुढील समीकरण मिळविले :

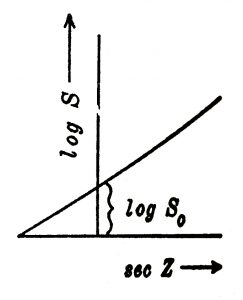
S = S o a ^secZ      …        …        …       (१७)

यात a हा प्रेषण गुणांक असून तो ०·५५ ते ०·८५ आहे. Z हे सूर्याचे अंशात्मक अंतर आहे. यावरून log S = log So + secZ log a … (१७ अ) हे समीकरण मिळते. आता secZ व log S यांचा आलेख काढला (आ.१०) तर त्यावरून log So व म्हणून So हा सौरांक मिळतो.

लँग्‍ली यांनी असे प्रतिपादले की, काही एकवर्णी प्रारण वातावरणात संपूर्णपणे शोषले जाणे शक्य असल्याने वरील पद्धतीने मिळालेले सौरांकाचे मूल्य काहीसे कमी असणार .या गोष्टीचा विचार करून ॲबट यांनी पुढील पद्धती वापरली.

अवकाशातील वातावरणाची स्थिती शक्य तितकी स्थिर असताना वर्णपट बोलोमीटरने सूर्याच्या संपूर्ण वर्णपटातील ऊर्जा वितरणाचा अँबट यांनी आलेख काढला. त्याच वेळी सूर्याची संपूर्ण प्रारण ऊर्जा सौरतापमापकाने मोजली. नंतर बुगेअर यांच्या समीकरणाचा उपयोग करून वातावरणविरहित अवस्थेतील ऊर्जा वितरणाचा आलेख मिळविला. प्रत्यक्ष मिळालेला आलेख व तळरेषा यांच्यामधील क्षेत्रफळ A आहे व वातावरणविरहीत अवस्थेतील आलेख व तळरेषा याच्यामधील क्षेत्रफळ Ao आहे असे समजल्यास सौरांक

So = S Ao/A     …       …      (१८)

या समीकरणाने मिळतो. सौरांकाचे मूल्य त्याच्या सरासरी मूल्याच्या १/२० ने बदलत असते. हा बदल सूर्याच्या प्रारणात होणार्‍या बदलामुळे होतो की वातावरणातील घटक व पारदर्शकता यांत होणार्‍या फेरफारामुळे होतो, हे तितकेसे स्पष्ट झालेले नाही. सूर्यावरील डागांचा या बदलाशी संबंध असावा, असे मत मांडण्यात आलेले आहे.

सूर्याचे तापमान : सूर्याचा मध्यभाग (गाभा) अति-उष्ण असून त्याच्या भोवतीचा दीप्तिगोल त्या मानाने कमी उष्ण आहे. या दीप्तिगोलाचे तापमान पुढे दिल्याप्रमाणे काढता येते. सूर्य हा कृष्ण पदार्थाप्रमाणे पूर्ण उत्सर्जक आहे व त्यापासून दर सेकंदास उत्सर्जित होणारी उष्णता H आहे, असे समजू त्याचे तापमान T⁰ के. आहे व त्रिज्या r आहे, असेही समजू तर H = 4πr² o T⁴जर पृथ्वीचे सूर्यापासूनचे अंतर R असेल, तर

 व म्हणून

यावरून T = ५,७३२^० के. असे सूर्याचे तापमान मिळते.

वीन यांच्या λm T = b = ०·२८९७ सेंमी., ^०के. या समीकरणात λm= ४,७५३ × १०^-८ सेंमी, हे मूल्य वापरून ॲबट यांनी T = ६,०६०^० के. सूर्याचे तापमान काढले. याला वर्णपट तापमान म्हणतात.

सौरांकावरून काढलेले तापमान सु. ३००^०के. ने कमी आहे. याचे कारण म्हणजे सूर्य कृष्ण पदार्थासारखा पूर्ण उत्सर्जक आहे, हे अनुमान बरोबर नाही.

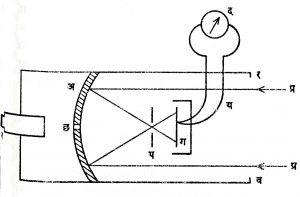
उत्तापमापक : कृष्ण पदार्थापासून उत्सर्जित होणारे प्रारण त्याच्या तापमानावरच केवळ अवलंबून असते, हे श्टेफान यांच्या Eα T⁴ या नियमावरून स्पष्ट दिसते. म्हणून कृष्ण पदार्थाची प्रारण ऊर्जा माहीत झाल्यास त्याचे तापमान काढता येईल. या तत्त्वावर आधारलेले उत्तापमापक हे उपकरण तापमान मोजण्यासाठी वापरता येते. ही तापमापके दोन प्रकारची आहेत (१) समग्र प्रारण उत्तापमापक यात प्रारणाची समग्र ऊर्जा मोजून तापमान काढले जाते. (२) प्रकाशीय उत्तापमापक : यात प्रारणाच्या वर्णपटातील एका विभागाची ऊर्जा मोजून व प्लांक यांच्या नियमाचा उपयोग करून तापमान काढले जाते. उत्तापमापकाचा प्रमुख दोष म्हणजे तो फक्त कृष्ण पदार्थाचेच तापमान बरोबर मोजू शकतो. पदार्थ जर कृष्ण पदार्थ नसेल, तर तापमापकाने दर्शविलेले तापमान हे तेच प्रारण उत्सर्जित करणार्‍या कृष्ण पदार्थाचे तापमान असते. याला कृष्ण पदार्थ तापमान म्हणतात. हे पदार्थाच्या प्रत्यक्ष तापमानापेक्षा कमी असते.

सर्वसाधारणपणे ही तापमापके ६००^० से. हून अधिक तापमान मोजण्यासाठी वापरतात. त्यांची थोडक्यात माहिती अशी :

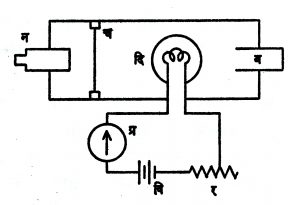
समग्र प्रारण उत्तापमापक : सु. १,४००^० से. पर्यंतचे तापमान याने मोजता येते. आ. ११ मध्ये दाखविल्याप्रमाणे अ या अंतर्गोल आरशावरून प्रारण परावर्तित होते. हा आरसा मागेपुढे सरकविता येत असल्याने परावर्तित प्रारण ग या ग्राहकावर केंद्रित करता येते. ग्राहकाला काजळी माखलेली असते. प हा एक चकचकीत पडदा असून तो दोन अर्धगोलांचा केलेला आहे. हे अर्धगोल एकमेकांशी किंचित (५^०) कोन करून ठेवलेले असतात. ग्राहकाला य या तपयुग्माचा एक सांधा जोडलेला असतो व तापविद्युत् वर्चस् (व्होल्टेज) द या मिलिव्होल्टमापकाने मोजता येते.

र–व द्वाराने येणारे प्रारण अ या अंतर्गोल आरशाने प वर केंद्रित होते. केंद्रीकरण जेव्हा व्यवस्थित होते, तेव्हा दोन्ही अर्धगोल आ.१२ मध्ये दाखविल्याप्रमाणे नीट सांधलेले दिसतात; पण केंद्रीकरण नीट न झाल्यास, आ. १३ मध्ये दाखविल्याप्रमाणे अर्धगोल एकमेकांपासून ढळलेले दिसतात.

अ मध्ये छ हे छिद्र असल्याने न या नेत्रभिंगातून अर्धगोल पाहता येतात. द ने दर्शविलेले विद्युत् वर्चस् ग ला मिळालेल्या उष्णतेच्या तीव्रतेवर अवलंबून असते. प्रारणाच्या उगमस्थानापासून निघालेली सर्वच उष्णता ग ला मिळत असल्याने उष्णतेची तीव्रता आणि उगमस्थान ग यांमधील अंतरावर अवलंबून राहत नाही. जर उगमस्थान व ग्राहक यांचे तापमान अनुक्रमे T⁰ के. व To ⁰ के. असेल आणि व्होल्टमापक V वर्चस् दाखवीत असेल, तर

V = a (T^b –T_o^b)        …           …          (२०)

हे समीकरण मिळते. येथे a हा स्थिरांक असून b चे मूल्य ३·८ ते ४·२ इतके आहे. b चे मूल्य बरोबर ४ नसण्याची कारणे अशी आहेत : (१) तपयुग्माच्या दोन्ही सांध्यांच्या तापमानांतील फरकाच्या बरोबर प्रमाणात वर्चस् असत नाही; (२) तुरळक परावर्तन व (३) जोडतारातून होणार्‍या उष्णता संवहनामुळे थंड सांध्याचे तापमान थोडे वाढते. या दोषास्तव या तापमापकाचे अंशन दुसर्‍या प्रमाण तापमापकाच्या साहाय्याने प्रथम करावे लागते.

प्रकाशीय उत्तापमापक : यामध्ये कृष्ण पदार्थापासून निघालेल्या प्रारणापैकी λ व λ + dλ या तरंगलांबींच्या मर्यादेतील प्रारणाची ,एका प्रमाण प्रकाश उगमापासून (दिव्यापासून) निघालेल्या त्याच मर्यादेतील प्रारणाशी तुलना केली जाते. समजा, कृष्ण पदार्थाची व दिव्याची उत्सर्जन ऊर्जा अनुक्रमे E₁ व E₂ आहे. आणि त्यांचे तापमान अनुक्रमे T₁ व T₂ आहे. तरंगलांबीचा पट्टा लहान असल्याने प्लांक यांच्या सिद्धांताऐवजी वीन यांचा सिद्धांत येथे वापरता येतो. आता वीन यांच्या सिद्धांताप्रमाणे :

 

हे समीकरण मिळते; यावरून T₁ चे मूल्य काढता येते.

प्रकाशीय उत्तापमापक दोन प्रकारचे असतात, ते प्रकार असे : (१) अदृश्य होणारा तंतू असलेला प्रकाशीय उत्तापमापक : (आ. १४). यात ब हे एका दूरदर्शकाचे (दुर्बिणीचे) वस्तुभिंग प्रकाश उगमस्थानाची (ज्याचे तापमान मोजावयाचे त्याची) प्रतिमा दि या दिव्याच्या तंतूवर पडते. ही प्रतिमा च या रक्तवर्ण गाळणीतून न या नेत्र भिंगाने पाहता येते. आ.१४ मध्ये वि. विद्युत्‌ घटमाला प्र विद्युत्‌ प्रवाहमापक आणि र बदलता येणारा रोध असून ते दिव्याच्या तंतूसह एकसरीत जोडलेले आहेत. प्रत्यक्ष प्रयोगात दिव्याचा तंतू दिसेनासा होईतो र च्या साहाय्याने मंडलातील विद्युत् प्रवाह कमीजास्त करावयाचा असतो. गाळणीमुळे विशिष्ट तरंगलांबीच्या टप्प्यातील तरंगांवर प्रयोग करता येतो. निरनिराळ्या उगमस्थानाचे तापमान प्रमाण तपयुग्मांनी मोजून व ही ज्ञात तापमाने आणि विद्युत् प्रवाह यांचा आलेख काढून, या उपकरणांचे अंशन परीक्षण करता येते. (२) ध्रुवित प्रकाश उत्तापमापक : यामध्ये दिव्यापासून निघणारे किरण व उगमस्थानापासून निघणारे किरण यांचे एकमेकांशी काटकोनात ध्रुवण केलेले असते. दोहोंचा प्रत्येकी अर्धवर्तुळाकृती प्रकाश गाळणी व निकल लोलक यांमधून नेत्रभिंगाकडे जातो. प्रथम निकल लोलक फिरवून दिव्यांचा प्रकाश बंद होईल असे करावे. नंतर तो पुन्हा फिरवून दोन्ही प्रकाशांची तीव्रता सारखी करावी. यासाठी जर निकल कोनातून फिरवावा लागत असला व जर उगमाचे तापमान T⁰ के. असले, तर

log tan ∅ = a+ b/T      …           …         (२२)

या समीकरणाने T काढता येते. a व b हे स्थिरांक आहेत. त्यांची मूल्ये ज्ञात करून घेण्यासाठी या मापकाचे अंशन परीक्षण करणे आवश्यक आहे.

संदर्भ : 1. Ghosh, S. N.; Deb, S. Heat, Calcutta, 1963.

2. Noakes, G. R. A Textbook of Heat, London, 1960.

3. Saha. M. N.; Shrivastav, B. N. A Treatise on Heat, Allahabad and Calcutta, 1965.

देशपांडे. अ. शा.