आलेख: दोन अथवा अधिक संचांमधील (माणसे, वस्तू, त्यांचे विविध गुणधर्म इत्यादींच्या समूहांमधील) परस्परसंबंधांचे भूमितीय चित्रण म्हणजे आलेख होय. उपलब्ध माहिती (उदा., एखाद्या देशाची कालमानानुसार लोकसंख्या, औषधाचे प्रमाण व त्याचा रुग्णाच्या रक्तस्रावावर होणारा परिणाम इ.) आलेखाच्या साहाय्याने सहजपणे समजेल अशी मांडता येते आणि त्याचा अभ्यास करून निष्कर्ष काढणे सुलभ होते. आलेख काढण्याच्या विविध पद्धती आहेत. उपलब्ध माहितीचा प्रकार, अपेक्षित अचूकता इ. बाबींचा विचार करून आलेख काढण्याची पद्धती निश्चित करावी लागते.
जात्याक्ष आलेख : या पद्धतीत एक आडवी व दुसरी उभी अशा दोन एकमेंकाना काटकोनात छेदणाऱ्या सरळ रेषा संदर्भ-अक्ष म्हणून निवडतात. आडव्या रेषेस क्ष अक्ष व उभ्या रेषेस य अक्ष म्हणतात. त्यांच्या छेदनबिंदूस आदिबिंदू आ म्हणतात. ज्या माहितीचा आलेख काढावयाचा असेल त्यावरून सोईस्कर अशा प्रमाणाची निवड करून त्याप्रमाणे क्ष आणि य अक्षांवर खुणा करून घेतात. क्ष आणि य अक्षांसाठी एकच प्रमाण असण्याची जरुरी नाही, तर प्रसंगी ते वेगळेही घेणे आवश्यक ठरते. क्ष अक्षावर आदिबिंदूच्या उजवीकडील अंतरांची चिन्हे धन व डावीकडील ऋण, तर य अक्षावर आदिबिंदूच्या वरील अंतरे धन आणि खालील ऋण मानण्याचा संकेत आहे. समजा, क्ष हा {क्ष१, क्ष२,……,क्षप} संच असून त्यातील
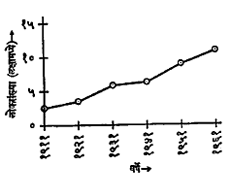
घटकांशी संगत असे य, संचातील अनुक्रमे य१, य२, …….यप हे घटक आहेत. अक्षांवरील प्रमाण निवडताना क्ष१ ते क्षप यांचे निदर्शक सर्व बिंदू क्ष अक्षावर आणि य१ ते यप यांचे निदर्शक सर्व बिंदू य अक्षावर म्हणजेच आलेखपटावर घेता येतील, अशी काळजी घेणे जरूर आहे. आता क्ष१ या क्ष अक्षावरील बिंदूमधून य अक्षास समांतर रेषा काढली आणि य१ या य अक्षावरील बिंदूतून क्ष अक्षास समांतर रेषा काढली, तर या दोन्ही रेषा जेथे छेदतील त्या बिंदूस ब१(क्ष१, य१) असे नाव दिल्यास क्ष१ आणि य१ यांना ब१ या बिंदूंचे अनुक्रमे क्ष-सहनिर्देशक आणि य-सहनिर्देशक म्हणतात. याचप्रमाणे ब२(क्ष२, य२), ब३(क्ष३, य३),……, बप(क्षप, यप) असे एकूण प बिंदू मिळतील. हे सर्व बिंदू एकापुढे एक असे सरळ रेषांनी साधले असता पाहिजे असलेला आलेख मिळतो. आ. १ मध्ये क्ष अक्षावर वर्षे व य अक्षावर एका शहरातील संगत लोकसंख्या घेऊन काढलेला आलेख दर्शविला आहे.
समीकरणाचा निदर्शक आलेख : समजा,य = फ (क्ष) असे समीकरण आहे. येथे फ(क्ष) हे फलन (य आणि क्ष मधील परस्पर संबंध दर्शविणारी राशी) बैजिक, त्रिकोणमितीय वा अन्य काही प्रकारचे अबैजिक फलन असू शकेल. समजा, हे फलन क ≤ क्ष ≤ ख या अंतरालासाठी व्याख्यात (म्हणजे फलनाचे मूल्य मांडता येईल असे) आहे. आता क्ष अक्षावर दिलेल्या अंतरालातील काही बिंदू क्ष१, क्ष२,……,क्षप घेऊन त्यांना संगत अशी य ची मूल्ये य = फ(क्ष) या दिलेल्या समीकरणावरून काढतात. ही अनुक्रमे फ (क्ष१), फ(क्ष२),……, फ(क्षप) अशी लिहून वर वर्णन केल्याप्रमाणे
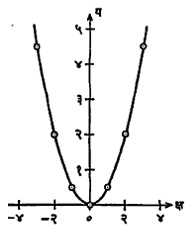
आलेखपटावर ब१ [क्ष१, फ(क्ष१)], ब१ [क्ष२, फ(क्ष२)],……., बप [क्षप, फ(क्षप)], असे बिंदू स्थापतात. वरील उदाहरणात असे बिंदू सरळ रेषांनी सांधून आलेख मिळविला होता, पण समीकरणावरून काढावयाच्या या आलेखात तसे करत नाहीत. कारण येथे क्ष ची जी मूल्ये क्ष१, क्ष२,……इ. घेऊन या बिंदूंची स्थापना केली, त्यांतील कोणत्याही दोन मूल्यांच्या मधे क्ष ची अनंत मूल्ये असणे शक्य आहेत. अर्थात क्ष च्या शक्य असलेल्या प्रत्येक मूल्यासाठी जर बिंदूची स्थापना करावयाची म्हटले, तर अनंत बिंदू काढावे लागतील. हे प्रत्यक्षात करणे अशक्यप्राय असल्याने ह्यातील जे काही बिंदू मिळाले आहेत त्यांच्या अधले मधले इतर बिंदू कल्पनेनेच अस्तित्वात आहेत असे समजून आणि फ(क्ष) हे फलन संतत [ → फलन ] आहे असे गृहित धरून, जे ब१, ब२,…… इ. बिंदू प्रत्यक्ष काढले आहेत त्यामधून जाणारा एक मुक्तहस्त वक्र (हातानेच सहजगत्या काढलेला वक्र) काढतात. या वक्रास य = फ (क्ष) या दिलेल्या समीकरणाचा निदर्शक वक्र (आलेख) म्हणतात. या वक्राची गणितीय व्याख्या अशी : ज्या बिंदू संचातील प्रत्येक बिंदूचे सहनिर्देशक (क्ष, य) हे य = फ(क्ष) या समीकरणाची पूर्तता करतात, त्यास य = फ (क्ष) या समीकरणाचा निदर्शक वक्र म्हणतात. आ.२ मध्ये य = १/२ क्ष२ या समीकरणाचा निदर्शक वक्र दाखविला आहे. दिलेले समीकरण जर एकघाती असेल, तर निदर्शक वक्र सरळ रेषा असतो व जर ते द्विघाती असेल, तर निदर्शक वक्र शांकव असतो [→ वक्र शंकुच्छेद ].
वक्र अन्वायोजन :क्ष आणि य यांमधील संबंध समीकरणरूपाने दिलेला असल्यास त्याचा आलेख वर वर्णिल्याप्रमाणे काढता येतो. याच्या उलट
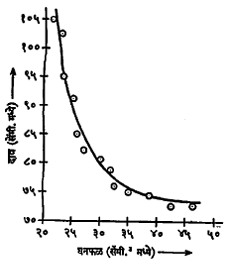
बऱ्याच वेळा हे समीकरण अगोदर माहीत नसून ते शोधून काढावयाचे असते. याकरिता प्रयोगाद्वारे मिळालेल्या निरीक्षणांवरून आलेखपटावर बिंदूंची स्थापना करतात व त्यांच्याशी जास्तीत जास्त मिळता जुळता असा मुक्तहस्त वक्र काढतात. या वक्राचे समीकरण म्हणजेच पाहिजे असलेले सूत्र होय. यालाच वक्र अन्वायोजन म्हणतात. आ.३ मध्ये तपमान कायम असताना वायूचा दाब आणि त्याचे घनफळ यांमधील संबंध शोधून काढण्यासाठी केलेल्या प्रयोगाच्या निरीक्षणांच्या आधारे स्थापन केलेले बिंदू व त्यांच्याशी जुळणारा वक्र दाखविला आहे. या वक्राचे समीकरण दाब × घनफळ = स्थिरांक (स्थिर संख्या) असे मिळते.
अंतर्वेशन व बहिर्वेशन : आ.१ मध्ये दाखविलेल्या आलेखाच्या साहाय्याने मधल्याच एखाद्या वर्षाची (उदा., १९४५) लोकसंख्या काय असेल याचे अनुमान काढता येते. यास अंतर्वेशन म्हणतात. तसेच त्यापुढील एखाद्या वर्षाची (उदा., १९६७) लोकसंख्या काय असेल याचा अंदाजही करता येईल. यालाच बहिर्वेशन म्हणतात [→ अंतर्वेशन व बहिर्वेशन].
आलेख व समीकरणांचे निर्वाह : आलेखाच्या साहाय्याने युगपत् समीकरणे सोडविता येतात. उदा., फ(क्ष, य) = ० आणि ग(क्ष, य) = ० अशी दोन समीकरणे दिलेली असल्यास व त्या दोन्ही समीकरणांचे निदर्शक आलेख काढले असता ते एकमेंकास जेथे छेदतील, त्या बिंदूचे सहनिर्देशक (क, ख) असल्यास क्ष = क आणि य = ख हे त्या समीकरण युग्माचे निर्वाह (समीकरण सोडवून आलेली उत्तरे) आहेत , हे उघड आहे. जर हे वक्र एकाहून अधिक बिंदूंमध्ये एकमेंकास छेदत असतील, तर तितके निर्वाह मिळतील.
जर फ(क्ष) = ० असे समीकरण असले, तर त्याचे निर्वाहही आलेखाच्या साहाय्याने काढता येतात. अशा समीकरणाचे निर्वाह म्हणजे य = फ(क्ष) आणि य = ० या दोन वक्रांच्या छेदनबिंदूंचे सहनिर्देशक होत. य = ० हे क्ष अक्षाचे समीकरण असल्यामुळे य=फ(क्ष) हा वक्र क्ष अक्षाला जेथे छेदत असेल, त्या बिंदूंचे सहनिर्देशक म्हणजेच हवे असलेले निर्वाह होत.
एखाद्या फ(क्ष) या दिलेल्या फलनाच्या गुणधर्माचा अभ्यास आलेखाच्या साहाय्याने सुलभपणे करता येतो. य = फ(क्ष) या समीकरणाचा निदर्शक वक्र काढून फ (क्ष) कोणत्या क्ष मूल्यासाठी शून्य होते, कोठे लघुतम वा महत्तम होते इ. बाबींचा अभ्यास करता येतो.
अवकल समीकरणांच्या [ → अवकल समीकरणे ] बाबतीतही त्यांच्या निर्वाहासंबंधी सर्वसाधारण अंदाज आलेखाच्या साहाय्याने करता येतो. समजा, फ(क्ष, य, य’) = ० हे अवकल समीकरण दिलेले आहे.
|
( य’ = |
d य |
) |
|
d क्ष |
आलेखपटावर ब (क, ख) हा कोणताही बिंदू घ्या. दिलेल्या समीकरणावरून क्ष = क आणि य = ख असता य’ चे मूल्य काढा. य’ हा अवकलज [ → अवकलन व समाकलन ] उतार निदर्शक असल्याने ब (क, ख) पासून य’ उतार असणारी एक अल्पांतरी सरळ रेषा ब ब१ काढा. आता ब१ च्या सहनिर्देशकांचा उपयोग करून दिलेल्या समीकरणाच्याच साहाय्याने य’ चे मूल्य काढा. या मूल्याइतका उतार असणारी एक अल्पांतरी रेषा ब१ ब२ काढा. असेच पुन्हा पुन्हा करीत राहिल्यास बब१, ब१ब२,….. या अल्पांतरी रेषांनी बनलेला वक्र सूचित होतो. हा वक्र मुक्तहस्ताने संतत असा काढा. हा वक्र म्हणजेच दिलेल्या अवकल समीकरणाच्या विशिष्ट निर्वाहाचा निदर्शक वक्र होय. ब ऐवजी दुसरा बिंदू घेतल्यास दुसरा एक वक्र मिळेल. अशा रीतीने वेगवेगळे बिंदू घेऊन वक्र मिळविल्यास एक वक्र मालिका मिळेल. त्यावरून अवकल समीकरणाचा सामान्य निर्वाह काढता येईल. या वक्र मालिकेला अन्वालोप असण्याची म्हणजेच दिलेल्या अवकल समीकरणास एकमात्र निर्वाह असण्याची शक्यता असल्यास तो कसा आहे हे अजमाविण्यास आलेखाची मदत होते.
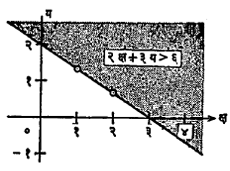
असमांचे आलेख : समीकरणांच्या आलेखाप्रमाणेच असमांबाबतही (राशींमधील असमान संबंध) आलेख काढता येतात. जर फ(क्ष, य) < क अशी असमा असेल, तर ज्या संचातील प्रत्येक बिंदूंचे सहनिर्देशक या असमेची पूर्ती करतील असा बिंदुसंच म्हणजे दिलेल्या असमेचा आलेख होय. आ.४ मध्ये २क्ष + ३य > ६ या असमेचा आलेख दर्शविला आहे. छायांकित भाग असमा निदर्शक बिंदुसंच दर्शवितो.
अनेकमितीय जात्याक्ष आलेख: द्विमिती जात्याक्ष आलेखाची संकल्पना अधिक व्यापक अर्थाने वापरली असता त्रिमिती जात्याक्ष आलेख मिळेल. आदिबिंदूतून जाणारा आणि क्ष व य ह्या दोन्ही अक्षांना लंब असणारा तिसरा झ हा अक्ष घेतल्यास त्रिमिती अवकाशाकरिता जात्याक्ष संदर्भव्यूह तयार होतो. अवकाशातील कोणत्याही बिंदूला (क्ष, य, झ) असे सहनिर्देशक दाखविता येतील. फ(क्ष, य, झ) = ० या समीकरणाची पूर्ती करतील असे (क्ष, य, झ) सहनिर्देशक असणाऱ्या सर्व बिंदूंचा संच म्हणजे फ(क्ष, य, झ) = ० या समीकरणाचा आलेख होय. यालाच समीकरणाचे निदर्शक पृष्ठ म्हणतात. हे समीकरण एकघाती असेल तर निदर्शक पृष्ठ प्रतल (पातळी) असून, द्विघाती असेल तर पृष्ठ शांकवज (शांकव वक्रांपासून तयार झालेली पृष्ठे) असेल. उठावाचा नकाशा हे त्रिमिती आलेखाचे उत्तम उदाहरण आहे. त्यामध्ये अक्षांश, रेखांश आणि उंची हे तीन संदर्भ-अक्ष असतात.
जर फ(क्ष, य, झ) > क ही असमा दिलेली असेल, तर निदर्शक बिंदुसंच वरीलप्रमाणे काढता येईल. उदा., क्ष२ +य२ + झ२ ≥ अ२ या असमेचा निदर्शक संच म्हणजे आदिबिंदू हे केंद्र आणि अ त्रिज्या असणारा भरीव गोल होय.
द्विमिती आलेखाच्या मानाने त्रिमिती आलेख काढण्यास आणि समजण्यास अवघड असल्याने त्याचा व्यवहारात फारसा उपयोग केला जात नाही. अधिक मितींकरिताही आलेख काढण्याची कल्पना करता येईल पण प्रत्यक्षात दाखविणे शक्य होणार नाही.
स्तंभ आलेख :क्ष-अक्षावर पाया असलेल्या सारख्या रुंदीच्या परंतु य-मूल्याच्या प्रमाणात उंची असलेले स्तंभ उभे करून उपलब्ध माहितीचे
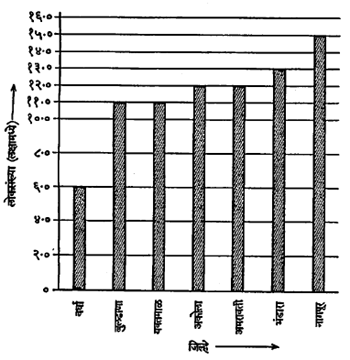
चित्रण करण्याची ही एक लोकप्रिय पद्धती आहे. स्तंभांऐवजी विविध प्रकारच्या आकृत्यांची (उदा., लोकसंख्या दाखविण्यासाठी माणसांच्या, विद्युत् शक्ती उत्पादन दाखविण्यासाठी मनोर्यांच्या इ.) योजना करण्यात येते. आ. ५ मध्ये महाराष्ट्रातील सात जिल्ह्यांची लोकसंख्या दर्शविणारा स्तंभ आलेख दाखविला आहे.
वर्तुळ आलेख : या पद्धतीत एक वर्तुळ घेऊन त्याचे वेगवेगळ्या त्रिज्यांच्या साहाय्याने निरनिराळ्या भागांत अशा तर्हेने विभाजन करतात की, प्रत्येक
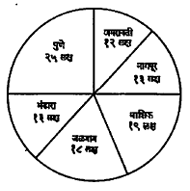
वर्तुळखंडाचे क्षेत्रफळ त्याच्याशी संबंधित असलेल्या मूल्याच्या प्रमाणात असते. उदा., एकूण अंदाजपत्रकातील खर्चांपैकी वेगवेगळ्या खात्यांकरिता करावयाचा खर्च वर्तुळखंडांच्या स्वरूपात दाखविता येईल. तौलनिक अभ्यासासाठी वर्तुळ आलेखाचा चांगला उपयोग होतो. आ. ६ मध्ये महाराष्ट्रातील सहा जिल्ह्यांची लोकसंख्या दर्शविणारा वर्तुळ आलेख दर्शविला आहे.
ध्रुवी आलेख : यामध्ये आलेखपटावर एक बिंदू व त्यामधून जाणारी एक रेषा संदर्भासाठी घेतात. त्यास अनुक्रमे ध्रुवबिंदू आणि संदर्भ रेषा असे म्हणतात. आलेखपटावरील कोणताही ब बिंदू घेतला आणि त्याचे ध्रुवबिंदू आ पासूनचे अंतर र असेल आणि आब ही रेषा संदर्भ रेषेशी थ कोन करीत
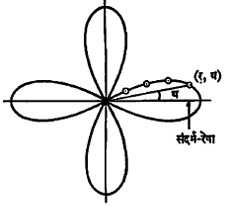
असेल, तर ब चे ध्रुवी सहनिर्देशक (र,थ) असतात. ज्याप्रमाणे जात्याक्ष आलेखपटावर बिंदू घेऊन आलेख काढतात तसेच या ध्रुवी पद्धतीतही आलेख काढतात. येथे प्रतिघटिवत (घड्याळातील काटे हलण्याच्या दिशेटच्या विरुद्ध) दिशेतील कोन धन मानतात. आ. ७ मध्ये र= कोज्या २ थ या समीकरणाचा आलेख दाखविला आहे.
त्रिमिती ध्रुवी आलेख हा द्विमिती आलेखाच्या संकल्पनेचाच पुढे विस्तार करून मिळतो. गोलीय ध्रुवी आणि चितीय ध्रुवी असे त्रिमिती ध्रुवी आलेखाचे दोन प्रकार आहेत [→ भूमिती].
अनुप्रयोग : कोणत्याही संकल्पनेचे भूमितीय घटकांच्या (बिंदू, रेषा इ.) साहाय्याने यथातथ्य चित्रण म्हणजे आलेख असे अधिक व्यापक अर्थाने म्हणता येईल. उदा., क्ष + i य, ( i = √ –१) ही मिश्रसंख्या [सदसत् संख्या, → संख्या] जात्याक्ष आलेखपटावर (क्ष,य) बिंदूने दर्शविता येते. अशा चित्रणाची मिश्रसंख्यांच्या अभ्यासाकरिता मदत होते.
वरील विवेचनावरून असे दिसून येईल की, जेथे उपलब्ध माहिती सहज आणि चटकन समजावी अशी अपेक्षा असेल तेथे आलेखाचा चांगला उपयोग होतो. उद्योगधंदे, जाहिराती, आर्थिक घडामोडी, शिक्षणक्षेत्र, सांख्यिकी, समाजशास्त्र इ. विविध क्षेत्रांत आलेख उपयुक्त ठरतात. गणितशास्त्रात फलनांचा अभ्यास आलेखाच्या उपयोगाने सुलभ होतो. अनुप्रयुक्त गणितात निरनिराळ्या समस्या आलेखाच्या आणि विश्लेषणाच्या साहाय्याने सोडविण्याच्या पद्धतींचा अभ्यास आलेखी विश्लेषणात होतो. कोणचाही सदिश (महत्ता व दिशा असलेली राशी) आलेखावर (जात्याक्ष किंवा ध्रुवी) दाखविता येत असल्यामुळे, त्याच्या मदतीने यामिकीतील [प्रेरणांची वस्तूंवर होणारी क्रिया व त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रातील,→ यामिकी] विविध समस्या सोडविता येतात. प्रेरणा, ताण, भार इ. राशी सदिशच असल्यामुळे स्थितिकीतील (यामिकी विषयाची एक शाखा) अभियांत्रिकीय प्रश्न आलेखाच्या साहाय्याने सोडविता येतात व या पद्धतीस आलेखीय स्थितिकी म्हणतात. मार्गनिर्देशन (विमानांचा वा जहाजांचा मार्ग निश्चित करणे) व सर्वेक्षण यांमधील प्रश्न सोडविण्यासाठी तसेच हवामानखात्यात दाब, तपमान, पर्जन्यमान इ. दर्शविण्यासाठी, मुलकी संरक्षण किंवा लष्करी डावपेचात, हवाई युद्धात शत्रूच्या विमानांच्या स्थानाचा व वेगाचा अंदाज करण्याकरिता, अणुस्फोटानंतर किरणोत्सर्गाचा परिणाम होणारे क्षेत्र समजण्यासाठी इ. विविध प्रकारे आलेखाचा उपयोग होतो.
काही समस्या सोडविण्याच्या बाबतीत आलेखाच्या साहाय्याने काढलेले निष्कर्ष जरूर तितके अचूक नसतात. अलीकडे संगणकाच्या (गणकयंत्राच्या) अधिकाधिक उपयोगामुळे अशा शास्त्रीय समस्या सोडविण्यामधील आलेखाचे महत्त्व कमी होत आहे.
गुर्जर, ल. वा. आगाशे, क. म.
“