आयनद्रायु भौतिकी

आयनद्रायु भौतिकी : एखाद्या वायूला प्रचंड प्रमाणात उष्णता देऊन त्याचे तपमान कित्येक लक्ष अंशांपर्यंत (के. केल्व्हिन तपमान एकक) वाढवले असता, त्यामधील अणूंचे विदलन होऊन (घटक मोकळे होऊन) त्यापासून ऋण आयन (विद्युत् भारित घटक) व धन आयन युग्मांची निर्मिती होते. अशा तऱ्हेने निर्माण झालेल्या पूर्ण आयनीकृत वायू-माध्यमास आयनद्रायू म्हणावे असे काही शास्त्रज्ञांचे मत आहे, तरी ज्या वायूत ऋण आणि धन आयन सर्वत्र सारख्या प्रमाणात आहेत व म्हणून तो विद्युत् वाहक आहे अशा सर्व प्रकारच्या माध्यमास आयनद्रायू ही संज्ञा देण्याचा प्रघात अलीकडे पडत चालला आहे. प्रायोगिक तंत्राच्या दृष्टीने आयनद्रायूचे दोन मुख्य विभाग पडतात : (१) उच्च तपमान आयनद्रायू, (२) लघू तपमान आयनद्रायू. पहिल्यास तीव्र (किंवा पूर्ण) आयनीकृत आयनद्रायू व दुसऱ्यास किंचित आयनीकृत आयनद्रायू असे म्हणतात. दुसऱ्या प्रकारामध्ये आयनीकरणाचे प्रमाण अल्प म्हणजे १ ते १० टक्क्यांपेक्षा जास्त नसते. पहिल्या प्रकारच्या आयनद्रायूत धन आयन व ऋण आयन हे दोनच घटक असतात, तर दुसऱ्या प्रकारात निर्विद्युत् अणू हा तिसरा घटक असून त्याचे संख्याबल सर्वांत जास्त असते. आयनद्रायूतील विद्युत् प्रवाहाची तीव्रता जर कमी असेल व त्यातील चुंबकीय क्षेत्राचे प्रमाण उपेक्षणीय असेल, तर अशा आयनद्रायूचे वर्णन ढोबळमानाने वायूंच्या रूढ गत्यात्मक सिद्धांतानुसार [→ द्रव्याचा गत्यात्मक सिद्धांत] करता येते. ज्या आयनद्रायूंचे चुंबकीय क्षेत्र तीव्र असते त्यासंबंधीचे विवेचन करण्याकरता   चुंबकीय द्रवगतिकी या शाखेची मदत घ्यावी लागते.

पूर्ण आयनीकृत आयनद्रायू ही पदार्थमात्राची सर्वांत विपुल व म्हणून महत्त्वाची अशी चौथी अवस्था आहे. पदार्थमात्राच्या घन, द्रव व वायू या तीन अवस्था सर्वांस ज्ञात आहेत. पदार्थास उष्णता दिली असता त्याचे एका अवस्थेतून दुसऱ्या अवस्थेत रूपांतर होते. याच न्यायाने वायूला उष्णता देऊन त्याचे तपमान कित्येक लक्ष के. अंशापर्यंत वाढविले असता त्याचे पूर्ण आयनीकृत आयनद्रायू या अंतिम अवस्थेत रूपांतर होते. मात्र हा बदल घडवून आणण्याकरिता लागणारी ऊर्जा ही पहिली दोन अवस्था संक्रमणे घडवून आणण्याकरिता लागणाऱ्या ऊर्जेपेक्षा कित्येक पटीने जास्त असते. अवकाशातील सूर्य व तत्सम तारे, ताऱ्यांचे अनेक समूह व दीर्घिका (आकाशगंगेसारखे प्रचंड तारासमूह) यांमधील वस्तुमात्र या पूर्ण आयनीकृत अवस्थेत आहेत. विश्वातील एकंदर वस्तुमात्राच्या ९९·९ टक्के भाग याच अवस्थेत असावा, असे शास्त्रज्ञांचे अनुमान आहे. इतक्या उच्च तपमानाचा आयनद्रायू संशोधनशाळेत निर्माण करण्याचे प्रयोग गेल्या काही वर्षांपासूनच चालू झाले आहेत व त्यांना अंशत:यशसुद्धा मिळाले आहे. हे प्रयोग जर यशस्वी झाले, तर सध्या जगापुढे असणाऱ्या ऊर्जेसंबंधीच्या कित्येक औद्योगिक व आर्थिक समस्या सुटतील. आयनद्रायूच्या साहाय्याने पाण्यापासून मिळणारा जड हायड्रोजन वापरून जीवनास आवश्यक अशी साधनसामग्री आपणास निर्माण करता येण्याची शक्यता आहे. पृथ्वीच्या सभोवताली कित्येक किलोमीटर उंचावर असलेले आयन वातावरणाचे पट्टे, उत्तर ध्रुवाजवळ दिसणारे विहंगम प्रकाशदृश्य [→ ध्रुवीय प्रकाश] ही सर्व नैसर्गिक आयनद्रायूंची उदाहरणे आहेत. बहुतेक घरांत आढळणाऱ्या निऑनाच्या दीप्तनलिका, हे मनुष्याने आपल्या उपयोगाकरिता निर्माण केलेल्या आयनद्रायूचे उदाहरण होय.

आयनद्रायूची गुणवैशिष्ट्ये : आयनद्रायूमध्ये धन आणि ऋण आयन हे सर्वत्र समप्रमाणात असतात. ऋण आयन बाहेर पडल्यानंतर राहिलेला वायूचा अणुभाग हाच आयनद्रायूमधील धन आयन असतो. काही अपवाद सोडले असता आयनद्रायूमधील ऋण आयन हा इलेक्ट्रॉनच असतो. हे दोन्ही प्रकारचे आयन इतस्तत: औष्णिक हालचालीत भाग घेत असल्यामुळे, वर वर्णिलेली आयनसंख्यासमता किंवा विद्युत् भारशून्यता ही स्थिती, पुरेसा मोठा अवकाश विभाग किंवा काल विभाग घेऊन, सरासरी काढली असतानाच बरोबर आढळेल, हे उघड आहे. ही विद्युत् भारशून्यतेची अट सरासरीने पाळली जाते असे दाखवता आले, तरी एखाद्या आयनाभोवती असणाऱ्या सूक्ष्म विभागात ही अट पाळली जाणार नाही, हे उघड आहे. आयनद्रायूमधील कोणताही एक आयन आपल्या भोवती विरुद्ध विद्युत् भार असलेल्या आयनांना आकर्षित करून त्यांचे एक वलय निर्माण करतो. प्रत्येक आयनाभोवती λ_D या डेबाय विद्युत् भार-आवरण-लांबीच्या अंतरात असलेल्या आयतनात (घनफळात) निर्माण होणाऱ्या विद्युत् क्षेत्राचे प्रमाण उपेक्षणीय असत नाही, असे आढळते. λ_D ची किंमत खाली दिलेल्या सूत्रावरून काढता येते.

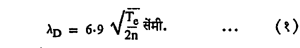
येथे T_e = इलेक्ट्रॉनाचे तपमान (के.), n = आयनांची आयतन घनता. अशाच प्रकारचे विद्युत् भार आवरण, आयनद्रायू धारकाच्या भिंतीजवळ किंवा आयनद्रायूमध्ये कोणतीही विजातीय वस्तू सोडली असता तिच्याभोवती निर्माण होते, असे दाखवणे शक्य आहे. आयनद्रायूमध्ये धन आयन, इलेक्ट्रॉन व निर्विद्युत् अणू या तीन घटकांचे एकमेकांवर आघात होतात व त्यामुळे त्यांच्यात गतिज ऊर्जेची देवघेव होते. अणू व धन आयन यांचे वस्तुमान जवळजवळ सारखेच असल्यामुळे त्यांच्यामध्ये गतिज ऊर्जेची देवघेव मोठ्या प्रमाणावर होऊन या दोन घटकांचे तपमान एकच होते. पण इलेक्ट्रॉनाचे वस्तुमान हे अणूच्या वस्तुमानापेक्षा कित्येक पटीने कमी असल्यामुळे, इलेक्ट्रॉन आपल्या गतिज ऊर्जेचा फारच थोडा अंश अणूला आघातानंतर देऊ शकतो. त्यामुळे इलेक्ट्रॉनाची आघातकंप्रता (दर सेकंदास होणाऱ्या आघातांची संख्या) जास्त नसेल, तर त्याची सरासरी ऊर्जा आणि तपमान, अणूच्या या राशींच्या अनेक पटीने जास्त असू शकते. ज्या आयनद्रायूकरिता T_{e &gt&gt} T_g (T_g म्हणजे अणूचे तपमान) ही स्थिती असते अशा आयनद्रायूला क्रियाशील आयनद्रायू म्हणतात. वायूचा दाब वाढवून जर इलेक्ट्रॉन व निर्विद्युत् अणू यांमध्ये होणाऱ्या आघातांची कंप्रता वाढवली, तर काही मर्यादेनंतर T_e = T_g अशी स्थिती निर्माण होते. ज्याच्यात अशा प्रकारचा औष्णिक समतोल प्रस्थापित झाला आहे अशा आयनद्रायूस औष्णिक आयनद्रायू अशी संज्ञा देतात. वर वर्णिलेल्या दोन्ही प्रकारच्या आयनद्रायूंमध्ये धारक भिंतीकडे जाणारी इलेक्ट्रॉन व धन आयनांची संख्या या सर्व परिस्थितीत नेहमीच विषम राहील असे दाखवता येते. याचा परिणाम असा होतो की, भिंतीवर त्यामुळे ऋण विद्युत् भार जमत जाऊन ऋण विद्युत् दाब निर्माण होतो. स्थिर स्थितीमध्ये या विद्युत् दाबामुळे दोन्ही प्रकारच्या आयनांच्या प्रवाहघनता सम होतात. या सर्व क्रियेमुळे, भिंतीजवळ डेबाय-आवरण-लांबी एवढे एक विद्युत् भारित वलय निर्माण होते. कोणतेही भिन्न क्षेत्रफळ आयनद्रायूमध्ये ठेवले असता, वरील क्रियेमुळे त्यावर ऋण भार जमा होऊन तेथे परिणामी ऋण विद्युत् दाब निर्माण होतो असे दिसेल. या गुणधर्मामुळे आयनद्रायू व साधा निर्विद्युत् वायू यांच्यातला भेद दाखवता येतो.

---

आयनद्रायू निर्मिती : प्रयोगशाळेत आयनद्रायू निर्माण करण्याच्या अनेक रीती आहेत पैकी दोन पद्धती पुढे दिल्या आहेत :

(अ) विद्युत् विसर्जन : कमी दाबाचा कोणताही वायू असलेल्या नलिकेवर विद्युत् अग्रांच्याद्वारे विद्युत् दाब लावला असता त्यामधून विद्युत् प्रवाह जाऊ शकतो. या पद्धतीत ऋणाग्र किंवा नलिकेतील वायू या दोहोंचे तपमान जास्त नसते. विद्युत् प्रवाह जात असताना नलिकेतील अग्रांच्या दरम्यान विद्युत् क्षेत्राचे वाटप कसे होते हे आ. १ मध्ये दाखवले आहे.

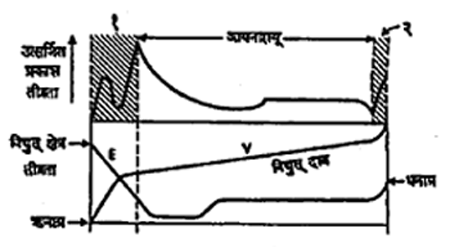
विभाग १, २ ही दोन विद्युत् भार आवरणे आहेत. यांच्यामधील विभागात आयनद्रायू तयार होतो. यात आयनीकरणाचे प्रमाण किंचित असते व सर्वसाधारणपणे हा आयनद्रायू क्रियाशील असतो T_{e &gt&gt} T_g.

(आ) वलयाकृती एकदिक् विद्युत् विसर्जन : ज्यावर विद्युत दाब दिला आहे अशा योग्य धातूच्या कांड्या हवेत प्रथम अगदी जवळ आणून नंतर त्या थोड्या दूर केल्या, तर हवेत एक तेज:पुंज असे विद्युत् विसर्जन दिसते. या प्रकारामध्ये अग्राचे (विशेषत:ऋणाग्राचे) व वायूचे तपमान खूप (म्हणजे काही हजार अंश के.) असते व त्यामध्ये आयन घनतेचे प्रमाण १०^१२ ते १०^१६ इतके सहज वाढू शकते. या विसर्जनामध्ये दोन्ही अग्रांजवळ विद्युत्°भार आवरणे सूक्ष्म असल्यामुळे, डोळ्यांना दिसणारा वक्राकार विसर्जनाचा भाग आयनद्रायूच असतो.

वरील पद्धतींचे समालोचन केल्यास असे आढळून येईल की, आयनद्रायू निर्मिर्तीचा प्राथमिक टप्पा म्हणजे वायूंचे आयनीकरण करणे हा आहे. हे साध्य करण्याकरिता वायूत जे काही थोडे इलेक्ट्रॉन असतात त्यांना लावलेल्या विद्युत् दाबामुळे ऊर्जा मिळते व त्यामुळे ते आघाताद्वारे वायूच्या अणूंचे आयनीकरण करतात. प्रचंड विद्युत् प्रवाह वायूमध्ये सोडून वायूचे तपमान कित्येक सहस्र अंशांपर्यंत वाढवले, तर वायूचे अणूसुद्धा या आघातांद्वारे आयनीकरणाच्या क्रियेला हातभार लावू शकतात. अशा परिस्थितीत, मेघनाद साहा यांनी गणिताद्वारे खालील समीकरणात दाखविल्याप्रमाणे त्या वायूत आयनीकरणाचे प्रमाण वाढत जाते.

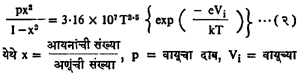
अणूंच्या आयनांत विदलन करण्याकरिता आवश्यक असलेला विद्युत् दाब (व्होल्टमध्ये), T = वायूचे तपमान, k = बोल्टस्‌मान स्थिरांक, e = इलेक्ट्रॉनावरील विद्युत् भार, exp हा नैसर्गिक लॉगरिथमाच्या पायाचा संक्षेप असून त्यापुढील कंस त्याचा घातांक समजावा, एक वातावरीणीय दाब असलेल्या पाऱ्याच्या वाफेचे तपमान ६,०००^० के. पर्यंत वाढवले तर x ≈ ^१/१००० असे साहा यांच्या वरील समीकरणावरून दाखवता येते. पूर्ण आयनीकरण करण्यास वायूचे तपमान केवढ्या प्रचंड प्रमाणात वाढविले पाहिजे याची कल्पना येते. अशा प्रकारचे तपमान अणुबाँबमध्ये अणुकेंद्रीय विक्रियेमुळे निर्माण होते. प्रयोगशाळेत ह्याच्या बरेचसे जवळचे तपमान प्रचंड विद्युत् प्रवाह सोडून निर्माण करता येते. असा अतिशय जास्त तपमानाचा आयनद्रायू निर्माण करण्यामध्ये अनेक तांत्रिक अडचणी आहेत. या तपमानाचा आयनद्रायू जर काचनलिकेत निर्माण केला व त्याच्या उष्णतेचा थोडा जरी भाग काचेच्या भिंतींपर्यंत पोचला तरी त्या वितळून त्यांची वाफ होईल. तथापि अशा आयनद्रायूमध्ये असलेल्या प्रचंड चुंबकीय क्षेत्रामुळे आयनद्रायू धारक भिंतीपासून दूर सरून आतील बाजूस आकुंचन पावतो. आयनद्रायू व धारक यांमध्ये जी पोकळी निर्माण होते ती उष्णतावाहक नसते.

चुंबकीय क्षेत्रजन्य साठवण : कोणत्याही नलिकेत जर वायू भरला, तर तो सर्वत्र सारखा पसरून ती नलिका पूर्णपणे भरून तिचा आकार धारण 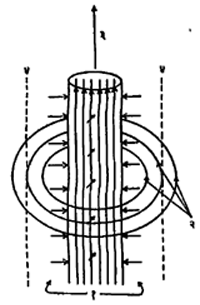करतो, हा वायूचा गुणधर्म सर्वांना माहीत आहे. नलिकेमध्ये जर आयनद्रायू असेल, तर भिंतीच्याजवळ सगळ्या बाजूस डेबाय-आवरण-लांबी एवढे एक विद्युत् भार वलय आयनद्रायू व भिंत यांमध्ये तयार होते. आयनद्रायूमध्ये वाहत असणारा विद्युत् प्रवाह जास्त प्रमाणाचा असेल, तर त्यायोगे निर्माण होणाऱ्या वर्तुळाकार चुंबकीय क्षेत्राचा आयनद्रायूवर परिणाम होऊन तो भिंतीपासून आकुंचन पावतो. या परिणामास स्वनिर्मित चुंबकीय आकुंचन म्हणतात. हे आकुंचन कसे होते हे आ. २ मध्ये स्पष्ट केले आहे.

आ. २ मध्ये दाखविल्याप्रमाणे आयनद्रायूत वाहणारा विद्युत् प्रवाह एका दिशेने वाहणाऱ्या अनेक समांतर विद्युत् प्रवाह घटकरेषांचा बनला आहे असे मानले, तर या घटकरेषा एकमेकांकडे आकर्षित होऊन आकुंचन पावतील, हे उघड आहे. या प्रश्नाचा अधिक खोल अभ्यास केल्यास दंडगोल आकाराच्या आयनद्रायूच्या बाह्य पृष्ठभागावर  या मूल्याचा एक अंतर्मुख दाब निर्माण होतो असे दाखवता येते. येथे I_o = आयनद्रायूमधील सपूर्ण विद्युत् प्रवाह, a = दंडगोल आयनद्रायूची त्रिज्या. बरील सूत्रात आयनद्रायूचे पूर्ण आयनीकरण झाले आहे व तो औष्णिक आयनद्रायू आहे, असे गृहीत धरले आहे. धारक भिंतीपासून आयनद्रायू अलग होऊन आसाकडे आकुंचन पावण्याकरिता 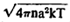एवढा किमान विद्युत् प्रवाह असणे आवश्यक आहे, असे दाखवता येते.

---

वर दिलेले समीकरण बेनेटे यांनी सैद्धांतिक विवेचनावरून काढले व त्यास बेनेट समीकरण असे म्हणतात. प्रयोगशाळेत आकुंचन परिणाम मात्र कझिन्स आणि वेअर यांनी १९५९ साली दाखवला. प्रयोगात असे दिसले की, अपेक्षित असे स्थिर आकुंचन न होता आकुंचनप्रसरण अशा क्रिया एकमेकांमागून अशा जलद होत जातात की, त्यामुळे शेवटी आयनद्रायू भिंतीवर आपटून नाश पावतो. प्रयोगशाळेत अति-उष्ण आयनद्रायू निर्माण केल्यानंतर त्याची साठवण चुंबकीय क्षेत्राद्वारा करणे आवश्यक आहे. स्वनिर्मित चुंबकीय क्षेत्रामुळे काही परिस्थितीत साठवण होते हे खरे, पण ती स्थिर नसते. त्यामुळे बाहेरून चुंबकीय क्षेत्र लावून ती स्थिर करण्याचे प्रयत्न (दोन प्रकारे) सध्या चालू आहेत.

(अ) स्टेलेरेटर योजना (श्पिट्सर तत्त्व) : वायू नलिकेत असणाऱ्या आयनाद्रायूवर जर त्या नलिकेच्या लांबीला समांतर असे एक तीव्र चुंबकीय

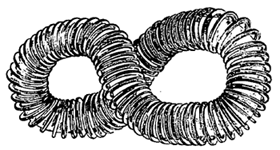
क्षेत्र निर्माण केले, तर त्यामुळे आयनद्रायू आकुंचन पावून भिंतीपासून अलग होतो असे आढळते. या योजनेत आयनद्रायू नलिका सरळ नसून (पहा : आ. ३) तिला इंग्रजी 8 या आकड्याचा आकार दिलेला असतो व तिच्याभोवती चुंबकीय क्षेत्र निर्माण करणारी वेटोळी या आकाराला अनुरूप अशी असतात.

(आ) चुंबकीय दर्पण योजना : या पद्धतीत आयनद्रायू नळीवर त्यातील विद्युत् प्रवाहाच्या दिशेला समांतर असे चुंबकीय क्षेत्र आ. ४ मध्ये दाखविल्याप्रमाणे अ आणि आ या ठिकाणी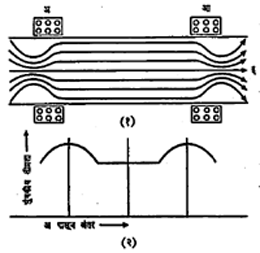 असलेल्या दोन वेटोळ्यांच्याद्वारे निर्माण केले जाते. मात्र या योजनेत चुंबकीय क्षेत्राची तीव्रता सारखी नसून ती आकृतीमध्ये दाखविलेल्या आलेखाप्रमाणे कमीजास्त होत असते. आता अ या ठिकाणी v  वेग असलेला धन (अथवा ऋण) आयन नळीच्या अक्षाशी θ^० कोन करून जर प्रवेश करीत गेला तर त्याचा मार्ग चुंबकीय क्षेत्रामुळे विचलित होतो. गतिमान आयनाच्या दृष्टिने क्षेत्राची तीव्रता कालाप्रमाणे बदलत असल्यामुळे विद्युत् चुंबकीय प्रवर्तन (संवाहकातील चुंबकीय क्षेत्र बदलत असताना त्यात विद्युत् दाब निर्माण होणे) नियमानुसार एक निराळ्याच प्रकारची प्रेरणा त्यावर कार्य करू लागते. या सर्व परिणामामुळे हे आयन भिंतीपासून दूर ठेवले जातातच पण त्यातील काही आयन अ आ या अवकाशाबाहेरसुद्धा जाऊ शकत नाहीत. चुंबकीय क्षेत्राच्या तीव्रतेत स्थानिक वाढ झाल्यामुळे त्याकडे येणारे आयनांचे परत परत परावर्तन होते. या क्रियेचे जास्त सविस्तर विवेचन पुढे केले आहे.

आयनद्रायूमधील आयनांची गतिकी : चुंबकीय व विद्युत् क्षेत्रे ही एकाच वेळी कार्य करीत असता आयनद्रायूच्या होणाऱ्या प्रतिक्रियेविषयी सूक्ष्म व सखोल ज्ञान करून घेण्याकरता प्रत्येक आयनाच्या गतीबद्दल माहिती करून घेणे आवश्क आहे.

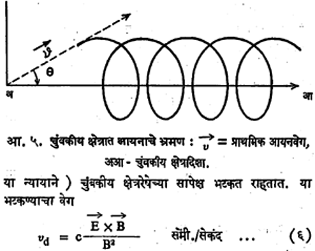
आयनांचे चुंबकीय क्षेत्रातील विचलन : आ. ५ मध्ये दाखविल्याप्रमाणे आयनद्रायू अ या ठिकाणी चुंबकीय क्षेत्राची दिशा अआ व तीव्रता B आहे व या ठिकाणी प्राथमिक वेग v असलेला एक धन आयन क्षेत्र दिशेशी Φ^० कोन करून चालला आहे, असे समजू. आयनाच्या क्षेत्राच्या दिशेतील वेगघटक v cosΦ व त्याच्या लंब दिशेतील वेगघटक v sinΦ आहेत. चुंबकीय क्षेत्रामुळे आयनाचा गतिमार्ग बदलून तो आकृतीत दाखविल्याप्रमाणे वेटोळ्याच्या आकाराचा होतो. क्षेत्राच्या दिशेने असणारा वेगघटक अचल राहतो, म्हणजे या दिशेने आयन एकाच स्थिर वेगाने मार्गक्रमण करीत राहतो दुसऱ्या घटकामुळे त्याला परिभ्रमण गती मिळून तो क्षेत्रदिशेभोवती फेऱ्या घालू लागतो व त्याचा परिणामी गतिमार्ग हा स्क्रूवरील आट्याप्रमाणे दिसतो. परिभ्रमण गतीचा कोनीय वेग ω_ci खालील सूत्राने मिळतो :

आ. ४. (१) चुंबकीय दर्पण योजना (अ, आ) चुंबकीय क्षेत्र निर्माण करणारी वेटोळी, (इ) आयन गतिमार्ग. (२) चुंबकीय क्षेत्र तीव्रता आलेख.

येथे v1 = v sin Φ, r = गोलाकार गतिमार्गाची त्रिज्या, B = क्षेत्राची तीव्रता, M = आयनाचे वस्तुमान, e = इलेक्ट्रॉनावरील विद्युत् भार (विद्युत स्थितिक एककात) व c = प्रकाशवेग. वरील सूत्राप्रमाणे हा वेग कायम व स्थिर राहतो. ω_ci हा आयनांच्या गतीचा एक महत्त्वाचा स्थिरांक आहे म्हणून त्यास आयन सायक्लोट्रॉन कोनीय कंप्रता (दर सेकंदास होणारी आवर्तने X 2π) असे म्हणतात. या स्थिरांकाची किंमत इलेक्ट्रॉनाकरिता निराळी व पुष्कळच जास्त असते. आतापर्यंत धन आयनावरील विद्युत् भार +e धरला आहे पण जर आयनद्रायूमध्ये अधिक विद्युत् भार असलेले धन आयन असतील, तर त्यावरील विद्युत् भार +Ze (Z म्हणजे अणुकेंद्रातील प्रोटॉनांची संख्या) असा मांडून जेथे सूत्रात e येत असेल तेथे Ze ही संख्या घातली असता त्या आयनाकरिता लागणारे सूत्र मिळेल. इलेक्ट्रॉनाकरिता e च्या ऐवजी -e आणि M च्या ऐवजी m घातले असता त्याचे सूत्र मिळते.

आयनद्रायूवर एकाच वेळी E तीव्रतेचे विद्युत् क्षेत्र व B तीव्रतेचे चुंबकीय क्षेत्र कार्य करीत असतील, तर त्यातील कोणत्याही एका आयनाची गती

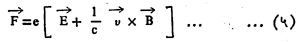
या समीकरणाने मिळते. या सूत्रात v हा त्या आयनाचा तात्कालिक वेग दाखवतो व F ही प्रेरणा आहे. या समीकरणात उजव्या बाजूकडील पहिले

पद आयन व विद्युत् क्षेत्र यांच्या परस्परक्रियेमुळे निर्माण होणारी प्रेरणा होय. ही प्रेरणा आयन व ते क्षेत्र यांच्यात असणार्‍या सापेक्ष गतीवर अवलंबून राहत नाही. सूत्रानुसार गतिजन्य विद्युत् क्षेत्राचे परिमाण उजव्या बाजूकडील दुसरे पद दाखवते. वरील सूत्रात येणार्‍या E आणि B या तीव्रता, बाहेरून लावलेली क्षेत्रे व आयनद्रायूमध्ये निर्माण होणारी क्षेत्रे या दोन्हींमुळे ठरल्या जातात. B या तीव्रतेत अवकाशानुक्रमे व कालानुक्रमे होणारा बदल मर्यादित असेल, तर वरील समीकरण सोडवून तिचे उत्तर काढणे सोपे आहे व त्यापासून पुढील निष्कर्ष काढता येतात : (अ) आयनाची परिभ्रमण गती कोणत्याही क्षणी एका केंद्राभोवती होते, असे मानून आयनाच्या गतीचे वर्णन या मार्गदर्शक केंद्राच्या आधारे करणे अगदी सुलभ होते. (आ) ही मार्गदर्शक केंद्रे (प्रत्येक आयनाला एक मार्गदर्शक केंद्र या न्यायाने) चुंबकीय क्षेत्ररेषेच्या सापेक्ष भटकत राहतात. या भटकण्याचा वेग

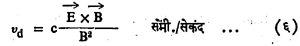 या सूत्राने मिळतो. (इ) या गतीमध्ये काही विशिष्ट राशी अचल राहतात. या राशींना अक्रमी अचल राशी म्हणतात.

भटकण्याचा वेग : सूत्र (६) वरून असे दिसते की, जर आयनद्रायूमधील विद्युत् क्षेत्राला व आयनाच्या प्राथमिक गतीला B च्या लंबाच्या दिशेने जर घटक असेल, तर दोन्ही गोष्टींचा परिणाम म्हणून आयनद्रायूला v_d हा भटकण्याचा वेग मिळतो. या वेगाची दिशा, B ची दिशा व विद्युत् क्षेत्राची दिशा या दोघांशी काटकोन करते. त्याची किंमत त्या आयनाचा विद्युत् भार, वस्तुमान किंवा प्राथमिक वेग यांपैकी कोणत्याही राशीवर अवलंबून असत नाही. ज्या संदर्भ-अक्ष-व्यूहाच्या सापेक्ष आयनद्रायूला v हा वेग आहे असे आढळते, त्याऐवजी त्याच गतीने व त्याच दिशेने जाणारे संदर्भ अक्ष मानले, तर 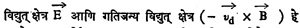एकमेकाला नाहीसे करतात व आयनाची गती परत वेटोळ्याच्या आकाराची होते असे दिसून येते. हा निष्कर्ष महत्त्वाचा आहे व तो पुढीलप्रमाणे मांडता येईल : विद्युत् क्षेत्राला कोणत्याही ठिकाणी जर चुंबकीय क्षेत्राच्या लंबाच्या दिशेत घटक असेल, तर त्यामुळे आयनद्रायूला अशी एक स्थानिक गती येते की, त्यामुळे

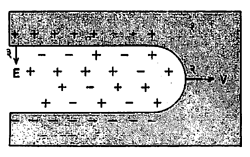
आयनद्रायूच्या स्वतःच्या संदर्भ-अक्षांना परिणामी विद्युत् क्षेत्र शून्य आहे, असे आढळून येते. या विधानाचे स्वरूप खालील उदाहरणावरून जास्त स्पष्ट होते. आ. ६ मध्ये आयनद्रायूची एक शलाका एका निर्वात अवकाशात v या वेगाने B तीव्रतेच्या चुंबकीय क्षेत्राच्या (१) लंब दिशेने प्रगत होत आहे. आयनद्रायूमधील आयनांच्या वाटपात फरक होऊन (३) या दिशेने दाखविलेले विद्युत् क्षेत्र (E) निर्माण झाले तरीही ही गती त्यामुळे v या वेगानेच चालू राहील.

आ. ७ मध्ये एका चुंबकीय क्षेत्रात निमग्न असा दंडगोल आकाराचा आयनद्रायू दाखवला आहे. चुंबकीय क्षेत्राची तीव्रता सर्वत्र हळूहळू वाढवली, तर विद्युत् प्रवर्तन सिद्धांताप्रमाणे निर्माण होणाऱ्या विद्युत् क्षेत्राच्या रेषा चक्राकार असतील प्रवर्तित झालेले विद्युत् क्षेत्र E व पहिले चुंबकीय क्षेत्र यांमुळे आयनद्रायूला चोहोकडून (४) या केंद्राकडे दाबत नेणारी प्रेरणा निर्माण होईल. आयनद्रायू जर पूर्ण विद्युत् वाहक आहे असे मानले, तर प्रवर्तित विद्युत् प्रवाह अक्षय राहतील व त्यामुळे चुंबकीय क्षेत्राच्या वाढणाऱ्या प्रेरणारेषा आयनद्रायूमध्ये कधीच प्रवेश करू शकणार नाहीत, हे स्पष्ट आहे.

---

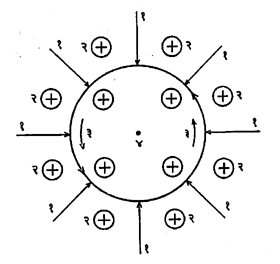
या उदाहरणावरून असे दिसते की, चुंबकीय क्षेत्रात साठवण केलेल्या आयनद्रायूत जर प्रवर्तन परिणाम किंवा विद्युत् भारशून्यता या स्थितींपासून विचलन, अशा कोणत्याही कारणाने जर विद्युत् क्षेत्र निर्माण झाले, तर त्यामुळे आयनद्रायूला ही भटकण्याची गती मिळते. या क्रिया अशा रीतीने परस्परावर अवलंबून राहतात की, अकस्मात निर्माण झालेली थोडीशी विचलन गती जोराने वाढत जाऊन आयनद्रायूला अस्थिर करते.

आयनद्रायू गतीच्या अक्रमी अचल राशी : एका मर्यादित आकारमानाच्या आयनद्रायूत होणारे बदल इतक्या जलद रीतीने होतात की, त्यामुळे आयनद्रायू व त्याच्या भोवतालचे भौतिकीय संच (यंत्रणा) यांमध्ये ऊर्जेची फारच थोडी देवघेव होते म्हणून अशा बदलांना अक्रमी बदल असे म्हणतात. अशा बदलांत आयनद्रायूच्या काही राशी अचल राहतात असे आढळते. अशा राशींचे सर्वात सोपे उदाहरण म्हणजे आयनांच्या चुंबकीय क्षेत्रात होणाऱ्या परिभ्रमण गतीमुळे निर्माण होणाऱ्या μ [चुंबकीय परिबल, à चुंबकत्व] या चुंबकीय राशीचे. वर्तुळाकार कक्षेत फिरणारा आयन व त्याच आकाराच्या तारेत वाहणारा विद्युत् प्रवाह यांचे परिणाम सारखेच असतात, असे दाखवता येते. त्यामुळे चुंबकीय क्षेत्र लावले असता या प्रवर्तित चुंबकत्वाची दिशा लेंट्स यांच्या नियमाप्रमाणे चुंबकीय क्षेत्राच्या विरुद्ध दिशेची होते. आयनावर कार्य करीत असलेल्या चुंबकीय क्षेत्रामधील होणारे बदल मर्यादित स्वरूपाचे असतील, तर आयनाच्या चुंबकीय राशीचे मान μ अचल राहील. वरील विवेचनात आयन आघात-क्रियेत भाग घेत नाही, असे गृहीत धरले आहे. या विवेचनानुसार चुंबकीय दर्पण योजनेत आयनांचे परावर्तन कसे होते, याची मीमांसा करता येते. समजा, जर आयनद्रायूतील एक आयन क्ष या ठिकाणाहून (चुंबकीय क्षेत्र तीव्रता B₁) तो य या ठिकाणी (चुं. क्षे. ती. B₂) जातो μ च्या अचलत्वामुळे 

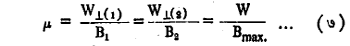
जर B₂ &gt B₁ असेल, तर तितक्याच प्रमाणात W_^(2) &gtW_^(1) होणे अनिवार्य ठरते. W_^ हा त्या आयनाच्या संपूर्ण ऊर्जेचा म्हणजे W चा एक भाग आहे. त्यामुळे जशी चुंबकीय क्षेत्राची तीव्रता वाढते त्याच प्रमाणात एकंदर ऊर्जेचा वाढता भाग W^ या भागात रूपांतरित केला जातो. त्यामुळे तिसऱ्या पदात दिलेल्या कमाल मर्यादेपर्यंत चुंबकीय क्षेत्राची वाढ झाली, तर त्यापुढे W^ मध्ये वाढ होऊ शकणार नाही व त्यामुळे जेथे क्षेत्राची तीव्रता यापेक्षा जास्त आहे त्या ठिकाणाहून आयनाचे पूर्ण परावर्तन होते. पण

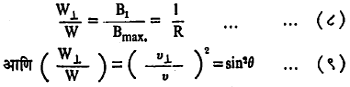
वरील सूत्रात R या राशीला परावर्तन गुणोत्तर म्हणतात. वरील समीकरणावरून असे दिसते की ज्याचा sin²θ≤ 1/R असेल, तो आयन परावर्तित होईल पण ज्याचा sin²θ &gt 1/R असेल, तो आयन चुंबकीय क्षेत्रात प्रवेश करील व त्याचा मार्ग वेटोळ्याच्या आकाराचा होईल. या सर्वांचा परिणाम असा होईल की, ठराविक संख्येचे आयन क्षय या अवकाशात अडकले जातील. या आयनांचे आघात होऊन त्यांची गतिदिशा योग्य रीतीने बदलली, तरच त्यांची या अवकाश सापळ्यातून सुटका होऊ शकेल. तीव्र तपमान असलेल्या आयनद्रायूमध्ये असे घडण्याची शक्यता फार असत नाही. याच तत्त्वाच्या उपयोगाचे दुसरे उदाहरण म्हणजे आयनद्रायूवर कार्य करीत असलेल्या चुंबकीय क्षेत्राच्या तीव्रतेत वाढ केली असता त्याचे होणारे आकुंचन हे होय. चुंबकीय क्षेत्र वाढवले असता त्याची त्रिज्या कमी होऊन त्याचे परिणामी अक्रमी आकुंचन होते असे दिसते. कोणत्याही वायूचे अक्रमी आकुंचन केल्यास त्याचे तपमान वाढते हे सर्वश्रुतच आहे. अशा रीतीनेसुद्धा आयनद्रायूचे तपमान वाढविता येते. आयनद्रायू हा पूर्ण विद्युत् वाहक आहे असे मानले, तर त्याच्या विभागाशी संलग्न असणारी चुंबकीय प्रेरणारेषांची संख्या ही अचल असते. समजा, एखाद्या आयनद्रायू विभागाशी संलग्न रेषासंख्या AB आहे. बाहेरून चुंबकीय क्षेत्र लावून ही संख्या बदलण्याचा प्रयत्न केला, तर प्रवर्तित विद्युत् प्रवाह सिद्धांताप्रमाणे आयनद्रायूमुध्ये असा विद्युत् प्रवाह निर्माण होतो की, जो विरुद्ध दिशेचे चुंबकीय क्षेत्र निर्माण करून या बदलाला विरोध करतो. यामुळे क्षेत्ररेषांची ही वाढ त्यामध्ये प्रवेश करू शकत नाही, म्हणजे या विभागातील प्राथमिक प्रेरणा रेषांची संख्या कायम राहील.

आयनद्रायूमधील आंदोलने : (क) इलेक्ट्रॉन आंदोलन : आयनद्रायूमध्ये अनेक प्रकारची स्थिर आंदोलने आढळून येतात. त्यांच्यात सर्वांत आकलन करण्यास सोपे म्हणजे लँगम्यूर व टाँक्स यांनी संशोधलेले इलेक्ट्रॉन आंदोलन हे होय. या आंदोलनाचे क्रियावर्णन करण्याकरिता प्रथम त्यांनी प्लाझ्मा (आयनद्रायू) ही संज्ञा उपयोगात आणली. ही आंदोलने, वायूमध्ये ज्या प्रकाराने ध्वनितंरग निर्माण होतात, त्यासारखीच बरीचशी आहेत. आयनद्रायूमध्ये विद्युत् भारशून्यता जोपर्यंत अस्तित्वात आहे तोपर्यंत आयनद्रायूमध्ये विद्युत् क्षेत्र कोठेही निर्माण होत नाही. पण काही कारणामुळे जर विद्युत् भारशून्यता स्थिती बदलून एका ठराविक भागात जास्त आयन राहिले (इलेक्ट्रॉन बाहेर गेल्यामुळे), तर तेथे एक असे विद्युत् क्षेत्र निर्माण होते की, जे ही विद्युत् भारशून्यता परत प्रस्थापित करू पाहते. याचा परिणाम असा होतो की, आयनद्रायूमध्ये इलेक्ट्रॉनांची आंदोलने उत्पन्न होतात. रूढ न्यूटन गतिकीचा वापर करून या आंदोलनांची कंप्रता (दर सेकंदास होणारी आंदोलनसंख्या) f_e ही

इतकी असते. एक तप्त ऋणाग्र असलेली नलिका घेऊन तिच्यात आर्‌गॉनासारखा वायू कमी दाबात भरून तिच्यावर एकदिक् विद्युत् दाब लावला असता, काही परिस्थितीत वाहणाऱ्या विद्युत् प्रवाहाचा काही अंश प्रत्यावर्ती (उलटसुलट दिशेने वाहणारा) होतो, यावरून या आंदोलनांचे अस्तित्व कळून येते. वरील विवेचनात इलेक्ट्रॉनांची आंदोलने इतकी जलद होतात की, त्यामुळे आयन जवळजवळ स्थिर राहतात, असे मानले आहे. विवेचनावरून ही आंदोलने स्थिर स्वरूपाची असतात व त्यामुळे आंदोलनतरंग आयनद्रायूमध्ये प्रगत होत नाहीत, असे दिसून येते. औष्णिक हालचाल जर विचारात घेतली, तर हे तरंग प्रगत स्वरूपाचे होतात, असे नंतरच्या संशोधनावरून कळून आले.

(ख) आयन आंदोलने : वरील प्रकारची आंदोलनक्रिया आयनांच्या बाबतीतसुद्धा होऊ शकते. ही आंदोलने इतकी संथपणे होतात की, आयनद्रायूमधील इलेक्ट्रॉनांच्या गतिवितरणाला त्या अवधीत

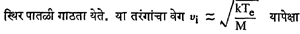
जास्त नसतो. येथे T_e = इलेक्ट्रॉनांचे तपमान, M = आयनाचे वस्तुमान व k = बोल्टस्‌मान स्थिरांक. आयन आंदोलनांची कंप्रता काही किलोहर्ट्‌झच्या आसपास आढळते.

(ग) गतिमान पुंजके : आणखी एका निराळ्या प्रकारची आंदोलने काही परिस्थितीत आढळतात. जेव्हा आयनद्रायूचा सर्वत्र असलेला सारखेपणा नष्ट होतो तेव्हा त्यांच्यात पुंजके निर्माण होतात व ते गतिमान होऊन आयनद्रायूमध्ये आवर्त (ठराविक कालानंतर पुन्हा पुन्हा) क्षोभ निर्माण करतात. या निरनिराळ्या क्षोभांवरील संशोधनावरून असे दिसते की, अशा प्रकारची आंदोलने सर्वसाधारणपणे आयनद्रायूमध्ये नेहमीच आढळतात व त्यामुळे असे क्षोभ आयनीकृत वायूचा एक गुणधर्म आहे असे म्हणावयास हरकत नाही.

(घ) आल्फव्हेन तरंग : आयनीकृत वायू माध्यमावर जर स्थिर चुंबकीय क्षेत्र कार्य करीत असेल, तर त्याच्यात चुंबकीय द्रवगतिकीप्रमाणे एक निराळ्याच प्रकारचे तरंग प्रगत होऊ शकतात. हे तरंग अवतरंग (ज्यातून तरंग जातात त्या माध्यमाचे बिंदू वेगदिशेशी काटकोनात स्थलांतरित होतात ते तरंग) असून त्यांचा वेग

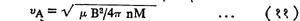
एवढा असतो. यात B = चुंबकीय क्षेत्र, M = आयनाचे वस्तुमान, n = आयन आयतन घनता व μ = माध्यमाची चुंबकीय पार्यता. या तरंगांच्या प्रसारणामध्ये आयनच भाग घेत असल्यामुळे जेव्हा या तरंगांची कंप्रता आयन सायक्लोट्रॉन कंप्रतेएवढी होते, तेव्हा अनुस्पंदन होऊन त्या तरंगांचे आयनद्रायूमध्ये अपस्करण (कंप्रतेनुसार विभागणी) होऊ लागते.

(च) विद्युत् चुंबकीय तरंग : इतर कोणत्याही माध्यमाप्रमाणे आयनद्रायूमध्येसुद्धा प्रसारण पावणारे विद्युत् चुंबकीय तरंग निर्माण करता येतात. तरंगांची कोनीय कंप्रता ω ही जर इलेक्ट्रॉन आयनद्रायू कंप्रता ω_p पेक्षा कमी असेल, तर आयनद्रायू अशा तरंगांकरिता अपारदर्शक असतो. ω &gt ω_p असली म्हणजे आयनद्रायू पारदर्शक होऊन तो, ज्याचा प्रणमनांक [विद्यूत् चुंबकीय तरंग एका माध्यमातून दुसर्‍या माध्यमात जात असताना होणार्‍या दिशाबदलासंबधीचे

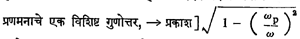
आहे अशा माध्यमासारखा वागतो. आयनद्रायूमध्ये प्रवेश करणार्‍या विद्युत् चुंबकीय तरंगांची कोनीय कंप्रता ω ही ω_p पेक्षा जास्त असेल, तरच ते तरंग आयनद्रायूमधून पुढे जाऊ शकतात. यापेक्षा कमी कंप्रतेच्या तरंगांकरिता आयनद्रायू हा अपारदर्शक असल्यामुळे त्यांचे पूर्णपणे परावर्तन होते. या 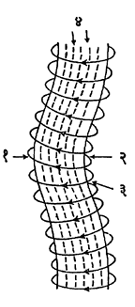गुणधर्माचा एक मोठा महत्त्वाचा उपयोग व्यवहारात होतो. पृथ्वीभोवती काही किलोमीटर उंचीवर सर्वत्र ω_p चे विशिष्ट मूल्य असलेला आयनद्रायू आहे. रेडिओ प्रेषकाने प्रेषित केलेल्या तरंगाची कंप्रता या ω_p च्या किंमतीपेक्षा कमी असेल, तर हे तरंग आयनद्रायूमध्ये पूर्णपणे परावर्तित होऊन ते पृथ्वीकडे परत फेकले जातात. एखाद्या स्थानकापासून प्रेषित केलेले असे तरंग परावर्तित होऊन दुसर्‍या स्थानकापर्यंत पोहोचू शकतात. हा परिणाम जर न होता, तर हे तरंग पृथ्वीच्या पृष्टभागाच्या वक्रतेमुळे त्या दुसर्‍या ठिकाणी कोणत्याही परिस्थितीत पोहोचू शकले नसते. याउलट पृथ्वीबाहेर दूर असलेल्या (उदा., चंद्र) वस्तूशी जर रेडिओ दळणवळण साधावयाचे असेल, तर त्याकरिता तरंगांची कंप्रता ω_p पेक्षा जास्त असली पाहिजे हे स्पष्ट आहे       [→ आयनांबर].

आयनद्रायूमधूल अस्थैर्य : आयनद्रायूमधील अस्थैर्य हे मुख्यत्त्वे करून दोन प्रकारचे असते. (अ) अवकाश अस्थैर्य, (आ) गतिक अस्थैर्य. पहिल्या प्रकाराचे महत्त्वाचे उदाहरण म्हणजे चुंबकीय क्षेत्रात वाहत जाण्याच्या गतीमुळे किंवा इतर कारणामुळे होणारे अस्थैर्य हे होय. स्वनिर्मित चुंबकीय क्षेत्रात असलेल्या आयनद्रायूमध्ये सर्वसाधारणपणे आढळणारे दोन परिणाम आ. ८ व आ. ९ मध्ये दाखविले आहेत.

आयनद्रायूमध्ये जर काही कारणामुळे अकस्मात वक्रता निर्माण झाली, तर तिच्यामुळे होणार्‍या चुंबकीय क्षेत्राच्या प्रमाणामधील फरकामुळे मूळ विचलनाचे वर्धन होऊन समतोल भंग पावतो (आ. ९). आयनद्रायूमध्ये अकस्मात संकोच निर्माण झाला, तर त्याचे असेच वर्धन होऊन त्यात अस्थैर्य निर्माण होते.

---

गतिक अस्थैर्याचे उदाहरण आपणास द्रवगतीत नेहमी आढळते. रबराच्या नळीतून पाणी कमी वेगाने सोडले, तर ते संथपणे वाहते व त्याच्या गतिरेषा सरळ व समांतर असतात. याउलट जर पाण्याचा दाब वाढवून त्याचा वेग वाढवला, तर एका ठराविक मर्यादेनंतर त्याची गती अस्थिर होते असे आढळते. आयनद्रायूमधील विद्युत् प्रवाह वाढवला असता, अशा प्रकारची अस्थिरता काही परिस्थितीत निर्माण होते.

आयनद्रायूमधील कणांचे आघात प्रकार :आयनद्रायूमध्ये सर्वसाधारणपणे तीन घटक (अ) इलेक्ट्रॉन, (आ) धन आयन व (इ) निर्विद्युत् अणू असतात, हे मागे सांगितलेच आहे. या घटकांमध्ये परस्परक्रियेमुळे निरनिराळ्या प्रकारचे आघात होतात त्यामुळे दोन परिणाम होतात. (अ) त्या घटकांच्या गतिवितरणात समतोलता येते व हे वितरण मॅक्स्वेलबोल्टस्‌मान सांख्यिकीप्रमाणे मिळते [→ सांख्यिकीय भौतिकी]. (आ) काही आघातांमुळे प्रकाश व इतर विद्युत् चुंबकीय तरंगांचे उत्सर्जन होते. आयनद्रायूमध्ये प्रकाशाचे उत्सर्जन भरपूर होते याचा उल्लेख मागे आलाच आहे.

इलेक्ट्रॉन आघात: निर्विद्युत् अणूंसमवेत होणाऱ्या आघातांची वर्गवारी खालीलप्रमाणे करता येते. (प) स्थितिस्थापक : या तऱ्हेच्या आघातामध्ये भाग घेणाऱ्या दोन घटकांची एकूण गतिज ऊर्जा व संवेग (वस्तुमान × वेग) कायम राहतात आणि अणूंच्या अंतस्थ ऊर्जेमध्ये बदल होत नाही. इलेक्ट्रॉनांची गतिज ऊर्जा जास्त नसेल ( ** २ ते ३ इलेक्ट्रॉन व्होल्ट), तर त्या भागातील आघात स्थितिस्थापक असतात. लघू तपमान असलेल्या आयनद्रायूमध्येच या आघातांना महत्त्व आहे. तीव्र तपमान असलेल्या आयनद्रायूमध्ये अशा प्रकारचे आघात अल्प असतात. (फ) याउलट अस्थितिस्थापक आघातामध्ये अणूंच्या अंतस्थ ऊर्जेत बदल होऊन त्याच्यापासून ऊर्जेचे उत्सर्जन, आयनीकरण, विदलन किंवा जोडणी इ. होणाऱ्या क्रिया खालील समीकरणाने दाखवता येतात.

A + e− fast ® A*+ e− siow ® A + hn + e − slow            (१२)

इलेक्ट्रॉनांच्या आघातामुळे प्रथम अणू उद्दीपित (* अशी खूण) होतो व त्यानंतर थोडक्याच अवधीत तो आपोआप प्रकाशकणांचे उत्सर्जन करतो. येथे h व n म्हणजे प्लांक स्थिरांक व कंप्रता होय.

आयनीकरण :  A + e− fast®A⁺+ e− slow+ e− … (१३)

विदलन : A₂ + e− fast®A+A+ e− slow …   (१४)

येथे A₂ हा दोन A अणूंपासून बनलेला रेणू आहे.

जोडणी : A₂ +  e− ®A−

इलेक्ट्रॉन व धन आयन आघात :(भ) आयनांचा उत्सर्गयुक्त पुन:संयोग : e− + A⁺ ® A + hn…                           …   (१६)

या क्रियेमध्ये निर्विद्युतीकरणाची ऊर्जा व इलेक्ट्रॉनांची गतिज ऊर्जा उत्सर्जित केली जाते.

(म) विदलनांकित पुन:संयोग : e− + A₂® A + A (१७)

अशा प्रकारच्या विक्रियेची शक्यता (भ) या विक्रियेपेक्षा काही सहस्रपटींनी अधिक असते.

इलेक्ट्रॉन व क्षेत्र विक्रियेमुळे उत्सर्जन : (य) एखाद्या गतिमान इलेक्ट्रॉनाची गतिरेषा जेव्हा धन आयनाच्या विद्युत् क्षेत्रात खोलवर शिरते, तेव्हा इलेक्ट्रॉनाला मिळणाऱ्या तीव्र प्रवेगामुळे तो विद्युत् चुंबकीय प्रारणाचे उत्सर्जन करतो. या प्रारणास ब्रेम्सस्ट्राहलुंग ही संज्ञा आहे. (र) लावलेल्या चुंबकीय क्षेत्रात इलेक्ट्रॉन वर्तुळाकार कक्षेत फिरतो तेव्हा त्याला प्रवेग असतो व त्यामुळे तो सायक्लोट्रॉन कोनीय कंप्रतेचे तरंग उत्सर्जित करतो. बीटाट्रॉन या प्रवेगकात (अणूघटकांचा वेग वाढविण्याच्या साधनात) इलेक्ट्रॉनांना प्रवेग दिल्यावर त्यापासून निळ्या रंगाचा प्रकाश मिळत राहतो त्याचे हे कारण आहे असे समजले जाते. (ल) कक्षेत फिरत असलेल्या इलेक्ट्रॉनांचा वेग u हा प्रकाशवेगापेक्षा (c पेक्षा) बराच कमी असेल, तर वरील क्रियेमुळे निर्माण होणाऱ्या विसर्जनाला सायक्लोट्रॉन विसर्जन असे म्हणतात. जर इलेक्ट्रॉनांचा वेग c च्या जवळपास असेल, तर याच विसर्जनाला सिंक्रोट्रॉन विसर्जन म्हणतात.

आयनद्रायू प्रारण : उष्ण पदार्थापासून उष्णता ऊर्जेचे बहिर्गमन बहुतांशी उत्सर्जनाच्या स्वरूपात होते. संपूर्ण कृष्ण पदार्थापासून (सर्व विद्युत् चुंबकीय तरंगांचे शोषण करणाऱ्या आदर्श पदार्थापासून) जेवढे ऊर्जेचे उत्सर्जन होते, त्यापेक्षा कितीतरी कमी पटीने त्याच तपमानाच्या आयनद्रायूतून होते असे आढळते. त्यामुळे आयनद्रायूमधून उष्णता उत्सर्जन होण्याचे प्रकार फक्त दोनच राहतात : (१) ब्रेम्सस्ट्राहलुंग, (२) सायक्लोट्रॉन किंवा सिंक्रोट्रॉन उत्सर्जन.

आयनद्रायूची विद्युत् संवाहकता : आयनद्रायूमधील विद्युत् प्रवाहाचा फार मोठा भाग इलेक्ट्रॉन वाहून नेतात. किंचित आयनीकृत आयनद्रायूची विद्युत् संवाहकता (s) खालील सूत्राने मिळते :

s = 0.532	n	.	e2	.	l	… (१८)
	n		Ö`mkTe		Q

येथे n_o = निर्विद्युत् वायूच्याअणूंची घनफळ घनता, n = आयन घनफळ घनता, T_e = इलेक्ट्रॉनांचे तपमान, Q = अणूचा आघाताकरिता संपूर्ण काटछेद (लक्ष्य म्हणून उपलब्ध असलेले अणूचे परिणामी क्षेत्रफळ), m = इलेक्ट्रॉनाचे वस्तुमान व e = इलेक्ट्रॉनाचा विद्युत् भार. वरील सूत्रावरून इलेक्ट्रॉनांचे तपमान वाढवले असता विद्युत् संवाहकता कमी होते असे दिसेल. या सूत्रामध्ये इलेक्ट्रॉन व अणू यांमध्ये स्थितिस्थापक आघात होतात असे गृहीत धरले आहे.

वायूतील आयनांच्या संख्येत प्रचंड वाढ केली, तर इलेक्ट्रॉन व आयन यांमध्ये होणाऱ्या कुलंब प्रेरणेची (दोन विद्युत् भारांमध्ये कुलंब सूत्रान्वये निर्माण होणाऱ्या प्रेरणेची)  दखल द्यावी लागते. अशा

परिस्थितीत	n	» l,	Te	» l
	no		T

होऊन त्या आयनद्रायूचे औष्णिक आयनद्रायूत रूपांतर होते. अशा आयनद्रायूची विद्युत् संवाहकता श्पिट्सर सूत्राने मिळते, ती अशी :

s =	T ³/²	¼¼(१९)
	6.5 ´ 103| Ù

In Ù या राशीची किंमत n व T_e यांवर अवलंबून असून ती साधारणपणे ५ ते २४ च्या दरम्यान असते. या सूत्रावरून असे दिसते की, या प्रकारच्या आयनद्रायूचे तपमान वाढवले असता, त्याची विद्युत् संवाहकता वाढत जाते. दशलक्ष केल्व्हिन अंशांपर्यंत जर तपमान वाढवले तर अशा आयनद्रायूची विद्युत् संवाहकता जवळजवळ तांब्याच्या विद्युत् संवाहकतेएवढी होते. असा तीव्र तपमानाचा आयनद्रायू संपूर्ण विद्युत् संवाहक आहे असे का मानतात, याचे मर्म वरील विधानावरून कळते.

एकदिक् विद्युत् दाब लावला असता आयनद्रायूमधून किती विद्युत् प्रवाह जाईल हे वरील विद्युत् संवाहकतेवरून काढता येते. जर लावलेला विद्युत् दाब प्रत्यावर्ती असून त्याची कंप्रता अधिक असेल, तर आपणास ॲपलटन व चॅपमन यांनी विवेचन करून काढलेले खालील सूत्र वापरावे लागेल.

s =	w2 p	(	n	)-	Jw2 p	(	w	)	… (२०)
	4p		n2+w2		4p		n2+w2

वरील सूत्रात n = आघात कंप्रता, w = लावलेल्या विद्युत् दाबाची कोनीय कंप्रता, w_p = आयनद्रायूमधील इलेक्ट्रॉनांची कोनीय कंप्रता व  J = √-1 . या सूत्रावरून आयनद्रायू w&lt w_p करता का अपारदर्शक आहे व w&gt w_p असेल, तर तो का पारदर्शक होतो हे समजण्यास मदत होते.

संदर्भ : 1. Brown, S. C. Basic Data of Plasma Physics, New York, 1959.

2. Delcroix, L. L. Plasma Physics, New York,, 1965.

3. Spitzer, L. Physics of Fully Ionised Gases, New York, 1958.

4. Uman, M. A. Introduction to Plasma Physics, New York, 1964.

चिपळोणकर, व. त्रिं.

“