गणितीय उपकरणे : सामान्यतः गणितीय प्रश्न सोडविण्यासाठी ज्या उपकरणांची मदत होते त्यांना गणितीय उपकरणे म्हणतात. कोनमापक, पट्टी, कंपास इ. उपकरणे भौमितिक आकृत्या काढण्यासाठी उपयोगी पडतात. ⇨गोटीचौकट व ⇨गणकपट्टी ही उपकरणे प्राथमिक संख्यात्मक प्रश्न सोडविण्यास उपयुक्त आहेत. कोष्टके तयार करणारी, प्राथमिक संख्यात्मक प्रश्न टंकलिखित स्वरूपात सोडवून देणारी इ. विविध कार्यालयीन व व्यावसायिक कामांकरिता उपयोगी पडणारी अनेक साधने प्रचलित आहेत. निरनिराळ्या प्रकारच्या संगणकांच्या (गणकयंत्रांच्या) साहाय्याने अनेक गुंतागुंतीचे प्रश्न अतिशय जलद सोडविता येतात [→ आरेखन, अभियांत्रिकीय व्यावसायिक व कार्यालयीन उपकरणे संगणक]. वरील उपकरणांखेरीज सांत समीकरणे आणि ⇨अवकल समीकरणे सोडविणारी तसेच ⇨अवकलन व समाकलन ही गणितीय कृत्ये करणारी विविध उपकरणे प्रचारात आहेत व प्रस्तुत लेखात या उपकरणांचे विशेष वर्णन केलेले आहे. अमेरिकेच्या संयुक्त संस्थानांच्या नॅशनल रिसर्च कमिटीतर्फे प्रसिद्ध करण्यात येणाऱ्या मॅथेमॅटिकल टेबल्स अँड अदर एड्स टू कॉम्प्यूटेशन या त्रैमासिकात विविध नवीन गणितीय उपकरणांची माहिती देण्यात येते.
विज्ञानाच्या विविध शाखांतील आणि उद्योगधंद्यांतील अनेक प्रश्न (उदा., अवकाशात सोडलेल्या रॉकेटाचा मार्ग, विविध आकारांच्या व आकारमानांच्या नळ्यांतील निरनिराळ्या द्रवांचे प्रवाह इ.) गणितीय भाषेत मांडता येतात. यामुळे हे प्रश्न जलद रीतीने सोडविणारी व आर्थिक दृष्ट्या परवडणारी उपकरणे शोधण्यास व त्यांचे उत्पादन करण्यास मोठी चालना मिळाली. अशा उपकरणांत एखाद्या पट्टीवरील दोन खुणांतील अंतर, तारांमधील विद्युत् प्रवाह किंवा वर्चस् (विद्युत् स्थिती ), स्थितिस्थापक पटलावर पडणारा ताण यांच्यासारख्या मोजता येतील अशा भौतिक राशींच्या रूपात गणितीय राशींचे निदर्शन करण्यात येते. ज्या गणितीय संबंधांवरून एखादा प्रश्न सोडवावयाचा असेल त्यांची उपकरणाच्या अभिकल्पात (आराखड्यात) वापरण्यात येणाऱ्या भौतिकीय नियमांशी सांगड घालण्यात येते. ज्या भौतिक प्रश्नांचे उत्तर काढण्यासाठी गणितीय उपकरण तयार केलेले असते, त्या प्रश्नांचे ते उपकरण म्हणजे एका दृष्टीने सदृश रूपच असते. आंशिक अवकल समीकरणे सोडविणाऱ्या काही उपकरणांच्या बाबतीत ही सदृशता पुष्कळच जवळची असते.
सांत समीकरणे सोडविण्याची उपकरणे : ही उपकरणे बैजिक किंवा बीजातीत (बैजिक नसलेली, उदा., त्रिकोणमितीय) सांत समीकरणे सोडवितात. या उपकरणांत दिलेल्या चलांतील (बदलणाऱ्या राशींतील) संबंध प्रस्थापित करण्यासाठी ⇨ कॅम, शृंखला, बदलत्या विद्युत् राशी इ. वापरण्यात येतात.
भरती पूर्वसूचक : एखाद्या बंदरातील समुद्राच्या भरतीची उंची अजमावण्यासाठी किंवा तत्सम सरल हरात्मक गतींच्या (एक प्रकारच्या कंपनांच्या, अशा कंपनांत प्रवेग हा कंप पावणाऱ्या वस्तूच्या स्थिर स्थितीपासून होणाऱ्या स्थानांतरणाच्या प्रमाणात असतो) संयोगांचा परमप्रसर (स्थिर स्थितीपासून लंब दिशेने होणारे कमाल स्थानांतरण) काढण्यासाठी या उपकरणाचा उपयोग होतो. कोणत्याही बंदरातील भरतीची उंची ही कालाचे फलन (गणितीय संबंध) असून हे फलन कालाच्या अनेक सरल हरात्मक फलनांच्या बेरजेने मिळविता येते. या फलनांचे आवर्तकाल (ज्या किमान कालानंतर फलनाचे मूल्य तेच येते तो काल) सूर्य व चंद्र याच्या भासमान गतींशी जुळते असतात. अशा प्रकारे भरतीच्या उंचीचे त्रिकोणमितीय बेरजेने निदर्शन करता येते एकदा भरतीच्या विविध सरल हरात्मक घटकांचे परमप्रसर काढले म्हणजे एकूण उंची काढता येते. आकडेमोड टाळण्यासाठी लॉर्ड केल्व्हिन यांनी १८७२ मध्ये आठ त्रिकोणमितीय घटक निर्माण करण्यासाठी कमी जास्त लांबी करता येणाऱ्या आठ भुजांच्या टोकांवर बसविलेल्या आठ कप्प्यांचा उपयोग केलेला होता. एका लाकडी चोकटीच्या वर त्यांपैकी चार कप्प्या व खाली चार कप्प्या बसविलेल्या होत्या. एका टोकाशी घट्ट बांधलेली एक दोरी वरच्या कप्प्यांच्या वरील बाजूने आणि खालच्या कप्प्यांच्या खालच्या बाजूने क्रमाक्रमाने नेऊन तिच्या दुसऱ्या टोकाला एक वजन व एक दर्शक जोडलेला होता. प्रत्येक कप्पीच्या मध्याला उभा व आडवा सरल हरात्मक घटक असलेली वर्तुळाकार गती मिळते. या वर्तुळाची त्रिज्या वरच्या व खालच्या कप्प्यांतील अंतराच्या मानाने बरीच लहान असल्यास आडव्या घटकाचा परिणाम कमी असतो आणि मुख्य परिणाम उभ्या सरल हरात्मक घटकाचाच असतो. केल्व्हिन यांच्या या उपकरणासारखीच परंतु आडव्या गतीचे निर्मूलन करून अधिक घटक असलेली मोठी उपकरणे नंतर तयार करण्यात आली. १९१० मध्ये तयार करण्यात आलेल्या एका उपकरणात ३७ घटक असून त्यावर सात वर्षांच्या भरतीचे वक्र १२ तासांत काढता येतात.
हरात्मक संश्लेषक : काही भौतिकीय फलने, उदा., प्रत्यावर्ती (उलट सुलट दिशेने वाहणारा) प्रवाह जनित्राने निर्माण केलेला विद्युत् दाब, एकाच मूलभूत आवर्तकालाचे उपगुणक आहेत असे आवर्तकाल असलेल्या घटकांच्या बेरजेने निदर्शित करता येतात. बरेचसे हरात्मक संश्लेषक (दोन वा अधिक हरात्मक गतींचे संयोग करणारी उपकरणे) केल्व्हिन यांच्या भरती पूर्वसूचकाच्या धर्तीवरच परंतु घटक गतींचे आवर्तकाल एखाद्या मूलभूत आवर्तकालाचे उपगुणक असण्याच्या दृष्टीने कप्प्या बसविलेल्या अक्षांच्या वेगाचे गुणोत्तर १: २ : ३ इत्यादी राहील अशा प्रकारे सुधारणा केलेल्या स्वरूपाचे आहेत. कप्प्यांच्या विस्थापनांच्या बेरजेचा उपयोग करण्याऐवजी स्प्रिंगांच्या एका संचाने निर्माण केलेल्या प्रेरणांच्या बेरजेचा उपयोग करून मायकेलसन व स्ट्रॅटन यांनी एक वेगळ्या धर्तीचा हरात्मक संश्लेषक तयार केला. १८९७ साली २० घटकांचे एक उपकरण व १८९८ मध्ये ८० घटकांचे दुसरे उपकरण तयार करण्यात आले.
बहुपदी निर्वाहक : संदेशवहनाच्या विद्यूत् मंडलांचे अभिकल्प तयार करण्यासाठी तसेच गतिमान प्रणालीची स्थिरता निर्धारित करण्यासाठी
फ (झ) = अ० + अ१ झ + अ२ झ२ +………+ अप झप
अशा स्वरूपाची बहुपदी सोडवावी लागते. म्हणजे झ च्या कोणत्या मूल्यांकरिता फ (झ) = ० होईल हे शोधून काढावे लागते. याकरिता बहुपदी निर्वाहकाचा (बहुपदीचे उत्तर काढणाऱ्या उपकरणांचा) उपयोग होतो. बहुपदी सहगुणकांतील
क्ष = मअ १ ज्या (थ) + म २ अ २ ज्या (२ थ)
+ ….. + म प अ प ज्या (प थ)
य = अ ० + म अ १ कोज्या (थ) + म २ अ२ कोज्या (२ थ)
+ …… + म प अ प कोज्या (प थ)
या संबंधांवरून जात्य-सहनिर्देशक (एकमेकांना लंब असणाऱ्या अक्षांपासून बिंदूचे स्थान दर्शविणारे अंक) काढून जर वक्र आरेखित केला असेल आणि जर हा वक्र क्ष = ०, य = ० या बिंदूमधून र वेळा जात असेल तर दिलेल्या बहुपदीस र बीजे असतात. या बीजांची केवल मूल्ये म पेक्षा कमी असतात असे सदसत् चलांच्या सिद्धांतावरून दाखविता येते [→ फलन].
अशा तऱ्हेचे वक्र काढणारे यंत्र फ्राय व डीटत्सोल्ट यांनी १९३७ मध्ये तयार केले. यांत्रिक रचनेच्या दृष्टीने हे यंत्र दहा घटक असलेल्या केल्व्हिन प्रकारच्या हरात्मक संश्लेषकासारखेच आहे. या यंत्रात ‘ज्या’ घटकांची बेरीज करून एका पेन्सिलीच्या टोकाला गती देण्यासाठी त्यांचा उपयोग करतात. ‘कोज्या’ घटकांची स्वतंत्रपणे बेरीज करून त्यांच्याद्वारे एका टेबलास गती दिली जाईल अशी व्यवस्था केलेली असते. या दोन गतीच्या दिशा एकमेकांना काटकोन करतात. या यंत्राने सत् सहगुणक [→ संख्या] असलेल्या बहुपदी सोडविता येतात. लिरोय ब्राऊन यांनी स्वत: तयार केलेल्या हरात्मक संश्लेषक विश्लेषकाचा अशाच प्रकारे सदसत् सहगुणक असलेल्या बहुपदी सोडविण्यासाठी उपयोग केला.
हार्ट आणि ट्रॅव्हिस यांनी १९३७ साली विद्युतीय रीत्या संश्लेषण करणारा बहुपदी निर्वाहक तयार केला. या यंत्रात घटकांचे निदर्शन संयोजनक्षम रोहित्रांच्या (विद्युत् दाब बदलणाऱ्या साधनांच्या) एका संचाने निर्माण केलेल्या विद्युत् दाबांद्वारे केले जाते. रोहित्रांचे प्राथमिक विद्युत् दाब मप अपया सहगुणकांच्या प्रमाणात असतात. रोहित्रांच्या द्वितीयक गुंडाळ्या एकसरीत (एकापुढे एक) जोडून द्वितीयक विद्युत् दाबांची बेरीज करण्यात येते. प्रत्यक्ष उपकरण वापरताना ‘ज्या’ बेरीज आणि ‘कोज्या’ बेरीज दर्शविणारे विद्युत् दाब शून्य होतील अशा प्रकारे म आणि थ यांच्या मूल्यांचे संयोजन करण्यात येते. म आणि थ यांच्या ज्या मूल्यांकरिता शून्य बिंदू प्राप्त होईल त्या मूल्यांवरून झ = मथ हे बहुपदीचे एक बीज मिळते.
एकघाती बैजिक समीकरण निर्वाहक : सांख्यिकीय माहितीतील सहसंबंध (चलांमध्ये असणारा परस्पर संबंध), विद्युत् शक्तीचे वितरण करणाऱ्या जालकांतील विद्युत् प्रवाह, बांधकामाच्या संरचनेतील प्रतिबले (विकृती निर्माण करणाऱ्या प्रेरणा) यांच्यासारखे प्रश्न सोडविण्यासाठी खालील स्वरूपाच्या एकघाती बैजिक समीकरण प्रणालीचा निर्वाह (उत्तर) काढावा लागतो.
क०० + क०१ क्ष१ + क०२ क्ष२ + … … + क०प क्षप = ०
क१० + क११ क्ष१ + क१२ क्ष२ + … … + क१प क्षप = ०
… … … … … … … …
कप० + कप१ क्ष१ + कप२ क्ष२ … … + कपप क्षप = ०
यात कयर ही दिलेली संख्यात्मक मूल्ये असून या समीकरणांची पूर्तता करणारी क्षय ची मूल्ये काढावयाची असतात.
या प्रकारची उपकरणे तयार करण्यासाठी स्प्रिंगा किंवा वजने यांच्यामुळे निर्माण होणाऱ्या प्रेरणांचे संतुलन किंवा एकमेकांना जोडलेल्या भांड्यातील द्रवाने गाठलेली पातळी यांसारख्या प्रयुक्त्यांचा उपयोग केला जातो. या उपकरणांमु्ळे मिळणारी अचूकता सामान्यतः कमी असल्याने व दिलेल्या प्रश्नाच्या माहितीनुसार उपकरणाचे संयोजन करण्यास फार वेळ लागत असल्याने या उपकरणाचा फारसा प्रसार झालेला नाही.
एकघाती समीकरणांची प्रणाली सोडविण्यासाठी मॅलॉक यांनी १९३३ मध्ये एका विद्युत् उपकरणाचे वर्णन केले होते. या उपकरणात प्रत्येक अज्ञात चलासाठी एक रोहित्र व प्रत्येक समीकरणासाठी एक बंद विद्युत् मंडल वापरण्यात येते. सहगुणकांसाठी प्रत्येक रोहित्राच्या गाभ्याभोवतील प्रत्येक मंडलाच्या वेढ्यांचे संयोजन करतात. याच प्रकारच्या एका सुधारलेल्या उपकरणाच्या साहाय्याने दहा अज्ञात चलांची समीकरण-प्रणाली सोडवून सर्वांत मोठ्या चलांच्या मूल्याच्या ०.१% पर्यंत अचूक मूल्ये काढता येतात. तसेच असंगत समीकरणांच्या बाबतीत लघुतम वर्ग निर्वाह (ज्याच्या निरीक्षित मूल्यांपासून असणाऱ्या फरकांच्या वर्गांची बेरीज किमान असते असा निर्वाह) मिळू शकतो.
समाकलन व अवकलन करणारी उपकरणे : या उपकरणांत अवकलज आणि समाकल यांची मूल्ये काढण्यासाठी विविध आकारांच्या पृष्ठांवरून फिरणारी चाके, विद्युत् मंडलातील भार किंवा प्रवाह, विशेष रीतीने तयार केलेल्या प्रकाशीय माध्यमातून पारगमन होणाऱ्या प्रकाशाचे परिणाम इत्यादींचा उपयोग करण्यात येतो.
क्षेत्रमापक : समाकलनाचा सर्वांत साधा उपयोग म्हणजे एखाद्या वक्राखालील क्षेत्रफळ काढणे हा होय. क्ष आणि य हे सहनिर्देशक असलेल्या वक्राचे समीकरण य = फ (क्ष) असे असेल, तर वक्र क्ष१ आणि क्ष२ हे भुज आणि य = ० हा अक्ष यांनी परिसीमित केलेले क्षेत्रफळ अ हे फ (क्ष) चा क्ष१ पासून क्ष२ पर्यंतचा समाकल घेऊन काढता येतो.
अ = क्ष१ò क्ष२ फ (क्ष) dक्ष
बऱ्याच वेळा वक्राखालील क्षेत्रफळाने एखादी अभियांत्रिकी दृष्ट्या महत्त्वाची राशी निर्देशित केली जाते. उदा., वाफेच्या एंजिनाच्या निर्देशकाने काढलेल्या वक्राखालील क्षेत्रफळावरून एंजिनाची कार्यक्षमता काढता येते. यामुळे अशा प्रकारचे क्षेत्रफळ जलद रीतीने काढण्यासाठी उपकरणाचा उपयोग करणे फायदेशीर ठरते.
अनियमित वक्राने परिसीमित केलेले क्षेत्रफळ काढण्यासाठी उपयोगी पडणाऱ्या पहिल्या उपकरणाचा शोध जे. एच्. हेरमान या बव्हेरियन अभियंत्यांनी १८१४ साली लावला. त्यानंतर अनेकांनी अशाच स्वरूपाची उपकरणे तयार केली. १८६० मध्ये तयार करण्यात आलेल्या एका क्षेत्रमापकाचे वर्णन पुढीलप्रणाणे आहे. (आ. १). या क्षेत्रमापकात एक फिरवता येण्याजोगी क्षैतिज (क्षितिज समांतर) वर्तुळाकार तबकडी असून त्यावर क्षेत्रफळ दर्शविणारे चाक ठेवलेले असते. खाचा पडलेल्या तीन चाकांनी आधार दिलेल्या एका चौकटीवर तबकडी ठेवलेली असते. ही चाके तीन समांतर रुळांवरून सरकू शकतात. तबकडीच्या खाली चौकटीवर एक दांडा बसविलेला असून तो खालच्या रुळांच्या लंब दिशेस हलू शकेल अशी व्यवस्था केलेली असते. तबकडीच्या अक्षाभोवती एक तार गुंडाळून व तिची टोके दांड्याच्या दोन टोकांना बांधून दांड्याच्या विस्थापनेच्या प्रमाणात तबकडीला कोनीय गती देता येते. दांड्याच्या एका टोकाला जोडलेली अनुरेखक सूची
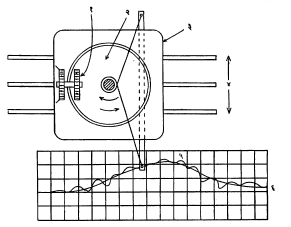
दिलेल्या वक्राच्या परिमितीवरून फिरविल्यास तबकडीचा मध्य आणि दर्शक चाकाचे प्रतल यांतील अंतर नेहमी वक्राच्या भुजाशी सम प्रमाणात राहते. यामुळे दर्शक चाकाच्या होणाऱ्या फेऱ्यांच्या संख्येवरून क्षेत्रफळ मोजता येते.
या क्षेत्रमापकामध्ये दर्शक चाकाची गती अंशतः सरकती असल्यामुळे मोजलेल्या क्षेत्रफळामध्ये थोडीफार चूक होण्याचा संभव असतो. याकरिता जेम्स मॅक्सवेल यांनी शुद्ध घरंगळत्या गतीचा उपयोग करणाऱ्या एका क्षेत्रमापकाचा आराखडा १८५५ साली तयार केला. त्यानंतर जेम्स टॉमसन यांनी १८७६ मध्ये तबकडी, गोल व चिती यांचा संयोग करून शुद्ध घरंगळती गती प्रत्यक्षात मिळविली.
याकोब आम्सलर या स्विस गणितज्ञांनी १८५४ च्या सुमारास ध्रुवीय क्षेत्रमापकाचा शोध लावला. हा क्षेत्रमापक रचनेत साधा आणि किंमतीने स्वस्त असल्यामुळे तो लवकर सर्वत्र प्रचारात आला.
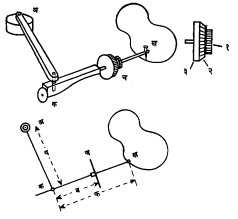
या उपकरणात (आ. २) अक आणि कख हे दोन दांडे एकमेकांना क येथे जोडलेले आहेत. अ हा बिंदू स्थिर ठेवलेला असून ख येथे सूची आहे. ज्या आकृतीचे क्षेत्रफळ पाहिजे असेल तिच्या परिमितीवरून सूची फिरवतात. कख या दांड्यावर तिरपा काप दिलेली कडा असलेले च हे चाक आहे. जेव्हा दांडा स्वत:शी लंब असलेल्या दिशेने सरकतो त्या वेळी हे चाक फिरेल, पण दांडा ज्या वेळी स्वत:च्या दिशेनेच सरकतो त्या वेळी चाक फिरणार नाही अशी व्यवस्था केलेली असते. चाक ज्या कोनातून फिरते तो कोन क्षेत्रफळाच्या सम प्रमाणात असतो. हा कोन चाकाला लावलेल्या मापपट्टीवरून मोजता येतो व या मापपट्टीचे योग्य प्रकारे अंशन (अंश पाडून निर्देशित करण्याची क्रिया) करता येते. क्षेत्रफळ मोजताना जर क हा बिंदू त्याच्या मूळ स्थानावर परत आला, तर ख या बिंदूने परिसीमित केलेले क्षेत्रफळ = कख गुणिले चाकाने कापलेले अंतर. सूची परिमितीवरून फिरविताना क ने अ भोवती पूर्ण प्रदक्षिणा केल्यास π (प२ –२ फब + ब२) हे स्थिर क्षेत्रफळ चाकावरील नोंदीत मिळवावे लागते (आ. २).
समाकलक :क्षेत्रमापकाचेच एक व्यापक स्वरूप असलेले समाकलक हे उपकरण आम्सलर यांनी १८५६ मध्ये तयार केले. या उपकरणाने एखाद्या आकृतीचे क्षेत्रफळ मिळण्याबरोबरच त्या आकृतीचे य = ० या अक्षाभोवतीचे परिबल (ò१/२ य २d क्ष) आणि निरूढी परिबल (म्हणजे कोनीय प्रवेगाला होणाऱ्या रोधाचे माप) ( ò१/३ य३ dक्ष) या राशीही मिळतात. हे उपकरण एका लांब पोलादी पट्टीवरील सरळ खाचेत दोन चाकांच्या साहाय्याने सरकविता येते. जर उपकरणाची सूची एखाद्या प्रतलीय आकृतीच्या परिमितीवरून फिरविल्यास मोकळ्या दंडावरील अंशांकित चाकावरून आम्सलर क्षेत्रमापकाप्रमाणेच आकृतीचे क्षेत्रफळ मिळते. एका बाह्य चाकावर उपकरणाच्या परिभ्रमण अक्षाभोवतीच्या परिबलाचे मूल्य दर्शविले जाते आणि या दोन चाकांवरील नोंदींवरून याच अक्षाभोवतीचे निरूढी परिबल काढता येते.
समाकलालेखक: क्षेत्रमापकाच्या साहाय्याने निश्चित समाकलाचे मूल्य काढता येते. काही वेळा आलेखाच्या स्वरूपात व्याख्यात केलेल्या एखाद्या फलनाचा अनिश्चित समाकल काढणे आवश्यक असते. म्हणजेच याकरिता य = फ (क्ष) या दिलेल्या वक्रानुसार त्याचा समाकल वक्र (म्हणजे झ =òयdक्ष) काढणारे उपकरण जरुरीचे असते. अशा प्रकारचा एक समाकलालेखक चार्ल्स बॉईज यांनी १८८१ मध्ये शोधून काढला. क्ष च्या कोणत्याही मूल्यासाठी उपकरणाने काढलेल्या वक्राचा उतार dझ/dक्ष हा त्याच क्ष च्या मूल्याकरिता दिलेल्या वक्राच्या भुजाच्या (य च्या मूल्याच्या) सम प्रमाणात असतो. या उपकरणाची चौकट म्हणजे एक प्रकारच्या टी-गुण्यासारखी असते. हा गुण्या क्षैतिज सरळ कडेवर सरकू शकतो. ह्या गुण्याचा मध्य (म) दिलेल्या वक्राच्या क्ष अक्षावरून सरकतो. एक दांडा म या मध्यातूनच नेहमी जाईल अशा तऱ्हेने जोडलेला असून त्यावर स ही सूची असते. ही सूची गुण्याच्या उभ्या रेषेवरून सरकू शकेल अशी व्यवस्था केलेली असते. त्यामुळे ती कोणत्याही स्वरूपाच्या वक्रावरून फिरविता येते. म पासून टी- गुण्याच्या उभ्या रेषेपर्यंतचे अंतर स्थिर (क) असते. यामुळे मस या दांड्याच्या उताराचा कोन अशा प्रकारे होतो की, त्या कोनाचे स्पर्शक गुणोत्तर हे दिलेल्या वक्राचा भुज भागिले क इतके होते. अशा प्रकारे मस चा उतार हा काढावयाच्या समाकल वक्राच्या उताराइतकाच असतो. समाकल वक्र काढण्यासाठी एका तीन चाकी गाडीसारख्या योजनेचा उपयोग करण्यात येतो. या गाडीचे पुढले चाक (च) जरूर त्याप्रमाणे वळविता येते. बहिश्वक्री (एका स्थिर अक्ष असणाऱ्या चाकाच्या आतल्या किंवा बाहेरच्या बाजूवरून एक वा अधिक दंतचक्रे फिरतात अशा) दंतचक्र मालेने हे चाक मस ला समांतर राहील अशी व्यवस्था केलेली असते. हे चाक फक्त त्याच्या प्रतलाच्या दिशेतच हलू शकते व ते नेहमी टी–गुण्याच्या वाढविलेल्या उभ्या रेषेवरच असल्यामुळे ते एखाद्या कार्बन कागदावरून नेल्यास आवश्यक तो समाकल वक्र काढता येतो.

व्यापारी स्वरूपाचा पहिला समाकलालेखक आबडांक अबॅकानोवित्झ यांनी साधारणपणे बॉईज यांच्या शोधाच्या वेळीच पण स्वतंत्रपणे तयार केला (आ. ३). या उपकरणाच्या रचनेत नंतर सुधारणा करण्यात येऊन त्याचे मोठ्या प्रमाणात उत्पादन करण्यात आले.
हरात्मक विश्लेषक :काही जटिल फलनांचे किंवा वक्रांचे अनेक सरल हरात्मक गतींच्या बेरजेच्या स्वरूपात निदर्शन करता येते. फ्रेंच गणितज्ञ फूर्ये यांनी उष्णतेचे विसरण (रेणू एकमेकांत मिसळून होणारे उष्णतेचे वहन) आणि प्रेषण यांसंबंधीच्या प्रश्नांत या निदर्शनाचा प्रथम उपयोग केला. संदेशवहन मार्ग, विद्युत् शक्ती संयंत्रे (यंत्रसंच), गोंगाट, वाद्ये इत्यादींसंबंधीच्या प्रश्नांत असा निदर्शनाचा फार उपयोग होतो. या विषयांतील बरेचसे विश्लेषण संख्यात्मक पद्धतीने केले जात असले, तरी काही वेळा हरात्मक विश्लेषकही वापरले जातात [→ हरात्मक विश्लेषणफूर्ये श्रेढी ].
अवकल विश्लेषक: अभियांत्रिकी व भौतिकी या विषयांतील प्रश्न बऱ्याच वेळा अवकल समीकरणाच्या स्वरूपात मांडण्यात येतात. व्यवहारात आढळणाऱ्या अवकल समीकरणांपैकी फारच थोड्यांचे निर्वाह त्रिकोणमितीय, बेसेल इ. साध्या फलनांच्या स्वरूपात काढता येतात. बऱ्याच वेळा अभियांत्रिकीमध्ये संख्यात्मक किंवा आलेख स्वरूपात निर्वाह मिळणे शक्य असल्यास रीतसर स्वरूपाच्या निर्वाहाची आवश्यकताही नसते असे संख्यात्मक किंवा आलेख स्वरूपाचे निर्वाह मिळविण्यासाठी विविध प्रकारचे अवकल विश्लेषक तयार करण्यात आले आहेत. विद्युत् यंत्रांचे अभिकल्प, अणूंनी प्रकीर्णित केलेले (विखुरलेले) इलेक्ट्रॉन, स्वयंचलित औद्योगिक नियंत्रण पद्धतींचे कार्यमान, प्रक्षेपित वस्तूंचे गतिमार्ग (उदा., तोफेतून सोडलेला गोळा) इ. विविध क्षेत्रांतील प्रश्न सोडविण्यासाठी अवकल विश्लेषकांचा उपयोग होतो.
लॉर्ड केल्व्हिन यांनी १८७६ मध्ये अवकल विश्लेषकाचे तत्त्व मांडले होते. मॅसॅचूसेट्स इन्स्टिट्यूट ऑफ टेक्नॉलॉजी येथील व्हन्नीव्हार बुश व त्यांचे सहकारी यांनी अवकल विश्लेषकाचा विकास करण्यात महत्त्वाचे कार्य केले. १९२८ साली त्यांनी पहिला अवकल विश्लेषक तयार केला. याच उपकरणात थोड्याफार सुधारणा करून शैक्षणिक व औद्योगिक क्षेत्रांत उपयोगी पडतील अशी उपकरणे अमेरिकेत आणि यूरोपात प्रचारात आली.
अवकल समीकरण सोडविण्यासाठी समाकलन करावे लागते. त्याकरिता अवकल विश्लेषकात पूर्वीच्या क्षेत्रमापकात वापरण्यात आलेल्या तबकडी व चाक यांच्या संयोगाचा समाकलक म्हणून उपयोग करतात. या प्रयुक्तीने झ = ∫ यdक्ष हे समाकलन करण्यात येते. ह्या समाकलकात क्ष हे तबकडीचे कोनीय विस्थापन, य हे तबकडीच्या मध्यापासून समाकलक चाकाचे अंतर आणि झ हे समाकलक चाकाचे परिणामी कोनीय विस्थापन होय. क्ष आणि य ह्या राशी प्रत्येकी एकेका दंडाच्या कोनीय विस्थापनाने निदर्शित केल्या जातात व त्यांची बेरीज एका यांत्रिक विभेदी चक्रमालेने (ज्यामध्ये एका चक्राने फिरविण्यात येणाऱ्या दोन दंडांना सापेक्ष गती देता येते अशा चक्रमालेने) केली जाते. ही विभेदी चक्रमाला अशा प्रकारे जोडलेली असते की, एक तिसरा दंड झ (= क्ष +य) इतक्या कोनातून फिरेल. स्थिरांकाने गुणावयाचे असल्यास त्यासाठी योग्य अशा दंतचक्राची योजना केलेली असते. जर क्ष हा चल निदर्शित करणारा दंड व य हा चल निदर्शित करणारा दंड यांतील परिगती गुणोत्तर क असेल, तर य = कक्ष असे निदर्शित होते. स्वेच्छ किंवा प्रयोगसिद्ध फलने ‘आदान कोष्टकांवरʼ आलेख स्वरूपात काढून विश्लेषकात वापरण्यात येतात. विश्लेषकाने योग्य ते कार्य करून काढलेला निर्वाह ‘प्रदान कोष्टकांवरʼ किंवा ठराविक वेळी संख्यात्मक मूल्यांच्या स्वरूपात छापून मिळतात.
बुश अवकल विश्लेषक संपूर्णपणे यांत्रिकी स्वरूपाचा असून त्याचे आकारमानही अवाढव्य आहे. त्यातील संगणन करणाऱ्या घटकांची जोडणी दंड व दंतचक्रे यांच्या साहाय्याने केलेली आहे. हा विश्लेषक वापरण्यासाठी सोडवावयाची समीकरणे प्रथम समाकलन, बेरीज, स्थिरांकाने गुणाकार किंवा फलनीय संबंध या गोष्टी असलेल्या समीकरणांच्या संचाच्या स्वरूपात मांडावी लागतात. या समीकरणांवरून दंड, समाकल, विभेदी चक्रमाला आणि दंतचक्रे यांच्या चिन्हांचा समावेश असलेली कच्ची आकृती तयार करण्यात येते. त्यानंतर विश्लेषकातील घटकांची या आकृतीनुसार जुळवाजुळव करण्यात येते.
विश्लेषणाच्या कार्याचे नियंत्रण व त्यातील घटकांची दिलेल्या प्रश्नानुसार जुळवणी करणे या बाबतीत बुश विश्लेषकापेक्षा अधिक वेगवान व सुटसुटीत असलेला रॉकफेलर अवकल विश्लेषक १९४५ मध्ये प्रचारात आला. या विश्लेषकात दंडाच्या परिभ्रमणाचे फिरत्या विद्युत् धारित्रांच्या (विद्यूत् भार साठविणाऱ्या साधनांच्या) साहाय्याने विद्युत् संदेशांत रूपांतर होते. या संदेशानुसार विश्लेषकातील चलित्रांनी (विद्युत् मोटारीची) गती नियंत्रित करण्यात येते. ह्या चलित्रांनी फिरणाऱ्या दंडांची स्थिती जवळजवळ नियंत्रक दंडांच्या स्थितीसारखीच राहील अशा प्रकारे चलित्रांची गती नियंत्रित करण्यात येते. विद्युत् शक्तीने चालविलेल्या स्विचांनी नियंत्रक संदेश जरूर त्या ठिकाणी पोहोचविले जातात. दिलेल्या प्रश्नानुसार विश्लेषकाची जुळवणी करण्यासाठी जरूर ती माहिती कागदी पट्ट्यांवर छिद्रित स्वरुपात नोंदवितात व काही थोड्या मिनिटांतच या पट्ट्या स्वयंचलित रीत्या जरूरीप्रमाणे विद्युत् स्विचांची जोडणी करतात.
सामान्य अवकल समीकरणे सोडविण्यासाठी वर वर्णन केलेली उपकरणे अद्यापही थोड्याफार प्रमाणात वापरली जातात. तथापि सदृश प्रकारच्या संगणकाने अशा प्रकारची समीकरणे फार जलद सोडविता येत असल्यामुळे या उपकरणांचा वापर कमी होत चालला आहे. सदृश संगणकाला इलेक्ट्रॉनीय अवकल विश्लेषक असेही म्हणतात.
आंशिक अवकल समीकरणे सोडविण्याची उपकरणे :या प्रकारच्या उपकरणांत स्थितिस्थापक पटले, संवाहक पत्र्यातील विद्युत् प्रवाह वा ध्रुवित (एकाच प्रतलात कंप पावणारा) प्रकाश यांचा उपयोग करण्यात येतो. इलेक्ट्रॉनीय नलिकांतील वर्चसांसंबंधीची अवकल समीकरणे सोडविण्यासाठी व या वर्चसाच्या प्रभावाखाली होणारे इलेक्ट्रॉनांचे मार्गक्रमण पूर्वसूचित करण्यासाठी वापरण्यात येणारी प्रयुक्ती ही अशा प्रकारच्या उपकरणाचे उत्तम उदाहरण आहे. विद्युत् वर्चस् व ताणलेले स्थितिस्थापक पटल हे एकाच प्रकारच्या आंशिक अवकल समीकरणांची पूर्तता करतात. यामुळे इलेक्ट्रॉनीय नलिकांचा अभ्यास व अभिकल्प करण्यासाठी एकविध (सर्वत्र सारखा) ताण दिलेल्या रबरी पटलाचा उपयोग करतात. पटल आडवे ठेवलेले असल्यामुळे त्यांची उदग्र (उभ्या दिशेतील) विस्थापने वर्चस् समीकरणांची पूर्तता करतात. ठोकळ्यांच्या आधाराने किंवा चिमट्यांनी मर्यादा मूल्ये निर्माण केली, तर या पटलाद्वारे निर्देशित मर्यादा अटींनुसार वर्चस् प्रश्नाचा निर्वाह मिळू शकतो.
संदर्भ : 1. Ginsburg, S. An Introduction to Mathematical Machine Theory, Reading, Mass., 1962.
2. Murray, F. J. Mathematical Machines, New York, 1961.
भदे, व. ग.
“