कोन : एखाद्या रेषेने तीवरील एका बिंदूभोवती, एकाच प्रतलात (पातळीत) केलेल्या परिभ्रमणाचे मोजमाप म्हणजे कोन होय. जेव्हा दोन रेषा परस्परांत छेदतात तेव्हा त्यांतील कोणतीही एक रेषा छेदबिंदू भोवतीच्या ज्या परिभ्रमणाने दुसरीच्या स्थानी आणता येईल, त्या परिभ्रमणास त्या दोन रेषांमधील कोन म्हणतात. उदा., आकृतीत दाखविल्याप्रमाणेकखआणिकगया दोन रेषाकमध्ये छेदतात. बाणाने दाखविल्याप्रमाणे प्रतिघटीवत(घड्याळातील काट्यांच्या गतीच्या विरुध्द) दिशेने कख ही रेषा क भोवती फिरवून कग रेषेशी जुळती करता येईल. अशा परिभ्रमणास कोन खकग म्हणतात आणि तो ∠ खकग असा दर्शवितात. कख आणि कग यांना कोन भुजा म्हणतात. वरील उदाहरणाप्रमाणे परिभ्रमण प्रतिघटीवत असेल, तर कोन धन मानतात आणि परिभ्रमण घटीवत असेल, तर झालेला कोन ऋण मानण्याची प्रथा आहे.
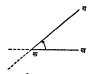
वरील उदाहरणात जरकखनेकभोवती एक प्रदक्षिणा पूर्ण कोली तर ती मूळस्थानी परत येईल. या परिभ्रमणात जो कोन होईल त्याचे ३६० सारखे भाग केले असता त्यांतील प्रत्येकास अंश म्हणतात. म्हणजेच एक पूर्ण प्रदक्षिणा= ३६० अंश. एका अंशाचे ६० सारखे भाग केले असता त्या प्रत्येकास कला (मिनिट) व प्रत्येक कलेचे ६० सारखे भाग केले असता त्या प्रत्येकास विकला (सेकंद) म्हणतात. अंश, कला आणि विकला दर्शविण्यासाठी त्या त्या आकड्यांच्या डोक्यावर अनुक्रमे ०, ‘, ”, या चिन्हांचा उपयोग करतात. एका पूर्ण प्रदक्षिणेचे चार सारखे भाग केले, तर त्यांतील प्रत्येकास काटकोन म्हणतात. अर्थातच एक काटकोन = ९०० . जेव्हा दोन रेषांमधील कोन काटकोन असतो तेव्हा त्या परस्परांस लंब आहेत असे म्हणतात. ९०० पेक्षा कमी असलेल्या कोनास लघुकोन, ९०० पेक्षा जास्त व १८०० पेक्षा कमी असल्यास विशालकोन, १८०० ला सरळकोन आणि १८०० पेक्षा जास्त असल्यास प्रविशालकोन अशी नावे दिलेली आहेत. वरील विवेचनावरून असे दिसून येईल की, कोन कितीही अंशाचा वा कोणत्याही चिन्हाचा असू शकतो. उदा ७८०० कोन म्हणजे (परिभ्रमण करणाऱ्या) रेषेने दोन प्रदक्षिणा पूर्ण करून आणखी ६०० चे परिभ्रमण केले कारण ७८०० = २ × ३६००+ ६००. तसेच -४३०० म्हणजे घटीवत दिशेने एक पूर्ण प्रदक्षिणा आणि ७०० होत.
कोन मोजण्याच्या आणखी एका पद्धतीत एका काटकोनाचे १०० अंश (डिग्री), प्रत्येक अंशाची १०० मिनिटे (किंवा ग्रेड) व प्रत्येक मिनिटाचे १०० सेकंद अशी विभागणी करतात. या पध्दतीस शतमान पध्दती म्हणतात. ही फारशी वापरात नाही.
सैध्दांतिक विवरणात अरीयमान (रेडियन) नावाची कोन मोजण्याची पद्धती रूढ आहे. दोन रेषांचा छेदबिंदू मध्य कल्पून एकक त्रिज्येचे वर्तुळ काढले असता त्या वर्तुळाच्या परिघाचा जो भाग त्या दोन रेषांमध्ये समाविष्ट होतो त्याची लांबी म्हणजेच त्या दोन रेषांमधील कोनाचे अरीयमान होय. ज्यावेळी ही लांबी एककाइतकीच असेल त्यावेळी होणारा कोन एक अरीय असतो. एकक त्रिज्येच्या वर्तुळाचा परिघ २ π इतक्या लांबीचा असल्याने एक संपूर्ण प्रदक्षिणा म्हणजे २ πअरीये होय. म्हणजेच १ काटकोन = ९०० = π/२ अरीये असे लिहिता येईल. यावरून दोन्ही पध्दतींतील कोनांच्या मूल्याचे परस्पर रूपांतर करता येते.
ज्यावेळी दोन रेषा एकमेकींस छेदत नाहीत (म्हजेच त्या वितलीय असतील) तेव्हा त्यांतील कोनाची व्याख्या पुढीलप्रमाणे करतात. कोणताही एक बिंदू घेऊन त्यातून दिलेल्या दोन्ही रेषांना समांतर रेषा काढल्या असता त्यांमध्ये होणारा कोन म्हणजेच दिलेल्या वितलीय रेषांमधील कोन होय.
द्वितल कोन : जेव्हा दोन प्रतले परस्परांस एका रेषेत छेदतात तेव्हा त्यांमधील द्वितल कोनाची व्याख्या पुढीलप्रमाणे करतात. समजा, क आणि ख ही दोन प्रतलेयरया रेषेत परस्परांस छेदतात. ब हा यर वरील कोणताही बिंदू घेतला आणि ब मधून बप ही क प्रतलावर यर ला लंब अशी रेषा काढली व तशीच बफ ही यर ला काटकोन करणारी रेषा ख प्रतलावर काढली, तर ∠ पबफ हा क आणि ख या दोन प्रतलांतील कोन होय.
त्रितल कोन व बहुतल कोन : जेव्हा तीन प्रतले एका बिंदूतून जातात तेव्हा त्यांच्या योगे त्रितल कोन तयार होतो. त्याच प्रमाणे एकाच बिंदूतून जाणाऱ्या अनेक प्रतलांयोगे बहुतल कोन तयार होतो. बहुतल कोन मोजण्याची पद्धती ही अरीयमान पध्दतीचे व्यापक स्वरूप आहे. ती अशी : कोन तयार करणाऱ्या प्रतलांचा छेदबिंदू हा मध्य कल्पून जर एकक त्रिज्येचा गोल काढला, तर त्या गोल पृष्ठाचा जो भाग त्या प्रतलांमध्ये समाविष्ट होतो, त्याचे क्षेत्रफळ म्हणजे त्या बहुतल कोनाचे मान होय. एकक त्रिज्येच्या गोलाचे एकूण पृष्ठफळ ४Π इतकेच असल्याने जास्तीत जास्त एवढाच बहुतल कोन शक्य आहे, हे उघड आहे.
घन कोन : ब हा कोणताही बिंदू आणि कोणताही एक आवृत्त (बंद) वक्र घेतला व त्यावरील प्रत्येक बिंदूतून ब शी जोडणाऱ्या रेषा काढल्या तर या सर्व रेषांनी बध्द असा ब बिंदूशी घन कोन तयार होतो. यामध्ये आवृत वक्र जर बहुभुज असेल तर बहुतल कोन मिळेल. घन कोन मोजण्याची पध्दती बहुतल कोन मोजण्याच्या पध्दतीप्रमाणेच आहे, कोनबिंदू मध्य कल्पून एकक त्रिज्येचा गोल घेतला, तर घन कोन तयार करणाऱ्या रेषांमध्ये असलेल्या गोल पृष्ठाचे क्षेत्रफळ म्हणजेच घन कोनाचे मान होय.
वक्रांमधील कोन : दोन वक्र जर परस्परांस छेदत असतील, तर त्यांच्या छेदबिंदूशी त्या दोन्ही वक्रांना स्पर्शिका (स्पर्शरेषा) काढल्यास त्या स्पर्शिकांमधील कोन म्हणजेच त्या दोन वक्रांमधील कोन होय.
पृष्ठांमधील कोन : दोन पृष्ठांच्या समाईक बिंदूशी जर दोन्ही पृष्ठांना प्रलंब (स्पर्श करणाऱ्या प्रतलाला काढलेली लंबरेषा) काढले, तर त्या प्रलंबामध्ये असलेला कोन म्हणजेच त्या पृष्ठांमधील कोन होय.
आगाशे, क.म.
“