तापायनिक उत्सर्जन

तापायनिक उत्सर्जन : निर्वातामध्ये धातू वा तत्सम घन पदार्थ तापविले असता, त्यापासून मुख्यतः इलेक्ट्रॉनांचे उत्सर्जन होते. या क्रियेस तापायनिक उत्सर्जन आणि अशा प्रकारे उत्सर्जित झालेल्या इलेक्ट्रॉनांना तापायन (थर्मिऑन) असे संबोधतात. तप्तावस्थेतील धातूंच्या आसमंतातील हवेस विद्युत् संवाहक गुणधर्म प्राप्त होतो. हा आविष्कार बऱ्याच वर्षांपासून माहीत होता. फ्रेडरिक गथ्री (१८७३) आणि जे. एलस्टर व एच्. एफ्. गाइटेल (१८८० ते १८९०) यांनी यासंबंधी काही प्रयोगही केले होते. १८८३ मध्ये टॉमस एडिसन यांनी असे सिद्ध केले की, तापायनिक उत्सर्जनाच्या क्रियेत ऋण विद्युत् भरित कण उत्सर्जित केले जातात. या महत्त्वाच्या शोधाला कधीकधी ⇨ एडिसन परिणाम असे म्हणतात. १९०२ मध्ये ओ. डब्ल्यू. रिचर्ड्‌सन यांनी प्रथम तापायनिक उत्सर्जनाचे सैद्धांतिक स्पष्टीकरण दिले. त्यांना या शोधाबद्दल आणि त्यावरील प्रायोगिक संशोधनाबद्दल १९२८ सालचे भौतिकीचे नोबेल पारितोषिक देण्यात आले.

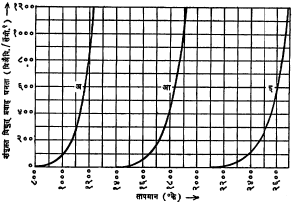
तापानियक उत्सर्जक इलेक्ट्रॉनीय नलिकेत [→ इलेक्ट्रॉनीय प्रयुक्ति] ऋणाग्र म्हणून वापरतात. औष्णिक ऊर्जेचे सरळ विद्युत् ऊर्जेत रूपांतर करण्याकरिता वापरण्यात येणाऱ्या काही प्रयुक्तीमध्येसुद्धा हे वापरले जातात. तात्त्विक दृष्ट्या जरी कोणत्याही धातूचा उपयोग इष्ट परिस्थितीत उत्सर्जक म्हणून करता येण्यासारखा असला, तरी प्रत्यक्ष व्यवहारात बहुशः शुद्ध टंगस्टन, थोरियममिश्रित (थोरिएटेड) टंगस्टन, ऑक्साइडलेपित निकेल इ. धातू वा मिश्रधातू  यांचाच उत्सर्जक  म्हणून उपयोग करतात. उत्सर्जकाला कार्यकारी करण्यासाठी लागणारे तापमान, त्याची उत्सर्जनक्षमता, त्याचे उपयुक्त आयुर्मान हे निकष त्याची उपयुक्तता ठरविण्याकरिता लावतात. वरील उत्सर्जकांचे कार्यवैशिष्ट्य इ. त्यांच्या उपयोगाच्या दृष्टीने उपयुक्त अशी माहिती कोष्टकात व आ. १ मध्ये दिली आहे. याबाबतीत लक्षात ठेवण्यासारख्या गोष्टी पुढीलप्रमाणे होत. उत्सर्जकाचे तापमान दुप्पट केले असता इलेक्ट्रॉन उत्सर्जनाचे प्रमाण एक कोटीपट वाढू शकते. नीच कार्यकारी तापमान वापरले असता औष्णिक प्रेषणामुळे होणारी शक्तीतील घट कमी असते, उत्सर्जकाचे उपयुक्त आयुष्यही जास्त असते आणि तापमानामुळे मंडलातील घटकाच्या होणाऱ्या संभाव्य नुकसानीचे प्रमाण कमी राहते.

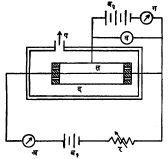प्रयोगात्मक अभ्यास : तापायनिक उत्सर्जन क्रियेचा अभ्यास करण्यासाठी सर्वसाधारणपणे उपयोगात आणली जाणारी उपकरणाची रचना आ. २ मध्ये दाखविली आहे. त ही टंगस्टन उत्सर्जकाची तार द या पोकळ धातूच्या दंडगोलाच्या (पट्टिकेच्या) अक्षावर बसविली आहे. ही दोन्ही एका बंद काचेच्या भांड्यात बंदिस्त केली असून प ही नळी निर्वात पंपाला जोडून त्याच्या साहाय्याने त्यामध्ये निर्वात स्थिती निर्माण करता येते. त ही उत्सर्जक तार ब_१ या विद्युत् घटाच्या साहाय्याने तापविता येते. याच मंडलात अ हा विद्युत् प्रवाहात्मक आणि र हा रोध जोडला आहे. र चे मूल्य कमीजास्त करून या मंडलातील विद्युत् प्रवाहाचे परिमाण आणि अंती त चे तापमान बदलता येते. मंडलातील रोध र चे मूल्य आणि विद्युत् प्रवाहाचे मूल्य यांवरून त चे तापमान काढता येते. तापायनिक उत्सर्जनजन्य विद्युत् प्रवाह I_P मोजण्याकरिता ग हा विद्युत् प्रवाहमापक वापरला जातो, तर त आणि द यांमधील चर्चोभेद (विद्युत् स्थितींतील फरक) V_P हा व या व्होल्टमापकाने मोजला जातो. ब_२ या विद्युत् घटाच्या साहाय्याने वरील वर्चोभेद मिळतो. काही उत्सर्जकांमधून, विशेषतः त्यांचे तापमान कमी असताना, सुरुवातीस घन भारित आयनांचे (विद्युत् भारित अणू वा रेणूंचे) सुद्धा उत्सर्जन होते असे दिसून आले. अधिक संशोधन केल्यावर असे आढळले की, हा परिणाम त्या उत्सर्जकाच्या पृष्टभागावरील अधिधारित (पृष्टभागावर धरून ठेवलेल्या) वायूमुळे होत असावा. उत्सर्जक बराच काळ पर्यंत उच्च निर्वातात ठेऊन उच्च तापमानाला तापविला असता हे आयन उत्सर्जन कमी होत जाऊन शेवटी नगण्य होते, असे आढळले. तापायनिक उत्सर्जनावरील सर्व प्रयोगांत या गोष्टीची दखल घ्यावी लागते.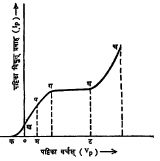 

V_p–I_p अभिलक्षण वक्र : आदर्श परिस्थितीत V_p वाढवीत गेले असता I_p मध्ये होणारे परिवर्तन आ. ३ मध्ये दाखविल्यासारखे असते. या V_p–I_p वक्रास तापायनिक उत्सर्जनाचा अभिलक्षण वक्र असे म्हणतात. आकृतीच्या सुलभतेकरिता कख या विभागाचा मापक्रम विवर्धित स्वरूपात दाखविला आहे. हा भाग तापयनांना उत्सर्जकातून बाहेर पडतानाच काही गतिज ऊर्जा असते, हे दर्शवितो. वक्रामधील खग या भागातील विद्युत्प्रवाहास ‘पर्यावेशनिर्धारित’ विद्युत् प्रवाह असे म्हणतात. याचे सैद्धांतिक विश्लेषण ज्यांनी केले त्यांच्या नावावरून यास ‘चाईल्ड–लॅंगमूर विभाग’ असे म्हणतात. या भागाचे विवेचन पुढीलप्रमाणे केले जाते. उत्सर्जकातून दर सेकंदास जेवढे इलेक्ट्रॉन बाहेर पडतात ते सर्वच द पट्टिकेपर्यंत पोहोचू शकत नाहीत. उत्सर्जकाचे तापमान उच्च असल्यामुळे हे तापयानिक इलेक्ट्रॉन लहानमोठ्या ऊर्जेने बाहेर पडतात. या सर्व इलेक्ट्रॉनिकांचा वेग सारखाच नसतो, हे येथे लक्षात घेणे आवश्यक आहे. जे इलेक्ट्रॉन पट्टिकेपर्यंत जाऊ शकत नाहीत ते ऊत्सर्जकाच्या आसमंतात जमा होऊन ‘पर्यावेश’ (उत्सर्जकाकडून पट्टिकेकडे जाणाऱ्या इलेक्ट्रॉन प्रवाहाला प्रतिबंध करणाऱ्या इलेक्ट्रॉनांचा ढग) निर्माण करतात. आ. ३ वरून असे दिसेल की, प या बिंदूने दर्शविलेल्या परिस्थितीत उत्सर्जक तापायनिक विद्युत् प्रवाहाचे मूल्य घट एवढे असते, तर पट्टिका प्रवाह त्यापेक्षा कमी म्हणजे पम एवढा आहे. या जमा झालेल्या इलेक्ट्रॉनांमुळे उत्सर्जकाच्या नजीक एक पर्यावेशजन्य विद्युत् क्षेत्र निर्माण होते व ते उत्सर्जकातून बाहेर पडणाऱ्या इलेक्ट्रॉनांना पट्टिकेकडे जाण्यास विरोध करते. हे प्रतिसारक क्षेत्र विशेषतः मंदगती इलेक्ट्रॉनांना उत्सर्जकाकडे परत पोहोचविते. पट्टिकेपर्यंत दर सेकंदास पोहोचणाऱ्या इलेक्ट्रॉनांची संख्या उत्सर्जकातून निव्वळ बाहेर जाणाऱ्या त्यांच्या संख्येएवढी होते आणि अशा तऱ्हेने उत्सर्जकातून बाहेर पडणाऱ्या इलेक्ट्रॉनांच्या संख्येत समतोल निर्माण होतो. आता जर पट्टिका वर्चस् वाढविले, तर हा समतोल बदलता येतो. यामुळे उत्सर्जकाच्या नजीकच्या भागातील पर्यावेश कमी होतो. त्यामुळे उत्सर्जकाकडे परत पोहोचणाऱ्या इलेक्ट्रॉनांची संख्या कमी होते व अशा रीतीने पट्टिका प्रवाह वाढत जातो. उत्सर्जकाचे तापमान स्थिर ठेवले, तर या अवस्थेत मिळणाऱ्या विद्युत् प्रवाहाचे मूल्य खाली दिलेल्या चाइल्ड–लॅंगमूर नियमाप्रमाणे मिळते.

हे सूत्र दंडगोल आकाराच्या द्विप्रस्थ (दोन विद्युत् अग्रे असलेल्या) नलिकेलाच लागू पडते. येथे Ip = पट्टिका विद्युत् प्रवाह, Vp = ऋणाग्र व धनाग्र यांमधील वर्चोभेद, I पट्टिका लांबी आणि

इलेक्ट्रॉनीय नलिकांचा विवर्धक इ. म्हणून उपयोग केला जातो तेव्हा त्या बहुशः याच अवस्थेत कार्यान्वित केल्या जातात. Vp आणि Ip यांमधील संबंध रेखात्मक (एकघाती स्वरूपाचा) नाही, याकडे लक्ष वेधण्यासारखे आहे. अशा प्रकारचे अभिलक्षण वक्र असणाऱ्या प्रयुक्तीस अरेखीय मंडल घटक असे म्हणतात. या प्रकारच्या घटकांचे व्यवहारात विविध उपयोग केले जातात.

पट्टीका वर्चस् खूप वाढविले असता उत्सर्जकापासून बाहेर पडणारे सर्व इलेक्ट्रॉन पट्टिका आपल्याकडे ओढून घेते. या अवस्थेत पर्यावेश शून्य होतो व आता विद्युत् प्रवाहाचे मूल्य फक्त उत्सर्जकाच्या तापमानावरच अवलंबून राहते, असे दिसते. या वेळी Vp चे मूल्य वाढविले, तरी Ip मूल्य स्थिरच राहते. आ. ३ मधील वक्राचा गघ हा भाग ही स्थिती दाखवितो. गघ हा भाग (जवळजवळ) क्ष अक्षास समांतर आहे, हे लक्षात घेण्याजोगे आहे. या अवस्थेतील विद्युत् प्रवाहास ‘संपृक्त’ विद्युत् प्रवाह अथवा ‘तापमान निर्धारित’ विद्युत् प्रवाह असे म्हणतात. याचे मूल्य ओ. डब्ल्यू. रिचर्ड्‌सन व एस्, दुशमान यांच्या नियमानुसार मिळते.

संपृक्त विद्युत् प्रवाह व उत्सर्जकाचे तापमान यांमधील संबंध, रिचर्ड्‌सन–दुशमान नियम : घन अवस्थेतील धातूच्या अणूंच्या सर्वांत बाहेरील कक्षांत असणाऱ्या इलेक्ट्रॉनांना संयोजी इलेक्ट्रॉन असे म्हणतात. धातूमधील अणू (वायू व द्रव यांच्या अणूंच्या मानाने) अत्यंत जवळजवळ असल्यामुळे आसपासच्या अणूंच्या विद्युत् क्षेत्रांचा या संयोजी इलेक्ट्रॉनांवर क्षोभक परिणाम होतो. त्यामुळे या संयोजी इलेक्ट्रॉनांपैकी काही इलेक्ट्रॉनविशिष्ट अणूंचे भाग म्हणून न राहता, ते अणूंच्या अवकाश वितरणामुळे निर्माण झालेल्या स्फटिक जालकात मुक्त संचार करू शकतात, असे मानले जाते. या इलेक्ट्रॉनांच्या विद्युत् भारामुळे त्यांमध्ये परस्परक्रिया होत असते. या कारणामुळे त्यांच्यामधील ऊर्जा वितरण रूढ मॅक्सवेल–बोल्टस्‌मान सांख्यिकीप्रमाणे न होता त्याचे नियमन ⇨ पुंजयामिकीनुसार असलेल्या फेर्मीडिरॅक सांख्यिकीप्रमाणे होत असते, असे दाखविता येते [→ सांख्यिकीय भौतिकी]. मुक्त इलेक्ट्रॉनांचे तापमान हे निरपेक्ष शून्यापर्यंत (–२७३·१^° से. पर्यंत) कमी केले, तरीही त्या सर्वांची ऊर्जा रूढ भौतिकीनुसार शून्य व्हावयास पाहिजे. फेर्मी–डिरॅक सांख्यिकीप्रमाणे या स्थितीतही इलेक्ट्रॉनांमध्ये शून्यापासून एका विवक्षित कमाल मर्यादेपर्यंत ऊर्जामूल्ये आढळतात. या कमाल ऊर्जा मूल्याला फेर्मी ऊर्जा असे म्हणतात. हिचे मूल्य निरनिराळ्या धातूंकरिता निरनिराळे असते.

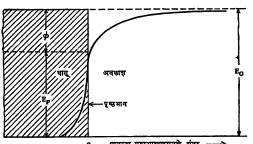
घन अवस्थेतील धातूंच्या स्फटिक जालकामधून ‘मुक्त’ इलेक्ट्रॉन सहज संचार करीत असले, तरी ते धातूच्या बाहेर पडून अवकाशात येऊ शकत नाहीत, असे दाखवता येते. आ. ४ मध्ये धातूमधील मुक्त इलेक्ट्रॉनांची ऊर्जा धातूच्या पृष्टभागापासून त्याच्या अंतराबरोबर कशी बदलते, हे दाखविले आहे. धातूच्या आतील भागातील वक्राचा आकार अंदाजानेच निश्चित केला गेला आहे. इलेक्ट्रॉनाला जर अवकाशात मुक्त अवस्थेत यावयाचे असेल, तर त्यास किमान E_G (आ. ४) एवढी एकूण ऊर्जा असणे आवश्यक आहे, हे आकृतीवरून दिसते. या इलेक्ट्रॉनांपैकी सर्वांत जास्त ऊर्जा फेर्मी ऊर्जेच्या (E_F) इतकी असू शकते, असे मानण्यात येते. उत्सर्जकाचे तापमान वाढविले असता त्यांपैकी काही ऊर्जा मुक्त इलेक्ट्रॉनांना मिळू शकते. त्यामुळे कमीतकमी E_G–E_F=f एवढी ऊर्जा उत्सर्जकाचे तापमान वाढवून इलेक्ट्रॉनांना दिली असता ते त्यापासून निसटून बाहेर अवकाशात येऊ शकतात.E_G याला धातूचे सकल कार्यफलन असे म्हणतात, तर f यास निव्वळ कार्यफलन असे संबोधितात. तटबंदीच्या आत ठेवलेल्या एखाद्या वस्तूला तट पार करण्यासाठी ज्याप्रमाणे तटबंदीच्या उंचीच्या प्रमाणानुसार काही किमान ऊर्जा देणे आवश्यक ठरते, त्याचप्रमाणे अंतर्गत इलेक्ट्रॉनांना बाहेर येण्यासाठी काही किमान ऊर्जा द्यावी लागते. ही ऊर्जा विद्युत् वर्चसाच्या स्वरूपात व्यक्त करता येते म्हणून हे आंतरिक इलेक्ट्रॉन जणू काही विशिष्ट उंचीच्या वर्चस् तटामध्ये बंदिस्त केले गेले आहेत, असे मानले जाते. तप्त धातूपासून होणाऱ्या इलेक्ट्रॉनांच्या उत्सर्जनाकरिता वरील क्रियावली गृहीत धरून उत्सर्जित विद्युत् प्रवाह घनता व उत्सर्जकाचे तापमान यांकरिता पुढील सूत्र काढता येते. या सूत्रास रिचर्ड्‌सन–दुशमान नियम असे म्हणतात.

J = A T² e ^–φ/kT

येथे J = तापायनिक विद्युत् प्रवाह घनता, T = उत्सर्जकाचे तापमान (^० के.), f = निव्वळ कार्यफलन, k = बोल्टस्‌मान स्थिरांक आणि e हा स्वाभाविक लॉगारिथमचा आधारांक आहे. वरील सूत्रात A हा स्थिरांक सर्वव्यापी म्हणजे सर्व उत्सर्जकांकरिता एकाच मूल्याचा (म्हणजे १२० अ‍ँपि./सेंमी.^२) एवढा असावा असे दाखविता येते. प्रत्यक्ष प्रयोगानुसार याचे मूल्य उत्सर्जकाच्या प्राकृतीक अवस्थेवर अवलंबून राहते, असे दिसून येते. या प्रयोगात १२० पेक्षा जास्त व १२० पेक्षा कमी अशी दोन्ही प्रकारची मूल्ये  A करिता मिळाली आहेत. बहुतेक सर्व मुख्य शुद्ध धातूंकरिता याचे मूल्य साधारणपणे ६० च्या आसपास आहे, असे दिसते. या तफावतीचे विशदीकरण करण्याकरिता खालील विविध कारणे सुचविली गेली आहेत : १) उत्सर्जकाच्या पृष्टभागाजवळ असलेल्या ‘वर्चस् तटा’ मुळे त्यापासून उत्सर्जित होणाऱ्या इलेक्ट्रॉनांचे अंशतः परावर्तन ही क्रिया रूढ परावर्तनासारखी नसून तिचे योग्य वर्णन पुंजयमिकीय सिद्धांतानुसारच द्यावे लागते. (२) एम्. एन्. निकल्झ (१९४०) व जी. एफ्. स्मिथ (१९५४) यांनी टंगस्टनाच्या एकसंघ स्फटिकाचा उत्सर्जक म्हणून उपयोग केला असता A आणि f या दोहोंचीही मूल्ये कोणत्या विशिष्ट प्रतलापासून उत्सर्जन झाले, यावर अवलंबून असताना असे दिसून आले. यापूर्वीचे बहुतेक सर्व प्रयोग ‘बहुस्फटिकी’ उत्सर्जक पृष्टभागावर झाले असल्यामुळे या प्रयोगान्ती A व f यांची सरासरी मूल्ये मिळाली असली पाहिजेत, हे उघड आहे. (३) कार्यफलन f हे तापमानावर अवलंबून असेल, तर त्यामुळे f या स्थिरांकाच्या कार्यकारी मूल्यावर परिणाम होऊ शकतो.

तापयानिक उत्सर्जनाचे हे सैद्धांतिक विवेचन सर्वमान्य झाले असून वरील तफावतीस विशेष महत्त्व दिले जात नाही. वरील विवेचन अर्धसंवाहक (ज्याची विद्युत् संवाहकता धातू व विद्युत् निरोधक यांच्या दरम्यान आहे अशा) पदार्थांपासून होणाऱ्या इलेक्ट्रॉनांच्या उत्सर्जनाला सुद्धा लागू पडते, असे मानले जाते.

शोट्‌की परिणाम : व्यवहारात उपयोगात असलेल्या काही तापायनिक उत्सर्जकांमध्ये (उदा., द्विप्रस्थ नलिका) उत्सर्जक विद्युत् प्रवाह संपृक्त होत नाही. पट्टिकेवरील विद्युत् दाब वाढविला असता या प्रवाहाचे मूल्य सारखे हळूहळू वाढत जाते, असे आढळते (आ. ३ मधील घच विभाग). याचे विश्लेषण व्हाल्टर शोट्‌की यांनी केले व त्यास आता शोट्‌की परिणाम असे म्हणतात. शोट्‌की यांच्या विवेचनाप्रमाणे पट्टिकेस लावलेले धन विद्युत् वर्चस् इलेक्ट्रॉन उत्सर्जनास अनुकुल असे विद्युत् क्षेत्र उत्सर्जकाच्या पृष्ठभागाजवळ निर्माण करते. यामुळे त्या जवळील वर्चस् तटाची कार्यकारी उंची कमी होऊन त्याच्या कार्यकारी कार्यफलनाचे मूल्य कमी होते. या परिस्थितीत मिळालेल्या विद्युत् प्रवाहाचे मूल्य निव्वळ उत्सर्जकाच्या तापमानावर अवलंबून न राहता पट्टिकेवर लावलेल्या वर्चसामुळे निर्माण झालेल्या F या विद्युत् क्षेत्रावरही अवलंबून असते. या परिणामकरिता शोट्‌की यांनी खालील सूत्र दिले आहे. 

J = A T² exp[f – e^3/2F^1/2]

या सूत्रात e = इलेक्ट्रॉन विद्युत् भार, F = विद्युत् क्षेत्र, exp = e या नैसर्गिक लॉगरिथमांच्या आधारांकाकरिता वापरलेले चिन्ह आहे [→ इ (e)]. 

ऑक्साइड पटलाचा परिणाम : ज्याप्रमाणे योग्य तऱ्हेने विद्युत् क्षेत्र लावले असता उत्सर्जकाचे कार्यकारी कार्यफलन कमी होऊन उत्सर्जनात वाढ होते, असाच परिणाम शुद्ध धातूच्या उत्सर्जकावर कॅल्शियम, स्ट्रॉंशियम व बेरियम यांसारख्या मूलद्रव्यांच्या ऑक्साइडांचा लेप दिला असता मिळतो. उत्सर्जकाच्या पृष्ठभागावर या अशुद्ध द्रव्याच्या रेणूंचा थर जमतो व परिणामतः मूळ धातूच्या कार्यफलनात लक्षणीय घट होते (कोष्टक पहा). अशा प्रकारच्या मिश्र उत्सर्जकाचा उल्लेख थोरियममिश्रित टंगस्टन अथवा ऑक्साइडलेपित निकेल असा आधीच करण्यात आला आहे.

विद्युत् क्षेत्र प्रेरित अथवा शीत उत्सर्जन : या प्रकारचे उत्सर्जन मिळविण्याकरिता उत्सर्जकाचे तापमान कोठी (परिसरीय) तापमानाएवढेच ठेवतात. त्याचे क्षेत्रफळ कमी करण्याकरिता तो बारीक तारेच्या स्वरूपात घेऊन त्याचे अग्र विशिष्ट क्रिया करून अत्यंत अणकुचीदार असे बनविले जाते. त्याच्याजवळ दुसरे एक अग्र प्रस्थापित करून ही सर्व रचना एका अत्यंत उच्च प्रतीच्या निर्वातामध्ये ठेवली जाते. दुसऱ्या अग्रावर विद्युत् वर्चस् लावून त्यामुळे उत्सर्जकाच्या पृष्ठभागाजवळ अत्यंत तीव्र असे विद्युत् क्षेत्र (≈ १०^७ व्होल्ट/सेमी.) निर्माण केले असता ऋणाग्रामधून इलेक्ट्रॉन उत्सर्जन मिळते, यास क्षेत्र प्रेरित अथवा शीत उत्सर्जन असे म्हणतात. तापायनिक उत्सर्जन ही बहुतांशी रूढ प्रकारची प्रक्रिया आहे.

हीमध्ये इलेक्ट्रॉन उत्सर्जक पृष्टभागाजवळील वर्चस् तट ओलांडून अवकाशात येतात. क्षेत्र प्रेरित उत्सर्जन ही क्रिया पुंजयामिकीनुसार वर्णन केलेल्या सुरंग परिणामाप्रमाणे होते [→ अर्धसंवाहक]. ही प्रक्रिया आधी वर्णिलेल्या क्रियेपेक्षा सर्वस्वी निराळी आहे. हीमध्ये क्षेत्र व विद्युत् प्रवाह यांमधील संबंध खालील सूत्राने मिळतो.

J = BF²e^-β/F

येथे F = विद्युत् क्षेत्र. B आणि β यांची मूल्ये वर्चस् तटाच्या आकारावर अवलंबून असतात. या प्रकारच्या उत्सर्जनाचा उपयोग ई. डब्ल्यू. म्यूलर यांनी १९३६ साली क्षेत्र उत्सर्जन सूक्ष्मदर्शक [→ इलेक्ट्रॉन सूक्ष्मदर्शक] बनविण्यात केला आहे. काही परिस्थितीत उत्सर्जकापासून इलेक्ट्रॉनाच्या ऐवजी आयन उत्सर्जन मिळविता येते. या परिणामाचा उपयोग म्यूलर यांनी क्षेत्र आयन सूक्ष्मदर्शक तयार करण्यासाठी केला.

शॉट गोंगाट : संदेशवहनामध्ये वापरल्या जाणाऱ्या प्रयुक्ती व उपकरणे यांमध्ये काही अनिष्ट संदेश कमीजास्त प्रमाणात उत्पन्न होत असतात. यांच्यामुळे सामान्यतः इष्ट संदेशात काही प्रमाणात विक्षेप होतात व त्यामुळे परिणामतः त्या साधनाची उपयुक्तता कमी होते. अशा अवांतर संदेशास गोंगाट म्हणतात (याचा अनुभव दूरध्वनी संदेशग्रहणात अनेक वेळा येतो). तापायनिक उत्सर्जनामध्ये गोंगाट खालील कारणामुळे निर्माण होतो. उत्सर्जकापासून निघणाऱ्या इलेक्ट्रॉनांच्या संख्येत आणि गतीत सतत अनियत बदल होत असल्यामुळे कोणत्याही द्विप्रस्थ इ. नलिकांच्या पट्टिका प्रवाहात या कारणामुळे सतत कालावर्ती बदल होत जातो. सैद्धांतिक दृष्ट्या अशा प्रकारचा विद्युत् प्रवाह म्हणजे एका स्थिर मूल्य असलेल्या विद्युत् प्रवाहाबरोबर एक प्रत्यावर्ती (उलटसुलट दिशेने वाहणारा) विद्युत् प्रवाह अध्यारोपित केला गेला आहे, असे समजता येते. हा प्रत्यावर्ती घटक म्हणजेच गोंगाट होय. इलेक्ट्रॉनीय नलिका पर्यावेश–निर्धारित अवस्थेत वापरली असता या गोंगाटाचे प्रमाण कमी करता येते.

‘लुकलुक’ (फ्लिकर) गोंगाट :वर वर्णन केलेला शॉट गोंगाट सर्वांत जास्त प्रकर्षाने तापमान–निर्धारित विद्युत् प्रवाहात आढळून येतो. मागे नमूद केल्याप्रमाणे संपृक्त विद्युत् प्रवाह हा शुद्ध धातूच्या उत्सर्जकाच्या याच विभागात मिळतो. उत्सर्जक जर ऑक्साइडलेपित असेल, तर त्यापासून जास्त उत्सर्जनक्षमता मिळते हे खरे पण त्याबरोबरच त्याच्यामधून आणखी एक निराळ्या प्रकारचा गोंगाट निर्माण होतो, यास ‘लुकलुक’ गोंगाट अशी संज्ञा दिली आहे. उत्सर्जकाच्या निरनिराळ्या भागांतून होणाऱ्या उत्सर्जनाच्या प्रमाणातील बदलामुळे हा परिणाम निर्माण होतो. यामुळे पट्टिका विद्युत् प्रवाहात होणारे बदल मंदगती असल्यामुळे या गोंगाटापासून होणारे दुष्परिणाम तितके गंभीर स्वरूपाचे नसतात.

पहा : इलेक्ट्रॉनीय प्रयुक्ति. 

संदर्भ : 1. Hemenway, C. L. Henry, F. W. Caulton, M. Physical Electronics, New York, 1967.

   2. Kloeffler, R. G. Industrial Electronics and Control, New York, 1963.

   3. Parkar, P. Electronics, London, 1963.

   4. Richardson, O. W. Emission of Electrons from Hot Bodies, London, 1912. 

   5. Spangenberg, K. R. Vacuum Tubes, New York, 1948.

बापट, अ. वा. चिपळोणकर, व. त्रि.

“