नियंत्रण प्रणाली : नियंत्रण प्रणालीच्या साहाय्याने कोणत्याही एका (किंवा अनेक) भौतिक चल (बदलत्या) राशीचे नियंत्रण केले जाते. नियंत्रित चल राशींमध्ये (१) द्रायूचा (वायूचा वा द्रवाचा) दाब, (२) तापमान, (३) विद्युत् दिव्याची तेजस्विता, (४) तोफेचा यामिकीय दिक्विन्यास (भौतिक प्रेरणांनी योग्य दिशेत वळविणे), (५) परिभ्रमी चाकाचा कोनीय वेग, (६) कोणत्याही वस्तूचे स्थान यांसारख्या राशींचा समावेश होतो. ज्या प्रणालींच्या साहाय्याने अवकाशातील स्थान अथवा ठिकाण निश्चित केले जाते अशांना ⇨ सेवायंत्रणा (सर्व्होमेकॅनिझम) अशी संज्ञा सर्वसाधारणपणे वापरण्यात येते. दूरवर्ती नियंत्रित विमानाचे स्थान किंवा तोफेचा यामिकीय दिक्विन्यास करण्याकरिता सेवा-यंत्रणा वापरल्या जातात. ज्या विशिष्ट प्रणालीचा उपयोग एखाद्या चल राशीचे मूल्य कालानुसार स्थिर ठेवण्याकरिता होतो त्यास नियामक प्रणाली असे म्हणतात. विद्युत् पुरवठ्यात होणाऱ्या आकस्मित बदलापासून शीत कपाट (रेफ्रिजरेटर) आणि दूरचित्रवाणी ग्राहीचे संरक्षण करण्याकरिता विद्युत् दाब स्थिर ठेवणारा नियामक वापरतात. विविध नियंत्रण प्रणालींचे कार्य परिस्थितीच्या अनुषंगाने निरनिराळ्या प्रकारे होते.
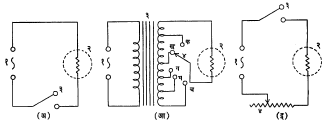
यांपैकी काही प्रातिनिधिक प्रणालींचे वर्णन खाली केले आहे. विजेच्या दिव्याची तेजस्विता ‘चालू-बंद’ नियंत्रण करण्याकरिता लागणारी योजना आ.१ (अ) मध्ये दाखविली आहे. या योजनेत आज्ञेनुसार स्विच (३) योग्य स्थितीत आणून दिवा चालू किंवा बंद करता येतो. यामध्ये दिव्याची तेजस्विता शून्य व एक ठराविक स्थिर मूल्य या दोहोंपैकी एक मूल्यच धारण करू शकते. आ. १ (आ) मधील योजनेत एक रोहित्र (विद्युत् दाब बदलणारे साधन) वापरले आहे. याच्या द्वितीयक वेटोळ्याला अनेक ठिकाणी जोड देऊन पर्यायी फाटे ठेवले आहेत. घूर्णी (फिरत्या) स्पर्शकाचा (४) स्पर्श क, ख, ग, घ, च यांपैकी योग्य त्या अग्रास करून दिव्याची तेजस्विता शून्य व महत्तम किंवा यांमधील आणखी तीन टप्प्यांत बदलता येते. आ.१ (इ) मध्ये दाखवेलल्या योजनेत चल रोधकावरील स्पर्शकाचे स्थान बदलून दिव्याची तेजस्विता दोन मर्यादामूल्यांमध्ये अखंडितपणे बदलता येते. आ.१ (अ) आणि (आ) मधील नियंत्रण प्रणाली नैकरेषीय [→ नैकरेषीय आविष्कार] आहेत असे दाखविता येते, तर आ.१ (इ) मधील प्रणालीचे कार्य रेषीय किंवा नैकरेषीय प्रकारचे असू शकेल असे दिसते. प्रणाली रेषीय किंवा नैकरेषीय रीत्या कार्य करते हे तिच्या कार्याचे वर्णन करण्याच्या ⇨ अवकल समीकरणावरून ठरविले जाते. याबद्दलच्या स्पष्टीकरणाकरिता पुढील मजकूर पहावा.
अपूर्ण-वलय व संवृत-वलय प्रणाली : वरील सर्व प्रणाली प्रकांरामध्ये नियंत्रण केल्यानंतर प्रत्यक्षात दिव्याची तेजस्विता (ज्यास नियंत्रित राशी किंवा प्रणाली परिणाम अथवा प्रदान म्हणतात) काय मिळते, याचा विचार करून अनुयोजन केलेले नसते. काही बाह्य कारणामुळे सुद्धा दिव्याच्या तेजस्वितेत बदल होण्याचा संभव नेहमीच असतो. उदा.,जर विद्युत् पुरवठ्याचा दाब कमीजास्त झाला, तर त्यामुळे दिव्याची तेजस्विता कमीजास्त होऊ शकेल. या गोष्टीचे निरीक्षण करून त्याप्रमाणे नियंत्रण कार्यामध्ये या प्रणालीत फेरफार केले जात नाहीत म्हणून या प्रकारच्या नियंत्रण प्रणालीस अपूर्ण-वलय नियंत्रण प्रणाली असे म्हणतात. याउलट शीत कपाटातील तापस्थापक (तापमान स्थिर ठेवणाऱ्या) नियंत्रण प्रणालीचे कार्य निराळ्या रीतीने घडते. आधी ठरवून दिलेल्या पातळीपेक्षा शीत कपाटातील तापमान वाढले, तर नियंत्रण योजना कार्यान्वित होऊन त्यामधील संपीडकाचे (वायूचा दाब वाढविणाऱ्या साधनाचे) विद्युत् चलित्र (मोटर) सुरू केले जाते. यामुळे आतील तापमान कमी होऊ लागते व त्याची किमान पातळी एका ठराविक मूल्यापर्यंत आली की, नियंत्रण योजना परत कार्यान्वित होऊन विद्युत् चलित्राचा स्विच बंद करते. ही नियंत्रण योजनासुद्धा बऱ्याच प्रमाणात चालू-बंद प्रकाराची (म्हणजे नैकरेषीय स्वरूपाची) आहे. यामध्ये शीत कपाटातील तापमान ही नियंत्रित राशी आहे व या राशीचे प्रत्यक्ष मूल्य काय आहे (हे मापन करून) हे विचारात घेऊन ही प्रणाली कार्य करते. मिळालेल्या परिणामाचे (म्हणजे तापमानाचे) या प्रणालीत ज्ञान करून घेऊन व त्याचा पुन:प्रदाय क्रियेद्वारे (प्रणालीच्या प्रदानाचा काही भाग पुन्हा आदानाला देण्याच्या क्रियेद्वारे) उपयोग करून घेऊन त्याप्रमाणे योग्य असे नियंत्रण कार्य होत असल्यामुळे या प्रणालीस संवृत-वलय प्रणाली अशी संज्ञा दिली जाते. संवृत-वलय प्रणालीचे आणखी एक सर्वसाधारणपणे आढळणारे उदाहरण म्हणजे तरत्या गोळ्याच्या झडपेची पाण्याच्या टाकीत वापरलेली योजना ही होय. यामध्ये तांब्याचा (किंवा प्लॅस्टिकचा) एक पोकळ गोळा (फुगा) एक दांड्याच्या टोकाशी बसविलेला असतो. दांड्याच्या दुसऱ्या टोकास दट्ट्या जोडलेला असतो. ज्या नळीमधून टाकीला पाण्याचा पुरवठा होत असतो त्याच्या टोकाशी हा दट्ट्या बसविलेला असतो. जेव्हा टाकीत पाणी नसते तेव्हा तीतील गोळा सगळ्यात खालच्या पातळीवर असतो. या स्थितीत दुसऱ्या टोकाशी बसविलेल्या दट्ट्या येणाऱ्या पाण्याच्या प्रवाहास सर्वांत कमी रोध करतो. या स्थितीत पाण्याच्या प्रवाहाची त्वरा महत्तम असते. टाकीत पाणी पडून तिच्यातील पाण्याची पातळी जसजशी वाढत जाते तसतसा हा गोळा हळूहळू वर ढकलला जातो. पाण्याच्या पातळीने एक ठराविक मर्यादा गाठली की, हा गोळा सर्वांत वरच्या स्थानी जातो. या स्थितीत दट्ट्या नळीतून पडणाऱ्या पाण्यास संपूर्ण रोध करून पाण्याचा प्रवाह संपूर्णपणे बंद करतो. या प्रणालीचे वर्णन ‘चालू-बंद’ असे ढोबळमानाने करता आले, तरी पाण्याचा प्रवाह चालू आणि पूर्णपणे बंद या दोन अवस्थांच्या मधल्या स्थितीत नियंत्रण चालूच असते व प्रवाहाची त्वरा सारखी कमी होत असते, हे लक्षात घेण्याजोगे आहे. ही प्रणाली ऐतिहासिक दृष्ट्या सर्वांत जुनी असे मानले जाते कारण अशाच प्रकारची योजना प्राचीन काळी रोमन लोक वापरीत होते, असा पुरावा उपलब्ध आहे.
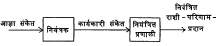
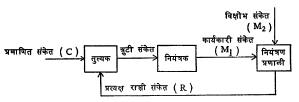
आ. २ व ३ यांवरून अपूर्ण-वलय व संवृत-वलय नियंत्रण प्रणालीमधील फरक स्पष्ट होईल. अपूर्ण-वलय नियंत्रण प्रणालींमधील फरक स्पष्ट होईल. अपूर्ण-वलय नियंत्रण प्रणालीत आज्ञा संकेतानुसार नियंत्रकामध्ये योग्य असा कार्यकारी संकेत निर्माण केला जातो. या संकेतामुळे नियंत्रित प्रणालीमध्ये योग्य असा बदल घडवून आणण्यात येतो. त्यामुळे शेवटी अपेक्षित अथवा इष्ट परिणाम मिळतो. आ.१ (अ) मध्ये वर्णन केलेल्या प्रणालीत विजेचा दिवा चालू किंवा बंद करणे या आज्ञा संकेतानुसार प्रचालक व्यक्ती आपल्या हाताच्या साहाय्याने कार्यकारी प्रेरणा संदेश वापरून, स्विच योग्य दिशेने हालवून इष्ट परिणाम घडवून आणतो. वरील पद्धतीत बदलक्रम एकामागून एक असा असतो आणि त्यांची शृंखला अपूर्ण-वलयाच्या स्वरूपात असते. यावरून या प्रणालीस अपूर्ण-वलय नियंत्रण प्रणाली का म्हणतात हे स्पष्ट होते. संवृत-वलय प्रणालीचा आराखडा आ. ३ मध्ये दाखविला आहे. नियंत्रित प्रणालीमधून परिणामी मिळणाऱ्या नियंत्रित राशीचे
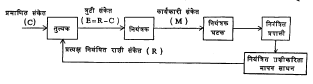मापन, मापकसाधनाच्या साहाय्याने करून त्यापासून मिळणाऱ्या (R) संकेताचे मूळ प्रमाणित संकेत (C) याच्याशी तुल्यकाद्वारे तुलना करून त्यामधील फरकाच्या प्रमाणात त्रुटी संकेत (E) मिळतो. प्रमाणित संकेत (C) मूळ आज्ञा संकेताने निश्चित केलेला असतो. त्रुटी संकेत नियंत्रकाला मिळाल्यानंतर त्यापासून कार्यकारी संकेत (M) हा मिळतो. नियंत्रकामध्ये विवर्धन योजना वापरून त्रुटी संकेताचे विवर्धन करून त्याची शक्ती पातळी योग्य मर्यादेपर्यंत वाढविली जाते. कार्यकारी संकेत (M) कार्यकारी घटकाच्याद्वारे नियंत्रित प्रणालीवर कार्य करून त्यामधील प्रदानामध्ये योग्य तो प्रत्यक्ष बदल घडवून आणतो. कित्येक आराखड्यांमध्ये नियंत्रक घटक निराळा दाखवीत नाहीत. त्याचे प्रणालीतील अस्तित्व गृहीत धरले जाते. परिणाम हा C मध्ये घडून येणारा बदल त्रुटी संकेताचे मूल्य कमी करील असा असला पाहिजे, हे उघड आहे. दुसऱ्या पद्धतीच्या नियंत्रण प्रणालीमधील विविध टप्प्यांचे वर्णन जे वर केले त्यावरून हे लक्षात येईल. यामधील प्रत्येक टप्पा कार्यान्वित करण्याकरिता काहीतरी ठराविक कालावधी लागणार. मापक साधनाच्या द्वारे मापन व त्याची प्रमाणित संकेताबरोबर राशीची तुलना करण्याकरिता काही काल लागणार, तर त्रुटी संकेत नियंत्रकाला मिळाल्यापासून कार्यकारी संकेतनिर्मितीला सुद्धा काही काल लागणार. त्यामुळे त्रुटिमापन व नियंत्रण प्रणालीद्वारे शेवटी प्रतिपूरण यांमध्ये एक ठराविक कालविलंब होत असणार. प्रणालीचा प्रत्यक्ष अभ्यास करून असे आढळते की, या एकंदर कालविलंबामध्ये काही भाग क्रियाशून्य काल असतो, तर काही भाग निरनिराळ्या विभांगाच्या कालस्थिरांकामुळे ठरविला जातो. संपूर्ण कालविलंबाचे मापन करण्याकरिता (प्रणालीचा पुन:प्रदाय विभाग अलग करून) आ. ३ मध्ये प्रमाणित संकेताच्या ठिकाणी पायरी फलन म्हणजे आ. ४ मध्ये दाखविल्याप्रमाणे कालानुसार बदलणारे आदान (त्रुटी) दिली जाते.
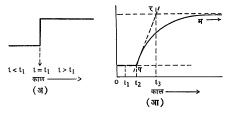
त्यापासून मिळणाऱ्या प्रदानात कालानुसार होणारा बदल मोजला जातो. लावलेल्या आदान पायरी फलनाचे स्वरूप आ. ४ (अ) मध्ये दाखविले आहे, तर हे आदान प्रणालीला दिले असता त्यापासून मिळणाऱ्या प्रदानाचे स्वरूप (पम) आ. ४ (आ) मध्ये दाखविले आहे. काल t = t1 या क्षणी आदान दिले जात असल्यामुळे t1 ते t2 मधील काल हा क्रियाशून्य कालावधी आहे, हे उघड आहे. प्रतिसाद वक्राच्या ज्या बिंदूपासून (प) चढ महत्तम होतो, त्या बिंदूपासून एक स्पर्शरेषा काढली जाते. दुसरी रेषा क्ष-अक्षापासून प्रदानाच्या अंतिम मूल्याएवढ्या अंतरावर व तिला समांतर अशी काढतात. या दोन रेषा जेथे एकमेकींस छेदतात त्या बिंदूपासून (र) क्ष-अक्षावर एक लंब काढतात. दुसरा लंब प या बिंदूतून काढतात. t2 ते t3 हा कालावधी प्रणालीचा कालस्थिरांक दाखवितो. ज्या गतिकी अवकल समीकरणानुसार नियंत्रण प्रणाली कार्य करते ते जर अचूक रीत्या माहीत असेल, तर गणितीय रीत्या प्रणालीच्या कालस्थिरांकाचे मूल्य कसे काढता येते, हे पुढे दाखविले आहे. कालपरिवर्ती (कालानुसार बदलणारी) त्रुटी असताना प्रणालीच्या प्रतिसादाचे विवेचन करण्याकरिता हे दोन कालावधी कसे महत्त्वाचे ठरतात, हे पुढे विशद केले आहे.
ऐतिहासिक : पुन:प्रदाय नियंत्रण प्रणालींचा उपयोग मानवाने गेल्या काही सहस्त्र वर्षांपासून केला आहे तरत्या गोळ्याच्या झडपेने पाण्याच्या प्रवाहाचे नियंत्रण करण्याची योजना रोमन लोकांनी प्राचीन काळी केली असल्याचा उल्लेख मागे आलाच आहे. वाफ एंजिनाचा वेग नियंत्रित करण्याकरिता जेम्स वॉट यांनी योजलेला ⇨ गतिनियंता (गव्हर्नर) हा याच प्रकारच्या नियंत्रकाचे महत्त्वाचे उदाहरण होय. १९१९ साली एन्. मिनॉर्स्की यांनी लढाऊ जहाजाचे डोलणे कमी करण्यासाठी पुन:प्रदाय योजना प्रथम वापरली. १९३० च्या सुमारास पुन:प्रदाय नियंत्रण पद्धतीचा उपयोग रासायनिक प्रक्रिया संयंत्रात (यंत्रसंचात) व खनिज तेलाच्या परिष्करण कारखान्यात उत्पादनाची गुणवत्ता व संयंत्राची उत्पादनक्षमता यांच्या नियंत्रणासाठी करण्यात आला. आधुनिक नियंत्रण प्रणालींचा सांगोपांग पद्धतशीर अभ्यास करण्यासाठी रशियामध्ये एक स्वतंत्र संस्था स्थापन करण्यात आली. त्यानंतर थोड्याच काळात अशाच तऱ्हेची संस्था अमेरिकेच्या संयुक्त संस्थानांतील मॅसॅचूसेट्स इन्स्टिट्यूट ऑफ टेक्नॉलॉजी येथे स्थापण्यात आली. दुसऱ्या महायुद्धाच्या काळापासून तोफांचा दिक्विन्यास, क्षेपणास्त्रांचे मार्गदर्शन यांसारख्या कार्यांकरिता लागणाऱ्या नियंत्रण प्रणालीचे गणितीय विश्लेषण व अभिकल्पन (आराखडा तयार करणे) करण्याकडे विशेष लक्ष देण्यात येऊ लागले. संगणकांचा (गणितीय कृत्ये करणाऱ्या यंत्रांचा) उपयोग या विशिष्ट कार्याकरिता विशेष मोठ्या प्रमाणावर होऊ लागला.
मानवी व स्वयंचलित नियंत्रण प्रणाली : आ. १ मध्ये विजेच्या दिव्याची तेजस्विता नियंत्रित करण्याकरिता ज्या प्रणालीचे वर्णन करण्यात आले आहे तीमध्ये प्रत्यक्ष नियंत्रण कार्याकरिता मनुष्याची आवश्यकता लागेल, हे स्पष्ट आहे. याउलट शीतकपाटातील तापमानाचे किंवा टाकीतील पाण्याच्या प्रवाहाच्या त्वरेचे नियंत्रण करण्याकरिता वर्णन केलेल्या योजना मानवरहित असल्यामुळे त्यांस स्वयंचलित प्रणाली असे म्हणतात. तसे पाहिले असता मनुष्याचा व इतर प्राण्यांच्या शरीरांत असंख्य नियंत्रण प्रणाली आहेत. मनुष्याच्या शरीराचे तापमान स्थिर ठेवणारी यंत्रणा किंवा त्याच्या हातापायाच्या हालचाली नियंत्रित करण्याच्या योजना या नियंत्रण प्रणालीच होत.
मानवाने कार्यान्वित केलेल्या प्रणालीत व स्वयंचलित प्रणालित तसा तत्त्वत: फरक नाही, हे खालील विवेचनावरून स्पष्ट होईल. एखाद्या हुशार नोकराने मालकाच्या आज्ञेनुसार केलेले काम हे संवृत्त-वलय प्रणालीचे एक उदाहरण होय. मालकाच्या आज्ञेबरहुकूम काम करण्याकरिता नोकराजवळ (१) आवश्यक बल, (२) कौशल्य व (३) प्रत्यक्षात काम कसे होत आहे व ते आज्ञेप्रमाणे होते आहे की नाही जाणण्याची पात्रता असणे आवश्यक आहे. कारण जर प्रत्यक्ष कार्य मूळ आज्ञेप्रमाणे होत नसेल, तर त्यास कार्यपद्धतीमध्ये आवश्यक तो बदल करता आला पाहिजे. यांपैकी (२) आणि (३) या गोष्टी पुन:प्रदाय क्रियेमुळे मिळणाऱ्या ज्ञानावरच अवलंबून असतात. एखाद्या अकुशल नोकराने चालविलेला उद्वाहक (लिफ्ट) व स्वयंचलित उद्वाहक यांच्या कार्याची तुलना केल्यास हा मुद्दा स्पष्ट होतो. अकुशल नोकराने चालविलेला उद्वाहक काही वेळा चुकीच्या जागी थांबतो आणि त्याची गती स्थिर नसून तो गतिमान असताना धक्के बसतात. स्वयंचलित उद्‌वाहकमध्ये हे दोष नसतात. कारण त्याच्या नियंत्रण प्रणालीस काय होत आहे याचे जास्त अचूक ज्ञान असते. उद्‌वाहकाची स्थिती व गती यांविषयी ज्ञान करून घेण्याकरिता यामध्ये संवेदक उपकरणे असतात, त्यायोगे हे कौशल्य त्यास प्राप्त होते. यावरून प्रणालीचे कौशल्य तीमध्ये नियंत्रित राशीचे निरीक्षण आणि मापन करण्याकरिता वापरलेल्या प्रयुक्तीच्या अचूकतेवर अवलंबून असते, हे लक्षात येते.
कार्यकारी प्रेरणेच्या (M) निर्मितीकरिता एक स्थानिक ऊर्जा उद्‌गम असणे आवश्यक असते आणि ऊर्जा स्थानांतरणाचे नियंत्रण करण्याकरिता एक साधनही लागते, हे येथे नमूद केले पाहिजे. विद्युत् दिव्याच्या नियंत्रण प्रणालीचे जे उदाहरण वर घेतले होते त्याच्या अनुषंगाने या दोन गोष्टींचे विवेचन करता येते. आ. १ (अ) मध्ये स्विच चालू किंवा बंद करण्याकरिता किंवा आ. १ (इ) मध्ये चलरोधकावरील स्पर्शक हलविण्याकरिता लागणारी ऊर्जा प्रचालक मनुष्याच्या हाताच्या स्नायूंपासून मिळते. या प्रणालीत या ऊर्जेमुळे विद्युत् ऊर्जेच्या स्थानांतरणाचे नियंत्रण होते. काही वेळा मात्र या दोन ऊर्जा उद्‌गमांत फरक असत नाही. उदा., सायकल चालविणारा माणूस. या उदाहरणामध्ये सायकलीच्या गतीची दिशा ही नियंत्रित राशी आहे व तिचे नियंत्रण सायकलीवर बसलेला मनुष्य हँडलची दिशा बदलून करतो. याकरिता लागणारी ऊर्जा त्याच्या हाताच्या स्नायूंपासून मिळते, तर सायकलीला गती देण्याकरिता लागणारी ऊर्जा त्याच्या पायांच्या स्नांयूपासून मिळते. ज्या प्रणालीमध्ये नियंत्रण करण्याकरिता लागणारी ऊर्जा (A) ही नियंत्रित ऊर्जेपेक्षा (B) कमी असते. अशा परिस्थीतीत (A < < B) कार्यशक्तीचे विवर्धन होते असे म्हणतात.
स्वयंचलित एकक धारणक्षमतेची रेषीय प्रणाली : स्वयंचलित नियंत्रण प्रणालीचे विवेचन करणे गणितीय दृष्ट्या सुलभ व सुस्पष्ट असते. एकक धारणक्षमता असलेल्या रेषीय प्रणालीचे गणितीय विश्लेषण करणे तर सगळ्यांत सुलभ व समजावयास सोपे ठरते. एकक धारणक्षमता प्रणालीतील संपूर्ण ऊर्जा एकाच प्रकारच्या संचयात साठविलेली असते वा तिचे मूल्य एका राशीवरच अवलंबून असते आणि हीच राशी प्रणालीद्वारे नियंत्रित केली गेलेली असते. या विशिष्ट प्रकारच्या प्रणालीचे वर्णन प्रथम कोटीच्या रेषीय (एकघाती) अवकल समीकरणाद्वारे करता येते. या प्रकारच्या प्रणालीत त्रुटी संकेताच्या परिणामाचे मूल्य काढण्याकरिता अध्यारोपण तत्त्व मानता येते. त्रुटी संकेत व कार्यकारी संकेत यांमधील संबंध रेषीय स्वरूपाचा असेल, तर हे शक्य होईल, हे स्पष्ट आहे. या प्रणालीची खालील दोन साधी उदाहरणे आहेत. (१) श्यान-संदमित परिभ्रमी चक्र : यामध्ये श्यान (दाट) द्रवात बुडविलेले दंडगोलाकार चक्र असते (या श्यान द्रवामुळे चक्राच्या गतीचे संदमन–कमी होणे–होते). त्याच्या एका बाजूस चालक परिपीडन (परिभ्रमी गती देणारी प्रेरणा व तिचे परिभ्रमण अक्षापासूनचे अंतर यांच्या गुणाकाराने मिळणारी राशी) व दुसऱ्या बाजूस परिपीडन भार असतो. या योजनेत चाकाची कोनीय गती ही नियंत्रित राशी असून प्रणालीची ऊर्जा कोनीय गतीच्या मूल्यानेच निश्चित होते. (२) एका बंदिस्त भांड्यात ठेवलेल्या द्रवाचे तापमान त्यात बुडवून ठेवलेल्या संवाहक तारेच्या वेटोळ्यात योग्य विद्युत् प्रवाह काही ठराविक कालापर्यंत सोडून इष्ट मूल्यावर नेता येईल आणि द्रवाचे तापमान सर्वत्र सारखे रहावे याकरिता ते सारखे ढवळले जाईल अशी योजना केली व परिसराचा त्यावर परिणाम होऊ नये याकरिता द्रवाभोवती ऊष्मीय निरोधकाचे आवरण ठेवले, तर या विशिष्ट प्रणालीमधील ऊर्जा त्याच्या तापमानावरच अवलंबून राहील असे दाखविता येते व अशा प्रणालीचे नियंत्रण करणारे गतिकी अवकल समीकरण प्रथम कोटी रेषीय स्वरूपाचेच असते असे आढळून येते. गणितीय विवेचनाच्या सोयीकरिता यापुढील बहुतेक सर्व विश्लेषण याच प्रकारच्या प्रणालीच्या अनुषंगाने करण्यात आले आहे.
एकक धारणक्षमतेच्या रेषीय संवृत-वलय प्रणालीचे कार्य : वरील पद्धतीच्या नियंत्रण प्रणालीमध्ये काही गुणधर्म आवश्यक आहेत असे दाखविता येते. श्यान-संदमित परिभ्रमी चक्राचे उदाहरण घेतल्यास त्याच्या इष्ट राशीत कोनीय वेगात होणारे बदल दोन प्रकारचे असू शकतात. वरील चक्राच्या भारात काही कारणामुळे फरक झाल्यास चक्राच्या कोनीय वेगात बदल होऊ शकतो, तर दुसऱ्या तऱ्हेचा बदल प्रणालीला बाहेरून मिळालेल्या एखाद्या विक्षोभामुळे होऊ शकतो. पहिल्या प्रकारचा बदल कायम स्वरूपाचा असू शकतो, तर दुसऱ्या प्रकारचा बदल सर्वसाधारणपणे कालपरिवर्ती किंवा अस्थायी असू शकतो. प्रणालीची कार्यक्षमता उच्च असावी असे अपेक्षित असल्यास या दोन्ही कारणांमुळे उत्पन्न होणाऱ्या त्रुटीचे प्रमाण कमी असावे व त्याकरिता प्रणालीच्या प्रतिसादाची त्वरा उच्च असावी, असे कळते. या अपेक्षा निश्चित करण्याकरिता प्रणालीस खालील अटी पाळाव्या लागतात. (१) चाकावरील भार शून्यापासून महत्तम मूल्यापर्यंत वाढवित नेल्यास त्यामुळे परिणामी कोनीय वेगात होणारा स्थिर-स्थिती अथवा कायम बदल १० टक्क्यांहून जास्त नसावा. (२) कालपरिवर्ती विक्षोभामुळे मिळणारा त्रुटी संकेत व त्यापासून मिळणारा कार्यकारी संकेत या दोहोंस स्थिर-स्थिती मूल्य धारण करण्यास लागणारा कालावधी अल्प असावा. (३) कार्यकारी संकेताने होणाऱ्या बदलामुळे प्रणालीत आंदोलने निर्माण होत नाहीत व तिचे स्थैर्य बिघडत नाही, हे सुद्धा बघणे आवश्यक ठरते.
या सर्व अटी पूर्ण करण्याकरिता प्रणालीचे अभिकल्पन कसे करावे या विषयीची कल्पना खाली दिलेल्या नियंत्रण प्रणालीच्या ढोबळ गणितीय विश्लेषणापासून मिळते. त्रुटी संकेत E = R–C यामुळे नियंत्रकामधून M1 कार्यकारी संकेत मिळत असेल, तर M1 = H (R–C) …… ………………………..…(१)
येथे H याला नियंत्रक स्थानांतरण फलन म्हणतात. M1 व E यांमधील चलन रेषीय आहे असे मानले आहे. जर याच वेळी प्रणालीस M2 हा विक्षोभ संकेत मिळाला, तर त्यामुळे प्रदान राशी G2M2 एवढी मिळेल. विक्षोभ संकेताकरिता नियंत्रण प्रणालीचे स्थानांतरण फलन G2 असे मानले, तर M1 या संकेताकरिता हे फलन G1 एवढे आहे, असे गृहीत धरले आहे. प्रणालीचे कार्य रेषीय आहे असे मानल्यामुळे परिणामी प्रदान राशीचे मूल्य खालील समीकरणाने मिळते.
जर HG1 > > 1 आणि HG1 >> G2 या अटी पूर्ण झाल्या, तर प्रदान राशी व प्रमाणित राशी एकरूप होतात (कारण E = 0) व विक्षोभाचा प्रणालीवर होणारा परिणाम नगण्य असतो असे दिसते. वरील अटी पूर्ण करण्याकरिता प्रणालीचा लाभांक (प्रदान व आदान यांचे गुणोत्तर) खूप मोठा केला पाहिजे, हे उघड आहे. लाभांक फार मोठ्या प्रमाणात वाढविला, तर त्यामुळे प्रणालीत अस्थैर्य निर्माण होते व प्रणालीच्या अस्थायी प्रतिसादाचा प्रतिकूल परिणाम होतो. याचा विचार पुढील भागात केला आहे.
एकक धारणक्षमतेच्या रेषीय प्रणालीचा अस्थायी प्रतिसाद : संवृत-वलय प्रणालीच्या प्रतिसादाचा अभ्यास करण्याकरिता प्रथम त्या प्रणालीमधून पुन:प्रदाय योजना काढून टाकली आहे असे मानू. याकरिता मानलेली प्रतिकृती पूर्वीचीच आहे. श्यान माध्यमात एका परिभ्रमी चक्राच्या अक्षाच्या एका टोकीस परिपीडन भार ML आहे, तर दुसऱ्या टोकास M हे चालक परिपीडन आहे असे समजले आहे. चक्राच्या गतीकरिता खालील अवकल समीकरण मिळते.
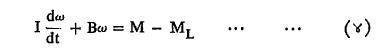
येथे І परिभ्रमण अक्षाभोवती चाकाचे निरूढी परिबल (कोनीय प्रवेगाला केलेला विरोध), ω कोनीय वेग, Bω संदमक परिपीडन, B संदमक स्थिरांक, (M – ML) परिणामी परिपीडनाचे मूल्य. वरील परिस्थितीत प्रणालीवर नियंत्रण नसून त्यामध्ये पुन:प्रदाय योजनाही नाही, हे नमूद केले पाहिजे.
या प्रणालीचा कालपरिवर्ती प्रतिसाद काढण्याकरिता (M – ML) चे मूल्य शून्यापासून (M – ML)0 या मूल्यापर्यंत एकदम (म्हणजे पायरी फलन स्वरूपात) वाढविले, तर गणितीय रीतीने तात्कालिक कोनीय वेग (ω) पुढील सूत्राने मिळतो.
याप्रमाणे t कालानुसार वाढत जातो असे दाखविता येते. या पदावलीमध्ये τ प्रणालीचा कालस्थिरांक (= І/B) आहे व e हा नैसर्गिक लॉगरिथमचा आधारांक आहे (⟶ इ.) कालस्थिरांकाच्या मूल्यावरून प्रणालीच्या कालपरिवर्ती प्रतिसादाविषयी कल्पना करता येते कारण कोनीय वेगात बदल घडवून आणणारी घटना सुरू केल्याच्या क्षणापासून, नवीन कोनीय वेगाने ९८% इतके मूल्य धारण करण्याकरिता प्रणालीस अंदाजे ४ τ एवढा कालावधी लागतो. या कालानंतर चाकाचा वेग ω* हे स्थिर मूल्य धारण करतो असे समजू.
या स्थितीत पुन:प्रदाय योजना नियंत्रण प्रणालीस जोडली जाते असे मानू. ω* हाच इष्ट कोनीय वेग आहे असे समजले, तर या स्थितीत त्रुटी संकेत शून्य असून नियंत्रण प्रणालीद्वारे मिळणारा कार्यकारी संकेतही शून्य मूल्याचाच असेल. या परिस्थितीत भार आणि श्यान क्रियेमुळे होणारे संदमक परिपीडन व चालक परिपीडन यांमध्ये समतोल निर्माण होतो आणि अंती त्यामुळे कोनीय वेग स्थिर राहतो, असे वर्णन करता येते. या परिस्थितीत
Bω*= (M – ML)0 … … … (६)
आता जर ML मध्ये एक पायरी फलन प्रकारचा बदल घडवून ML चे मूल्य ML + Δ ML एवढे केले, तर त्यामुळे कोनीय वेग ω* पासून ω हे मूल्य धारण करील.
पुन:प्रदाय नियंत्रण प्रणालीमुळे कार्यकारी संकेतात HE एवढा बदल होतो. समीकरण (४), (६) व (७) यांचा उपयोग केला असता,
सेमी. (५) आणि (९) यांची तुलना केल्यास नियंत्रित व अनियंत्रित प्रणालींमध्ये एकाच प्रकारची म्हणजे धातांकीय स्वरूपाची कालानुसार वाढ मिळते असे दिसून येते. नियंत्रित प्रणालीत कालस्थिरांक कमी मूल्याचा असतो व त्यामुळे नियंत्रित राशीला स्थिर-स्थिती मूल्य धारण करण्यास कमी वेळ लागतो हेही समजते.
स्थिर-स्थिती त्रुटी मूल्य : प्रणालीत केलेल्या बदलाचा अस्थायी परिणाम नाहीसा झाल्यानंतर जी त्रुटी राहते तिला स्थिर-स्थिती त्रुटी म्हणतात. समी. (९) मध्ये t → ∞ केले असता हिचे मूल्य Es मिळते.
यावरून असे दिसते की, (१) स्थिर-स्थिती त्रुटीचे Δ ML वर अवलंबून असते, (२) नियंत्रकाच्या लाभांकास अथवा श्यान क्रियेमुळे होणाऱ्या संदमक स्थिरांकात वाढ झाली असता त्रुटीचे मूल्य कमी होते आणि (३) सर्व परिस्थितीत स्थिर-स्थिती त्रुटीला अशून्य मूल्य असते.
प्रतिसादाची त्वरा ही कालस्थिरांकामुळे निश्चित होते. मोठ्या मूल्याचा संदमक स्थिरांक अथवा नियंत्रक अथवा लाभांक किंवा कमी मूल्याचे निरूढी परिबल यामुळे कालस्थिरांकाचे मूल्य कमी असते आणि त्या प्रमाणात प्रतिसादाची त्वराही जास्त असते.
प्रणालीचा प्रतिसाद या प्रश्नाचा जास्त खोलवर गणितीय अभ्यास केल्यास असे आढळून येते की, नियंत्रण प्रणालीच्या लाभांकामध्ये (किंवा स्थानांतरण फलनामध्ये) वाढ केली असता कालस्थिरांकाचे मूल्य कमी होते, हा एवढाच परिणाम होत नसून त्याच्या प्रतिसादाच्या स्वरूपात महत्त्वाचे बदल होतात. आ. ६ मधील वक्रांवरून ही गोष्ट कळून येईल. या आकृतीत (अ), (आ), (इ), (ई) यांकरिता क्रमवार लाभांक सारखा वाढत आहे, असे मानले आहे. आकृतीमध्ये पायरी फलन स्वरूपाचा बदल संकेत दिला असता त्यापासून मिळणाऱ्या त्रुटी संकेताचा प्रतिसाद दाखविला आहे. आ. ६ (अ) मध्ये लाभांक कमी व संदमन जास्त आहे. त्यामुळे येथे त्रुटी आपले स्थिर-स्थिती मूल्य (Es) घातांकीय रीतीने हळूहळू धारण करते. यामध्ये Es चे मूल्य सर्वांत अधिक आहे. (आ) मध्ये संदमन योग्य मूल्याचे असल्यामुळे प्रणालीत थोडीफार आंदोलने होत असली, तरी त्यांचे त्वरित संदमन होते. या प्रकारच्या चलनात त्रुटी तिच्या स्थिर-स्थिती मूल्यामधून अधिक लवकर जाते. (इ) आणि (ई) मध्ये आंदोलने इतक्या स्पष्ट स्वरूपात दिसतात की, त्यामुळे प्रणालीला स्थैर्य नाही असे म्हणावे लागते. सर्व दृष्टीने विचार करता प्रणालीत कार्य (आ) प्रमाणे होईल, असे अभिकल्पन करणे सोयीस्कर ठरते.
काही परिस्थितींत प्रणालीत आंदोलने का होतात यासंबंधी खालील स्पष्टीकरण देता येते. संवृत-वलय प्रणालीमध्ये एका स्थानी स्थानिक ऊर्जा उद्‌गमापासून मिळणारी ऊर्जा पुरविली जाते. (नियंत्रित राशीत झालेला बदल दुरुस्त करण्याकरिता लागणाऱ्या ऊर्जेपेक्षा ही स्थानिक ऊर्जा जास्त त्वरेने पुरविली गेली, तर पुन:प्रदाय क्रियेमुळे प्रणालीचे स्थैर्य भंग पावून ती अस्थिर बनते. तीमध्ये स्वनिर्मित आंदोलने येऊ लागतात. अशा परिस्थितीत स्थैर्यस्थापना हा जो नियंत्रणाचा मूळ हेतू तोच बाजूला राहतो. नियंत्रण प्रणालीचे योग्य असे अभिकल्पन करून त्यामध्ये या प्रकारचे अस्थैर्य निर्माण होणार नाही, अशी काळजी घेता येते. याचे विवरण पुढे केले आहे.
वरील विवेचनात प्रत्यक्ष प्रणालीचे गणितीय विश्लेषण न करता आदर्श वा अशा विश्लेषणाकरिता सुलभ अशी प्रणाली गृहीत धरण्यात आली आहे, हे लक्षात घेण्याजोगे आहे. या विश्लेषणात योग्य अशा ठिकाणी अनेक आसन्नीकरणे (अचूकतेच्या जवळपास असलेले अंदाज उपयोगात आणणे) करण्यात आली आहेत. प्रणालीच्या वर्तणुकीचे विशदीकरण करण्याकरिता त्यासाठी साध्या प्रतिकृती कल्पिल्या गेल्या आहेत. प्रत्येक अवकल समीकरण म्हणजे एक प्रतिकृती होते असे म्हणता येईल. उदा.,
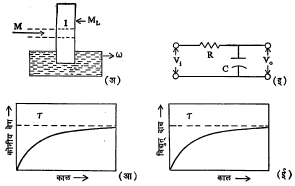
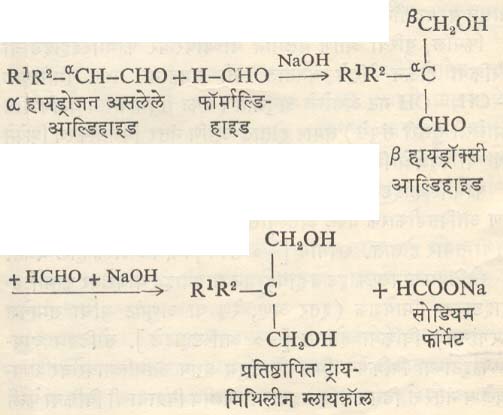
तुलनेकरिता नियंत्रण मंडळ त्याजवळ परत दाखविले आहे [आ. ७ (अ)]. नियंत्रण प्रणाली आणि तदनुरूप विद्युत् मंडल यांच्यापासून मिळणाऱ्या परिणामी राशी म्हणजे अनुक्रमे कोनीय वेग व विद्युत् दाब यांचे कालानुसार होणारे चलन एकसारखेच असते, हे आ. ७ (आ) व (इ) वरून दिसून येईल. अशी प्रतिकृती वापरल्यास दोन प्रकारचे फायदे होतात. विद्युत् मंडल विश्लेषणात वरील समीकरणाचे निरनिराळ्या विशिष्ट परिस्थितींत मिळणाऱ्या निर्वाहांसंबंधी जे विस्तृत संशोधन केले गेले आहे त्याचा सरळ व त्वरित उपयोग करून घेता येतो. दुसरा फायदा हा की, विद्युत् मंडलाच्या प्रतिसादाचे निरीक्षण व मापन करणे सुलभ असते. त्यामुळे एखाद्या नियंत्रण प्रणालीनुरूप विद्युत् मंडल तयार करून त्याचा प्रतिसाद पाहणे सोपे ठरते. याकरिता प्रतिकृतीचा वापर हा फायदेशीर ठरतो. या संदर्भात हे लक्षात ठेवले पाहिजे की, आदर्श प्रणाली व प्रत्यक्ष प्रणाली यांच्या कार्यात थोडाफार फरक राहणारच कारण प्रत्यक्ष प्रणालीत नियंत्रकाचे वस्तुमान, त्यामध्ये मिळणारा पिच्छट परिणाम (उदा., दंतचक्रांतील दात्यांसारख्या जवळ जवळच्या यंत्रभागांतील सैलसर जुळणीमुळे गतीमध्ये होणारा ऱ्हास) इ. गोष्टींचे परिणाम होतात. त्यामुळे आदर्श प्रणालीचे विश्लेषण करून त्यापासून काढलेल्या निष्कर्षांमध्ये थोडेफार फरक करणे आवश्यक ठरते.
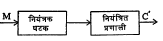
स्थिर-स्थिती कंप्रता प्रतिसाद : व्यवहारात त्रुटी संकेताचे कालपरिवर्ती चलन जटिल (गुंतागुंतीच्या) स्वरूपाचे असू शकते. त्यामुळे निर्माण होणारा नियंत्रक संकेत रेषीय प्रणालीत जटिल स्वरूपाचाच राहील हे उघड आहे. या दोन्ही संकेतांचे वर्णन गणितीय रीत्या जटिल फलनाचा उपयोग करूनच करता येणे शक्य होते. गणितशास्त्रामध्ये जटिल स्वरूपाच्या फलनाच्या परिणामाचे वर्णन त्यापेक्षा सुलभ अशा अनेक फलनांचा एकाच वेळी उपयोग करून करता येते, हे सुपरिचित आहेच. उदा., जे. बी. जे. फूर्ये यांनी दाखविल्याप्रमाणे कोणत्याही आकाराच्या कालपरिवर्ती फलनाचे वर्णन निरनिराळे परमप्रसर (स्थिर-स्थितीपासून होणारे कमाल स्थानांतरण) व कंप्रता (दर सेकंदाला होणाऱ्या कंपनांची संख्या) असलेल्या ज्या-वक्रीय फलनांच्या अध्यारोपणाने करता येत [⟶ फूर्ये श्रेढी तरंग गति]. या कारणाकरिता नियंत्रण प्रणालीचा प्रतिसाद काही ठराविक प्रमाणित आकाराच्या त्रुटी संकेताकरिता संशोधण्याचा किंवा मापन करण्याचा प्रघात आहे. या कार्याकरिता (१) एकक पायरी फलन आणि (२) ज्या-वक्रीय फलन स्वरूपाचे संकेत सर्वसाधारणपणे वापरले जातात. गणितीय विश्लेषणाच्या सुलभतेकरिता नियंत्रण प्रणालीचा प्रतिसाद (१) अस्थायी व (२) स्थिर-स्थिती ज्या-वक्रीय, या दोन भागांत वर्णन करण्यात येतो. अस्थायी प्रतिसादाचे वर्णन करण्याकरिता त्रुटी (किंवा कार्यकारी) संकेत पायरी फलनाच्या स्वरूपाचा आहे, असे गृहीत धरणे योग्य ठरते. या प्रकारच्या प्रतिसादाचे विवेचन आतापर्यंत झालेले आहे. या पुढील विभागात दुसऱ्या प्रकारच्या बदलाचे विवेचन केले आहे. या प्रकारच्या प्रतिसादावरून प्रणालीच्या स्थैर्याविषयी निष्कर्ष काढता येतात, हेही दाखविले आहे. रेषीय प्रणालीमध्ये जर त्रुटी संकेतात कालानुसार होणारा बदल ज्या-वक्रीय स्वरूपाचा असेल, तर त्यामुळे कार्यकारी संकेत M हाही त्याच स्वरूपाचा असेल व हा संकेत प्रणालीला दिला असता त्यापासून मिळणारे प्रदान C′ ही ज्या-वक्रीय असेल, हे उघड आहे. प्रतिसादाच्या विवेचनाकरिता M आणि C′ यांमधील परस्परसंबंधांचाच विचार केला तरी चालण्यासारखे आहे. रेषीय एकक धारणक्षमता प्रणालीकरिता या दोन राशींमधील संबंध खालील अवकल समीकरणाने दाखविला जातो.
जर B > > A तर समी. (१२) वरून असे दिसते की, परमप्रसर गुणोत्तराचे मूल्य लघू कंप्रतेकरिता जवळजवळ स्थिर असून कंप्रता एका ठराविक मर्यादेपेक्षा जास्त झाली, तर मात्र या राशीच्या मूल्यात त्वरेने घट होते. C′ आणि M यांच्यामधील कलांतर (एखाद्या स्थिर संदर्भापासून असणाऱ्या स्थितींमधील फरक) Ø चे मूल्यही कंप्रतेनुसार ०° ते – ९०° एवढा बदल दाखविते. C′ च्या कलेची मागसता (विलंब) बऱ्याच प्रमाणात नियंत्रण क्रियेच्या निरनिराळ्या टप्प्यांवर पडणाऱ्या कालविलंबाने घडून येते, हे उघड आहे. उरलेली मागसता नियंत्रण प्रणाली व नियंत्रित प्रणाली या दोहोंमधील घटकांच्या रचनेवर अवलंबून राहते. नियंत्रण प्रणालीत पुन:प्रदाय परिणाम ऋण प्रकारचा असला पाहिजे म्हणजे C′ या राशीतील बदलामुळे निर्माण होणारा कार्यकारी संकेत M तो बदल नाहीसा करील अशा स्वरूपाचा पाहिजे. या दोन राशींच्या कलांमध्ये जर फरक पडला, तर M चा एक घटकच (समकला असलेला) या कार्याकरिता उपयुक्त ठरेल. कलांमध्ये जेवढा फरक पडत जाईल, तेवढ्या प्रमाणात नियंत्रण प्रणालीची उपयुक्तता कमी होईल, हे स्पष्ट आहे. जर यदाकदाचित कलांमधील फरक आणखी वाढून १८०° एवढा झाला असे मानले, तर पुन:दाय क्रियेचे स्वरूप बदलून ती धन स्वरूपाची होईल. या परिस्थितीत C′ मध्ये झालेल्या बदलामध्ये दुरुस्ती न होता तिच्यात आणखी वाढ होईल व परिणामत: मध्ये आंदोलने निर्माण होतील, हे लक्षात येण्यासारखे आहे. यावरून प्रणालीचे स्थैर्य व स्थिर-स्थिती कंप्रता प्रतिसाद यांमध्ये निकट तऱ्हेचा संबंध आहे, हे उघड आहे.
प्रणालीचे स्थैर्य व नायक्विस्ट शर्त : नियंत्रण प्रणालीमधील मुख्य नियंत्रकाचे कार्य त्रुटी संकेताच्या प्रमाणात विशुद्धक कार्यकारी संकेत निर्माण करणे हे होय. त्वरित प्रतिसाद व कमी मूल्याची स्थिर-स्थिती त्रुटी मिळविण्याकरिता नियंत्रकाचा लाभांक उच्च असावा लागतो. पण त्यामुळे प्रणालीच्या स्थैर्यावर विपरीत परिणाम होतो. नियंत्रण प्रणालीकरिता एक विशिष्ट F (Ø) = ० अशा स्वरूपाचे समीकरण लागू पडते. याचे गणितीय दृष्ट्या विश्लेषण केल्यास संबंधित प्रणालीचे स्थैर्य या समीकरणाच्या बीजाच्या स्वरूपावर अवलंबून राहते, असे दाखविता येते. ही बीजे जर ऋण व सत् मूल्यी [⟶संख्या] असतील, तरच प्रणालीला स्थैर्य असते. हीच शर्त एच्. नायक्किस्ट यांनी विशेष उपयुक्त अशा स्वरूपात मांडली. या मांडणीकरिता ए. एल्. कोशी यांच्या एका प्रमेयाचा उपयोग गेला आहे.
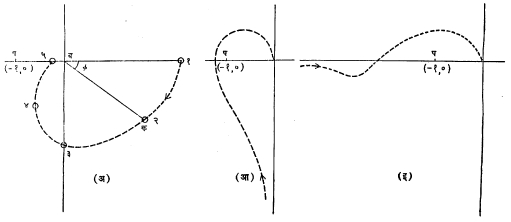
नायक्किस्ट आराखडा काढण्याकरिता नियंत्रण प्रणालीमधील पुन:प्रदाय विभाग काढून टाकतात आणि राहिलेल्या संचाकरिता निरनिराळ्या कंप्रतांकरिता मिळणारे परमप्रसर गुणोत्तर व कला या राशी प्रयोगाद्वारे मोजल्या जातात. या प्रदत्ताचा (माहितीचा) उपयोग करून ध्रुवीय आराखडा काढला जातो (आ. ९). यामध्ये कोणत्याही एका कंप्रतेकरिता मिळालेले परमप्रसर गुणोत्तर व कला हे एका सदिशाने (महत्ता व दिशा असलेल्या राशीने) दाखविले जाते. या सदिशाची लांबी परमप्रसर गुणोत्तराएवढी असते व त्याच्या दिशेवरून त्याची कला कळते. उदा., आ. ९ (अ) मध्ये बक ही लांबी परमप्रसर गुणोत्तर दर्शविते, तर Ø हा कोन त्याची कला दाखवितो. या सदिशाचे अंत्य बिंदू वाढत्या कंप्रता क्रमानुसार एका वक्राने जोडले जातात. कलेचे चिन्ह नेहमीच्या संकेत पद्धतीनुसार दाखविले जाते. सव्य (घड्याळाचे काटे फिरतात त्या) दिशेत मोजलेला कोन ऋण कला दाखवितो, तर त्याच्या विरुद्ध दिशेत मोजलेला कोन धन कला दाखवितो.
नायक्किस्ट शर्तीप्रमाणे कोणत्याही संवृत-वलय प्रणालीचे स्थैर्य तिच्यामधून पुन:प्रदाय विभाग काढून उरलेल्या अपूर्ण-वलय प्रणालीच्या कंप्रता प्रतिसादावरून निश्चित होते. अपूर्ण-वलय प्रणालीच्या नायक्किस्ट वक्रावरील क्ष-अक्षावर (– १, ०) हे सहनिर्देशक असलेल्या प या बिंदूच्या सगळ्यांत जवळचा बिंदू जर प च्या उजव्या बाजूस असेल, तर मूळ संवृत-वलय प्रणालीचे स्थैर्य असते. याउलट हा बिंदू प च्या डाव्या बाजूस असेल, तर ती प्रणाली अस्थिर असेल. आ. ९ (अ) मधील प्रणालीला या शर्तीप्रमाणे स्थैर्य आहे, तर (आ) व (इ) मधील प्रणाली अस्थिर आहेत, असे समजून येते.
नायक्किस्ट शर्तीचा उपयोग करून नियंत्रक प्रणालीचे स्थैर्य वाढविण्याकरिता व्यावहारिक उपाययोजना करता येते. या उपाययोजना दोन प्रकारच्या असतात : (१) उच्च ऊर्जा पातळी योजना,(२) नीच ऊर्जा पातळी योजना. पहिल्या प्रकारात श्यान-संदमित (ज्याचे उदाहरण विवेचनाकरिता वर घेतले होते) व आवर्त प्रवाह परिणामावर अवलंबून असणाऱ्या योजना यांचा समावेश होतो. या रीती मोठ्या प्रमाणात वापरल्या जातात पण यामध्ये कार्यशक्ती व जागा या दोन्हींचा अपव्यय होतो. दुसऱ्या प्रकारच्या पद्धतीत योग्य अशा प्रयुक्ती वापरून नियंत्रकाच्या प्रदान संकेतातच स्थैर्य आणणारे संकेत उपलब्ध होतील अशी व्यवस्था केलेली असते. हेच कार्य काही प्रणालींत विशिष्ट प्रतिपूरक मंडले वापरून केले जाते.
नैकरेषीय नियंत्रण प्रणाली : आतापर्यंतच्या विवेचनात रेषीय नियंत्रण प्रणालींचाच विचार करण्यात आला. खरे पाहिले असता व्यवहारात वापरल्या जाणाऱ्या सर्व नियंत्रण पद्धती बहुधा नैकरेषीय स्वरूपाच्याच असतात. त्यांचे कार्य काही परिस्थितीतच आसन्नपणे रेषीय आहे असे समजून त्यांचे वर्णन करणे शक्य होते. नैकरेषीय नियंत्रण प्रणालीकरिता अध्यारोपण तत्त्व यथार्थ ठरत नाही. कार्यकारी संकेत M व त्रुटी संकेत E यांमधील संबंध रेषीय नाही अशी प्रणाली नैकरेषीय स्वरूपाची असते. नैकरेषीय परिणाम दोन प्रकारे निर्माण होऊ शकतात. एखाद्या रेषीय प्रणालीमध्ये आकस्मित व मूलगामी स्वरूपाचे बदल झाले, तर (उदा., स्विचिंग मंडले) तिची क्रिया नैकरेषीय स्वरूपाची होते. एखाद्या प्रणालीमध्ये वापरलेल्या घटकाचे कार्य नैकरेषीय असल्यामुळे तिचे कार्यसुद्धा नैकरेषीय होते.
यांमध्ये नैकरेषीय चुंबकीय नियंत्रण प्रयुक्तींचा समावेश होतो. विद्युत् चुंबकीय प्रयुक्तीमध्ये चुंबकीकरण व ते घडवून आणणारा विद्युत् प्रवाह यांमधील संबंध नैकरेषीय असतो कारण काही मर्यादेपलीकडे विद्युत् प्रवाह वाढविला असता संपृक्ततेमुळे त्यापासून चुंबकीकरणात वाढ होत नाही. सर्वत्र आढळणारी दारावरील विद्युत् घंटा विद्युत् प्रवाहाने होणाऱ्या चुंबकीकरणावर अवलंबून असते पण या परिणामाचा उपयोग ‘चालू बंद’ या प्रकारची नियंत्रण प्रणाली बनविण्याकरिता होत असल्यामुळे यामधील नैकरेषीयत्व घटकाच्या नैकरेषीय वर्तणुकीमुळे निर्माण होत नाही, हे येथे नमूद केले पाहिजे. ‘चालू बंद’ प्रकारच्या सर्व नियंत्रण प्रणाली नैकरेषीय असतात असा उल्लेख मागे करण्यात आला आहेच.
नैकरेषीय प्रणालीचे सगळ्यांत प्रचलित उदाहरण म्हणजे ‘चालू बंद’ प्रणाली. या प्रणालीत फक्त तीनच अवस्था असतात. अवस्था (१) मध्ये नियंत्रण कार्य करीत नाही. अवस्था (२) मध्ये नियंत्रण एका दिशेत कार्य करते. उदा., स्विच चालू अवस्थेत असून प्रणालीतून विद्युत् प्रवाह वाहत असतो, अवस्था (३) मध्ये नियंत्रण दुसऱ्या प्रकारचे असते. उदा., स्विच बंद होऊन विद्युत् प्रवाह बंद असतो. या प्रणालीत नियंत्रण प्रत्यक्षात काही मर्यादित कालावधीमध्येच केले जाते, हे लक्षात ठेवण्याजोगे आहे. या प्रकारची नियंत्रण योजना साधे घटक वापरून तयार करता येते. यंत्रणा टिकण्याच्या दृष्टीने भक्कम असल्यामुळे बऱ्याच मोठ्या प्रमाणात हिचा वापर केला जातो. मोठ्या कार्यशक्तीचे नियंत्रण करण्याकरिता अशा प्रकारच्या प्रणाली विशेष उपयुक्त ठरतात. याचे सैद्धांतिक विश्लेषण करण्याकरिता एक नैकरेषीय प्रणाली दोन रेषीय प्रणालींशी आसन्नपणे समतुल्य आहे असे समजले जाते. याकरिता फक्त अवस्था (२) करिता एकरेषीय प्रणाली तर फक्त अवस्था (३) करिता दुसरी प्रणाली समतुल्य मानतात. या समतुल्य प्रणाली अर्थातच निरनिराळ्या निश्चित परिस्थितींत कार्य करतात. या प्रकारच्या कार्यपद्धतीकरिता सदृश उदाहरण इलेक्ट्रॉनिकीमध्ये सापडते. त्रिप्रस्थ नलिकेचे [⟶ इलेक्ट्रॉनीय प्रयुक्ति] कार्य प्रत्यक्षात नैकरेषीय असले, तरी कार्यकारी बिंदूच्या आसपास अभिलक्षण वक्र (नलिकेचे गुणधर्म दर्शविणारे वक्र) रेषीय समजून त्याकरिता एक समतुल्य रेषीय विद्युत् मंडल कल्पिता येते. नैकरेषीय प्रणालीचे विश्लेषण करण्याकरिता सर्वव्यापी गणितीय विश्लेषण पद्धत उपलब्ध नाही. काही विशिष्ट परिस्थितींकरिता यथार्थ रीतीचे संशोधन झालेले आहे. त्यांपैकी एका रीतीचा उल्लेख वर आलाच आहे. आलेखीय विश्लेषण ही रीत काही परिस्थितींत या कार्याकरिता वापरली जाते. नैकरेषीय नियंत्रण प्रणालींची वर्तणूक रेषीय प्रणालीच्यापेक्षा सर्वस्वी भिन्न असते. आदान नसताना सुद्धा स्थैर्यशील नैकरेषीय प्रणालीच्या प्रदानात स्थिर परमप्रसराची आदोलने असू शकतात. अशा प्रणालीचा मुक्त प्रतिसाद निरनिराळ्या प्राथमिक शर्तीकरिता मोठ्या प्रमाणात भिन्न असा असू शकतो. ही प्रणाली कालानुसार ज्या निरनिराळ्या अवस्था धारण करते त्यांमध्ये खंड अथवा भंग असू शकतात. सर्वांत शेवटी महत्त्वाचे म्हणजे जर आदान कालपरिवर्ती असेल, तर आदान नसलेल्या कंप्रताही अशा प्रणालीच्या प्रदानात आढळतात.
बहुविध धारणक्षमता प्रणाली : प्रस्तुत नोंदीतील बहुतेक विवेचन एकक धारणक्षमता प्रणालीकरिता विशदीकरणाच्या सुलभतेसाठी केले गेले आहे. प्रत्यक्षात बहुविध धारणक्षमता असलेल्या प्रणालीचा सुद्धा भरपूर उपयोग केला जातो. बहुविध धारणक्षमता प्रणालीत नियंत्रित राशींची संख्या एकापेक्षा जास्त असते. त्यामुळे त्याकरिता ऊर्जासंचयाचे प्रकारही अनेक असतात. ऊर्जासंचयांची जी संख्या असते तेवढ्याच राशी संख्येवर प्रणालीची ऊर्जा अवलंबून असते व तेवढ्याच कोटीचे अवकल समीकरण त्याकरिता वापरावे लागते. अशा प्रकारची समीकरणे सोडविण्यास कठीण असतात. या कार्याकरिता साधारणपणे खाली नमूद केलेल्या गणितीय रीती उपलब्ध आहेत.
(१) पारंपरिक पद्धत : हीमध्ये काही ठराविक स्वरूपाचा निर्वाह गृहीत धरून तो अवकल समीकरणात वापरला जातो. निर्वाहातील स्थिरांकांची मूल्ये दिलेल्या अटींचा उपयोग करून काढली जातात.
(२) लाप्लास रूपांतर पद्घत : हीमध्ये अवकल समीकरणाचे साध्या बैजिक समीकरणात रूपांतर केले जाते. बैजिक समीकरणातच प्राथमिक अटीचा अंतर्भाव करण्यात येतो. शेवटी व्यस्त रूपांतरण पद्धती वापरून इष्ट उत्तर अथवा निर्वाह मिळविला जातो [⟶ समाकल समीकरणे व रूपांतरे].
(३) अनुरूप संगणक : या प्रकारच्या संगणकामध्ये असणाऱ्या घटकामधील फेरफार अवकल समीकरणाच्या साहाय्याने दर्शविता येत असल्यामुळे याच्याद्वारे रेषीय व नैकरेषीय घटक असणाऱ्या नियंत्रक प्रणालीच्या प्रवृत्तीचे वर्णन करता येते. संगणकाच्या वापरामुळे निर्वाह मिळविण्याकरिता लागणारा वेळ अत्यल्प असतो [⟶ संगणक].
(४) अंकीय संगणक : ही प्रणाली अवकल समीकरणापेक्षा बैजिक समीकरणाचा निर्वाह काढण्याकरिता योग्य ठरते. यामुळे याचा उपयोग नियंत्रण प्रणालीच्या अस्थायी प्रतिसादाचा अभ्यास करण्याकरिता विशेषत: केला जातो [⟶ संगणक].
(५) बीज-बिंदुपथ तंत्र : या पद्धतीमध्ये पुन:प्रदाय नियंत्रण प्रणालीच्या विशेषक बैजिक समीकरणाच्या बीजाची मूल्ये काढली जातात. ही रीत अर्थातच कंटाळवाणी व जटिल आहे. संवृत-वलय प्रणालीच्या बीजांची मू्ल्ये तदनुरूप अपूर्ण-वलय प्रणालीच्या बीजांवरून काढण्याकरिता डब्ल्यू. आर्. एव्हान्झ यांनी एक सुलभ पद्धत शोधून काढली आहे. हिचा उपयोग विशेषपणे केला जातो.
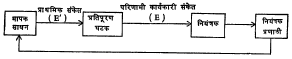
आधुनिक विकास : संवृत-वलय पुन:प्रदाय नियंत्रण प्रणालीमध्ये राशीत होणाऱ्या बदलाचे संपूर्णपणे प्रतिपूरण करणे शक्य होत नाही. ही मर्यादा नियंत्रण प्रणालीमुळेच बऱ्याच प्रमाणात उत्पन्न होते. या प्रणालीत नियंत्रित राशीचे प्रत्यक्ष मूल्य प्रमाणित मूल्याहून निराळे असल्यावाचून त्रुटी संकेत मिळत नाही आणि त्रुटी संकेत असल्याशिवाय नियंत्रकातून कार्यकारी संकेत मिळून राशीमध्ये झालेल्या बदलाचे प्रतिपूरण करण्याचा प्रयत्न होत नाही. कार्यकारी संकेताची निर्मिती व बदलाचे प्रतिपूरण या दोन्ही क्रिया मापक साधन व नियंत्रक यांच्या संवेदनक्षमतेवर अवलंबून राहतात. या सर्व कारणांमुळे ज्यामध्ये त्रुटी संकेत शून्य मूल्याचा आहे, अशी आदर्श परिस्थिती प्रणालीद्वारे निर्माण करणे शक्य होत नाही. याकरिता ‘प्रदाय अग्रगामी’ या संज्ञेची पर्यायी योजना संशोधिली गेली आहे. हिचे स्वरूप आ. १० मध्ये दाखविले आहे. या रीतीमध्ये नियंत्रित राशीचे मापन करून त्यापासूनच प्राथमिक कार्यकारी संकेत (E′) हा मिळाविला जातो. हा प्रतिपूरण घटकाच्या द्वारे नियंत्रकाकडे पाठविला जातो. प्रतिपूरण घटकाच्या द्वारे प्राथमिक संकेतात दुसरा संकेत अशा प्रमाणात मिसळला जातो की, त्यापासून नियंत्रकाकडे पाठविला जाणारा परिणामी कार्यकारी संकेत (E), राशीमध्ये जर काही प्रमाणित मूल्यापासून बदल झाला असेल, तर त्याचे पूर्णपणे प्रतिपूरण करतो. ही पद्धत यशस्वी करण्याकरिता प्रक्रिया गतिकीचे संपूर्ण ज्ञान असणे आवश्यक असते. याकरिता विक्षोभामुळे निर्माण झालेल्या राशीमधील बदलाचे प्रतिपूरण करण्याकरिता कोणत्या प्रकारचा संकेत लावणे आवश्यक आहे व हा विशुद्धक संकेत लावला असता नियंत्रण प्रणालीचा प्रतिसाद कसा मिळेल, याविषयीची अचूक माहिती आवश्यक असते. अशा प्रकारची माहिती नेहमीच उपलब्ध असते असे नाही. या व इतर काही तांत्रिक कारणांकरिता शुद्ध प्रदाय अग्रगामी योजना न वापरता संवृत-वलय पुन:प्रदाय व प्रदाय अग्रगामी यो दोन पद्धतींचा समन्वय करून मिळणारी योजना वापरण्याकडे कल आहे.
काही ठराविक चल राशींचे नियंत्रण न करता एखाद्या उत्पादन प्रक्रियेचे संकलित नियंत्रण करण्याकरिता स्वयंचलित नियंत्रण प्रणाली वापरात येऊ लागल्या आहेत. या प्रकारात अनेक राशींचे एकाच वेळी, अनेक नियंत्रण वलये वापरून, नियंत्रण केले जाते. प्रथमत: उत्पादक प्रक्रियेच्या संबंधित राशीचे नियंत्रण करून तिची मूल्ये ठराविक मर्यादेत ठेवणे हेच नियंत्रणाचे उद्दिष्ट असे पण सध्या या राशीची मूल्ये नियंत्रित करून प्रक्रियेचे इष्टतमीकरण करण्याकडे प्रवृत्ती आहे. प्रक्रियेपासून होणारे उत्पादन, तिची क्षमता, त्यापासून निर्माण होणाऱ्या उत्पादित वस्तूचे उत्पादन मूल्य इष्टतम होण्याकरिता त्यांची परस्पर मूल्ये काय असावीत हे ठरविले जाऊन नियंत्रण प्रणालीद्वारे या राशी ही मूल्ये धारण करतील असे पाहिले जाते. प्रक्रियेचे इष्टतमीकरण करण्याकरिता गणितीय विश्लेषण संगणकाच्या द्वारे करण्यात येते. नियंत्रण प्रणालीच्या उपयोगाचे स्वरूप अधिक सर्वव्यापी झाले आहे, हे या उदाहरणावरून लक्षात येते.
संदर्भ : 1. Barbe, E. C. Linear Control Systems, Sranton, 1963.
2. Elgerd O. I. Control Systems Theory, New York, 1967.
3. Gibson, J. E. Nonlinear Automatic Control, New York, 1963.
4. Holzbock W. G. Instruments for Measurement and Control, New York, 1962.
5. Savant C. J. Control Systems Design, New York, 1964.
6. Truxal, J. G., Ed. Control Engineers Handbook, New York, 1958.
7. Welbourne, D. B. Essentials of Control Theory for Mechanical Engineers, London, 1963.
चिपळोणकर, व. त्रिं.
“