ध्रुवणमिति

ध्रुवणमिति : (पोलॅरीमेट्री). जेव्हा प्रकाश किरणांची कंपने फक्त एकाच प्रतलात (पातळीत) होत असतात तेव्हा त्या प्रकाशाला रेखीय किंवा प्रतलीय ध्रुवित प्रकाश असे म्हणतात. असा रेखीय ध्रुवित प्रकाश काही विशिष्ट पदार्थातून जाऊ दिल्यास त्या प्रकाशाचे कंपन प्रतल विशिष्ट कोनांमधून फिरते असे आढळून येते. पदार्थांच्या या गुणधर्माला ध्रुवण घूर्णकता किंवा प्रकाशीय वलन असे म्हणतात व तत्संबंधीच्या अभ्यास शाखेला ध्रुवणमिती असे म्हणतात. कंपन प्रतल विशिष्ट प्रयोगात ज्या कोनामधून फिरते त्या कोनाला घूर्णन कोन किंवा वलन कोन (वा नुसतेच वलन) म्हणतात व हा कोन मापण्यासाठी वापरण्यात येणाऱ्या उपकरणाला ‘ध्रुवणमापक’ असे म्हणतात. ‘ध्रुवण घूर्णक’ पदार्थातून पलीकडील प्रकाश उद्‌गमाकडे पाहणाऱ्या निरीक्षकाच्या दृष्टीने कंपन प्रतल घड्याळाच्या काट्यांच्या दिशेने फिरवल्यास त्या पदार्थाला दक्षिणावर्ती (किंवा दक्षिणवलनी) व त्याच्या उलट दिशेने फिरल्यास त्याला वामावर्ती (किंवा वामवलनी) असे म्हणतात. दक्षिणावर्ती घूर्णन (+) या चिन्हाने व वामावर्ती घूर्णन (-) या चिन्हाने दर्शविले जाते.

सूर्यप्रकाश किंवा कोणत्याही प्रकाश-उद्‌गमापासून मिळणारा प्रकाश निकोल लोलकातून [→ प्रकाश] जाऊ दिल्यास बाहेर येणारा प्रकाश प्रतलीय ध्रुवित असतो. म्हणजेच या निकोलाच्या साहाय्याने साध्या प्रकाशापासून प्रतलीय ध्रुवित प्रकाश मिळतो. म्हणून त्याचा उपयोग ‘ध्रुवक’ (किंवा ध्रुवणकारक) या नात्याने केला आहे, असे म्हणतात. ध्रुवकापुढे दुसरा निकोल त्याला समांतर स्थितीत ठेवल्यास त्या दोहोंमधून प्रकाश बाहेर येतो परंतु प्रकाशाची दिशा हा अक्ष कल्पून त्याभोवती दुसरा निकोल हळूहळू फिरवत गेल्यास बाहेर येणाऱ्या प्रकाशाची तीव्रता कमी होत जाते व दुसरा निकोल ९० अंशांमधून फिरविला गेल्यानंतर दोघांमधून बाहेर येणाऱ्या प्रकाशाची तीव्रता शू्न्य होते. म्हणजेच काहीही प्रकाश बाहेर येत नाही. या वेळी त्या दोन निकोलांचे प्रकाशीय अक्ष परस्परांशी काटकोन करतात आणि मग ते निकोल जात्य स्थितीत आहेत, असे म्हणतात. या रचनेतील दुसऱ्या निकोलाला विश्लेषक असे म्हणतात. ध्रुवणमापकात ही जात्य स्थिती अत्यंत महत्त्वाची आहे. ध्रुवण घूर्णनाचाआविष्कार दाखविणाऱ्या पदार्थांना ध्रुवण घूर्णक (किंवा प्रकाशीय दृष्ट्या क्रियाशील) व न दाखविणाऱ्या पदार्थांना ध्रुवण अघूर्णक असे म्हणतात.

ध्रुवण घूर्णकतेचे नियम : प्रत्यक्ष प्रयोगावरून जे. बी. बायो (१७७४—१८६२) या फ्रेंच भौतिकीविज्ञांनी ध्रुवण घूर्णकतेबद्दल पुढील नियम बसविले : (१) ध्रुवण कोन ध्रुवण घूर्णक पदार्थावर अवलंबून असतो. (२) त्याचप्रमाणे तो ध्रुवण घूर्णकाचे तापमान व (३) वापरलेल्या प्रकाशाच्या तरंगलांबीवरही अवलंबून असतो. (४) ध्रुवण घूर्णक पदार्थांतील प्रकाशमार्गाचा लांबीच्या सम प्रमाणात ध्रुवण कोन असतो. (५) ध्रुवण घूर्णक पदार्थाचे ध्रुवण अघूर्णक द्रवात विद्राव किंवा मिश्रण केल्यास त्या मिश्रणामुळे मिळणारा ध्रुवण कोन, मिश्रणातील किंवा विद्रावातील ध्रुवण घूर्णकाच्या सांद्रतेच्या (एकक घनफळातील वस्तुमानाच्या) सम प्रमाणात असतो.

ध्रुवणमितीचे उपयोग : ज्या पदार्थांचे रेणू वा स्फटिक असममित (एखाद्या बिंदूच्या वा प्रतलाच्या सापेक्ष एकसारखी मांडणी नसलेले) असतात. त्यांनाच ध्रुवण घूर्णकतेचा गुण असतो, असे प्रयोगावरून दिसून येते. केवळ स्फटिकाच्या असममितीमुळे आलेली ध्रुवण घूर्णकता पदार्थ स्फटिकरूप आहे तोपर्यंतच टिकते. पदार्थ वितळल्यास वा एखाद्या द्रवात विरघळून त्याचा विद्राव बनविल्यास स्फटिकरूप नाहीसे होते. म्हणून अशा पदार्थांची ध्रुवण घूर्णकताही नष्ट होते. असममित रेणू असलेला पदार्थ एखाद्या विद्रावात अंतर्भूत असल्यास त्याची त्या विद्रावातील वरील पाचव्या नियमाच्या आधारे सांद्रता निश्चित करता येते. व्यवहारात आढळणारा अशा प्रकारचा एक पदार्थ म्हणजे साखर होय. विद्रवातील साखरेचे प्रमाण निश्चित करण्यासाठी ध्रुवणमापकाचा उपयोग इतका रूढ आहे की, त्यामुळे या कामासाठी वापरला जाणारा ध्रुवणामापक हा शर्करामापक याच संज्ञेने ओळखला जातो. याशिवाय कित्येक अल्कलॉइडे, स्टेरॉइडे व औषधी कार्बनी संयुगे याचे मापनही ध्रुवणमापकाच्या साहाय्याने करता येते.

विशिष्ट घूर्णन : (विशिष्ट वलन). ध्रुवण घूर्णक पदार्थाची घूर्णनक्षमता ही विशिष्ट घूर्णन (α) या राशीने व्यक्त करतात. प्रकाशाच्या कोणत्या तरंगलांबीसाठी व कोणत्या तापमानाला हे α चे मूल्य दिले आहे, ते पादांक व शिरांक वापरून दाखवितात. सामान्यतः ही मूल्ये २०^° से. या तापमानाला व सोडीयमाच्या D या (पिवळ्या रंगाच्या) वर्णरेषेसाठी म्हणजे ५,८९० Å (Å = अँगस्ट्रॉम = १०^-८ सेमी.) तरंगलांबीसाठी दिली जातात, मग ती [α]_D²⁰ असे लिहून व्यक्त केली जातात. एखाद्या विशिष्ट विद्रवातून प्रकाशाचा मार्ग/सेंमी. लांबीचा असून त्या विद्रावात घूर्णकाचे प्रमाण c ग्रॅ. प्रती घ. सेंमी. असेल व त्यायोगे प्रकाशाचे कंपन प्रतल θ^° या कोनातून फिरत असेल, तर [α] पुढील सूत्रावरून काढता येते.

 विविध पदार्थांच्या विशिष्ट घूर्णनाची मूल्ये काळजीपूर्वक निश्चित केलेली असून त्यांची कोष्टके उपलब्ध आहेत. α माहीत असल्यास प्रयोगावरून l व θ मोजून त्यावरून c चे मूल्य काढता येते. म्हणजे यासाठी या घूर्णन कोनाचे अचून मापन करणे आवश्यक आहे. ध्रुवणमापक : घूर्णन कोनाचे मापन करण्यासाठी ध्रुवणमापक हे साधन वापरतात. ध्रुवणमापकांचे अनेक प्रकार असून त्यांपैकी तीन प्रातिनिधिक उपकरणांची माहिती येथे दिली आहे.

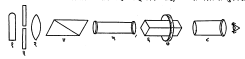
साधा ध्रुवणमापक : यात एक ध्रुवक निकोल व दुसरा विश्लेषक निकोल एका सरळ रेषेत ठेवलेले असून त्यांच्या दरम्यान परीक्ष्य विद्राव भरलेली नळी ठेवलेली असते. (आ. १) विश्लेषकाभोवती अंशांकित वर्तुळाकार मोजपट्टी असून तिच्या साहाय्याने विश्लेषक किती अंशांच्या कोनामधून फिरविला ते मोजता येते.

(१) या सोडियम दिव्यापासून मिळणाऱ्या एकवर्णी (पिवळ्या) प्रकाशाचे (२) या बहिर्गोल भिंगाने थोडेसे केंद्रीकरण करून ध्रुवकावर पाडतात. (५) ही नळी प्रथम शुद्ध पाण्याने भरून मध्यंतरी ठेवतात व (८) या नेत्रिकेतून पाहून विश्लेषक (६) असा फिरवतात की, पलीकडून येणारा प्रकाश पूर्णपणे नाहीसा व्हावा. या परिस्थितीत (७) या मोजपट्टीवरील θ₁ या कोनाची नोंद करतात. मग परीक्ष्य नळी इष्ट विद्रावाने भरून पुन्हा त्याच जागी ठेवल्यावर प्रकाशाच्या कंपन प्रतलाच्या घूर्णनामुळे नेत्रिकेतून प्रकाश दिसू लागतो. तो प्रकाश पुन्हा नाहीसा करण्यासाठी योग्य दिशेने विश्लेषक आणखी फिरवितात आणि प्रकाश दिसेनासा झाल्यावर θ₂ या कोनाची नोंद करतात. यावरून θ₂ (= θ₂ – θ₁) काढता येतो.

या प्रकारच्या ध्रुवणमापकाच्या साहाय्याने फारशी अचूक मापने करता येत नाहीत. एकतर संपूर्ण अंधार केव्हा झाला हे ओळखण्याची डोळ्यांची क्षमता फार कमी असते. दुसरे म्हणजे आजूबाजूला प्रकाश डोळ्यावर आल्यामुळे ही क्षमता आणखी कमी होते. यासाठी मापन अंधाऱ्या खोलीत करतात परंतु बराच वेळ काम केल्यानंतर डोळ्यांना आलेल्या थकव्यामुळे पुन्हा डोळ्यांची क्षमता कमी होते.

प्रत्यक्ष प्रयोगावरून असे दिसून आले आहे की, संपूर्ण अंधार केव्हा झाला हे ओळखणे अवघड असते परंतु शेजारची दोन क्षेत्रे दोन प्रकाश शलाकांनी प्रकाशित केल्यास त्या क्षेत्रांच्या दीप्तीची (तेजस्वीपणाची) तुलना डोळा फार चांगल्या तऱ्हेने करू शकतो. या दोन क्षेत्रांची दीप्ती समान केव्हा होते, ते खूपच अचूकपणे ओळखता येते. आधुनिक ध्रुवणमापकात या गोष्टींचा उपयोग केलेला असतो. अशा प्रकारच्या ध्रुवणमापकाला अर्धछाया ध्रुवणमापक म्हणतात.

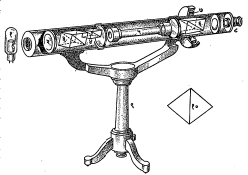
लिपिख अर्धछाया ध्रुवणमापक : अर्धछाया तत्त्वावर आधारलेल्या ध्रुवणमापकात लिपिख यांनी तयार केलेला ध्रुवणमापक सर्वांत जास्त अचूक व संवेदनशील आहे. याच्या आ. २ मध्ये दाखविलेल्या रचनेवरून हे लक्षात येईल की, याची रचना सामान्यपणे साध्या ध्रुवणमापकासारखीच आहे. फक्त (४) हा अर्धछायाकारक निकोल ध्रुवक आणि परीक्ष्य नळी यांच्या मध्ये घातला आहे. ही मुख्य सुधारणा आहे.

कोणत्याही निकोलामधून बाहेर पडणाऱ्या प्रकाशाचे कंपन प्रतल त्या निकोलाच्या पुढील बाजूच्या पृष्टाच्या आखूड कर्णाला समांतर असते. या प्रतलाला आपण त्या निकोलाचे कंपन प्रतल म्हणू. लिपिख अर्धछायाकारक निकोल ध्रुवकाच्या पुढे व त्याचा वरचा अर्धा भाग झाकेल असा बसविलेला असतो. त्याचप्रमाणे त्या दोघांच्या कंपन प्रतलामध्ये एक लहानसा कोन होईल अशी योजना केलेली असते. ध्रुवकामधून बाहेर येणाऱ्या प्रकाश शलाकेचा फक्त वरचा अर्ध लिपिख निकोलामधून जातो. त्यामुळे परीक्ष्य नळीवर पडणाऱ्या प्रकाश शलाकेचे दोन भाग होतात. वरच्या व खालच्या अर्धावर पडणाऱ्या प्रकाशाची कंपन प्रतले परस्परांशी पूर्वनियोजित कोन करतात त्याला अर्धछाया कोन असे म्हणतात. विश्लेषक हा ध्रुवकाशी जात्य स्थितीत ठेवला, तर खालचे अर्धे दृष्टिक्षेत्र पूर्णपणे काळे आणि वरचे अर्धे चांगले प्रकाशित दिसते. (आ. ३ अ). उलट विश्लेषक हा लिपिख निकोलाला जात्य केल्यास वरचे अर्धे क्षेत्र काळे आणि खालचे अर्धे चांगले प्रकाशित दिसते. (आ. ३ आ). या दोहोंच्या दरम्यान विश्लेषकाची अशी एक स्थिती मिळते की, तेव्हा दृष्टीक्षेत्राचे दोन्ही अर्ध सारखेच अंधारित दिसतील (आ. ३ इ.) याच स्थितीत मोजपट्टीवरील मागे सांगितलेल्या θ₁ व θ₂ च्या कोनांची नोंद करावयाची असते. साध्या ध्रुवणमापकापेक्षा या पद्धतीच्या ध्रुवणमापकाच्या साहाय्याने घूर्णन कोनाचे मापन खूपच जास्त अचूक  (१/१०० अंशापर्यंत) करता येते.

परंतु यातही वरील स्थिती आली की नाही ते निश्चित करण्यासाठी मानवी नेत्राऐवजी प्रकाशविद्युत् वर्धक[ → प्रकाशविद्युत्] या प्रभावी साधनाचा उपयोग केल्यास मापनाची अचूकता १० पट वाढू शकते. इतकेच नाही, तर वरील रचनेत योग्य ते फेरफार करून विश्लेषक फिरविणे व कोनांची नोंद घेणे या क्रिया स्वयंचलित करता येतात. रेणू मधील अणूंची स्थाने निश्चित करण्यासाठी ध्रुवणमापनाचा फारच चांगला उपयोग होतो. त्यासाठी अशी स्वंयचलीत उपकरणे वापरणे जरूर असते. प्रकाशविद्युतीय ध्रुवणमापकाचे वेगवेगळे नमुने उपलब्ध आहेत. त्यांपैकी एकाची रचना व कार्यपद्धती खाली दिली आहे.

बेट्स प्रकाशविद्युतीय ध्रुवणमापक : त्रिमितीय रसायनशास्त्रात विशिष्ट पदार्थाचे वेगवेगळ्या तरंगलांबीच्या प्रकाशाचे घूर्णन मोजून त्यावरून घूर्णन व तरंगलांबी यांचे आलेख काढावे लागतात, या आलेखांना प्रकाश घूर्णनीय अपस्करण (ORD) आलेख म्हणतात. त्यांच्यावरून रेणूंच्या रचनेबद्दल निश्चित अंदाज करता येतात. हे ORD आलेख मिळविण्यासाठी बेट्स यांच्या प्रकाशविद्युतीय ध्रुवणमापकाचा उपयोग करतात. त्याची रचना व कार्यपद्धती पुढीलप्रमाणे आहे : (१) या झेनॉन (वा झिर्कोनियम) प्रज्योत दीपापासून मिळणारा अखंड वर्णपटीय प्रकाश (३) या एकवर्णकावर पडतो व त्यामधून इष्ट त्या तरंगलांबीचा प्रकाश बाहेर घेता येतो. तो (४) या पोलरॉइडावर पडून प्रतलीय ध्रुवित होतो ( येथे पोलरॉइड निकोलाप्रमाणेच कार्य करतो). हा प्रतलीय ध्रुवित प्रकाश (५) या सु. १० सेंमी लांबीच्या काचेच्या दंडामधून जातो. दंडाभोवतालच्या वेटोळ्यातून प्रत्यावर्ती (उलटसुलट दिशांना वाहणारा) विद्युत् प्रवाह सोडलेला असतो. याचा परीणाम असा होतो की, त्यातून बाहेर येणाऱ्या प्रकाशाचे कंपन प्रतल आपल्या मूळ दिशेच्या दोन्ही बाजूंना (सु. ३ अंशामधून) डोलू लागते.

हा प्रकाश मग (६) या कोशात ठेवलेल्या परीक्ष्य पदार्थातून जातो आणि त्याच्या कंपन प्रतलाचे धूर्णन होते. त्याशिवाय त्याच्या कंपन प्रतलाचे दोलनही चालू असतेच. अशा तऱ्हेने त्या दोलनाची माध्य (सरासरी) स्थिती इष्ट पदार्थाच्या घूर्णन कोनाएवढ्या कोनातून एका बाजूला ढळते. (७) हा काच-दंड (५) सारखाच परंतु त्याच्या निम्म्या लांबीचा असून त्याच्या भोवतालच्या वेटोळ्यात एकदिश विद्युत् प्रवाह सोडलेला असतो. या प्रवाहाची दिशा व मूल्य जरूर त्याप्रमाणे बदलता येते. या रचनेतून जाणाऱ्या प्रकाशाचे ध्रुवण घूर्णन होते व हा घूर्णन कोन वेटोळ्यातून जाणाऱ्या विद्युत् प्रवाहाच्या मूल्याशी सम प्रमाणात असतो. (७) मधून बाहेर पडलेला प्रकाश मग (८) या विश्लेषक पोलरॉइडामधून जाऊन शेवटी (९) या प्रकाशविद्युत् गुणक साधनावर पडतो व त्यामुळे त्याच्यात विद्युत् प्रवाह निर्माण होतो.(७) भोवतालच्या वेटोळ्यातील विद्युत् प्रवाह असा जुळवितात की, त्यामुळे (६) मधील इष्ट पदार्थामुळे झालेल्या ध्रुवण घूर्णनाचे बरोबर निराकरण व्हावे. प्रकाशाच्या कंपन प्रतलाच्या दोलनामुळे (९) वर पडणाऱ्या प्रकाशाची तीव्रता एकसारखी पुनरावृत्तीने बदलत असते. त्यानुसार गुणकातून मिळणारा विद्युत् प्रवाह कमी जास्त होत असतो. बरोबर निराकरण स्थिती येते तेव्हा विद्युत् प्रवाहाची लागोपाठची दोन महत्तम मूल्ये परस्परांना समान होतात. या वेळी (७) च्या वेटोळ्यातील विद्युत् प्रवाह मूल्यावरून मूळ पदार्थाचा घूर्णन कोन काढता येतो.

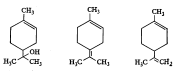
संरचना ठरविण्यासाठी ध्रुवण घूर्णकतेचा उपयोग : एखाद्या संयुगावर रासायनिक विक्रिया घडविल्याने निर्माण होणाऱ्या संयुगाला जर दोन पर्यायी संरचना असतील, तर त्यांपैकी कोणती त्या संयुगाला द्यावी, हे काही पुरावा मिळवून ठरवावे लागते. त्या दोन संरचनापैकी एकच जर ध्रुवण घूर्णनक्षम असेल, तर मिळालेल्या संयुगाला घूर्णन आहे किंवा नाही, हे पाहून त्याची संरचना निश्चित करणे सोपे असते. उदा., लिमोनिनाची संरचना आल्फा टर्पिनिऑल (सूत्र १) या संयुगाचे निर्जलीकरण (रेणूतून पाण्याचा रेणू काढून टाकणे) केले म्हणजे लिमोनीन हे संयुग बनते. त्यासाठी दोन पर्यायी संरचना (सूत्र २ आणि ३) शक्य आहेत. त्यांपैकी एकच घूर्णनक्षम आहे (सूत्र ३) लिमोनीन घूर्णनक्षम आहे तेव्हा त्याची संरचना सूत्र २ प्रमाणे नसून सूत्र ३ प्रमाणे असली पाहिजे, हे निर्विवाद सिद्ध होते कारण या संरचनेतच एक असममित कार्बन अणू आहे.

ध्रुवण घूर्णकता व विन्यास : संयुगाच्या विन्यास [ त्रिमितीय अवकाशातील मांडणी → त्रिमितीय रसायनशास्त्र] ठरविण्यासाठीही ध्रुवण घूर्णकता कित्येकदा उपयोगी पडते. उदा., D— एरिथ्रोज हे संयुग घूर्णनक्षम आहे. त्यामधील असममित कार्बन अणूंचे विन्यास पुढीलप्रमाणे ठरविता येतात. या संयुगाचे ⇨ क्षपण  केल्यास ४ हायड्रॉक्सी गट असलेले अल्कोहॉल बनते व ते घूर्णनक्षम नाही. यावरून अल्कोहॉलातील असममित कार्बन अणूंचे विन्यास सूत्र ५ मध्ये दाखविल्याप्रमाणे असले पाहिजेत, हे उघड आहे. ज्याअर्थी हे अल्कोहॉल D— एरिथ्रोजापासून, CHO गटाचे CH₂OH मध्ये रूपांतर होऊन झाले आहे त्याअर्थी मधल्या दोन कार्बन अणूंचे विन्यास जसे मूळ संयुगात होते तसेच असणार. यावरून D— एरिथ्रोज याचा विन्यास सूत्र ४ प्रमाणे असला पाहिजे, असा निष्कर्ष निघतो.

रेणवीय घूर्णन : संयुगाच्या विशिष्ट घूर्णनाला [α] त्याच्या रेणुभाराने (M) गुणले आणि १०० ने भागले म्हणजे रेणवीय घूर्णन मूल्य [M] मिळते.

रेणवीय घूर्णन आणि विन्यास यांचा परस्परसंबंध आहे. त्यासंबंधीचे मुख्य नियम पुढे दिल्याप्रमाणे आहेत.

सारखी असममिती [ → त्रिमितीय रसायनशास्त्र]  असलेल्या अ आणि आ या संयुगांवर एकच रासायनिक विक्रिया करून अ^′ व आ^′ हे अनुजात बनविले व त्यांची रेणवीय घूर्णने [M] मोजली, तर असे दिसून येते की, अनुजातांच्या रेणवीय घूर्णन मूल्यातून त्या त्या मूळ संयुगांची रेणवीय घूर्णन मूल्ये वजा केली, [M]_अ′ – [M]_अ आणि [M]_आ′ – [M]_आ तर येणाऱ्या संख्याची चिन्हे सारखी (म्हणजे दोन्ही + अथवा दोन्ही – ) येतात.

यासारखाच आणखीही एक नियम आहे. त्याचा उपयोग स्टेरॉइडे व टर्पिनॉइडे या वर्गांतील कित्येक संयुगांच्या संरचना आणि विन्यास ठरविण्यासाठी प्रथमतः झाला. स्टेरॉइडांच्या मूळ सांगाड्यात जर वेगवेगळे गट प्रतिष्ठापित करून मिळणाऱ्या संयुगांची रेणवीय घूर्णन मूल्ये काढली व त्यांवरून मूळ सांगाड्याच्या रेणवीय घूर्णनात किती भर पडते किंवा किती घट होते ते ठरविले, तर असे आढळते की, भर किंवा घट ही ते ते गट, त्यांची रेणूतील स्थाने आणि विन्यास यांनुसार वेगवेगळी असते.

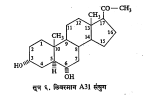
ज्यांच्या संरचना आणि विन्यास निश्चित झालेले होते अशा संयुगांच्या रेणवीय घूर्णनावरून मूळ सांगाड्यांचे रेणवीय घूर्णन मूल्य आणि वेगवेगळ्या गटांच्या प्रतिष्ठापनाने त्यास पडणारे फरक यांचे आकडे उपलब्ध झाले आहेत, त्यांचा उपयोग करून संरचना आणि विन्यास यांसंबधी महत्त्वाचे निष्कर्ष काढता येतात. उदा., सूत्र ६ मध्ये दाखविलेल्या संयुगातील ६ या ठिकाणच्या OH गटाची विन्यास निश्चिती. या संयुगाचा सांगाडा स्टेरॉइडी असून त्यातील ३ या ठिकाणचा OH गट आल्फा प्रकारचा (रेणूप्रतलाच्या खाली जाणारा) आहे व त्यामध्ये १७ या ठिकाणी CO·CH₃ गट आहे, हे ज्ञात होय पण ६ या ठिकाणी असलेला OH गट रेणुप्रतलाच्या खाली जाणारा (आल्फा प्रकारचा) की वर येणारा (बीटा प्रकारचा) आहे, हे माहीत नव्हेत. हा प्रश्न सोडविण्यासाठी संयुगाचे रेणवीय घूर्णन काढले. ते + ३५१ भरले. ६ या ठिकाणी H अणू असलेल्या संयुगाचे रेणवीय घूर्णन + ३०९ असते हे ज्ञात होते. यावरून ६ या ठिकाणच्या H अणूचे OH गटाने प्रतिष्ठापन झाल्यामुळे रेणवीय घूर्णनात किती फरक पडला, हे काढता येते. तो ३५१—३०९ असते हे ज्ञात होते. यावरून ६ या ठिकाणच्या H अणूचे OH गटाने प्रतिष्ठापन झाल्यामुळे रेणवीय घूर्णनात किती फरक पडला, हे काढाता येते. तो ३५१ – ३०९ = ४२ येतो. असा OH गट आल्फा प्रकारचा असेल तर ५५ किंवा त्याच्या जवळपास फरक पडतो व बीटा प्रकारचा असेल, तर –५० इतका पडतो, हे कोष्टकावरून माहीत होते. यावरून सदर संयुगामधील ६ या ठिकणचा OH गट आल्फा प्रकारचाच असला, पाहिजे असा निष्कर्ष निघाला व त्याचा विन्यास सिद्ध झाला.

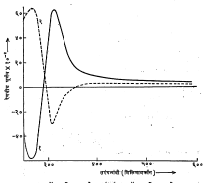
कॉटन परिणाम आलेख : वेगवेगळ्या तरंगलांबीचा प्रकाश वापरून काढलेली विशिष्ट घूर्णन मूल्ये य अक्षावर व प्रकाश तरंगलांबी क्ष अक्षावर घेऊन काढलेल्या आलेखाला प्रकाश घूर्णनीय अपस्करण आलेख (ORD) म्हणतात. अशा आलेखात विविधता आढळते. काही संयुगांची विशिष्ट घूर्णन मूल्ये वाढत जाणाऱ्या तरंगलांबीबरोबर प्रथम कमीकमी होत जाऊन विशिष्ट मर्यादेनंतर एकदम वाढू लागतात व त्यानंतर वरीलप्रमाणे पुन्हा घटत जातात किंवा याच्या उलट प्रथम वाढत जाऊन नंतर घटत जातात. त्यामुळे त्यांच्या आलेखात शिखरे व दऱ्या आढळतात. याला कॉटन परिणाम असे त्याच्या संशोधकाच्या नावावरून म्हणतात. आ. ५ मध्ये असे काही आलेख दाखविले आहेत ज्या आलेखात दरी कमी तरंगलांबीस आणि शिखर जास्त तरंगलांबीस येते, त्याला घन कॉटन परिणाम आलेख व याच्या विरुद्ध प्रकारच्या आलेखाला ऋण कॉटन परिणाम आलेख म्हणतात.

एखाद्या संयुगात कार्बोनिल गट (CO) असममित परिसरात असेल, तर कॉटन परिणाम आलेख मिळतो, असे आलेख वैशिष्ट्यपूर्ण असतात. संयुगाच्या रेणूत असणाऱ्या कार्बोनिल गटाच्या स्थानानुसार त्यांमध्ये ठळक फरक आढळतात. शिवाय या गटापासून दूरवर जरी काही रासायनिक फेरफार असला, तरी त्याचा परिणाम आलेखावर होत नाही. या वस्तुस्थितीचा उपयोग करून कित्येक स्टेरॉइडी संयुगांच्या संरचना व विन्यास निश्चित करता आले.

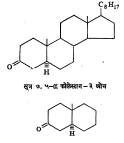
कार्बोनिल गट रेणूच्या अग्रभागी असेल, तर त्या स्टेरॉइडी संयुगाचा आलेख व तशा तऱ्हेच्या विन्यास असलेल्या दुसऱ्या एखाद्या वर्गाच्या संयुगाचा आलेख एकाच तऱ्हेचे असतात. उदा ५–α कोलेस्टान – ३ ओन (सूत्र ७) व ट्रान्स डेकॅलोन (सूत्र ८)  ही दोन्ही संयुगे घन कॉटन परिणाम आलेख देतात. कॉटन परिणामाचा उपयोग करून अष्टक नियमाच्या योगाने ५, ६ व ७ कार्बन वलयी कीटोनांचे विन्यास निश्चित करता येतात. या पद्धतीचा तपशील बराच गुंतागुंतीचा असल्यामुळे येथे दिलेला नाही.

संदर्भ :  1. Schwarz, J. C. P., Ed. Physical Methods in Organic Chemistry, Edinburgh and London, 1964. 

            2. Smith  C. J. A Degree Physics, Part III, Optics, London, 1960. 

            3. Valasek, J. Introduction to Theoretical and Experimental Optics, New York, 1949. 

            4. Willard, H. H. Merritt, L. L. Dean J. A. Instrumental Methods of Analysis, New York, 1958.

परांजपे, य. रा. पानसरे, व. स. केळकर, गो. रा. पुरोहित, वा. ल.

“