द्रायुयामिकी

द्रायुयामिकी : कोणत्याही प्रवाही पदार्थास द्रायू ही संज्ञा आहे. द्रव व वायू अशा द्रायूच्या दोन भिन्न प्रकारच्या अवस्था होत. सामान्यपणे द्रव जवळजवळ असंकोच्य असतात म्हणजेच बाहेरील दाबाचा त्यांच्या घनफळावर फारच थोडा परिणाम होतो. याउलट वायू संकोच्य असून बंदिस्त असल्यासच संतुलित अवस्थेत राहू शकतात. द्रव पदार्थाला मुक्तपृष्ठ असू शकते, तर वायूला तसे असत नाही. वायूवर सर्व बाजूंनी बंदिस्त असे आवरण नसेल, तर त्याचे अमर्याद प्रसरण होऊ शकते. द्रव आणि वायू यांचे भौतिक आणि औष्णिक गुणधर्म भिन्न प्रकारचे आहेत.

एखाद्या पदार्थाच्या दोन लगतच्या थरांमधील सापेक्ष गतीला जो आंतरिक विरोध असतो, त्य़ाला त्या पदार्थाची श्यानता म्हणतात. घन पदार्थामध्ये हा विरोध खूपच असतो. द्रव पदार्थात अत्यल्प असतो, तर वायूमध्ये जवळजवळ नसतोच. परस्परांना समांतर पण विरुद्ध दिशायुक्त अशा दोन अल्प मानाच्या प्रेरणा (कर्तरी प्रेरणा) लागू केल्यास ज्या दोन थरांवर या प्रेरणा लागू असतील त्यांना सापेक्ष गती प्राप्त होते. हे द्रायूच्या बाबतीत सहज शक्य असते किंबहुना या गुणधर्मामुळेच द्रायूंना प्रवाहीपणा प्राप्त झाला आहे. नेहमीच्या वापरातील मध व पाणी या दोन द्रवांमध्ये मधाची श्यानता पाण्यापेक्षा जास्त आहे. यामुळेच जमिनीस समांतर अशा टेबलाच्या पृष्ठावर थोडे पाणी टाकले, तर ते लवकर सर्व बाजूंस पसरते पण मध टाकला तर तो पसरावयाला जास्त वेळ लागतो.

बाहेरील प्रेरणा असतील (किंवा नसतील) अशा, स्थितीत असणारी द्रायूची समतोल अवस्था किंवा गतिमान अवस्था यांचा अभ्यास द्रायुयामिकीत होतो. अभियांत्रिकीतील व्यावहारिक उपयोजनांमुळे द्रायुयामिकीला अनन्यसाधारण महत्त्व प्राप्त झाले आहे किंबहुना द्रायुयामिकी ही अभियांत्रिकीचीच एक शाखा आहे असेदेखील मानले जाते.

द्रायूची गती व गतिनियमन करणाऱ्या स्थितीचे अध्ययन आणि उपयोजन यांचा अंतर्भाव या शास्त्रात होतो. द्रायुयामिकी या संज्ञेत द्रायुस्थितिकी, द्रायुशुध्दगतिकी आणि द्रायुगतिकी यांचा समावेश आहे. द्रायुस्थितिकीमध्ये स्थिर द्रायूंचा अभ्यास, द्रायुशुध्दगतिकीमध्ये गतिमान द्रायूचा व द्रायुप्रवाहाचा भूमितीविषयक अभ्यास म्हणजे वेग सदिश, प्रवेग सदिश, संवेग सदिश, अभिसरण, प्रवाहरेषा, प्रवाहाचे प्रकार इत्यादींचा अभ्यास आणि द्रायूगतिकीमध्ये गतिमान द्रायूवरील प्रेरणांसंबंधीच्या अभ्यासाचा अंतर्भाव होतो. त्यांशिवाय द्रायुयामिकीमध्ये विशेष अवस्थेतील द्रायूंच्या अभ्यासविभागांना वेगळ्या संज्ञा देण्याची प्रथा आहे. द्रविकीमध्ये पाणी व इतर तत्सम द्रवांचा अभ्यास, संकोच्य द्रायुशास्त्रामध्ये संकोच्य हवा व वायू यांचा अभ्यास, वायुगतिकीमध्ये वायूंचा गतिविषयक अभ्यास केला जातो. वायुगतिकी व वायुस्थितिकी यांविषयीची विशेष माहिती ‘वायुयामिकी’ या स्वतंत्र नोंदीत दिलेली आहे.

द्रायुयामिकीची मूलभूत तत्त्वे विज्ञान व अभियांत्रिकी विषयांतील कित्येक भिन्न शाखांना उपयोगी पडणारी आहेत. उदा, जल स्थापत्य, वातावरणविज्ञान, महासागरविज्ञान, उच्चतर वातावरणविज्ञान, द्रव्य अभियांत्रिकी, वैमानिकी अभियांत्रिकी, नाविक अभियांत्रिकी इत्यादी. थोडक्यात म्हणजे गतिमान किंवा स्थिर द्रायूशी संबंधित असलेल्या सर्व व्यवसायांत आणि तत्संबंधी उद्‌भवणाऱ्या नवीन समस्यांना, उदा., ⇨चुंबकीय द्रवगतिकी, चुंबकीय वायुगतिकी, वंगण, आघात तरंग, विक्षोभ, आयन द्रायुयामिकी [→ आयनद्रायु भौतिकी] इत्यादींना शास्त्रीय बैठक उपलब्ध करून देणे यांचा अंतर्भाव द्रायुयामिकीत होतो.

द्रायुयामिकीचा उष्मागतिकीशी (उष्णता आणि यांत्रिक व इतर स्वरूपाच्या ऊर्जा यांच्यातील संबंधांचे गणितीय विवरण करणाऱ्या शास्त्राशी) निकटतम संबंध आहे म्हणूनच प्रसंगी औष्णिक संवाहकता विचारात घ्यावी लागते. विशेषतः वायूची स्थिती तापमानावर अवलंबून असते. तथापि औष्णिक विषय ऊष्मागतिकी आणि उष्णता संक्रमण शास्त्रांत विशेष अभ्यासले जातात. त्याचप्रमाणे वायुयामिकीचा देखील स्वतंत्र विचार केला असल्याने संबंधित गोष्टी ‘उष्मागतिकी’ व ‘वायुयामिकी’ या नोंदींत पहाव्यात.

इतिहास :द्रायुयामिकीचे मूळ द्रवस्थितिकी, द्रव अभियांत्रिकी व द्रवगतिकी या शाखांच्या प्रारंभीच्या विकासात आढळते. यांपैकी मुख्यत्वे स्थिर स्थितीतील पाण्याचा अभ्यास करणाऱ्या द्रवस्थितीकी या शाखेचा विकास प्रथम झाला. या विकासात आर्किमिडीज (इ. स. पू. सु. २८७ –२१२) या ग्रीक शास्त्रज्ञांपासून ते ब्लेझ पास्काल (१६२३–६२) या फ्रेंच शास्त्रज्ञांपर्यंत अनेक शास्त्रज्ञांनी महत्त्वाची कामगिरी केली. श्यानता व स्थितिस्थापकता (लावलेली प्रेरणा काढून घेतल्यानंतर पदार्थ मूळ स्थितीत येण्याचा गुणधर्म) यांसारख्या द्रायूंच्या गुणधर्मांमुळे द्रायुप्रवाहाचा अभ्यास करणे अतिशय गुंतागुंतीचे होत असल्याने गतिमान द्रायूंच्या शास्त्राची प्रगती मात्र अनेक शतके खुंटली होती. यामुळे या शास्त्राच्या बाबतीत प्रगतीची वाटचाल दोन मार्गांनी झाली. द्रव अभियंत्यांनी पाण्याचा वापर व त्याचे नियंत्रण करण्यासाठी बांधकामे करताना आपल्या व्यावहारिक अनुभवाचा आधार घेतला आणि अशा प्रकारे जे ज्ञान संकलित झाले त्याला ‘आनुभविक द्रव अभियांत्रिकी’ असे नामाभिधान प्राप्त झाले. या शाखेचा इतिहास ग्रीक व रोमन संस्कृतींपासून सुरू होत असला, तरी खऱ्या अर्थाने लिओनार्दो दा व्हींची (१४५२–१५१९) यांच्याकडे तिचे जनकत्व जाते. फ्रेंच ॲकॅडमी ऑफ सायन्सेसचे आद्य संस्थापक एद्न माऱ्यॉत यांचा द्रायूतील घर्षणासंबंधी एक ग्रंथ १६८६ मध्ये प्रसिद्ध झाला या ग्रंथात त्यांनी द्रवयामिकीचे काही सिद्धांत व अनुप्रयोग यांचे विवेचन केलेले होते. नळाच्या मजबुतीच्या मापनासंबंधीही काही प्रायोगिक माहिती त्यांनी दिलेली होती.

अठराव्या व एकोणिसाव्या शतकांतील अनेक शास्त्रज्ञांनी आणि गणितज्ञांनी, विशेषतः डानिएल बेर्नुली व लेनर्ड ऑयलर यांनी दुसरा मार्ग स्वीकारला. त्यांनी वास्तव द्रायूऐवजी आदर्श द्रायूच्या गुणधर्मांचा अभ्यास करणाऱ्या शाखेचा विकास केला. श्यानता, स्थितिस्थापकता व पृष्ठताण हे वास्तव द्रायूंचे गुणधर्म विचारात न घेणाऱ्या या शाखेला ‘सैद्धांतिक द्रवगतिकी’ असे नाव मिळाले. बेर्नुली यांचे समीकरण द्रायूंना लागू केलेल्या ऊर्जेच्या अविनाशित्वाच्या तत्त्वाचे उत्तम उदाहरण आहे. या समीकरणाचा विस्मयजनक प्रायोगिक पडताळाही मिळालेला आहे. ई. ए. टोरिचेल्ली, न्यूटन, सी. एल, एम् एच् नेव्हिअर, जी. जी. स्टोक्स, जे. सी. बॉर्दा, डब्ल्यू. फ्रूड, ई. माख, एल्. प्रांट्ल, जे. डब्ल्यू. रॅली, ओ रेनल्ड्झ. इ. शास्त्रज्ञांनी केलेल्या मूलभूत संशोधनामुळे या शास्त्रांच्या प्रगतीला मोठा हातभार लागलेला आहे.

एकोणिसाव्या आणि विसाव्या शतकांत आनुभविक व सैध्दांतिक शाखांचे एकत्रीकरण करणे शक्य झाले. या दृष्टीने फ्रूड, रेनल्ड्झ व रॅली यांसारख्या शास्त्रज्ञांनी विकसित केलेली प्रतिकृती व ⇨ परिमाणात्मक विश्लेषण यांची तंत्रे, प्रांट्ल यांचा सीमास्तरासंबंधीचा सिद्धांत, थीओडोर फोन कार्मन यांचा संक्षोभाचा सिद्धांत यांचे महत्त्व मोठे मानण्यात येते. सध्याही जगातील विविध प्रयोगशाळांत या शास्त्राच्या प्रगतीच्या दृष्टीने अनेक शास्त्रज्ञ संशोधन करीत आहेत.

प्रारंभिक संकल्पना : द्रायुयामिकी या शास्त्रातील प्रारंभिक संकल्पना म्हणजे द्रायुकण, द्रायूची घनता, द्रायूचे विशिष्ट गुरुत्व व विशिष्ट वजन, द्रायूचे विशिष्ट घनफळ, दाब प्रेरणा, द्रायुदाब, कर्तरी प्रेरणा, कर्तरी प्रतिबल, प्रदिश, संकोच्यता, श्यानता, पृष्ठताण इ. असून त्यांचे या ठिकाणी विवरण दिलेले आहे. तर वेग सदिश, प्रवेग सदिश या संकल्पना द्रायुशुद्धगतिकीमध्ये पुढे दिल्या आहेत.

द्रायुकण : कोणताही द्रायू हा रेणूंचा बनलेला असतो. या रेणूंच्या ऊष्मागतिकीय हालचाली एकसारख्या चालूच असतात. द्रायुकणाचे आकारमान इतके मोठे असावे लागते की, त्यामधील रेणूंच्या ऊष्मागतिकीय वेगांची सरासरी शून्य व्हावी परंतु हा द्रायुकण म्हणजे एखाद्या भूमितीय बिंदू मानता येईल इतपत त्याचे आकारमान लहानही असावयास हवे. द्रायुकणाच्या कल्पनेमुळे त्यांच्या रेणवीय संरचनेकडे दुर्लक्ष करून द्रायूही एक अखंड असे माध्यम आहे, असे मानता येते. त्याचप्रमाणे द्रायुप्रवाह हाही अखंड आहे, असे गृहीत धरता येते. द्रायुकणाची संकल्पना द्रायुयामिकीत फार उपयुक्त आहे.

द्रायूची घनता : (p). दर एकक घनफळात असणारे द्रायूचे वस्तुमान म्हणजे द्रायूची घनता होय.

द्रव, वायू, घन या कोणत्याही अवस्थेतील पदार्थाच्या रेणूला निश्चित वस्तुमान असल्याने घनता ही दर एकक घनफळात समाविष्ट होणाऱ्या रेणूंच्या संख्येच्या प्रमाणात असते.

वायू अवस्थेतील पदार्थाचे रेणुकण घन अथवा द्रव पदार्थांच्या रेणुकणांच्या तुलनेने एकमेकांपासून अधिक दूर असतात. म्हणून घन पदार्थ आणि द्रव पदार्थ यांची घनता वायू व बाष्प यांच्या घनतेहून जास्त असते.

विशिष्ट वजन : (वजनमान W) द्रायूचे विशिष्ट वजन (वजनमान) हे द्रायूच्या दर एकक घनफळाचे वजन होय. घनता आणि विशिष्ट वजन यांचा संबंध W = pg या समीकरणावरून मिळतो (g = गुरुत्वीय प्रवेग).

वायूचे विशिष्ट वजन हे वायूचे तापमान व दाब यांवर अवलंबून असते. वायूचे तापमान, दाब व विशिष्ट वजन यांचा संबंध पुढील समीकरणांनी दर्शविता येतो.

सामान्यतः आदर्श वायूसाठी P/RT – W  आणि समतापी (ज्यात व्यूहाचे तापमान स्थिर राहते अशा) प्रक्रियेत P/W =  स्थिरांक. येथे P = दाब, R = वायुस्थिरांक, T = निरपेक्ष तापमान.

विशिष्ट गुरुत्व : द्रवाचे अथवा घन पदार्थांचे विशिष्ट गुरुत्व म्हणजे पदार्थाची घनता व पाण्याची ४^° से. या प्रमाण तापमानातील घनता यांचे गुणोत्तर होय.

द्रवाचे अथवा घनाचे विशिष्ट गुरुत्व = पदार्थाची घनता / पाण्याची घनता.

वायूचे विशिष्ट गुरुत्व मात्र दोन वेगवेगळ्या सापेक्ष रीतींनी दर्शविले जाते आणि ते ठराविताना तापमान व दाब प्रमाणित मूल्याची असावी लागतात.

वायूचे विशिष्ट गुरुत्व = वायूची घनता / हायड्रोजनाची घनता

अथवा

वायूचे विशिष्ट गुरुत्व = वायूची घनता / हवेची घनता

प्रमाण तापमानासंबंधी एकवाक्यता दिसून येत नाही. भौतिकीविज्ञ ४^° से. तापमान प्रमाण मानतात, तर अभियंते १५^° से. तापमान प्रमाण मानतात. प्रमाण दाब किंवा दाब म्हणजे पाऱ्याच्या ७६·० सेंमी. उंचीच्या स्तंभाचा दाब होय. म्हणूनच प्रमाण तापमान व प्रमाण दाब यांचा स्पष्ट उल्लेख करणे आवश्यक असते.

विशिष्ट घनफळ : द्रायूच्या एकक वस्तूमानाचे घनफळ म्हणजे द्रायूचे विशिष्ट घनफळ होय. वायूचे विशिष्ट घनफळ ठराविताना दाब व तापनाम प्रमाण मूल्याची असणे आवश्यक आहे.

दाब प्रेरणा: एका द्रायुबिंदूतून जाणारे कोणतेही प्रतल घेतले व त्यावरील प्रेरणेचा अभ्यास केला, तर ही प्रेरणा परिणामतः त्या प्रतलाला तिर्यक् असते परंतु दाब प्रेरणेचा त्या प्रतलामधील किंवा प्रतलाला समांतर असणारा घटक दुर्बल असतो व प्रलंब घटक अधिक बलवान असतो. प्रेरणेच्या या प्रतलाला समांतर असणाऱ्या घटकास कर्तरी प्रेरणा म्हणतात. कर्तरी प्रेरणा प्रतलाला स्पर्शीय असते.

द्रायूचा दाब : द्रायुबिंदूच्या स्थानातून जाणाऱ्या कोणत्याही प्रतलावर प्रती एकक क्षेत्रफळावर लंब दिशेने कार्य करणारी प्रेरणा म्हणजे त्या बिंदूवरील द्रायुदाब होय.

स्थिर द्रायू आणि आदर्श द्रायू यांमध्ये द्रायुदाब द्रायूतील कोणत्याही प्रतलास लंबरूपच असतो, म्हणजेच तो सर्व दिशांना सारखाच असतो.

द्रायुदाब दर चौ. सेंमी. वर P किग्रॅ. अथवा डाइन प्रती चौ. सेंमी. या एककांत व्यक्त केला जातो. द्रायुदाब हा केवल दाब किंवा गेज दाब या दोन प्रकारच्या राशींनी व्यक्त केला जातो. केवल दाब म्हणजे विशिष्ट ठिकाणचा एकूण दाब किंवा विशिष्ट ठिकाणचा दाब उणे संपूर्ण रिक्ततेमधील (निर्वातातील) दाब होय. वातावरणीय दाब नेहमी केवल दाबाच्या स्वरूपातच दिला जातो. गेज दाब म्हणजे त्या ठिकाणचा केवल दाब व भोवतालचा वातावरणीय दाब यांच्यामधील फरक होय. द्रायुयामिकीत सामान्यतः दाब हा गेज दाब याच स्वरूपात दिला जातो.

गेज = केवल दाब – भोवतालचा वातावरणीय दाब.

संकोच्यता : द्रायूची संकोच्यता ही घनफळ-स्थितिस्थापकता गुणांकाच्या व्यस्तांकाने दर्शविली जाते. घनफळ-स्थितिस्थापकता गुणांक (E_v)

E_v = – V · dp/dV

या सूत्रावरून मिळतो. येथे V = घनफळ, dV = V चा अवकल, p= दाब, dp = p चा अवकल (अवकलाच्या स्पष्टीकरणासाठी ‘अवकलन व समाकलन’ ही नोंद पहावी).

संकोच्यता = 1/E_v = – 1/V · dV/dp

वायूचा घनफळ-स्थितिस्थापकता गुणांक समतापी प्रक्रियेत p आणि असंक्रमी (ज्यात व्यूहामध्ये बदल होत असताना त्यातून उष्णता बाहेर जाऊ दिली जात नाही अगर त्यात उष्णता बाहेरून प्रवेश करू शकत नाही अशा) प्रक्रियेत rP असतो.

येथे C_p = स्थिर दाब असतानाची विशिष्ट उष्णता, C_v = स्थिर आयतन असतानाची विशिष्ट उष्णता [→ उष्णता ऊष्मागतिकी].

श्यानता : दोन लगतच्या थरांमधील सापेक्ष गती, कर्तरी प्रेरणा (ज्या प्रेरणेमुळे पदार्थांतील समांतर प्रतले समांतरच राहतात पण सापेक्षतः स्वतःच्या दिशेला समांतर अशी विस्थापित होतात अशी प्रेरणा) किंवा कोणीय विरूपण यांना प्रतिरोध करण्याच्या द्रायूच्या गुणधर्मास श्यानता म्हणतात व या गुणधर्मामुळे द्रायूत आंतरिक कर्तरी प्रतिबल उत्पन्न होते. द्रायूंमध्ये श्यानता हा गुणधर्म द्रायू गतिमान असतानाच प्रत्ययाला येतो.

श्यानतेची व्याख्या माख यांनी अधिक सुस्पष्ट केलेली आहे. मोठ्या आकारमानाच्या दोन समांतर फलकांमधील अंतर Y अल्प असून त्यामधील जागा द्रायूने व्याप्त आहे (आ.१). त्यांपैकी एक फलक स्थिर आहे व दुसरा फलक F या प्रेरणेमुळे U या अल्प वेगाने पुढे सरकत आहे. प्रत्येक फलकाच्या पृष्ठभागावरील द्रायुकण फलकाला चिकटून राहतील असे गृहीत धरल्यास अंतर (Y) आणि वेग (U) अल्प असल्यामुळे वेग वृद्धिफलन (वेगातील वाढ दर्शविणारी गणितीय राशी) रैखिक किंवा एकघाती असेल. स्थिर फलकांवरील द्रायुकणांचा वेग शून्य असेल व सरकत्या फलकांवरील द्रायुकणांचा वेग U असेल आणि मधल्या स्तरांतील द्रायुकणांचा वेग स्तरांच्या क्रमानुसार शून्यापासून U पर्यंत वाढत जाईल म्हणजेच द्रायूचे स्तर जणू काही एकावर एक असे पुढे सरकत आहेत असे मानता येईल. पुष्कळ द्रायूंच्या बाबतीत अनुभवाने असे सिद्ध झाले आहे की, द्रायूच्या दोन निकटच्या स्तरांमधील कर्तरी प्रतिबल (T) न्यूटन यांच्या पुढील सूत्रानुसार मिळू शकते.

T = μ · dU/dY

येथे dU हा वेगाचा अवकल व dY फलकांमधील अंतराचा अवकल होय आणि μ हा श्यानता गुणांक आहे (श्यानता गुणांकाला श्यानता व गतिकीय श्यानता अशा पर्यायी संज्ञा प्रचलित आहेत).

द्रायूचे कर्तरी प्रतिबल कोणीय विरूपणाच्या त्वरेच्या म्हणजेच dU/dY च्या प्रमाणात असते, हा न्यूटन यांचा नियम होय (घन पदार्थातील कर्तरी प्रतिबल विरूपणाच्याच सम प्रमाणात असते, हे लक्षात ठेवले पाहिजे).

न्यूटन यांचा श्यानतेचा नियम ज्या द्रायूंना लागू पडतो त्या द्रायूंना न्यूटोनीय द्रायू म्हणतात ( ‘द्रायूंचे वर्गीकरण’ या उपशीर्षकाखालील विवरण पहावे). ज्यांना तो लागू पडत नाही त्यांना अन्यूटोनीय द्रायू असे म्हणतात.

शुद्धगतिकीय श्यानता : द्रायूची शुध्दगतिकीय श्यानता (V) म्हणजे द्रायूची श्यानता व द्रायूची घनता यांचे गुणोत्तर होय.

शुद्धगतिकीय श्यानता = द्रायूची श्यानता  / द्रायूची घनता

म्हणजेच v = μ /p

शुद्धगतिकीय श्यानता ‘स्टोक्स’ या एककात मोजली जाते, तर श्यानता ‘पॉइज’ या एककात मोजली जाते [→ श्यानता].

स्थिर द्रायू व आदर्श द्रायू यांची श्यानता शून्य असते. श्यानता शून्य द्रायूंना अश्यान द्रायू असे संबोधतात.

 

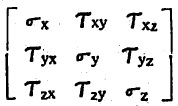प्रतिबल प्रदिश : द्रायुकणावरील पृष्ठप्रतिबल (एकक क्षेत्रफळावर कार्य करणारी प्रेरणा), प्रतल समांतर घटक व प्रलंब घटक पुढे दिलेल्या प्रदिशाच्या योगे दर्शविता येतात (प्रदिश या संज्ञेच्या स्पष्टीकरणासाठी ‘प्रदिश’ ही नोंद पहावी).

 

 

या प्रदिशात x हा x– अक्षाच्या दिशेतील प्रलंब घटक, तर T_xy हा x– अक्षाशी लंबप्रतलावर म्हणजे yz प्रतलावरील y– अक्षाच्या दिशेतील कर्तरी घटक व त्याचप्रमाणे इतर चिन्हांचा अर्थ आहे. स्थिर व आदर्श द्रायूंसाठी कर्तरी घटक शून्य असल्याने प्रतिबल प्रदिश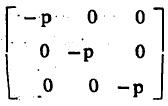 असा होतो. (p = द्रायूस्थितियकी दाब).

पृष्ठताण व कैशिकता : द्रायुकणांतील संलग्नतेमुळे द्रायूत पृष्ठताण उत्पन्न होतो. ताणप्रेरणांना प्रतिरोध करण्याच्या द्रवाच्या गुणधर्माला संलग्नता म्हणतात, तर इतर पदार्थांना चिकटून राहण्याच्या द्रवाच्या गुणधर्माला आसंगता म्हणतात. संलग्नता व आसंगता यांमुळे द्रवाला कशिकता हा गुणधर्म येतो. जेव्हा आसंगतेपेक्षा द्रायूची संलग्नता जास्त असते तेव्हा द्रायू केशनलिकेत खाली उतरतात. आसंगता अधिक असेल, तर ते केशनलिकेत वर चढतात. त्यायोगे केशनलिकेतील द्रवाचे पृष्ठदेखील अनुक्रमे बहीर्वक्र व अंतर्वक्र बनते [→ कैशिकता पृष्ठताण].

औष्णिक संवाहकता : एकक जाडी असलेल्या दोन पृष्ठांमधील तापमानाचा फरक एकक असता, एकक क्षेत्रफळातून एका सेकंदात वाहणाऱ्या उष्णतेला त्या पदार्थांची औष्णिक संवाहकता म्हणतात. संकलित उष्णता संवहन सूत्र असे लिहिता येईल.

q = kA(T₁–T₂)/1

येथे k = औष्णिक संवाहकता, A = क्षेत्रफळ, दोन बाजूंच्या तापमानांतील फरक, q = प्रती सेकंदात वाहणारी उष्णता = दोन बाजूंमधील अंतर.

द्रायूंचे वर्गीकरण : आदर्श द्रायू व वास्तव द्रायू असे द्रायूंचे दोन विभाग मानता येतील.

आदर्श द्रायू : असंकोच्य व अश्यान द्रायूला आदर्श द्रायू असे म्हणतात. आदर्श द्रायू प्रत्यक्षात अस्तित्वात नाहीत, तरीदेखील शास्त्रीय विवेचनात आसन्नीकरणाने (बहुशः) द्रायू आदर्श आहेत असे गृहीत धरणे बऱ्याच वेळा सोयीचे ठरते. आदर्श द्रायूच्या बाबतीत कर्तरी प्रतिबल व श्यानता शून्य असते. आदर्श द्रायूतील कोणत्याही प्रतलावरील प्रतिबल त्या प्रतलाला पूर्णपणे लंबरूप असते. आदर्श द्रायूचा दाब सर्व दिशांना सारखाच असतो. स्थिर द्रायू आणि अश्यान द्रायूंना हा नियम लागू पडतो. आदर्श द्रायू ही केवळ सैद्धांतिक कल्पना आहे. आदर्श द्रायूला परिपूर्ण द्रायू असेदेखील म्हणतात.

संपूर्ण वायुरूप अवस्थेत हवा व इतर वायूंचे गुणधर्म व अभिलक्षणे आदर्श द्रायूप्रमाणे असतात. आदर्श वायूच्या एकक वस्तुमानासाठी स्थिती समीकरण  PV = RT/m असे आहे. येथे P = दाब, V = घनफळ R = वायूस्थिरांक, T = निरपेक्ष तापमान आणि m = रेणूभार स्थिति [→ समीकरण].

वास्तव द्रायू : आदर्श द्रायूची सैद्धांतिक संकल्पना प्रत्यक्षात अस्तित्वात असणाऱ्या द्रायूंना नेहमी उपयोगी पडत असते असे नाही. वास्तव द्रायूचे वर्गिकरम पुढील प्रमाणे करता येईस.

श्यान द्रायू : ज्या द्रायूतील कर्तर विरूपण त्वरा ही केवळ त्यावरील कर्तरी प्रेरणेवर अवलंबून असते असे द्रायू. यात न्यूटोनीय व अन्यूटोनीय असे दोन प्रकार आहेत. न्यूटोनीय द्रायूचे कर्तरी प्रतिबल हे कर्तर त्वरेच्या सम प्रमाणात असते. अशा द्रायूची श्यानता एक स्थिरांक असते. अन्यूटोनीय द्रायूचे कर्तरी प्रतिबल हे कर्तर त्वरेचे फलन (गणितीय रीत्या संबंधित असलेले) असते परंतु हे फलन रैखिक नसते. अन्यूटोनीय द्रायूची श्यानता स्थिर नसते. सामान्यपणे ज्या द्रायूंना न्यूटन यांचा श्यानतेचा नियम लागू पडत नाही त्या द्रायूंना अन्यूटोनीय द्रायू म्हणतात.

कालावलंबी द्रायू : काही द्रायूंना कर्तर प्रेरणा लावून ठेवली असता त्यांची श्यानता हळूहळू कमी होत जाते (उदा., तैल रंग, टूथपेस्ट, मध, छापण्याची शाई) किंवा वाढत जाते. म्हणजे त्यांची श्यानता ही त्यावर किती काळ कर्तर प्रेरणा लागू होती यांवर अवलंबून असते, अशा द्रायूंना कालावलंबी द्रायू असे म्हणतात. व्यवहारात या प्रकारचे द्रायू अनेकदा उपयोगात येतात म्हणून त्यांचा विचार करणे आवश्यक आहे.

श्यान-स्थितिस्थापक द्रायू : ह्या वर्गातील द्रायूंचे कर्तरी प्रतिबल हे कर्तर त्वरा व विरूपण यांचे फलन असते.

संमिश्र द्रायू : हे वर उल्लेख केलेल्या प्रकारांचे मिश्रण होय.

चुंबकीय द्रायू : ह्या प्रकारातील द्रायूंचे कर्तरी प्रतिबल हे कर्तर त्वरा व चुंबकीय क्षेत्र यांवर अवलंबून असते.

आणखी एक प्रकार म्हणजे काही द्रायूंच्या विवेचनात ते विभक्त द्रायूकणांचे बनलेले आहेत असेच मानावे लागते आणि त्या द्रायूंचे अखंडत्व गृहीत धरणे योग्य ठरत नाही. म्हणजेच त्यांच्या बाबतीत द्रायुकणांची कल्पना लागू पडत नाही.

वास्तव वायूचे स्थिती समीकरण मिळविणे बिकट असते. त्यांचे गुणधर्म प्रत्यक्ष प्रयोगाने व अनुभवसिद्ध सूत्रांवरून मिळवावे लागतात. उदा. उच्च दाब व कमी तापमानाला वायूची लक्षणे द्रवाशी जवळची असतात. अशा वायूसाठी व्हॅन डर व्हाल्स यांचे स्थितिदर्शक समीकरण

P = (RT/V_n–b)–(a/V_n²)

प्रसिद्ध आहे. येथे a, b हे स्थिरांक प्रत्यक्ष प्रयोगाद्वारे निश्चित केले जातात. V_n = रेणवीय विशिष्ट घनफळ, R = वायूस्थिरांक, P = दाब, T = निरपेक्ष तापमान [→ स्थिती समीकरण].

द्रायुस्थितिकी 

या शास्त्रात स्थिर द्रायूमधील बिंदूस्थलावरील दाब व त्यातील बदल आणि त्यांना स्पर्श करणाऱ्या पृष्ठावरील द्रायुदाब, प्रेरणा इत्यादींचा अभ्यास करतात. स्थिर द्रायूचे अभिलक्षण आदर्श द्रायूप्रमाणे असल्याने द्रायुकणांतून जाणाऱ्या कोणत्याही अत्यल्प क्षेत्रफळ A वर कार्य करणारी लंबरूप प्रेरणा F असल्यास त्या स्थलाचा द्रायुदाब म्हणजे

सीमा	F
A⟶0	A

ही सीमा होय. (‘सीमा’ या संकल्पनेसाठी ‘अवकलन’ व ‘समाकलन’ ही नोंद पहावी).

स्थिर द्रायूमध्ये कोणत्याही बिंदूच्या ठायी सर्व दिशांना सारखाच दाब असतो. आदर्श द्रायू गतिमान असले, तरी त्यांना हा नियम लागू पडतो.

ब्लेझ पास्काल यांचा नियम : स्थिर द्रायूच्या मुक्त पृष्ठावरील तसेच स्थिर द्रायूच्या कोणत्याही बिंदूवर दिलेला जादा दाब स्थिर द्रायूच्या सर्व भागांवर कोणतीही कमतरता न येता सारखाच प्रेषित होतो, ह्या तत्त्वाचा उपयोग द्रवीय उत्थापक (हॉइस्ट), द्रवीय ऊर्जासंचायक, द्रवीय दाबयंत्र, द्रवीय गतिरोधक आदी द्रवीय यंत्रांत केला जातो [→ द्रविकी दाबयंत्र].

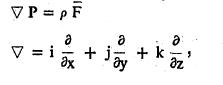द्रायुदाब समीकरण : स्थिर द्रायूतील सूक्ष्म अंतरावरील दोन बिंदूवरील द्रायुदाब समीकरण येथे अवकलकारक देकार्तीय सहनिर्देशकात, p = द्रायूची घनता,F‾ बाह्य प्रेरणा. (‘अवकलकारक’ या संज्ञेच्या स्पष्टीकरणार्थ ‘कारक सिध्दांत’ ही नोंद पहावी).

द्रायू केवळ गुरुत्वाकर्षणीय क्षेत्रात आहे आणि Z– अक्ष उदग्र (उभा) आहे, असे मानल्यास द्रायुदाब समीकरणाच्या समाकलनावरून आपण  P = – gpz +c असे दाबाचे फलन मिळवू शकतो (c = समाकलन स्थिरांक). त्यावरून समदाबाचे पृष्ठतल हे क्षैतिज (क्षितिजसमांतर) प्रतल असते आणि द्रायुदाब हा खोलीच्या प्रमाणात असतो हे लक्षात येईल.

संकोच्य द्रायूंच्या म्हणजेच वायूंच्या स्थितिकीय अभ्यासात ऊष्मागतिकीय समीकरणे विचारात घ्यावी लागतात. उदा., आदर्श द्रायूसाठी स्थिती समीकरण P = kp (k = स्थिरांक) असे घेतल्यास दाब समीकरणाच्या समाकलनावरून आपणास P = C_e^gz / k (c = समाकलन स्थिरांक, e = स्वाभाविक लॉगरिथमाचा आधारांक) असे समीकरण मिळते.

पृष्ठावरील रेटा व दाबकेंद्रे : द्रवाला स्पर्श करणाऱ्या परिमित पृष्ठावरील कोणत्याही ठिकाणी द्रव दाबाचा रेटा त्या पृष्ठावर अवलंबून असतो. सर्व दाब प्रेरणांची निष्पन्न प्रेरणा ठरविण्याकरिता तिचे परिणाम व कार्यरेषा ठरविणे आवश्यक असते.

क्षैतिज पृष्ठावरील रेट्याचे परिमाण gphA (g = गुरुत्वीय प्रवेग, p = द्रायूची घनता, h = पृष्ठाची मुक्त प्रतलापासूनची खोली, A = पृष्ठाचे क्षेत्रफळ) असते आणि ती दाब प्रेरणा किंवा रेटा त्या क्षेत्राच्या ⇨ गुरुत्वमध्यातून क्षेत्रास लंबरूप म्हणजे उदग्र, अधोमुख कार्य करते. ही प्रेरणा ज्या बिंदूवर लागू होते त्याला दाबकेंद्र म्हणतात. येथे त्या पृष्ठाचा गुरुत्वमध्य हाच दाबकेंद्र असतो परंतु तिर्यक् पृष्ठावरील निष्पन्न रेट्याचे परिमाण पृष्ठाचे क्षेत्रफळ व पृष्ठाच्या गुरुत्वमध्यावरील दाब यांच्या गुणाकाराबरोबर असते. हा निष्पन्न रेटा पृष्ठाच्या ज्या बिंदुतून जाईल त्या बिंदूस दाबकेंद्र म्हणतात. तिर्यक् पृष्ठाच्या बाबतीत पृष्ठाचा गुरुत्वमध्य व दाबकेंद्र हे बिंदू वेगळे येतात.

वक्रपृष्ठावरील रेटा काढण्यासाठी प्रथम त्या पृष्ठाची अत्यल्प क्षेत्रफळ असलेल्या लहान लहान तुकड्यांत विभागणी केली आहे, अशी कल्पना करतात. यांपैकी कोणत्याही एका (dA क्षेत्रफळाच्या) तुकड्यावरील रेटा त्याला प्रलंब दिशेने असून त्याचे मूल्य dA·P असेल. या ‘मूल रेट्याचे’ OX, OY व OZ या तीन अक्षांच्या दिशांचे घटक काढतात. याप्रमाणे प्रत्येक तुकड्याच्या बाबतीत करून मग समाकलनाने सर्व OX ला समांतर घटकांची बेरीज F_x काढतात. त्याचप्रमाणे F_y, F_z काढून या तिघांच्या सदिश बेरजेवरून त्या वक्रपृष्ठावर कार्य करणारा निष्पन्न रेटा मिळेल.

उत्प्रणोदन व उत्प्रणोदन केंद्र : स्थिर द्रवामध्ये (किंवा वायूमध्ये) अर्धवट किंवा पूर्णपणे निमज्जित केलेल्या (बुडविलेल्या) घन पदार्थावरील निष्पन्न द्रायुप्रेरणा उदग्र व ऊर्ध्वाभिमुख असते, तिला उत्प्रणोदन असे म्हणतात. उत्प्रणोदन प्रेरणेचे परिमाण पदार्थाच्या निमज्जित भागाने स्थानांतरित केलेल्या द्रवाच्या वजनाइतके असते व ती नेहमी या स्थानांतरित द्रवाच्या वस्तुमान मध्यामधून कार्य करते. या स्थानांतरित द्रवाच्या वस्तुमान मध्याला उत्प्रणोदन केंद्र असे म्हणतात.

आर्किमिडीज तत्त्व : स्थिर द्रवात पदार्थ बुडविला असता त्यावरील उद्धरण प्रेरणा स्थानांतरित द्रवाच्या वजनाएवढी असते आणि द्रवात तरंगणारा पदार्थ त्याच्या वजनाइतके द्रव स्थानांतरित करतो. हे तत्त्व प्रथम आर्किमिडीज यांनी मांडले. आर्किमिडीज तत्त्वाचे अनेक उपयोग आहेत. घन पदार्थाचे घनफळ काढण्यासाठी विशिष्ठ वजन माहीत असलेल्या द्रवात तो पदार्थ संपूर्ण बुडवून त्याचे द्रवातील वजन घेतात. पदार्थाचे हवेतील वजन (W₁) व द्रवातील वजन (W₂) आणि द्रवाचे विशिष्ठ वजन (W) यांवरून पदार्थाचे घनफळ V = W₁–W₂/w असे मिळते. द्रव पदार्थाचे विशिष्ठ गुरुत्व काढण्यासाठी देखील ह्या तत्त्वाचा उपयोग होतो. तरकाट्याच्या साहाय्याने आपणास द्रव पदार्थाचे विशिष्ट गुरुत्व तात्काळ मोजता येते. तरकाटा आर्किमीडीज तत्त्वावरच आधारलेला आहे [→ घनतामापक].

समतोलाचे स्थिरत्व : तरंगणाऱ्या घन पदार्थाचे उदग्र दिशेतील समतोलत्व नेहमी स्थिरच असते, कारण तो पदार्थ खाली दाबून किंवा वर ओढून सोडला, तरी तो पुन्हा पूर्व स्थितीस येतो. त्याचप्रमाणे तरंगणाऱ्या पदार्थाचे अल्प कोणीय विस्थापन केल्यास आणि त्या पदार्थाचा गुरुत्वमध्य G हा उध्दरण केंद्र H च्या खाली असल्यास परिवलनामुळे उत्पन्न होणारे प्रेरणायुग्म नेहमी पदार्थाला पूर्व स्थितीस नेणारे असते व परिवलन–समतोल स्थिर असतो परंतु उद्धरण केंद्र गुरुत्वमध्याच्या खाली असल्यास काही विशिष्ठ परिस्थितीतच समतोल स्थिर असू शकतो.

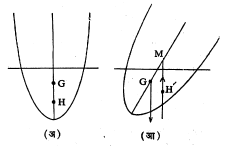
उपप्लव केंद्र : (आ.२). अल्प परिवलनामुळे उद्धरण केंद्राची नवीन स्थिती जी H’ तीमधून जाणारी उदग्र रेषा HG रेषेला ज्या M ह्या बिंदूत छेदते त्या बिंदूस उपप्लव केंद्र म्हणतात. अल्प परिवलनामुळे निस्सारीत (बाजूला सारलेल्या) द्रवाचे घनफळ बदलत नाही असे गृहीत धरल्यास स्थिर, तटस्थ व अस्थिर समतोलासाठी HM &gt HG, HM = HG, HM·HM &lt HG असल्यास थोडे तिरके झालेले जहाज पूर्णपणे कलंडेल. जहाज बांधताना त्याचा समतोल स्थिर असण्यासाठी उपप्लव केंद्र शक्य तितके जास्त उंचावर घेणे इष्ट असते परंतु ते जास्त उंच झाल्यास समुद्र खवळलेला असताना जहाजाला हेलकावे जास्त बसतात याचाही विचार करावा लागतो.

द्रवस्थितीकीच्या अनुप्रयुक्तीची स्थळे : द्रव्य साठविण्याच्या टाक्या, पाण्याखालील बोगदे, पाणी सोडण्याची दारे, धरणाच्या भिंती, पाणी अडविण्याकरिता मारलेल्या मेखा, दाब मोजण्याची साधने, द्रवीय दाबयंत्रे, द्रवीय ऊर्जासंचायक, द्रवीय उत्थापक, द्रवीय नियंत्रक यंत्रे, द्रवीय गतिरोधक वगैरे द्रवस्थितिकीच्या अनुप्रयुक्तींची योजना स्थळे होत. वायुस्थितीकीसंबंधीच्या विवरणाकरिता ‘वायुयामिकी’ ही नोंद पहावी.

द्रायुशुद्धगतिकी

द्रायुयामिकीमध्ये द्रायुप्रवाहाच्या अभ्यासासाठी दोन पध्दती आहेत. एक जे. एल्. लाग्रांझ यांची व दुसरी ऑयलर यांची. लाग्रांझ पध्दतीत द्रायूतील कोणताही एक द्रायुकण घेऊन तो कसा वाहतो, त्याचा मार्ग, वेग, प्रवेग इत्यादींचा अभ्यास केला जातो तर ऑयलर पध्दतीत एकाच स्थळी म्हणजे एकाच बिंदूपाशी राहून त्या बिंदूतून जाणारा द्रायुप्रवाह अभ्यासला जातो.

प्रवाहानुगामी किंवा विशिष्ट कण अवकलकारक :

येथे Vx,Vy, Vz, V‾ चे देकार्तीय घटक होत.

वरील समीकरणाने दिल्या जाणाऱ्या D/Dt या कारकाला प्रवाहानुगामी अवकालकारक किंवा विशिष्ट कण अवकलकारक असे म्हणतात. याचा उपयोग द्रायुयामिकीमध्ये अनेक ठिकाणी होतो. समजा b ही (दाब, घनता, वेग यांसारखी) विशिष्ट द्रायुकणाशी निगडित राशी आहे मग वरील कारकाच्या संयोगाने

असे अवकल समीकरण मिळते. b हा वेग असल्यास Db / Dt वरून त्या द्रायुकणाचा प्रवेग मिळेल. b हा संवेग (वस्तुमान X वेग ही राशी) असल्यास वरून त्या कणावरील प्रेरणा मिळेल इत्यादी.

पथरेषा, प्रवाहरेषा व प्रवाहनलिका: कुठल्याही द्रायुकणाने आक्रमिलेल्या मार्गाला पथरेषा म्हणतात. द्रायूमधील ज्या रेषेवरील कुठल्याही बिंदूतून काढलेली स्पर्शिका ही द्रायुकणाची त्या ठिकाणच्या गतीची दिशा दर्शविते, त्या रेषेस प्रवाहरेषा म्हणतात. अशा एकमेकींलगतच्या अनेक प्रवाहरेषांच्या समूहाला प्रवाहनलिका म्हणतात. प्रवाहरेषेच्या व्याख्येवरून असे लक्षात येते की, विशिष्ट प्रवाहनलिकेतून वाहणारा प्रवाह त्याच प्रवाहनलिकेतून अखेरपर्यंत वाहत रहातो. प्रवाहनलिकेची कक्षा सोडून तो बाहेर जाऊ शकत नाही.

द्रायुप्रवाहांचे वर्गीकरण : संथ प्रवाह : (स्थिर प्रवाह). द्रायूत कुठल्याही बिंदूपाशी द्रायूचा प्रवाह काळानुसार बदलत नाही म्हणजेच सर्व क्षणी प्रवाहाचे एकूण स्वरूप कायम रहात असेल, तर तो प्रवाह संथ किंवा स्थिर आहे असे म्हणतात. उलट एकाच स्थळी काळानुसार बदलणाऱ्या प्रवाहास अस्थिर प्रवाह म्हणतात.

एकसम प्रवाह : द्रायूतील प्रवाह सर्व ठिकाणी एकाच वेळी एकसारखाच असेल, तर तो एकसम प्रवाह आहे असे म्हणतात व तसा नसेल, तर त्याला विषम प्रवाह म्हणतात.

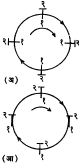घूर्णनी (परिभ्रमी)व अधूर्णनी (अपरिभ्रमी)प्रवाह : द्रायुप्रवाहातील प्रत्येक अतिसूक्ष्म कण जर आपआपल्या अक्षाभोवती फिरत असेल, तर त्या प्रवाहाला घूर्णनी प्रवाह असे म्हणतात. घूर्णनी प्रवाहात प्रत्येक कणाची दिशा अवकाशात एकसारखी बदलत जाते (आ. ३ अ). अघूर्णनी प्रवाहात द्रायुकणांची दिशा बदलत नाही (आ. ३ आ). फक्त श्यानताजन्य प्रेरणाच द्रायुकणांना त्यांच्या अक्षाभोवती घूर्णन गती देऊ शकतात म्हणून श्यानतायुक्त किंवा वास्तव द्रायूमधील प्रवाह नेहमी घूर्णनी असतो. आदर्श द्रायू अश्यान असतो ( अशी कल्पना केलेली आहे) त्यामुळे त्यातील प्रवाह अघूर्णनी असतो.

अघूर्णनी प्रवाहातील वेग सदीश (ν‾)हा वेगवर्चस् फलनाच्या (Φच्या) वृद्धि फलनाने दिला जातो (ν‾= ν Φ)कारण घूर्णतासदिश या सदिश w‾= Δν‾ समीकरणाने दिला जातो. परंतु अघूर्णनी प्रवाहात w‾= 0 Δ*ν‾= 0 म्हणून सदिश नित्यसमीकरणानुसार

(Δ*Δ.Φ=0) ν‾ = ΔΦ

(येथे व खालील विवरणात आलेली ‘सदिश’ ही संज्ञा व त्यासंबंधीचे गणित यांच्या स्पष्टीकरणासाठी ‘सदिश’ ही नोंद पहावी.)

भोवरा (आवर्त) : एखाद्या स्थिर द्रायूमध्ये स्वतःच्या आसाभोवती परिभ्रमण (घूर्णन) करणारी वृत्तचिती घातल्यास वृत्तचितीच्या पृष्ठभागाजवळील द्रायू वृत्तचितीबरोबर त्याच वेगाने परिभ्रमण करू लागतो. वृत्तचितीपासून अंतर वाढेल तसा द्रायूचा वेग कमी होत जातो. म्हणजे परिभ्रमण करणाऱ्या वृत्तचितीपासूनचे अंतर व द्रायूचा वेग हे व्यस्त प्रमाणात असतात. अशा भ्रमणगतीला ‘मुक्त भोवरा’ असे म्हणतात.

भोवरी (आवर्ती) प्रवाहात वृत्तचितीची त्रिज्या कमी कमी करत ती सीमान्ती शून्य आहे असे समजले, तर रेषा-भोवरा (रेषा-आवर्त) मिळतो. कोनीय वेग (w) व द्रायूबिंदूचा वेग (v) यांचा संबंध ω = ∇ x v असा दर्शविता येतो.

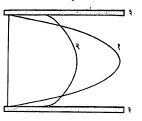
अभिसरण: द्रायूमधील घूर्णन गतीचे दिग्दर्शन करण्यासाठी अभिसरण (Γ) या राशीचा उपयोग होतो. द्रायुमध्ये कोणतीही बंद वक्ररेषा काढल्यास (आ.४) द्रायुवेगाचे वा वक्राभोवतीचे रेखा समाकलन [→ अवकलनव समाकलन] म्हणजे तेथील अभिसरण (Γ) होय.

परंतु सदिश समाकलनातील स्टोक्स यांच्या नियमानुसार

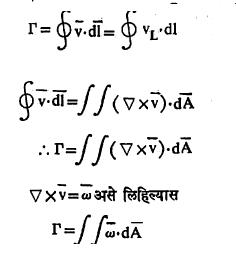
(येथे dA हा वक्राने सिमीत केलेल्या क्षेत्रफळाचा अत्यल्प भाग असून समाकलन या क्षेत्रफळावर करावयाचे आहे.) असे लिहिल्यास आदर्श द्रायूच्या बाबतीत अभिसरण स्थिर असते. प्रवाही अघूर्णनी असेल, तर अभिसरण शून्य होते. अघूर्णनी प्रवाह आपोपाप घूर्णनी होऊ शकत नाही तसेच घूर्णनी प्रवाह आपोपाप अघूर्णनी होऊ शकत नाही, हा विल्यम टॉमसन केल्व्हिन यांच्या घूर्णनी प्रवाहाच्या अक्षय्यत्वाचा सिद्धांत अत्यंत महत्त्वाचा आहे.

द्रायुगतिकी

द्रायुगतिकीमध्ये द्रायूवर कार्य करणाऱ्या प्रेरणा व त्यांचा गतिकीय परिणाम, द्रायूचा संवेग, ऊर्जा यांचा अभ्यास केला जातो.

द्रायुबिंदूवर तीन प्रकारच्या प्रेरणा कार्यप्रवण असू शकतात: (१) पृष्ठ प्रेरणा उदा., दाब प्रेरणा, श्यानता प्रेरणा इत्यादी. (२) बाह्य प्रेरणा उदा., गुरुत्वीय प्रेरणा, विद्युत चुंबकीय प्रेरणा. (३) कैशिकी प्रेरणा . द्रायुगतिकीच्या मुख्य नियमात (१) वस्तुमानाच्या अक्षय्यत्वाचा नियम, (२) न्यूटन यांचे गतिविषयक नियम (३) ऊष्मागतिकीचे नियम, (४) जे. सी. मँक्सवेल यांची विद्युत चुंबकीय समीकरणे हे महत्त्वाचे नियम येतात.

वस्तुमान अक्षय्यतेचा नियम : द्रायुचे वस्तुमान हे एक स्थिरांक असते. सूत्ररूपाने हा नियम DM / Dt = 0 (M = वस्तुमान) असा लिहीता येईल ( D/Dt हा प्रवाह अनुगामी अवकलकारक होय).

सातत्य समीकरण: वस्तुमानाच्या अक्षय्यतेच्या नियमावरून आपण असा निष्कर्ष काढू शकतो की, द्रायुप्रवाहामध्ये कोणताही V घनफळाचा विभाग घेतल्यास त्या विभागात ज्या तऱ्हेने (द्रायुचे) वस्तुमान आत येत असेल त्याच त्वरेने त्या विभागातील वस्तुमान वाढत जाईल. सूत्ररूपाने ही गोष्ट पुढीलप्रमाणे लिहिता येईल.

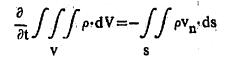
येथे p ही द्रायुची घनता, s हे V आकारमानाला सीमित करणाऱ्या पृष्ठभागाचे क्षेत्रफळ व V_n हा वेग सदिशाचा s ला लंबरूप घटक होय. यावरून गणित कृत्य करता

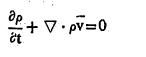
हे महत्त्वाचे समीकरण मिळते. याला सातत्य समीकरण असे म्हणतात. असंकोच्य वायूंसाठी p चे मूल्य स्थिर राहत असल्याने त्यांच्यासाठी सातत्य समीकरण

हे रूप धारण करते. प्रवाह अघूर्णनी असल्यास

तेव्हा असंकोच्य द्रायूच्या अघूर्णनी प्रवाहासाठी सातत्य समीकरण

या स्वरूपात येते.  Δ² φ या समीकरणाला लाप्लास समीकरण (पी, एस्‌. लाप्लास या फ्रेंच गणितज्ञांच्या नावावरून) असे म्हणतात. भौतिकीच्या अनेक शाखांत लाप्लास समीकरण उद्‌भवते (उदा., उष्णतेचे किंवा विद्युत् भारांचे संवहन). लाप्लास समीकरणाचा निर्वाह (उत्तर) काढणे सामान्यतः अवघड असते. केव्हा केव्हा एका शाखेतील अनुरूप आविष्काराशी तुलना करून दुसऱ्या शाखेतील निर्वाह काढता येतात.

एकमितीय प्रवाहासाठी सातत्य समीकरण Q = A·v = स्थिरांक या स्वरूपात मिळते. या ठिकाणी Q हे A क्षेत्रफळातून प्रती सेकंद वाहणाऱ्या द्रायूचे आकारमान आणि v हे वेग परिमाण होय.

कालवा, नलिका, नदी इत्यादींमधून वाहणाऱ्या असंकोच्य द्रायूच्या प्रवाहमानासाठी हे अत्यंत उपयोगी पडणारे सूत्र आहे.

न्यूटन यांचे गतिविषयक नियम वापरून संवेगाचा नियम, संवेग परिबलाचा (कोणीय वेग व निरूढी परिबल यांच्या गुणाकाराने मिळणाऱ्या राशीसंबंधीचा निरूढी परिबल हे कोणीय प्रवेगाला पदार्थाने केलेल्या विरोधाचे माप होय) नियम, श्यान द्रायूसाठी न्यूटन-स्टोक्स यांचा प्रतिबल-प्रतिविकृतीचा नियम व नेव्हिअर-स्टोक्स यांची गती समीकरण हे महत्त्वाचे नियम व समीकरणे मिळतात.

न्यूटन यांचा संवेगाचा नियम: द्रायूतील संवेगाचे प्रवाहानुगामी अवकलन द्रायूवर कार्य करणाऱ्या सर्व प्रकारच्या प्रेरणांच्या बेरजेएवढे असते. सदिश सूत्ररूपात हा नियम

असा लिहिता येईल. येथे F = प्रेरणा, v = वेग सदिश, dm = अल्पघटक वस्तुमान.

न्यूटन यांचा संवेगपरीबलाचा नियम : द्रायूतील संवेग परिबलाचे प्रवाहानुगामी अवकलन हे सर्व प्रेरणांच्या परिबलांच्या बेरजेइतके असते. (प्रेरणा व तिच्या कार्यरेषेचे दिलेल्या बिंदूपासूनचे लंबांतर यांच्या गुणाकाराला त्या प्रेरणेचे त्या बिंदूभोवतीचे परिबल म्हणतात). म्हणजे सूत्ररूपाने

न्यूटन यांनी असा नियम मांडला की, द्रायूतील श्यानताजन्य प्रतिबल हे कर्तरी प्रतिविकृतीच्या त्वरेच्या सम प्रमाणात असते परंतु आता असे दिसून आले आहे की, हा नियम अगदी थोड्या द्रायूनांच लागू पडतो व तोही प्रतिविकृतीची त्वरा फार नसेल तरच. परंतु काही गोष्टी गृहीत धरल्या, तर हा नियम सर्व वायूंना व बहुतेक सर्व द्रव्यांना लागू करता येतो, असे स्टोक्स यांनी दाखवून दिले. यासाठी आवश्यक असलेल्या गृहीतकांना स्टोक्स यांची गृहीतके म्हणतात. ही गृहीतके पुढीलप्रमाणे आहेत.

स्टोक्स यांची गृहीतके : (१) द्रायू समदिक् आहे म्हणजे त्याचे गुणधर्म सर्व दिशांनी सारखेच आहेत. (२) केवळ स्थानांतरण किंवा परिभ्रमण यामुळे विरोधी प्रतिबल निर्माण होऊ शकत नाही परंतु (द्रायूचे) विरूपण झाल्यास त्याला विरोध करणारी श्यानताजन्य प्रतिबले अस्तित्वात येतात. (३) प्रतिबल-विरूपण नियम द्रायूमध्ये सर्व दिशांनी सारखाच आहे. (४) (द्रायूमध्ये) विरूपण नसल्यास प्रतिबल प्रदिश हा आदर्श वायूमधील प्रतिबल प्रदिशाप्रमाणेच असेल.

या गृहीतकाच्या अनुरोधाने प्रतिबल-प्रतिविकृतीचा नियम पुढील समीकरणांच्या स्वरूपात देता येतो.

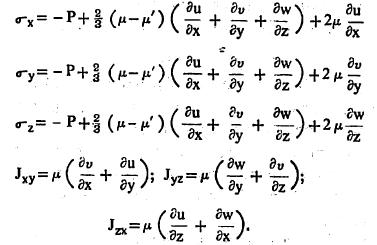
येथे u, v, w हे वेग सदिशाचे देकातींय घटक, P हा दाब आणि μ हा न्यूटन श्यानता गुणांक होय. μ ला ‘आकारमान-श्यानता गुणांक’ असे म्हणतात. असंकोच्य द्रायूसाठी μ′ चे मूल्य शून्य असते. द्रायूच्या आकारमाणात काही बदल झाला, तरच μ′ ला काही मूल्य येते.

नेव्हिअर-स्टोक्स यांची गती समीकरणे: श्यान द्रायूंच्या समस्यांची उकल आणि विश्लेषण करताना न्यूटन यांच्या गती नियमांवर आधारित असलेली नेव्हिअर-स्टोक्स यांची गती समीकरणे अत्यंत उपयोगी आहेत. स्थिर श्यानता असलेल्या असंकोच्य द्रायूसाठी

आणि अश्यान द्रायूसाठी (V = O) ती समीकरणे ऑयलर यांची गती समीकरणे म्हणून

अशी सुटसुटीतपणे लिहिता येतील. येथे V = वेग सदिश, F = बाह्य प्रेरणा, P = द्रायूची घनता, p = दाब, v = शुद्धगतिकीय श्यानता.

ही समीकरणे बहुघाती असल्याने ती सीमा अटी घेऊन सोडविणे हे अत्यंत अवघड कार्य आहे. काही गृहीतके धरून ही समीकरणे सोडविण्याचे पुष्कळ प्रयत्न झाले आहेत.

बेर्नुली समीकरण : (ऊर्जा समीकरण) द्रायूवर कार्य करणाऱ्या बाह्य प्रेरणा अघूर्णनी असतील, तर त्या वर्चस् फलनाच्या वृद्धिफलनाने व्यक्त करता येतील. सूत्ररूपाने

असे लिहिता येते. ऑयलर गती समीकरणाचे समाकलन विशिष्ट प्रवाह रेषेवरून केल्यास असंकोच्य द्रायूसाठी (विशिष्ट प्रवाह रेषेवरील) स्थिरांक, हे बेर्नुली समीकरण सहज मिळते.

द्रायूगतिकीत बाह्य प्रेरणा केवळ गुरूत्वीय आहे असे गृहीत धरून म्हणजे ψ = gh (g = गुरूत्वीय प्रवेग, h = द्रायुबिंदूची संदर्भ प्रतलापासून उंची) घेऊन बेर्नुली समीकरण

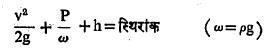
स्थिरांक असे प्रचलित रूपात लिहिता येते.

या सूत्राचा अर्थ असा की, द्रवाची एकूण ऊर्जा ही ऊर्जा-अक्षय्यतेच्या नियमानुसार स्थिरमूल्यी असते. एकक वस्तुमान द्रायूची ही गतिज ऊर्जा p/w ही दाब ऊर्जा व h ही स्थितिज ऊर्जा असल्याने या समीकरणास ऊर्जा समीकरण असेदेखील नाव आहे.

बेर्नुली सूत्रांचा उपयोग नलिका, नळ इत्यादींमधील द्रायुप्रवाह व ऊर्जेची घट काढण्यासाठी करता येतो. आ.५ वरून ही गोष्ट स्पष्ट होईल.

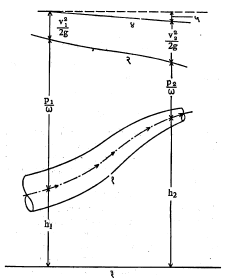
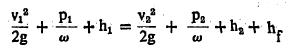
ऊर्जेचा विनाश होऊ शकत नाही, तर केवळ तिचे रूपांतर होऊ शकते. पदार्थाच्या ठिकाणी असलेल्या सर्व प्रकारच्या ऊर्जांची बेरीज स्थिरमूल्यी असते. वर वर्णिलेल्या बेर्नूली समीकरणांत औष्णिक ऊर्जा विचारात घेतली नाही.

स्तरीय प्रवाह व संक्षुब्ध प्रवाह : रेनल्ड्‌झ यांनी दायुप्रवाहांचे स्तरीय व संक्षुब्ध या दोन प्रकारांत वर्गीकरण केले आहे. प्रवाहातील सर्व द्रायुकण जर अत्यंत शिस्तबद्धतेने नियमित मार्गांवरून वाहत असतील, तर एकूण प्रवाह जणू काही द्रायूच्या पातळ अशा अनंत थरांचा बनलेला असतो. हे थर परस्परांवरून अलगद पुढे सरकत असतात. एका थरातील द्रायुकण दुसऱ्या थरात जात नाही, अशा प्रवाहाला स्तरीय प्रवाह म्हणतात.

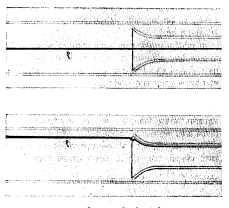
स्तरीय प्रवाह मिळण्यासाठी अनुकूल गोष्टी म्हणजे द्रायूची श्यानता जास्त असावी, वेग कमी असावा व प्रवाहमार्ग संकुचित असावा. स्तरीय प्रवाहात एखाद्या रंगीत द्रवाची बारिक धार (आ. ६ मध्ये १ या आकड्याने दर्शविलेली) सोडल्यास तिचे सरळ मार्ग दिसू शकतात, कारण स्तरीय प्रवाहात एकमेकींना छेदीत नाहीत. प्रवाह संक्षुब्ध झाला की ही रेषा आ. ७ मध्ये दाखविल्याप्रमाणे विसकटून जाते. आदर्श द्रायूला श्यानता नसल्याने त्याच्या प्रवाहाला घर्षणजन्य विरोध होत नाही. नळीतून अशा द्रायूचा स्तरीय प्रवाह जात असल्यास सर्व स्तरांचा वेग सारखाच असला पाहिजे (आ. ८ अ) परंतु वास्तव द्रायूंना श्यानता असते.

नळीतून त्यांचा स्तरीय प्रवाह चालू असेल, तर नळीच्या पृष्ठालगतच्या स्तराचा वेग शून्य असतो व तेथून जसजसे नळीच्या अक्षाकडे यावे तसतसा स्तरांचा वेग वाढत जातो. अशा प्रवाहाचे वेगवितरण आ. ८ (आ) मध्ये दाखविले आहे. स्तरीय प्रवाहाचा सरासरी वेग व त्यातील कमाल वेग यांचे गुणोत्तर सु.०·५ असते.

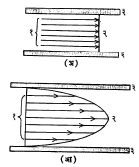संक्षुब्ध प्रवाह : संक्षुब्ध प्रवाहातील द्रायुकणांच्या गती अनियत किंवा स्वैर असतात. एका द्रायुकणाच्या वेगाचा इतर द्रायुकणांच्या वेगाशी काहीही संबंध नसतो. द्रायुकणांचे विशिष्ट असे थरच प्रस्थापित होत नाहीत. संक्षुब्ध प्रवाहातील द्रायुकणांमध्ये संवेग ऊर्जा, कर्तर प्रतिबल, उष्णता यांची देवाणघेवाण मुक्तपणे चालू असते. नळीमधील संक्षुब्ध प्रवाहातील एखाद्या द्रायुकणाचा मार्ग आ.९ (अ) मध्ये दाखविला असून आ. ९ (आ) मध्ये संक्षुब्ध प्रवाहाचे एकूण स्वरूप दिग्दर्शित केले आहे. प्रवाहात ॲल्युमिनियमाचे सूक्ष्मकण घालून त्यांची छायाचित्रे घेता येतात. अशा तऱ्हेने द्रवातील संक्षुब्ध प्रवाहाचे केलेले चित्रण आ. १० मध्ये दाखविले आहे.

घन कक्षांमधून (उदा., पाट, नळी) चालू असणाऱ्या संक्षुब्ध प्रवाहात घन कक्षेला लगत असा एक अगदी पातळ थर असतो. त्याला सीमास्तर म्हणतात. सीमास्तरातील प्रवाह हा स्तरीयच असतो. त्यानंतर जो एक थर येतो त्याला संक्रमण स्तर म्हणतात. या स्तरात, स्तरीय प्रवाहाचे हळूहळू संक्षुब्ध स्तरांत रूपांतर होत जाते. म्हणजे या स्तरातील प्रवाह संमिश्र असतो. या स्तरानंतर प्रवाहाचा मुख्य भाग येतो त्यातील प्रवाह पूर्णतया संक्षुब्ध असतो. आ. ११ मध्ये संक्षुब्ध स्तरातील वेगवितरण दाखविले आहे. त्यावरून असे दिसेल की, संक्षुब्ध प्रवाहाचा वेगवितरण वक्र, स्तरीय प्रवाहाच्या वक्राच्या तुलनेने जास्त चपटका असतो. सरासरी वेग आणि कमाल वेग यांचे गुणोत्तर ०·७४ (खडबडीत नळीसाठी) ते ०·८८ (अगदी गुळगुळीत नळीसाठी) येते. संक्षुब्ध प्रवाहात ऊर्जेचा व्यय (स्तरीय प्रवाहापेक्षा) जास्त होतो. संक्षुब्ध प्रवाहाला नळीचा विरोधही जास्त होतो. सामान्यतः नळीतील प्रवाहाच्या बाबतीत

द्रायूची घनता, μ = द्रायूची श्यानता)

या मितिहीन अंकाचे (त्याला रेनल्ड्झ अंक म्हणतात) मूल्य २,००० पेक्षा कमी असल्यास प्रवाह स्तरीय असतो व ३,००० पेक्षा जास्त असल्यास प्रवाह संक्षुब्ध बनतो.

रेनल्ड्‌झ अंक व इतर मितिहीन समूह : वरील विवेचनावरून असे दिसून येईल की, नळ्यांतील किंवा कालव्यांतील द्रायूच्या प्रवाहाचे स्वरूप रेनल्ड्झ अंकाच्या मूल्यावर अवलंबून असते. अशा ठिकाणी प्रवाहाचे स्वरूप मुख्यतः श्यानताजन्य प्रेरणांवरून निश्चित होते. कारण येथे इतर प्रेरणा (उदा., गुरुत्वाकर्षणीय, पृष्ठताणजन्य) त्यामानाने दुर्लक्षणीय असतात.

येथे L ही त्या विशिष्ट प्रवाहाशी निगडित अशी (कोणती तरी) लांबी आहे. नळीच्या बाबतीत L म्हणजे नळीचा व्यास होय. वरील समीकरणावरून हे लक्षात येईल की N_Re हा दोन प्रेरणांचे गुणोत्तर असल्याने तो एक मितिहीन प्रचल (विशिष्ट परिस्थितीत विशिष्ट स्थिर मूल्य असणारी राशी) किंवा शुद्ध आकडा आहे. त्यामुळे त्याचे मूल्य हे कोणत्याही मापन पद्धतीनुसार एकच येते. त्याचप्रमाणे प्रयोगातील संचाची सर्व मापे सारख्याच प्रमाणात बदलल्यास मितिहीन प्रचलाचे मूल्य बदलत नाही.

अभियांत्रिकीमधील कित्येक समीकरणे इतकी गुंतागुंतीची असतात की, त्यांचे सैद्धांतिक निर्वाह काढणे मुष्किल असते. अशा समीकरणातील प्रचलांची मितिहीन समूहात जुळणी केल्यास समीकरणाचे विश्लेषण करणे सोपे होते. कित्येकदा विशिष्ट अभियांत्रिकीय कूट प्रश्नाचे उत्तर मूळ संचाच्या प्रतिकृतीवर प्रयोग करूनच काढावे लागते. अशा वेळी मूळ संच व प्रतिकृती ही गतिकीय दृष्ट्या समरूप असावी लागतात. मूळ संच व प्रतिकृती यांचे त्या आविष्काराशी संबंधित मितिहीन समुह सममूल्य असतील, तर ही गोष्ट साध्य होते. या दृष्टीने पाहता जेथे जेथे वेगवितरण किंवा वेग श्यानतेवर अवलंबून असतो तेथे समरूप प्रतिकृती करताना रेनल्ड्झ अंक महत्त्वाचा ठरतो. उदा., प्रवाहाचे नियमन, जहाजे, पाणबुड्या वगैरेंच्या गतीला होणारा पाण्याचा विरोध मोजणे इत्यादी.

काही इतर मितिहीन समूह:

ऑयलर (पहिला) अंक:

येथे Δ P म्हणजे नळीच्या घर्षणामुळे दाबात होणारी  घट आहे नळ्यातून वाहणाऱ्या प्रवाहाला होणाऱ्या घर्षणजन्य विरोधाचा अभ्यास करताना याचा उपयोग होतो.

फ्रुड (दुसरा)अंक :

कालव , उघडी गटारे वगैरमधील प्रवाहाचा अभ्यास करताना याचा उपयोग होतो.

माख अंक : M किंवा N_Ma= v/C

येथे C म्हणजे त्या माध्यमातील ध्वनीचा वेग होय. जेथे द्रायूच्या संकोचामुळे निर्माण होणाऱ्या प्रेरणा जोरदार असतात तेथे या अंकाचा उपयोग होतो. माख अंक M हा ०·३ पेक्षा जास्त झाल्यास संकोचन प्रेरणा लक्षात घ्याव्या लागतात. M चे मूल्य १ पेक्षा कमी असल्यास प्रवाह अवस्वनी आहे असे म्हणतात. हा M &gt १ असल्यास स्वनातीत व M &gt ५ अतिस्वनातीत प्रवाह आहे असे म्हणतात.

जेथे पृष्ठताणजन्य प्रेरणा जोरदार असतात तेथे याचा उपयोग होतो. (डब्ल्यू. ई. वेबर या जर्मन भौतिकीविज्ञांच्या नावावरून हा अंक ओळखण्यात येतो).

या मितिहीन समूहांचे महत्त्व लक्षात येण्यासाठी जहाज बांधणीचे उदाहरण घेऊ. जहाजाच्या गतीला होणारा प्रतिरोध मुख्यत: दोन प्रकारे होतो : (१) घर्षणामुळे व (२) जहाजाच्या गतीमुळे ज्या निर्माण होतात त्यासाठी खर्च होणाऱ्या ऊर्जेपोटी. प्रत्यक्ष जहाजाची बांधणी करण्यापूर्वी त्याच्या लहान आकारमानाच्या प्रतिकृतींच्या (नमुन्यांच्या) चाचण्या घेऊन त्यावरून किमान प्रतिरोध होईल असा जहाजाचा आकार निवडतात; परंतु या प्रतिकृतीवरून निघणारे निष्कर्ष प्रत्यक्ष जहाजाला लागू पडतीलच याची खात्री कशी देता येईल ही समस्या उद्भवते. फ्रूड यांनी असे दाखवून दिले की, जहाज व याची प्रतिकृती यांचे भूमितीय आकार सारखेच असून रेनल्ड्झ अंकांची (vLρ/μ ; L = जहाजाची वा प्रतिकृतीची लांबी) मूल्ये एकच असतील, तर त्यांना होणारे घर्षणजन्य प्रतिरोध ठराविक पटीतच येतील. त्याचप्रमाणे दोहोंच्या बाबतीत फ्रूड अंकाची (v /√gL) मूल्ये एकच असतील, तर लाटांच्या आविष्कारामुळे होणारे प्रतिरोध ठराविक पटीतच येतील. या तत्त्वाचा उपयोग जहाजांच्या रचनाशास्त्रात [→ नाविक वास्तुशिल्प] मोठ्या प्रमाणावर केला जातो. विमानांच्या बांधणीबाबतही ही गोष्ट लागू आहे. धरणे, सांडपाण्याच्या निचऱ्याची व्यवस्था, बंदरामधील संरक्षक बांध वगैरेंची योग्य ती रचना ठरवितानाही त्या मितिहीन समूहांचा उपयोग होतो.

सीमास्तर व सीमास्तरीय प्रवाह : ज्या वेळी एखाद्या घन पदार्थाचा पृष्ठभाग व त्याच्या संपर्कात येणारा द्रायू यांच्यामध्ये सापेक्ष गती असते तेव्हा घनपृष्ठाच्या लगत द्रायूचा एक थर बनतो, त्याला सीमास्तर असे म्हणतात व त्या थरातील द्रायुप्रवाहाला सीमास्तरीय प्रवाह असे म्हणतात. या स्तराचे अभिलक्षण म्हणजे त्यातील द्रायूची गती (श्यानता प्रेरणेमुळे) रुद्ध (कमी) झालेली असते. सीमास्तराची संकल्पना प्रथम प्रांट्ल यांनी १९०४ मध्ये मांडली.

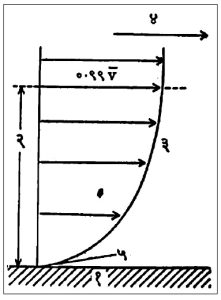
घनपृष्ठाच्या अगदी लगत द्रायूचा वेग शून्य असतो व तेथून तो वाढत जाऊन अनंतवर्तीपणाने (तत्त्वत: अनंत अंतरावर) मुक्त द्रायुवेगाइतका होतो. सीमापृष्ठापासून ज्या अंतरावर द्रायुवेग. मुक्त द्रायुवेगाच्या ९९% इतका होतो त्या अंतराला सीमास्तराची जाडी (d) असे म्हणतात. या जाडीचे मूल्यमुक्त द्रायुवेग, द्रायूची श्यानता, संबंधित घनपृष्ठाचा खडबडीतपणा व त्याचा द्रायुप्रवाहाला संलग्न होऊन गेलेला विस्तार या गोष्टींवर अवलंबून असते. आ. १२ मध्ये सीमास्तरातील वेगवितरण दाखविले आहे.

नळ्या, कालवे यांच्यामधून वाहतो तेव्हाही त्यांच्या घनपृष्ठावर सीमास्तर निर्माण होतात. पाण्यातून जाणारी पाणबुडी किंवा हवेतून जाणारे विमान यासारखा एखादा घन पदार्थ जेव्हा द्रायूतून जात असतो तेव्हा त्याच्याभोवती सीमास्तराचे एक आवरणच तयार होते. त्या पदार्थाला होणारा श्यानताजन्य प्रतिरोध हा या सीमा-स्तरातच उत्पन्न होतो. किंबहुना या प्रतिरोधाचे सैद्धांतिक विश्लेषण करता येण्यासाठीच सीमास्तराची कल्पना प्रथम उदयाला आली व पुढे ती प्रयोगांच्या कसोटीलाही उतरली.

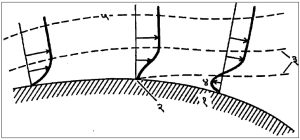
पृथग्भवन : बदलत्या आकाररेषेच्या पृष्ठावरून जेव्हा द्रायुप्रवाह वाहत असतो तेव्हा सीमास्तराची जाडी वाढत जाते. घनपृष्ठालगतच्या स्तरांचे वेग अधिक प्रमाणात कमीकमी होत जातात व त्यामुळे तेथील दाब वाढतो. या वाढत्या दाबामुळे शेवटी अशी परिस्थिती येते की, घनपृष्ठालगत द्रायूचा प्रवाह मुक्त द्रायुप्रवाहाच्या उलट दिशेने वाहू लागतो आणि द्रायुप्रवाह व घनपृष्ठ परस्परांपासून अलग होतात. त्या दोहोंमध्ये फट निर्माण होते. या आविष्काराला पृथग्भवन असे म्हणतात. आ. १३ मध्ये पृथग्भवन कसे उत्पन्न होते ते दाखविले आहे. आ. १४ मध्ये वृत्तचितीवरून पाणी वाहत असताना प्रवाहाचे झालेले पृथग्भवन व त्यापलीकडे निर्माण झालेला भोवरा दाखविला आहे. प्रवाहात ॲल्युमिनियमाचे बारीक कण घालून प्रवाहाचे स्वरूप दृश्यमान केले आहे.

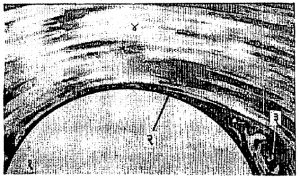
पृथग्भवनामुळे सामान्यत: प्रवाहाला होणारा प्रतिरोध वाढतो. विमानाच्या पंखांवरील उद्धरण प्रेरणा कमी होते. नळ, कालवे, गटारे यांतील प्रवाहमान कमी होते. त्याचप्रमाणे पंप, टरबाइन, विमानांचे पंखे (प्रचालक) यांसारख्या द्रायुगतिकीय साधनांची कार्यक्षमता कमी होते. नळातून  किंवा कालव्यातून पृथग्भवन होते तेथे झीज आणि धूप जास्त होतात. पंपाच्या व पंख्यांच्या पात्यावरही असेच परिणाम होऊ शकतात. या सर्व गोष्टींमुळे पृथग्भवन होऊ न देणे महत्त्वाचे असते. सीमास्तरामधील प्रवाह स्तरीय किंवा संक्षुब्धही असू शकतो. हा प्रवाह संक्षुब्ध झाल्यास प्रवाहाला होणारा प्रतिरोध वाढतो. प्रवाह संक्षुब्ध होणे हे रेनल्ड्झ अंकाच्या मूल्यावर अवलंबून राहते. संक्षुब्ध सीमास्तराबद्दलचा सैद्धांतिक अभ्यास अद्याप अपूर्णच आहे.

कोटरीभवन : द्रवाच्या प्रवाहात कोठे कोठे द्रायुगतिकीय कारणाने दाब इतका कमी होतो की, तो त्या द्रवाच्या बाष्पदाबाइतका किंवा त्याच्याही खाली जातो. अशा वेळी द्रवाचे बाष्पीभवन होऊन त्याचे बारीक बुडबुडे बनू लागतात. दाब कमी झाल्यामुळे द्रवात विरघळलेला वायू मुक्त होतो व त्याचेही बुडबुडे बनतात. या आविष्काराला कोटरीभवन हे नाव आहे. द्रवात घन पदार्थाचे बारीक कण निलंबित झालेले (लोंबकळत्या स्थितीत) असतील, तर कोटरीभवन जास्त सुलभतेने होऊ शकते (द्रव उकळणे हा सुद्धा एक कोटरीभवनाचाच प्रकार आहे; पण तेथे द्रवाला बाहेरून उष्णता देऊन कोटरीभवन होत असते). सीमास्तरांच्या पृथग्भवनाबरोबर अनेकदा कोटरीभवनही होते.

कोटरीभवनामुळे तयार होणारे बुडबुडे कित्येकदा अत्यंत अल्पकालात (काही मिलिसेकंदांत) तयार होतात. हा प्रकार काहीसा स्फोटासारखाच असतो. मग ते बुडबुडे फुटतात. अशा परिस्थितीत प्रचंड दाब निर्माण होतो. वातावरणीय दाबाच्या १२,००० पट पर्यंत असे दाब निर्माण झालेले आढळले आहेत.

कोटरीभवनामुळे आवाज निर्माण होतो. यंत्रसामग्रीत कंप निर्माण होतो व द्रायुगतिकीय साधनांची कार्यक्षमता एकदम कमी होते.

फुटणाऱ्या बुडबुड्यांच्या संपर्कात आलेल्या पोलाद किंवा काँक्रीट यांच्यासारख्या वस्तूंनाही नुकसान पोहोचते. आ. १५ मध्ये याप्रकारे काँक्रीटच्या भिंतींना झालेली इजा दर्शविली आहे.

द्रवगतिकीय साधनांची रचना करताना कोटरीभवन कसे टळेल याचा विचार करणे आवश्यक असते. जहाजांचे पंखे, टरबाइन पंप यांची रचना, अग्निबाणांच्या द्रव इंधनांचे वहन, वैद्यकशास्त्र अशा विविध क्षेत्रांत कोटरीभवनाची दखल घ्यावी लागते.

कर्षण प्रेरणा व प्रवाहरेखन : द्रायूमधून जाणाऱ्या घन पदार्थांच्या गतीला विरोध करणाऱ्या प्रेरणांना कर्षण प्रेरणा असे नाव आहे. कर्षण प्रेरणा कमीत कमी होण्यासाठी गतिमान पदार्थाची आकाररेषा सुयोग्य अशी करणे म्हणजेच प्रवाहरेखन होय.

कर्षण प्रेरणा चार प्रकारच्या असतात : (१) त्वक्घर्षण, (२) दाबजन्य कर्षण, (३) तरंग कर्षण आणि (४) प्रवर्तित कर्षण.

त्वक्घर्षणजन्य कर्षण द्रायूच्या श्यानतेमुळे उत्पन्न होते. अल्प श्यानत  असलेल्या हवा किंवा पाणी यासारख्या द्रायूमधील गतीच्या बाबतीत त्वक्घर्षण फक्त सीमास्तरातन उत्पन्न होते. द्रायूच्या श्यानतेमुळे घनपृष्ठावर ज्या कर्तर प्रेरणा उत्पन्न होतात त्यामुळे त्वक्घर्षण निर्माण होते.

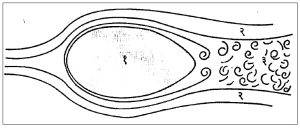
विशिष्ट परिस्थितीत सीमास्तराचे पृथग्भवन होऊन गतिमान पदार्थांच्या मागील भागात अनुप्रवाह निर्माण होतो. या अनुप्रवाहात भोवरे असतात (आ. १६). वस्तूच्या पुढील भागापेक्षा या अनुप्रवाहातील दाब कमी असतो. त्यामुळे वस्तूवर वेगाला विरुद्ध अशी जी प्रेरणा निर्माण होते तीच दाबजन्य कर्षण होय. या प्रेरणेसाठीही माध्यमाला श्यानता असणे आवश्यक असते. वस्तूची आकाररेषा यथायोग्य बनवून पृथग्भवन टाळता येते. अनुप्रवाहाचा विस्तारही कमी करता येतो. त्यामुळे दाबजन्य कर्षण कमी होऊ शकते. यासाठी सर्वसामान्य नियम स्थूलमानाने असा सांगता येईल की, वस्तूच्या पुढच्या भागाला गोलाई असावी तर मागचा भाग निमुळता असावा.

तरंग कर्षण प्रेरणा ध्वनीच्या वेगापेक्षा जास्त वेगाने जाणाऱ्या वस्तूंच्या बाबतीत प्रत्ययाला येते. उदा., स्वनातीत विमान हवेतून जाताना त्याच्या पुढच्या बाजूला हवेचे संपीडन (संकोचन) होऊन आघात तरंग निर्माण होतात, तर मधल्या भागापासून प्रसरण आघात तरंग निर्माण होतात. या तरंगनिर्मितीसाठी जरूर ती ऊर्जा गतिमान वस्तूकडूनच काढून घेतली जाते म्हणून तिची गतिज ऊर्जा कमी होते. ऊर्जेचा हा व्यय कर्षणामुळे होतो. या प्रकारचे कर्षण कमी होण्यासाठी वस्तूचे पुढील व मागील असे दोनही भाग टोकदार असावे लागतात. त्याचप्रमाणे वस्तूची जाडीही शक्य तितकी कमी असावी लागते.

विमानाच्या पंखावर जेव्हा द्रायुयामिकीय उद्धरण प्रेरणा कार्य करू लागते तेव्हा त्या प्रेरणेच्या वर्गाच्या प्रमाणात असणारी एक कर्षण प्रेरणा पंखावर कार्य करू लागते, हिला प्रवर्तित कर्षण असे म्हणतात.

असंकोच्य अश्यान द्वायू : असंकोच्य द्वायूची घनता स्थिर असते. द्रायूची श्यानता अल्प असल्यास तो अश्यान आहे असे मानले तरी चालते. अशा द्रायूशी संबंधित काही गोष्टींची चर्चा खाली केलेली आहे.

प्रवाह फलने : प्रवाहरेषेचे अवकल समीकरण dx/ V_x = dy/ V_y = dz/V_Z असे लिहिता येते.

येथे V_x, V_y, V_Z हे वेग सदिशाचे देकार्तीय घटक आहेत, या समीकरणाचे निर्वाह म्हणजे

f = f (x, y, z) = a

g = g (x, y, z) = b

(a व b हे स्थिरांक) ही दोन फलने मिळतात. ही फलने दोन पृष्ठकुले निर्देशित करतात. या पृष्ठकुलांच्या परस्परांशी होणाऱ्या छेदरेषा म्हणजे प्रवाहरेषा होत. या f व g फलनांना प्रवाह फलने असे म्हणतात. यांच्या साहाय्याने प्रवाहाचे एकूण स्वरूप व्यक्त करता येते. गणिताच्या साहाय्याने असे सिद्ध करता येते की,

‾V = ∇ f X ∇g (सदिश गुणाकार). संकोच्य द्रायूच्या बाबतीत हेच समीकरण ‾v = 1/ρ ∇ f X ∇g असे होते.

द्विमितीय प्रवाहाच्या अभ्यासात प्रवाह फलने विशेष उपयोगी पडतात. उदा., वेग सदिशाचा Z अक्षाच्या दिशेचा घटक शून्य असेल, तर तो X — Y पृष्ठातील द्विमितीय प्रवाह होतो. वेगसदिश X — Y प्रतलाला समांतर असेल, तर g = – z  व f ऐवजी ψ हे लाग्रांझ यांचे प्रवाह फलन होते. अघूर्णनी प्रवाहासाठी Y लाप्लास समीकरणाची पूर्तता करते म्हणजेच ∇²Ψ= 0.

ऊष्मागतिकीय परिणाम : आतापर्यंतच्या विवेचनात द्रायूत निर्माण होणारी किंवा संक्रमित होणारी उष्णता विचारात घेतली नाही; परंतु वास्तव द्रायूत ऊष्मागतिकीय परिणाम विचारात घ्यावे लागतात.

द्रायुप्रवाहातील एक अत्यल्प घनफळाचा विभाग विचारात घेतल्यास त्याला ऊष्मागतिकीचा पहिला नियम [→ ऊष्मागतिकी ] लावता पुढील समीकरण लिहिता येते.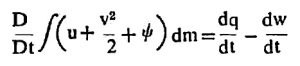

येथे dm = अल्प घटकाचे वस्तुमान, u = अंतर्गत ऊर्जा, φ = स्थितिज ऊर्जा, dq/dt = त्या विभागात येणाऱ्या निष्पन्न उष्णता ऊर्जेची त्वरा व dw/dt = त्या विभागावर सर्व प्रेरणांनी मिळून केलेल्या कार्याची त्वरा आहे.

त्याचप्रमाणे ऊष्मागतिकीचा दुसरा नियम लावता पुढील समीकरण मिळते.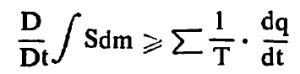

येथे S = एंट्रॉपी [→ एंट्रॉपी ] T= निरपेक्ष तापमान आहे.

प्रक्रिया व्युत्क्रमी (उलट दिशेनेही होणारी) असल्यास वरील समीकरणात = चिन्ह व व्युत्क्रमी नसल्यास > हे चिन्ह घ्यावे.

सामान्यत: घन कक्षांच्या लगतच्या प्रवाहातच उष्णतेचे परिणाम विचारात घ्यावे लागतात. इतरत्र प्रवाह सामान्यपणे समएंट्रॉपी असतो. आघात तरंगात किंवा सीमास्तरात श्यानतेमुळे उष्णतेचे उत्पादन होऊन एंट्रॉपी वाढते.

घनता व तापमान यांचा संबंध कॅलरीय स्थिती समीकरणाने दिला जातो.

ऊष्मागतिकीचा पहिला नियम संथ प्रवाही द्रायूसाठी dq = du + pd (1/ρ)

असा सुटसुटीतपणे लिहिता येतो.

येथे q = उष्णता, u = अंतर्गत ऊर्जा, p = दाब, ρ = द्रायूची घनता आहे. वरील समीकरणात रासायनिक ऊर्जा, विद्युत् ऊर्जा वगैरे इतर ऊर्जा विचारात घेतलेल्या नाहीत.

सूत्ररूपाने ऊष्मागतिकीचा दुसरा नियम

dq < Tds असा लिहिता येतो. येथे q = उष्णता, T = तापमान, S = एंट्रॉपी आहे. व्युत्क्रमी प्रक्रियेत dq = Tds असे लिहिता येते. या नियमाद्वारे एंट्रॉपीविषयी विवेचन करता येते.

द्रायुगतिकीतील एल्. क्रोको यांच्या प्रमेयावरून असा निष्कर्ष काढता येतो की, एंट्रॉपी व ऊष्मसंपत (पदार्थाच्या एकक वस्तुमानातील उष्णतेचा साठा; एंथाल्पी) सर्वत्र सम असलेला संथ प्रवाही घूर्णताशून्य असतो आणि घूर्णता उत्पन्न होण्यासाठी एंट्रॉपीची वृद्धी किंवा ऊष्मसंपताची वृद्धी व्हावी लागते.

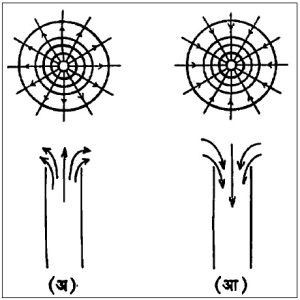
उगमस्थान : द्रायुप्रवाहातील बिंदूतून निघणारा प्रवाह सर्व दिशांनी अरीय व बहिर्मुख असेल तर तो बिंदू उगमस्थान म्हणून समजला जातो. उगमस्थानाभोवती कोणताही बंद पृष्ठभाग काढला आहे असे मानल्यास व त्या पृष्ठभागातून जाणारे प्रवाहमान 4πm असेल, तर उगमस्थानाचे बल m आहे असे मानतात. बिंदुमात्र उगमांपासून R या अंतरावर वेगवर्चस् फल Φ = m/R असते.

अरीय प्रवाह अंतर्मुख असेल, तर तो बिंदू लयस्थान म्हणून ओळखला जातो. लयस्थान म्हणजे ऋण उगमस्थान असे म्हणता येईल.

द्विक : सूक्ष्म अंतरावर (ds) असणारी सम बल असलेली उगमस्थान व लयस्थान यांची जोडी द्विक् म्हणून संबोधिली जाते. द्विकाची प्रबलता (m) 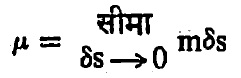ही सीमा होय.

लाप्लास समीकरण : असंकोच्य अश्यान द्रायूचा प्रवाह अवर्णनी असेल, तर सातत्य समीकरण हे लाप्लास समीकरण असते म्हणजे त्या प्रवाहाचे वर्चस् फलन f हे Ѳ f = 0 या समीकरणाची पूर्ती करते. देकार्तीय सहनिर्देशकांत हे समीकरण δ²Φ/ δ x² + δ²Φ/ δy² + δ²Φ/ δz² = 0 असे लिहिता येईल.

लाप्लास समीकरणाचा निर्वाह : लाप्लास समीकरणाच्या निर्वाहासाठी अनेक पद्धती आहेत. त्यांपैकी काही पद्धती पुढे वर्णिल्या आहेत.

चल पृथक्करण पद्धती : लाप्लास समीकरणाचे रूपांतर अनेक साध्या अवकल समीकरणांत करता येते. ध्रुवीय सहनिर्देशकांतील [⟶ भूमिती ] लाप्लास समीकरणावरून आपणास ए. एम्. लझांद्र यांचे अवकल समीकरण मिळते. त्या अवकल समीकरणाचा निर्वाह म्हणजे लझांद्र यांच्या बहुपदी होत. त्या दोन प्रकारच्या आहेत व ध्रुवीय सहनिर्देशकांतील लाप्लास समीकरणावरून एफ्. डब्ल्यू. बेसेल यांचे अवकल समीकरण मिळते. त्या समीकरणाचा निर्वाह ही बेसेल यांची प्रथम व द्वितीय प्रकारची फलने होत [→ अवकल समीकरणे; फलन].

प्रतिबिंबाची पद्धती : घन सीमापृष्ठावरून वाहणारा प्रवाह अघूर्णनी असेल व सीमापृष्ठांचा आकार सरळ, गोल किंवा वृत्तचिती असा भूमितीय असेल, तर तेथील प्रवाह वर्चस् काढण्यासाठी प्रतिबिंबाची पद्धती उपयोगी पडते. समजा अशा सीमापृष्ठाजवळ एखादे उगमस्थान (लयस्थान किंवा द्विक्) आहे. मग ते पृष्ठ जणू काही एक आरसाच मानून त्यात त्या उगमस्थानाचे प्रतिबिंब पडले आहे अशी कल्पना करावयाची. हे प्रतिबिंब असे असावे की, मूळ उगमस्थान व प्रतिबिंब यांच्या संयुक्त परिणामामुळे सीमापृष्ठावरील प्रवाहाची स्थिती प्रत्यक्षात आहे तशी व्हावी, मग त्या भागातील कोठल्याही बिंदूच्या ठिकाणी वेग वर्चस्, वेग सदिश इ. मूळ उगम व प्रतिबिंब यांच्या संयुक्त परिणामामुळे दिले जातील.

समाकल समीकरणाची पद्धती : या पद्धतीत ई. आय्. फ्रेडहोम समाकल समीकरणे येतात. सीमापृष्ठावरील वेगाचे पृष्ठाला लंब समाकल असलेले घटक ज्ञात असतील, तर ती नॉयमान समस्या (जॉन फोन नॉयमान यांच्या नावाने ओळखली जाणारी) व सीमापृष्ठावरील वेग वर्चस् फलने ज्ञात असतील, तर ती डीरिल्ले समस्या (पी. जी. एल्. डीरिक्ले यांच्या नावाने ओळखण्यात येणारी) होय. संख्यात्मक पद्धतीने या समस्या सोडविण्यासाठी संगणकाचे (गणकयंत्राचे) साहाय्य घेतले जाते. गणिती काटेकोरपणा काहीसा शिथिल करून निर्वाह काढण्याची संख्यात्मक पद्धती (शिथिलीकरण पद्धती) आर्. व्ही. साउथवेल यांनी काढली आहे. प्रवाह क्षेत्राचे प्रवाह रेषा व समवेग वर्चस् रेषा काढून जाळ्यासारखे विभाजन केले जाते. जाळ्यातील शिरोबिंदूवरील वेग वर्चसाचे सोयीस्कर असे अंदाजे मान सुरुवातीस गृहीत धरतात. सीमा अटी व लाप्लास समीकरणाचे सांत अंतरामधील [→ सांत अंतर कलन] स्वरूप वापरून पुढे ‘प्रयत्न आणि त्रुटीसुधार’ पद्धतीने वर्चस् फलनांचे आसन्नमान काढतात.

अनुरूपी चित्रण : द्विमितीय अघूर्णनी प्रवाहाविषयीच्या समस्यांकरिता ही एक अत्यंत प्रभावी पद्धती आहे. ही सदसत् फलन सिद्धांतात [→ फलन] अंतर्भूत होते. जी. एफ्. रीमान यांच्या प्रमेयानुसार विभागाच्या सीमांचे वैश्लेषिक फलनांनी वर्तुळात रूपांतर करता येते. जर अशी फलने सापडली, तर त्यावरून सीमाप्रवाहाचे रूपांतर अधिक सोप्या अशा वर्तुळाभोवतीच्या प्रवाहात करता येते. या पद्धतीतील प्रमुख अडचण म्हणजे संयुग्मी (ज्यांचा गुणाकार सत् आहे अशी) फलने निश्चित करणे ही होय.

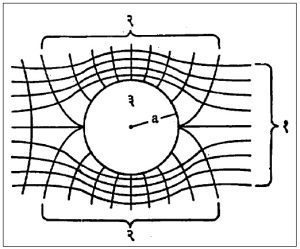
द्विमितीय अघूर्णनी प्रवाह आणि सदसत् फलन सिद्धांत : अघूर्णनी प्रवाहात वेग वर्चस् फलन Φ आणि प्रवाह फलन Ψ ही जात्य सदसत् संयुग्मी फलने होत. ती फलने कोशी-रीमान समीकरणांची (ए. एल्. कोशी व जी. एफ्. रीमान यांच्या नावांनी ओळखण्यात येणाऱ्या समीकरणांची) पूर्ती करतात. म्हणजेच δΦ/δx = δΨ/dy; δΦ/δy = – δΨ/δx अशी कोशी-रीमान समीकरणे मिळतात आणि म्हणूनच ही दोन्ही फलने लाप्लास समीकरणाची पूर्ती करतात.

वर्चस् फलन व प्रवाह फलन यांचे संयुक्तपणे आपणास एक सदसत् वर्चस् फलन ω = Φ + i ψ असे लिहिता येते ( i = √ – १). ही सदसत् वर्चस् फलने वैश्लेषिक फलने असतात. सदसत् वर्चस फलनांच्या अवकलनाद्वारे वेग प्रवेग आदी सदिश मिळू शकतात. सदसत् वर्चस् फलनांचा उपयोग घन पदार्थामुळे द्रायूत उत्पन्न होणारा संक्षोभ तसेच निरनिराळी प्रवाह क्षेत्रे यांच्या अभ्यासाकरिता चांगल्या प्रकारे होतो. पक्षकाच्या (कोणत्याही विरोधाला स्वत:च्या गतीच्या दिशेला प्रलंब दिशेत वायुगतिकीय उद्धरण प्रतिक्रिया उत्पन्न करेल असा आकार दिलेल्या वस्तूच्या; उदा., विमानाचा पंख) आकाराच्या अभ्यासासाठी अनुरूपी चित्रणाचा उपयोग महत्त्वाचा आहे. खालील उदाहरणांवरून सदसत् फलनांच्या उपयोगाची कल्पना येऊ शकेल.

द्रायूच्या एकसमप्रवाह क्षेत्रात वृत्तचितीच्या अडथळ्याने होणाऱ्या संक्षोभासाठी सदसत् वर्चस् फलन ω = – U (z + a²/z) (येथे z = x + iy; U = प्रवाहाचा वेग; a = वृत्तचितीची त्रिज्या) असे मिळते.

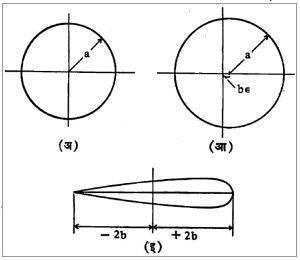
उत्तरोत्तर रूपांतरण पद्धती : रूपांतरण पद्धती वापरून काही समस्यांचे सुलभीकरण करता येते. उदा., सममित पक्षक-आकाराचा अभ्यास करताना अनुक्रमे :

Z = a · e^iθ

z = Z+ b ∈ e^iπ

Z’ = z + b²/z

अशी रूपांतरणे वापरून Z — प्रतलावरील a · e^iθ हे वर्तुळ Z’—  प्रतलावर सममिती पक्षक आकारात रूपांतरित करता येते (आ. १९).

Z’ = z + b²/z हे रूपांतरण एन्. ई. झुकॉव्हस्कई यांचे रूपांतरण म्हणून ओळखतात [→ वायुयामिकी]. टरबाइनांमधील पाती, विमानांचे पंख इत्यादींमध्ये सुयोग्य पक्षक-आकाराचे अनन्यसाधारण महत्त्व आहे.

एकमितीय प्रवाह : अभियांत्रिकीमध्ये एकमितीय प्रवाहाचा अभ्यास महत्त्वाचा असतो. नळ, कालवा, नाली, पाट, गटार इत्यादींमधून वाहणाऱ्या द्रायुप्रवाहाला एकमितीय प्रवाह समजता येईल. प्रस्तुत ठिकाणी आदर्श द्रायूसंबंधी माहिती दिली आहे. द्रायूच्या गती समीकरणावरून एकमितीय प्रवाहाची गती समीकरणे सहज मिळविता येतील. स्वतंत्रपणे देखील ही समीकरणे मिळविता येतात. नळातील द्रायुदाब सर्व ठिकाणी सारखा नसतो. उलट कालवा, नाली, गटारे इत्यादींमधील द्रव प्रवाह द्रायुमंडलीय दाबाखाली वाहत असतो. द्रव अभियांत्रिकीमध्ये नळ, कालवा इत्यादींमधून वाहणाऱ्या द्रवाचा अभ्यास करण्यात येतो.

प्रवाह प्रतिरोध : श्यानता या गुणधर्मामुळे द्रायुप्रवाहाच्या सर्व थरांत वेग एकसारखा नसतो. श्यानतेच्या परिणामाने द्रायूचा एक थर त्याच्या नजीकच्या दुसऱ्या थरावर कर्तरी प्रेरणा निर्माण करतो. यामुळे प्रवाहाला प्रतिरोध होतो.

द्रायू अश्यान आहे असे गृहीत धरले, तरीसुद्धा सीमास्तरांजवळील प्रवाहात द्रायूच्या आसंगतेमुळे द्रायूच्या प्रवाहाला प्रतिरोध होतो.

याशिवाय नळाचा आकारबदल, दिशाबदल, सांधा यांमुळे देखील प्रवाहास विरोध होतो. नळ, कालवे, गटारे इत्यादींची रचना करताना सर्व कारणांमुळे होणारा प्रवाह प्रतिरोध विचारात घ्यावा लागतो. प्रवाह प्रतिरोधामुळे ऊर्जेचा अपव्यय होतो आणि त्यामुळे नळातून अपेक्षित उंचीपर्यंत पाणी न चढणे किंवा गटारे तुंबणे यांसारखे त्रासदायक प्रकार उद्भवतात.

द्रवीय त्रिज्या : नळ, कालवा, पाट यांतील प्रवाहांसाठी द्रवीय त्रिज्या विचारात घ्यावी लागते. ही त्रिज्या नळाच्या अथवा कालव्याच्या काटछेदातील द्रव प्रवाहाचे क्षेत्रफळ आणि प्रवाहामुळे ओली होणारी छेदाची परिमिती यांचे गुणोत्तर होय.

द्रवीय त्रिज्या = प्रवाह क्षेत्रफळ / (काटच्छेदाची) ओली होणारी परिमिती

उदा., गोल नळाची द्रवीय त्रिज्या (R)

R = नळाची त्रिज्या / २ असते.

घर्षणांक : द्रायुप्रवाहाला घर्षणामुळे उत्पन्न होणारा प्रतिरोध अभिलक्षीत घर्षणांकाचा उपयोग करून मिळू शकतो. घर्षणांक हा प्रयोगाद्वारे अथवा अनुभवसिद्ध सूत्राद्वारे मिळविता येतो. उदा., नळातील स्तरीय प्रवाहासाठी घर्षणांक (f)

f = 64 / Re (Re = रेनल्ड्झ अंक)

ह्या सूत्राद्वारे मिळतो.

प्रवाह प्रतिरोधामुळे होणारा ऊर्जाक्षय : प्रवाह प्रतिरोधामुळे होणारात ऊर्जाक्षय काढण्यासाठी अनेक सूत्रे आहेत. या ऊर्जाक्षयामुळे नळातील  पाण्याच्या प्रवाहाचे जल वर्चस् कमी होते. जल वर्चसामधील घट (h_f) काढण्यासाठी एच्. डार्सी व जे. वाईस्बाख यांचे एक सूत्र आहे.

h_f = fLv² / 2gR

येथे f = डार्सी घर्षणांक, L = नळाची लांबी, v = द्रायूचा वेग, R = द्रवीय त्रिज्या आहे. कालव्यातील प्रवाहात होणाऱ्या जल वर्चसातील घट काढण्यासाठी आर्. मॅनिंग यांचे

h_f = n² Lv²/ R^4/3 असे एक सूत्र आहे.

येथे n चे मान सीमास्तराच्या खडबडीतपणानुसार घ्यावे लागते. उदा., मातीच्या कालव्यासाठी n = ०.०२२५.

रंध्र : रंध्रातून वाहणाऱ्या द्रवाचे प्रवाहमान रंध्राच्या आकारावर व रंध्राच्या वर द्रवाची उंची किती आहे यांवर अवलंबून असते. रंध्रातून द्रायू वाहत असताना द्रायूच्या धारेचा आकार प्रथम आकुंचित नंतर पुन्हा विस्तारीत असा) होतो, त्यास धारेचे आकुंचन म्हणतात.

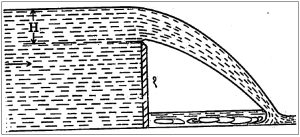
बंधिका : द्रवाच्या प्रवाहास विशेषत: पाण्याच्या प्रवाहात म्हणजे नदी, नाली, कालवे इत्यादींमध्ये आडव्या बंधिका (छोटा बंधारा) घालतात. बंधिकांची उंची कमी असल्यामुळे पाणी बंधिकांवरून वाहते. बंधिकेमुळे पाण्याची उंची वाढून त्याचा उपयोग अनुस्रोत प्रवाहातून पाटासाठी, कालव्यासाठी पाणी मिळण्यास होतो. कालव्यातील प्रवाहमापनामध्ये सुद्धा बंधिकांचा उपयोग करतात [→ द्रायुमापक]. बंधिकांचे आकारानुसार अनेक प्रकार आहेत. बंधिकेवरून वाहणाऱ्या पाण्याचे प्रवाहमान काढण्यासाठी अनेक सूत्रे आहेत. उदा., एच्.  बेझीन यांचे सूत्र

Q = 3.33 BH^3/2

(येथे B = बंधिकेवरील प्रवाहाची रुंदी, H = बंधिकेवरील पाण्याची उंची; आ. २०) वापरून पाण्याचे प्रवाहमान काढता येईल.

नाली कालवा : नाली किंवा कालव्यातील प्रवाहमापनासाठी प्रथम सूत्रावरून वेगाचे मान काढतात.

उदा., v = C √R ·S या सूत्रावरून प्रवाहाचा वेग मिळू शकतो.

(येथे v = वेग, C = कालव्याच्या खडबडीतपणावर अवलंबून असलेला गुणक, R = द्रवीय त्रिज्या, S = उताराच्या नत कोनाचे ‘ज्या’ गुणोत्तर). C या गुणकाचे मान काँक्रीट कालव्यासाठी १००, विटांच्या कालव्यासाठी ८५ वगैरे असते. प्रवाहमान काढण्यासाठी इतर महत्त्वाची सूत्रेदेखील उपलब्ध आहेत. उदा., मॅनिंग यांचे सूत्र

Q = 1.486 / n • R^2/3 • S^1/2 असे आहे.

n या गुणकाचे मान कालव्याच्या खडबडीतपणावर अवलंबून असते. N गुणकाचे मान काढण्यासाठी देखील सूत्रे आहेत.

कालव्याचा सर्वोत्तम आकार : कालव्याच्या काटच्छेदाचे क्षेत्रफळ दिले असता काटच्छेदाच्या ज्या आकारामुळे महत्तम प्रवाहमान मिळेल, तो त्याचा सर्वोत्तम आकार होय. उदा., आयताकार कालव्याच्या सर्वोत्तम आकारात खोलीच्या दुप्पट रुंदी असते.

कर्षण व उत्थापन : द्रायुप्रवाहातील कोणत्याही स्थिर वस्तूवर कार्य करणाऱ्या प्रेरणेचे दोन घटक मानता येतात. एक घटक प्रवाहाच्या  दिशेत असतो, तर दुसरा त्याला लंबरूप असतो. पहिल्या प्रकारचा घटक म्हणजे कर्षण प्रेरणा (F_D) होय व दुसऱ्या प्रकारच्या घटकाला उत्थापन प्रेरणा (F_L) म्हणतात. या दोन्ही प्रेरणांचे मान पुढील सूत्रांवरून मिळते.

F_D = C_D   ρ  a v²/2

F_L = C_L ρ a v²/2

येथे C_D, C_L हे स्थिरांक होत, r = द्रायूची घनता, a = घन पदार्थाच्या पृष्ठभागाचे क्षेत्रफळ, v = वेग.

कर्षण व उत्थापन प्रेरणा स्थिरांकांचे मान रेनल्ड्झ अंकावर अवलंबून असते.

कर्षण प्रेरणा ही वस्तूच्या दोन्ही बाजूंवरील दाबाच्या फरकामुळे किंवा प्रवाहाच्या श्यानजन्य कर्षणामुळे निर्माण होते. वस्तू प्रवाहरेखित असेल, तर कर्षण प्रेरणा कमी असते; परंतु प्रवाहरेखित वस्तू प्रवाहाच्या दिशेस थोडासा कोन करून असेल, तर उत्थापन प्रेरणा निर्माण होईल.

स्थिर लाट : पूर्णपणे बुडालेल्या बंधिकांवरून पाणी वाहताना विशिष्ट परिस्थितीत आ. २१ मध्ये दाखविल्याप्रमाणे उतरलेली पाण्याची पातळी अनुस्रोत बाजूस वाढते आणि त्या ठिकाणी स्थिर लाट [ अप्रगामी तरंग; ⟶ तरंग गति ] तयार होते. कालव्यातील प्रवाह मोजण्याकरिता कालव्याला विशिष्ट आकार देऊन मुद्दाम स्थिर लाट निर्माण करतात [→द्रायुमापक].

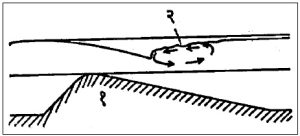
पुलाच्या स्तंभांतून पाणी वाहत जात असताना विशिष्ट परिस्थितीत अनुस्रोत बाजूला स्थिर लाट उत्पन्न होते (आ. २२).

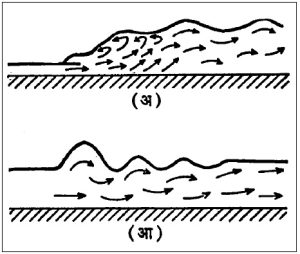
जलोच्छलन : वेगाने वाहणारा परंतु उथळ द्रव प्रवाह कमी वेगाने वाहणाऱ्या खोल द्रवास येऊन मिळतो, त्या वेळी द्रव संक्षुब्ध होऊन तो वर उसळतो. या आविष्कारास जलोच्छलन म्हणतात म्हणजे द्रव अधिक्रांतिक वेगातून अचानक उपक्रांतिक वेगात बदलतो व गतिज ऊर्जेचे रूपांतर हे स्थितिज ऊर्जेत होत असताना थोडासा ऊर्जाव्यय होतो. जलोच्छलन जास्त झाल्यास संक्षुब्ध असते व साधारण असल्यास ते स्थिर तरंग बनते.

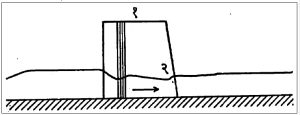
जलाघात : नळावरील झडप (व्हाल्व्ह) अचानक बंद केल्याने झडपेच्या प्रतिस्रोत व अनुस्रोत भागांत जलाघात म्हणजे प्रचंड दाबाची लाट निर्माण होण्याची शक्यता असते. झडप अचानक बंद झाल्यास म्हणजे संवेग अचानक रोधल्यास अनुस्रोत भागातील प्रवाहाच्या संवेगावर परिणाम होऊन दाबाचे प्रमाण वाढते व दाबाची प्रचंड लाट निर्माण होते आणि प्रतिस्रोत भागात कोटरीभवन झाल्याने जलाघात निर्माण होतो. जलाघातामुळे नळ फुटण्याचा धोका असतो.

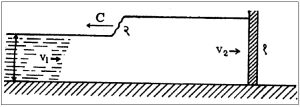
ऊर्मी : कालव्यातून v₁ वेगाने वाहणारा प्रवाह अचानकपणे बंद केला किंवा कमी केला, तर अनुस्रोत भागांत किंवा प्रतिस्रोत भागांत वेग कमी (v₂) होऊन ऊर्मी तरंग निर्माण होतात (आ. २४).

द्रायुमापन : द्रायूंचे प्रवाहमान व आकारमान (घनफळ) मोजण्याकरिता विविध प्रकारचे द्रायुमापक वापरतात [→ द्रायुमापक].

दाबमापन : नळ, नलिका यांमधून वाहणाऱ्या द्रव पदार्थांचा दाब, वातावरणीय दाब इ. द्रायूंचे दाब मोजण्यासाठी दाबाच्या निरनिराळ्या मर्यादांकरिता विविध प्रकारचे दाबमापक उपलब्ध आहेत [→ दाब व दाबमापन ].

पहा : ऊष्मागतिकी; द्रविकी; द्रायुमापक; वायुयामिकी; स्थिति समीकरण.

संदर्भ : 1. Binder, R. C. Fluid Mechanics, Englewood Cliffs, N. J., 1966.

2. Daily, J. W.; Harleman, D. R. T. Fluid Dynamics, Reading, Mass., 1966.

3. Duncan, W. J.; Thom, A. S.; Young, A. D. An Elementary Treatise on the Mechanics of Fluids, London, 1960.

4. Hansen, A. G. Fluid Mechanics, New York, 1967.

5. Kaufman, W. Fluid Mechanics, New York, 1963.

6. Longwell, P. A. Mechanics of Fluid Flow, New York, 1966.

7. Robinson, J. L. Basic Fluid Mechanics, New York, 1963.

8. Rouse, H. Fluid Mechanics for Hydraulic Engineers, New York, 1961.

9. Streeter, V. L., Ed. Handbook of Fluid Dynamics, New York, 1961.

10. Streeter, V. L. Fluid Mechanics, New York, 1966.

11. Vennard, J. K. Elementary Fluid Mechanics, New York, 1961.

पुरोहित, वा. ल.; घुणकीकर, ज. तु.; दांडेकर, मो. मा.