चलनकलन

चलनकलन : ही ⇨ कलनशास्त्राची एक उपशाखा होय. एखाद्या दिलेल्या फलनाची (गणितीय संबंध दर्शविणाऱ्या राशीची) लघुत्तम किंवा महत्तम मूल्ये शोधून काढणे हा अवकलनाच्या [⟶अवकलन व समाकलन] साहाय्याने सोडवता येणाऱ्या अनेक प्रश्नांपैकी एक प्रश्न आहे.

मूलभूत सिद्धांत : चलनकलनामध्ये एखादा दिलेला समाकल लघुत्तम वा महत्तम होईल असे फलन शोधून काढणे याचा विचार होतो. पर्यायाने त्या समाकलावर अवलंबून असणाऱ्या गोष्टींच्या लघुतम व महत्तम मूल्यांचाही अभ्यास करता येतो. उदा., पुढील प्रश्न विचारात घेऊ.

क्ष आणि य या दोन चलांमधील असा अन्योन्य फलनसंबंध शोधू काढावयाचा आहे की,

हा समाकल लघुत्तम किंवा महत्तम मूल्य धारण करील. यामध्ये य’= ^{d य} /_{d क्ष} असून अ, आ अचल आहेत. तसेच फ हे फलन दिलेले असून, (अ, आ) अंतरालात फ चे क्ष, य, य’ सापेक्ष आंशिक अवकलज चतुर्थ कोटीपर्यंत तरी अस्तित्वात आहेत. भूमितीय दृष्टिकोनातून हाच प्रश्न पुढे दिल्याप्रमाणे मांडता येईल. क्ष, य आलेखपटावर दोन स्थिर बिंदू (ज्यांचे क्ष सहनिर्देशक म्हणजे स्थाननिर्देशक आकडे अ आणि आ आहेत) दिले आहेत. हे दोन बिंदू जोडणारे अनेक वक्र असू शकतात आणि अशा प्रत्येक वक्रास अनुसरून वर दिलेला समाकल काढता येतो. तर या सर्वांमधून असा वक्र शोधून काढावयाचा आहे की, त्याला अनुसरून वर दिलेला समाकल घेतल्यास त्याचे मूल्य लघुतम वा महत्तम असेल. अशा वक्रास ग्राह्य वक्र म्हणतात.

समजा, य = प (क्ष) हे ग्राह्य वक्राचे समीकरण आहे. अर्थातच हा वक्र क [अ, प (अ)] आणि ख [आ, प (आ)] या दिलेल्या दोन बिंदूंतून जातो. आता या दिलेल्या दोन बिंदूंतून जाणाऱ्या इतर वक्रांपैकी, ग्राह्य वक्राला अगदी लगतचा असा वक्र य = प (क्ष) + त भ (क्ष) या समीकरणाने दर्शवू. यामध्ये त हे अचल पद असून ते क्ष, य वर अवलंबून नाही. तसेच भ (क्ष) हे फलन त विरहित आहे. समजा, य अक्षास समांतर अशी रेषा या दोन वक्रांस अनुक्रमे म आणि ग या बिंदूंमध्ये छेदते. आ.१ मध्ये कमख हा ग्राह्य वक्र असून त्यालगतचा वक्र कगख असा दाखवला आहे. तसेच हा लगतचा वक्रही क, ख या बिंदूंतून जात असल्याने भ (अ) = भ (आ) = ० असलेच पाहिजे हे उघड आहे. आ.१ वरून म चा (आणि ग चा) क्ष – सहनिर्देशक जर क्ष असेल तर, मग = त भ (क्ष) असले पाहिजे, हे सहज लक्षात येईल. तसेच लगतच्या वक्राकरिता य’ = प’ (क्ष) + त भ’ (क्ष) असेल. आता त ⟶ ० असेल, तर बिंदू ग ⟶  बिंदू म आणि लगत वक्राला ग शी असलेल्या स्पर्शिकेचा उतार ⟶ ग्राह्य वक्राला म शी असलेल्या स्पर्शिकेचा उतार, हे उघड आहे.

समजा, दिलेल्या समाकल स चे, ग्राह्य वक्राला अनुसरून काढलेले  मूल्य स_म असे लिहिले आणि लगत वक्राला अनुसरून जे मूल्य मिळेल  त्या स_ग असे म्हटले, तर

टेलर विस्तार वापरल्यास [⟶ अवकलन व समाकलन],

फ (क्ष, प + त भ, प’ + त भ’) = फ (क्ष, प, प’)

असे लिहिता येईल. त्यावरून खालील समीकरण मिळेल.

आता कमख हा ग्राह्य चक्र असल्यास, स_म हे स चे लघुत्तम व महत्तम मूल्य असले पाहिजे. यांचा वेगवेगळा विचार करू.

(१) समजा, स_म हे लघुत्तम मूल्य आहे तर इतर कोणत्याही वक्रासाठी (म्हणजेच त च्या कोणत्याही अत्यल्प मूल्यासाठी) स_ग &gt स_म असले पाहिजे. हे

असेल तरच शक्य होईल.

(२) समजा, स_म हे महत्तम मूल्य आहे तर वरीलप्रमाणेच विचार करून

असले पाहिजे.

वरील दोन्हींचा एकत्रित विचार करता, य = प (क्ष) हा ग्राह्य वक्र असण्याची अट म्हणजेच

आता भागशः समाकलचाच्या सूत्राने

यावरून समाकल लघुतम वा महत्तम असण्याची अट

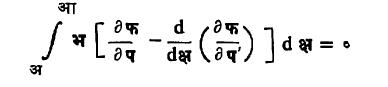
अशी लिहिता येते, पण भ (क्ष) हे फलन कसल्याही प्रकारचे असू शकेल. कोणत्याही भ साठी वरील अट पूर्ण व्हावयास हवी असेल तर

म्हणजेच, वरील समीकरण (यास ऑयलर यांचे समीकरण म्हणतात), हे पाहिजे असलेल्या अटीचे स्वरूप होय. यामध्ये, दिलेल्या फ वरून

काढून त्याची मूल्य घातल्यास क्ष, य मधील अवकल समीकरण मिळेल. त्याचा निर्वाह (उत्तर) म्हणजेच आपल्यास पाहिजे असलेल्या ग्राह्य वक्राचे समीकरण होय.

उपयोग : वर दिलेल्या सिद्धांताचा उपयोग पुढे दिलेल्या (ऐतिहासिक महत्त्वाच्या) उदाहरणांनी अधिक स्पष्ट होईल.

(१) प्रतलावरील दिलेल्या दोन बिंदूंना जोडणारा लघुतम लांबीचामार्ग शोधणे : त्या बिंदूंना जोडणारी सरळ रेषा हाच लघुतम लांबीचा मार्ग आहे हे सर्वश्रुत आहे. वर दिलेल्या सूत्राचा उपयोग याबाबतीत कसा होतो हे येथे दर्शविले आहे. समजा, क्षय प्रतलावर क, ख असे दोन बिंदू (क्ष-सहनिर्देशक अनुक्रमे अ, आ) घेतले. त्यांना जोडणाऱ्या वक्राची, क ते ख ही लांबी स असेल तर

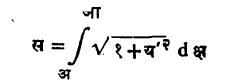
हे कलनशास्त्रातील सूत्र आहे. आता ऑयलर समीकरणातील फ म्हणजे

 .^..य = उ क्ष + इ असे एकघाती समीकरण मिळते. यावरून पाहिजे असलेला ग्राह्य वक्र ही क, ख ला जोडणारी सरळ रेषा होय.

एखाद्या वक्रपृष्ठावर दोन बिंदू घेऊन, ते पृष्ठ न सोडता आणि त्या बिंदूंना जोडणारा असा लघुतम लांबीचा मार्ग शोधता येईल. अशा प्रश्नांच्या अभ्यासामुळे अल्पिष्ठ (अल्पांतरीय) रेषांच्या अभ्यासास चालना मिळाली.

(२) समजा, एका क्षितिजलंब प्रतलात दोन बिंदू दिले आहेत. मात्र ते एकाच उभ्या रेषेत किंवा एकाच आडव्या रेषेत नाहीत. त्यांना जोडणाऱ्या वक्रावरून घर्षणविरहित रितीने एक वस्तुकण फक्त गुरुत्वाकर्षणाच्या प्रभावाखाली घसरत आहे. जर तो कण वरच्या बिंदूपासून खालच्या बिंदूपर्यत लघुतम वेळात यावयाचा असेल तर त्या वक्राचा आकार कसा असावा ? म्हणजेच त्या वक्राचे समीकरण काय असावे ?

वरील बिंदू अ आदिबिंदू घेऊन आणि य अक्ष अधोमुख घेऊन य अंतर आल्यावर कणाचा वेग

असणार (ग – गुरुत्वाकर्षणाचा स्थिरांक). अ पासून आ पर्यंतचे वक्रावरील अंतर आक्रमावयास लागणारा काल स असेल तर,

 असे मिळते (ख – स्थिरांक कोस्प, कोज्या, स्प ही त्रिकोणमितीय गुणोत्तरे आहेत). क्ष, य ची मूल्ये ψ मध्ये देणारी वरील दोन समीकरणे म्हणजे चक्रज या वक्राची प्रचलीय समीकरणेच होत. चक्रज हा, वर्तुळ एका 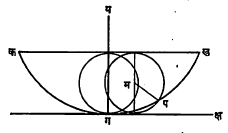रेषेवर फिरत असताना वर्तुळावरील स्थिर बिंदूने रेखाटलेला आलेख होय. उदा., वाहन रस्त्यावरून जात असताना त्याच्या चाकाच्या परिघावरील बिंदू चक्रज रेखाटील. आ. २ मध्ये म मध्य असलेले वर्तुळ कख या रेषेवर फिरत असून त्या वर्तुळावरील प बिंदूचा आलेख (कगपख ने दर्शविलेला) चक्रज आहे. ग या बिंदूला चक्रजाचा शिरोबिंदू म्हणतात. यावरून चक्रज हा हवा असलेला ग्राह्य वक्र होय. याला लघुत्तम काल वक्र (ब्राकिस्तोक्रोन) असे नाव दिले आहे.

हा प्रश्न झां बेर्नुली (१६६७-१७४८) ह्या स्वीस गणितज्ञांनी इतरांना, विशेषतः न्यूटन यांना आव्हान म्हणून टाकला होता (न्यूटन यांनी तो एक दिवसात सोडवला). लायप्निट्‌स, लॉपीताल, झांक बेर्नुली आणि स्वतः झां बेर्नुली यांनीही स्वतंत्रपणे सोडवला.

(३) समपरिमितीय प्रश्न : दिलेली परिमिती असलेला व लघुतम क्षेत्र परिवेष्टित करील असा वक्र शोधणे, अशा प्रकारच्या प्रश्नास समपरिमितीय प्रश्न म्हणतात. वर वर्णिलेल्या रीतीने या प्रश्नाचे उत्तर म्हणजे दिलेल्या लांबीचा परिघ असलेले वर्तुळ हे सिद्ध करता येते.

तसेच दिलेले पृष्ठफळ असलेला आणि महत्तम अवकाश परिवेष्टित करील असा पृष्ठ म्हणजे गोल होय हे सिद्ध करता येते.

(४) समजा, एक रेषा आणि तिच्या एकाच बाजूस पण तिला लंब असणाऱ्या रेषेवर नसलेले दोन बिंदू घेतले. ते त्या रेषेला न छेदणाऱ्या एका वक्राने जोडले आणि अशी एक प्रतलीय आकृती त्या रेषेभोवती फिरविली. अशा पद्धतीने मिळणाऱ्या भ्रमणपृष्ठाचे क्षेत्रफळ लघुतम असण्यास तो वक्र कोणता असावा ? ह्या प्रश्नाचे उत्तरही वर दिलेल्या पद्धतीने मिळते. सर्वत्र सारखी असलेली वजनदार दोरी, दिलेल्या बिंदूंना बांधून लोंबती ठेवली असता जो आकार मिळतो त्याला रज्जुवक्र (कॅटेनरी) म्हणतात. हाच या उदाहरणातील ग्राह्य वक्र होय.

इतिहास : अशा प्रकारच्या प्रश्नांच्या अभ्यास ऑयलर यांनी बेर्नुली यांच्या सांगण्यावरून सुरू केला असता त्यांना चलनकलनाचा शोध लागला. परंतु इटलीत जन्मलेले फ्रेंच गणितज्ञ लाग्रांझ यांनी वयाच्या अवघ्या एकोणिसाव्या वर्षी समपरिमितीय प्रश्नांचे उत्तर शोधून काढले व ते ऑयलर यांना पाठविले. ऑयलर यांनी ह्या तरुण गणितज्ञाला प्रसिद्ध केले. लाग्रांझ यांनी केवळ हा प्रश्नच सोडवला असे नव्हे तर नवीन पद्धती शोधून काढल्या. त्या पूर्वीच्या पद्धतींपेक्षा अधिक व्यापक होत्या. अशा रीतीने चलनकलनाचा शोध लागला.

हॅमिल्टन यांचे किमान कार्य – तत्त्व : गतिकीमध्ये (गती आणि तिचा प्रेरणेशी असणारा संबंध यांचा अभ्यास करणाऱ्या शास्त्रात) गतिज ऊर्जा उणे स्थितिज ऊर्जा यास लाग्रांझीय म्हणतात. ते ल ने दर्शविल्यास लाग्रांझ यांची जी गतिसमीकरणे येतात ती वर चर्चिलेल्या ऑयलर समीकरणासारखीच असतात (फक्त क्ष ऐवजी कालनिदर्शक ट हे निरवलंबी चलपद असते). लघुतम मूल्यी होतो आणि अ ते आ हा वस्तुकणाचा मार्ग म्हणजे या अटीमुळे मिळालेला ग्राह्य वक्र असतो. याचाच अर्थ असा की, प्रत्येक वस्तुकणाचा गतिमार्ग हा ग्राह्य वक्र असतो.

यावरून गतिमान वस्तुकणाचा मार्ग निश्चित करावयाचा झाल्यास वरील समाकल लघुतम होईल असे गणित कृत्य करावयाचे, हे तत्त्व हॅमिल्टन या आयरिश गणितज्ञांनी प्रथम मांडले. यासच हॅमिल्टन यांचे किमान कार्य-तत्त्व असे म्हणतात.

गतिकी, ज्योतिषशास्त्र व गणितीय भौतिक यांत अंतर्भूत वस्तुकणांचे मार्ग याच तत्त्वाचा अवलंब करीत असल्याने चलनकलनशास्त्राच्या अभ्यासास विशेष चालना मिळाली आहे. आइन्स्टाइन यांचा ⇨सापेक्षता सिद्धांत  व श्रोडिंजर यांचा पुंज सिद्धांत [→ पुंजयामिकी] या दोन्हींमध्ये चलनकलनशास्त्राचा सिद्धांत महत्त्वपूर्ण गणला जातो.

संदर्भ : 1. Bliss, G. A. Lectures on the Calculus of Variations, Chicago, 1946.

           2. Weinstock, R. Calculus of Variations, with Applications to Physics and Engineering, New York, 1952.

गुर्जर, ल. वा.

“