किरणोत्सर्ग : काही विशिष्ट मूलद्रव्यांच्या अणुगर्भांच्या (अणुकेंद्रांच्या) अस्थिरतेमुळे स्वयंप्रेरित विघटन (फुटण्याची क्रिया) होते आणि त्यामुळे काही किरणांचे वा कणांचे उत्सर्जन होते, या आविष्काराला किरणोत्सर्ग म्हणतात. राँटगेन यांच्या क्ष-किरणांच्या शोधानंतर (१८९५) थोड्याच महिन्यांत १८९६ मध्ये आंत्वान आंरी बेक्रेल यांना किरणोत्सर्गाचा शोध आकस्मिकपणे लागला. अनुस्फुरण (एखाद्या पदार्थाने एखाद्या विशिष्ट तरंगलांबीच्या प्रारणाचे म्हणजे तरंगरूपी ऊर्जेचे शोषण करून जास्त तरंगलांबीच्या प्रारणाचे उत्सर्जन करणे) या आविष्काराबद्दल संशोधन करीत असताना बंद पाकिटात ठेवलेल्या छायाचित्रण काचा व बोहीमियामधील पिचब्लेंड या युरेनियम ऑक्साइडयुक्त खनिजाचा संबंध आला होता या काचा धुतल्या असता त्या काळ्या झालेल्या बेक्रेल यांना आढळून आल्या, साहजिकच या पिचब्लेंडमध्ये असलेल्या युरेनियमाच्या पारगामी (आरपार जाणाऱ्या) किरणांमुळे असे झाले असले पाहिजे असा बेक्रेल यांनी तर्क केला व या प्रकारास त्यांनी किरणोत्सर्ग हे नाव दिले. सुरुवातीच्या संशोधनावरून या किरणोत्सर्गाचे मूळ अणुगर्भाशी निगडित असून या आविष्कारावर रासायनिक विक्रियांचा तसेच भौतिकीय परिस्थितीचा काहीही परिणाम होत नाही असे आढळले.
सॉरबॉन येथील विद्यार्थी प्येअर क्यूरी व मारी क्यूरी यांनी किरणोत्सर्गाचे कारण शोधून काढण्याचे काम अंगावर घेतेले व त्याचे पर्यवसान म्हणून प्रथम पोलोनियम आणि नंतर रेडियम या किरणोत्सर्गी मूलद्रव्यांचा शोध लागला.
किरणोत्सर्गाच्या क्रियेमध्ये अणुगर्भाचे विघटन होऊन त्याचे दुसऱ्या प्रकारच्या अणुगर्भात रूपांतर होत असते असे रदरफर्ड आणि सॉडी या शास्त्रज्ञांनी दाखवून दिले. अणूचे अस्थैर्य हे किरणोत्सर्गाचे कारण असते आणि असे अस्थिर अणू निसर्गात सर्वसाधारणपणे अणुक्रमांक (अणुगर्भातील प्रोटॉनांची संख्या) ८२ ते ९२ पर्यंत आढळतात. रदरफर्ड यांचा दुसरा शोध म्हणजे अणुगर्भाचा. अणूचा प्रकार आणि त्याचे रासायनिक गुण हे अणुगर्भावरच अवलंबून असतात. रदरफर्ड यांचा तिसरा एतद्विषयक शोध म्हणजे उत्सर्जित किरण तीन प्रकारचे असतात हा होय. हे तीन प्रकार म्हणजे (१) आल्फा (α) किरण : हे हीलियम या मूलद्रव्याचे अणुगर्भ होत, (२) बीटा (β) किरण : हे इलेक्ट्रॉनच होत आणि (३) गॅमा (γ) किरण : म्हणजे विद्युत् चुंबकीय प्रारणाचे पुंज (विभाजन करता येत नाही अशी किमान राशी, क्वांटम) होत. १९१९ मध्ये कमी अणुक्रमांकाच्या अणुगर्भावर α कणांनी आघात केल्यास त्याचे विघटन होऊन रूपांतरण (एका मूलद्रव्यापासून दुसरे मूलद्रव्य तयार होणे) होते आणि त्यातून प्रोटॉन (p) बाहेर पडतात असे रदरफर्ड यांनी सिद्ध केले. या पहिल्या कृत्रिम विघटन क्रिया होत. १९३४ मध्ये ईरेन झॉल्यो-क्यूरी आणि जे. एफ्. झॉल्यो या दांपत्याने ॲल्युमिनियमावर α कणांचा आघात करून त्यातून पॉझिट्रॉन (इलेक्ट्रॉनाइतकेच द्रव्यमान व विद्युत् भार असलेले पण विद्युत् भार धन असलेले मूलकण) बाहेर पडतात असा शोध लावला. विघटित केंद्रांचे रूपांतर किरणोत्सर्गी फॉस्फरसामध्ये होते व या फॉस्फरसाच्या अणुगर्भातून पॉझिट्रॉन उत्सर्जित होतात असे दिसून आले. या घटनेला त्यांनी प्रवर्तित किरणोत्सर्ग असे नाव दिले.
आता प्रयोगशाळेमध्ये कणांच्या भडिमाराने बहुतेक सर्व मूलद्रव्ये किरणोत्सर्गी करता येतात आणि विविध समस्थानिक (अणुक्रमांक तोच पण अणुभार भिन्न असलेले त्याच मूलद्रव्याचे प्रकार) उपलब्ध झाल्याने त्यांचा भौतिकी, रसायनशास्त्र, प्राणिविज्ञान, वनस्पतिविज्ञान, वैद्यकशास्त्र इ. अनेक शास्त्रांतील प्रश्न सोडविण्याकरिता उपयोग होतो [→ अणुऊर्जेचे शांततामय उपयोग समस्थानिक].
कोणत्याही किरणोत्सर्गी मूलद्रव्यातून अणूच्या प्रकाराप्रमाणे α किंवा β आणि काही वेळा γ किरण उत्सर्जित होतात. परंतू एकाच अणूमधून एकाचवेळी α आणि β असे दोन्ही प्रकारचे किरण उत्सर्जित होत नाहीत. मूलद्रव्याची किरणोत्सर्गी कार्यप्रवणता (प्रतिसेकंदास विघटित होणाऱ्या अणूंची संख्या) कालौघाप्रमाणे घटत असते. ही कार्यप्रवणता, अस्तित्वात असलेली किरणोत्सर्गी अणुसंख्या आणि तद्विशिष्ट क्षयांक (λ, याची व्याख्या खाली दिली आहे) यांवर अवलंबून असते. द्रव्यविशिष्ट कार्यप्रवणता एका ठराविक कालात अर्धी होते. या कालास त्या मूलद्रव्याचे अर्धायुष्य (T) किंवा कार्यप्रवणता निम्मी होण्याचा काल म्हणतात. रेडियमाचे अर्धायुष्य १,६२० वर्ष आहे. या अवधीत मूळच्या एक ग्रॅम रेडियमपैकी ०⋅५ ग्रॅम रूपांतरित होऊन जाईल.
किरणोत्सर्गाचे प्रकार : किरणोत्सर्गी पदार्थातून निघणाऱ्या किरणांचे α, β, γ हे प्रकार असून, किरणोत्सर्गी विघटन क्रियांमध्ये समघटकीय संक्रमण [एका अणुगर्भीय समघटकाचे (एकच अणुक्रमांक व तोच द्रव्यमानांक, म्हणजे अणुगर्भातील प्रोटॉन व न्यूट्रॉन यांची एकूण संख्या, असलेल्या परंतु मोजण्याइतक्या कालावधीकरिता ऊर्जेच्या निरनिराळ्या अवस्थांत असलेल्या दोन किंवा अधिक अणूंपैकी एकाचे) त्याच्यापेक्षा कमी ऊर्जेच्या दुसऱ्या समघटकात होणारे किरणोत्सर्गी संक्रमण ] आणि इलेक्ट्रॉन-ग्रास यांचाही समावेश होतो. पण द्विभंजन (अणुगर्भाचे दोन तुकडे होणे) ही एक खास प्रकारची अणुगर्भीय विक्रिया असून तिचा या प्रकारात समावेश करता येत नाही. या सर्व प्रकारांत उत्सर्जित होणारे कण, अणुक्रमांकांतील बदल आणि द्रव्यमानांकांतील बदल सोदाहरण खालील कोष्टकांत दर्शविले आहेत.
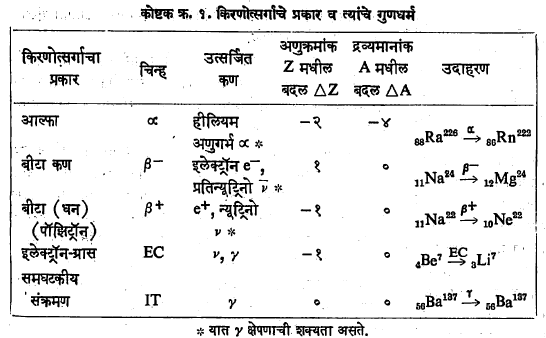
जनक अणुगर्भातून उत्सर्जन झाल्यावर राहिलेल्या अणूस अपत्य अणू म्हणतात. याचा अणुक्रमांक आणि द्रव्यमानांक सॉडी यांच्या स्थलांतर नियमाप्रमाणे निश्चित होतो हे कोष्टकावरून दिसून येईल.
किरणोत्सर्गी क्षयांक : कार्यप्रवणता : किरणोत्सर्गी मूलद्रव्याच्या अणूंची संख्या कालगतीने घटत असते. प्रत्येक सेकंदाला एखाद्या अणूची अपत्य अणूमध्ये रूपांतर होण्याची संभाव्यता ही एक निश्चित अपूर्णांक असते, त्याला क्षयांक म्हणतात. एकानंतर दुसरा कोणता अणू व केव्हा विघटित होणार हे काही सांगता येणार नाही. परंतु एखाद्या पदार्थातील अणूंची संख्या मोठी असल्यास त्या अणूंपैकी प्रतिसेकंदास कितींचा ऱ्हास किंवा क्षय होईल हे निश्चित सांगता येते. याप्रमाणे प्रतिसेकंदास अणुविघटनाची सांख्यिकीय (संख्याशास्त्रीय) संभाव्यता किंवा क्षयांक (λ) याची व्याख्या पुढील समीकरणाने दिली जाते.
| λ= – | 1 | . | dA |
| A | dt |
एखाद्या पदार्थातील प्रतिसेकंदास विघटित होणाऱ्या अणुसंख्येस पदार्थाची किरणोत्सर्गी कार्यप्रवणता म्हणतात. म्हणून
| Aλ= – | dA | … …. (१) |
| dt |
येथे A ही अणूंची संख्या आहे.
क्षयांक λ हा त्या मूलद्रव्याचा विशिष्ट असा अंक असतो. त्यामुळे निश्चित झाला की, त्या किरणोत्सर्गी पदार्थाची जात (म्हणजे ते मूलद्रव्य) निश्चित होते. नैसर्गिक व कृत्रिम मिळून सु. १,००० प्रकारचे किरणोत्सर्गी अणुगर्भ ज्ञात झाले आहेत. क्षयांक λ पदार्थाच्या रासायनिक संयोगावस्था, तपमान, दाब, वय वगैरे भौतिक परिस्थितींवर अवलंबून नसतो. क्षयांकाचा पल्ला ३ x १०६ प्रतिसेकंदापासून २⋅६ x १०-१८ प्रतिसेकंदापर्यंत आढळला आहे.
दुहेरी व तिहेरी किंवा वैकल्पिक ऱ्हासाचे प्रकार : बऱ्याच किरणोत्सर्गी पदार्थांतून दोन किंवा अधिक प्रकारचे किरण बाहेर पडतात. युरेनियम (२३८) चा ऱ्हास α कणाच्या उत्सर्जनाने वा आकस्मिक स्वयंस्फूर्त द्विभंजन विक्रियेनेही होतो. तांबे तीन प्रकारांनी क्षय पावते. (१) ऋण बीटा उत्सर्जन, (२) घन बीटा उत्सर्जन व (३) इलेक्ट्रॉन – ग्रास (इ. ग्रा.). ज्यावेळी एकाच प्रकारच्या अणुगर्भांतून दोन स्वतंत्र तऱ्हेने किरणांचे दोन प्रकार उत्सर्जित होतात तेव्हा त्यास दुहेरी शाखात्मक किरणोत्सर्ग म्हणतात.
वैकल्पिक क्षयाच्या प्रकारामध्ये प्रत्येक शाखेसाठी λ चे वेगवेगळे मूल्य असते. जसे λ1, λ2, λ3… वगैरे. प्रतिसेकंदास क्षयाची संपूर्ण सांख्यिकीय संभाव्यता λ आणि पूर्वोक्त शाखा-क्षयांक हे संभाव्यतेच्या नियमाप्रमाणे संबंधित असतात. निरनिराळे शाखा – क्षयांक स्वतंत्र असल्यामुळे संपूर्ण संभाव्यता त्या सर्वांच्या बेरजेबरोबर असते.
λ = λ1 + λ2 + λ3 … …. ….. (२)
संबंधित मूलद्रव्याचे सर्व अणू A असतील तर विविध किरणोत्सर्गी कार्यप्रवणता प्रत्येकी Aλ1, Aλ2, Aλ3….अशा असतील आणि संपूर्ण कार्यप्रवणता Aλ याचे सूत्र
Aλ = Aλ1 + Aλ2 + Aλ3 + … …. ….. (३)
असे मिळेल.
विविध शाखांची कार्यप्रवणता [उदा., तांबे (६४) च्या बाबतीत β–, β+ आणि इ. ग्रा.] संपूर्ण कार्यप्रवणतेच्या ठराविक प्रमाणांत असते.
| Aλ1 | = | λ1 | Aλ2 | = | λ2 | … … … वगैरे | ||
| Aλ | λ | Aλ | λ |
या प्रमाणास शाखा – गुणोत्तर म्हणतात. उदा., तांबे (६४) च्या बाबतीत
λβ-/λ = ०⋅४०; λβ-/λ = ०⋅२० आणि λEC / λ = ०⋅४० सर्व गुणोत्तरांची बेरीज नेहमी एक असते.
द्वि-बीटा किरणोत्सर्ग : सैद्धांतिक दृष्ट्या एकच द्रव्यमानांक असणाऱ्या समप्रोटॉन-समन्यूट्रॉन असलेल्या दोन स्थायी अणुगर्भांमधील संक्रमण द्वि-बीटा उत्सर्गाने शक्य आहे असे एक उदाहरण

किरणोत्सर्गी क्षयाचा नियम : एखाद्या किरणोत्सर्गी मूलद्रव्याचे सुरुवातीला A0 अणू असतील तर ही संख्या कालगतीप्रमाणे घटत जाईल. किरणोत्सर्गी कार्यप्रवणतेचे सूत्र लक्षात घेता कोणत्याही क्षणी

अर्धायुष्य आणि माध्य आयुष्य : अर्धायुष्य T म्हणजे कोणत्याही किरणोत्सर्गी अणूचा ज्या कालावधीत क्षय न होण्याची संभाव्यता ½ असते तो काल. समी. (४) वरून
| T = | Loge2 | = | 0⋅693 | …. …… (५) |
| λ | λ |
असे मिळते. मूळ अणुसंख्या Ao मोठी असल्यास T या कालानंतर Aλ ही A०λ च्या बरोबर निम्मी होईल. अणुसंख्या A = Ao/2 झालेली असेल. म्हणून अर्धायुष्य हे अर्ध्या पदार्थाचे आयुष्य असे म्हणावयास हरकत नाही.
माध्य आयुष्य : कोणत्याही एका अणूचे आयुष्य ० ते ∞ च्या दरम्यान काहीही असू शकेल. सांख्यिकीच्या दृष्टीने अणूंची संख्या पुरेशी मोठी असेल तरच अणूंचे माध्य (सरासरी) आयुष्य याला काही अर्थ आहे. विशिष्ट मूलद्रव्याच्या माध्य आयुष्याचे मूल्य हे निश्चित असते. सुरुवातीस Ao अणू असल्यास t कालानंतर A = Aoe-λt इतके अणू असतील. या प्रत्येक अणूचे आयुष्य t पेक्षा अधिक असेल. यांपैकी जे dt या आणखी कालावधीत क्षय पावतील त्यांचे आयुष्य प्रत्येकी t धरता येईल. म्हणून Aλ dt इतक्या अणूंचे आयुष्य प्रत्येकी t असेल. सर्व अणूंचे एकूण आयुर्मान L म्हणजे या सर्वांची बेरीज
![]()
म्हणून माध्य आयुष्य किंवा प्रत्येक अणूची आयुर्मान अपेक्षा L/A किंवा 1/λ असेल.
माध्य आयुष्य T = 1/λ …. …. …. (६)
समी. (४) मध्ये t चे मूल्य T घातल्यास, अणुसंख्या किंवा कार्यप्रवणता मूळ किंमतीच्या e-1 इतकी पट म्हणजे ०⋅३६८ इतकी पट झालेली आढळेल. म्हणून माध्य आयुष्य हा काल विशिष्ट किरणोत्सर्गी अणूंची संख्या मूळ संख्येच्या e-1 पट होण्यास लागणारा काल होय.
माध्य आयुष्य आणि अर्धायुष्य यांचा संबंध समी. (५) व (६) वरून स्पष्ट होतो.
| T = | T | = 1.44 T | = | 1 | …. ….. (७) |
| 0⋅693 | λ |
अर्धायुष्य T याचा उपयोग नेहमी व्यवहारात अधिक करतात.
किरणोत्सर्गी श्रेणी आणि त्यातील मूलद्रव्यांचा क्षय : नैसर्गिक किरणोत्सर्गी मूलद्रव्यांच्या श्रेणी झालेल्या आढळतात म्हणजे एका जनक अणूचा अपत्य अणू, पुन्हा त्याचा अपत्य अणु वगैरे अशी शेवटच्या स्थिर अणूपर्यंत एक वंशावळच निर्माण होते. अशाच प्रकारच्या श्रेणी कृत्रिम किरणोत्सर्गी मूलद्रव्यांच्या बाबतीतही आढळल्या आहेत. समजा, श्रेणीची सुरुवात A या मूलद्रव्याने झाली आणि त्यापासून अनुक्रमे B, C, D वगैरे अपत्य मूलद्रव्ये उत्पन्न झाली. ही श्रेणी पुढीलप्रमाणे दिसेल :

हे त्या त्या मूलद्रव्यांच्या अणूंची संख्या व λA, λB, λC,… हे त्या त्या मूलद्रव्यांचे क्षयांक होत. समजा, प्रथम (t = 0), A = A0 व B = C = D = 0, तर कोणत्याही t या काली असणाऱ्या B, C, D वगैरे अणूंची संख्या पुढे दिलेल्या सूत्राप्रमाणे येते [याचे गणित मूलभूत समी. (४) यावर अवलंबून आहे].

निरनिराळ्या मूलद्रव्यांची किरणोत्सर्गी कार्यप्रवणता AλA, BλB, CλC, DλD अशी असेल. गणिताच्या सौकर्यासाठी
| λ1 | = | T2 | |
| λ1– λ2 | T2 – T1 |
अशी सूत्रे वापरणे अधिक व्यवहार्य आहे.पुष्कळदा अपत्य मूद्रव्याची कार्यप्रवणता आणि शिल्लक राहिलेली जनक मूलद्रव्याची कार्यप्रवणता यांचे प्रमाण आपणास पाहिजे असते. उदा.,

आणि जनक मूलद्रव्य A चे अर्धायुष्य हे अपत्य मूलद्रव्य B आणि C या दोहोंच्या अर्धायुष्यांपेक्षा जास्त असेल, तर TB आणि TC यापेक्षा बऱ्याच मोठ्या कालाकरिता
| CλC | = | TA | . | TA | … … (११) |
| AλA | TA – TB | TA – TC |
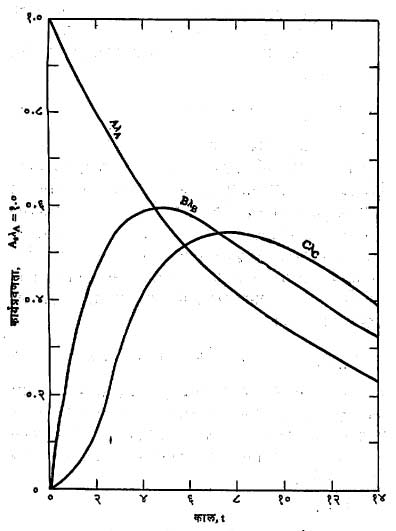
आ. १ मध्ये किरणोत्सर्गी श्रेणीतील A चा क्षय आणि B व C यांची वृद्धी व क्षय दाखविली आहेत.
किरणोत्सर्गी समतोल : किरणोत्सर्गी श्रेणींचे गणित खालील मूलभूत समीकरणाधिष्ठित आहे.
| dB | = | AλA – BλB | …. …. ….. (१२) |
| dt |
| येथे | dB | म्हणजे |
| dt |
अणूंच्या वृद्धीचा वेग, AλAजनक A ची कार्यप्रवणता = जनक अणूंच्या क्षयाचा वेग, आणि BλB = अपत्य अणूच्या क्षयाचा वेग. ज्यावेळी
| dB | = 0 |
| dt |
असेल तेव्हा B च्या अणूंची संख्या वाढतही नाही व कमीही होत नाही. हाच किरणोत्सर्गी समतोल होय. परंतु हा समतोल क्षणिकच असू शकेल. हा क्षण म्हणजे BλB चे मूल्य कमाल असण्याचा क्षण होय (आ. १). या क्षणाचे मूल्य tm गणिताने येते ते असे :
![]()
या क्षणी AλA = BλB … … … (१४)
अशा अवस्थेला आदर्श समतोल म्हणतात. tm या क्षणापूर्वी जनक मूलद्रव्याची कार्यप्रवणता अपत्य मूलद्रव्याच्या कार्यप्रवणतेपेक्षा अधिक असते व नंतर कमी होते.
किरणोत्सर्गी जनक मूलद्रव्याचे अर्धायुष्य अपत्य मूलद्रव्यापेक्षा अधिक असेल तर प्रथमत:
| BλB | |
| AλA |
हे गुणोत्तर वाढत जाते व नंतर त्याचे मूल्य स्थिर होते. t हा काल
| TB . TA | |
| TA – TB |
च्या मानाने फार मोठा असेल, तर
| BλB | = | TA | = स्थिरांक … ….. (१५) |
| AλA | TA – TB |

होईल. अशा समतोलास दीर्घकालीक समतोल हे नाव आहे. याचे उत्तम उदाहरण युरेनियम-रेडियम (T = १,६२० वर्षे) किंवा रेडियम-रेडॉन (T = ३⋅८२५ दिवस) यांच्या समतोलाचे आहे. दीर्घकालीक समतोलाच्या कालावधीत जनक मूलद्रव्याच्या अणुसंख्येत म्हणण्यासारखा फरक पडत नाही.
नैसर्गिक किरणोत्सर्ग : साधारणत: निसर्गामध्ये ८२ ते ९२ अणुक्रमांकाची मूलद्रव्ये स्वयंस्फूर्त किरणोत्सर्ग करताना आढळतात. याला नैसर्गिक किरणोत्सर्ग म्हणतात. भूविज्ञानाप्रमाणे पृथ्वीचे वय सु. ३ ते ५ x १०९ वर्षे मानले जाते. पृथ्वीच्या जन्मापासूनच वरीलपैकी काही किरणोत्सर्गी मूलद्रव्ये उपस्थित असतील, तर त्यांचे अर्धायुष्य वरील आकड्याच्या जवळपास असले पाहिजे. सांप्रत काली युरेनियम (२३८), (T = ४⋅५ X १०९ वर्षे) आणि युरेनियम (२३५), (T = ०⋅७ X १०९ वर्षे) ही मूलद्रव्ये नैसर्गिक युरेनियमामध्ये १४० : १ या प्रमाणात आढळतात. भूविज्ञानीय पुराव्यानुसार सुरुवातीच्या युरेनियम (२३६) या समस्थानिकाचा, त्याचे अर्धायुष्य ०⋅०२ X १०९ वर्षे असल्यामुळे, क्षय होऊन पूर्णपणे लोप झाला आहे. युरेनियमाशिवाय दुसरे दीर्घायुषी मूलद्रव्य म्हणजे थोरीयम (२३२), (T = ४⋅५ x १०९ वर्षे). त्याचे अर्धायुष्य पृथ्वीच्या वयाच्या तिपटीच्या मानाने आहे.
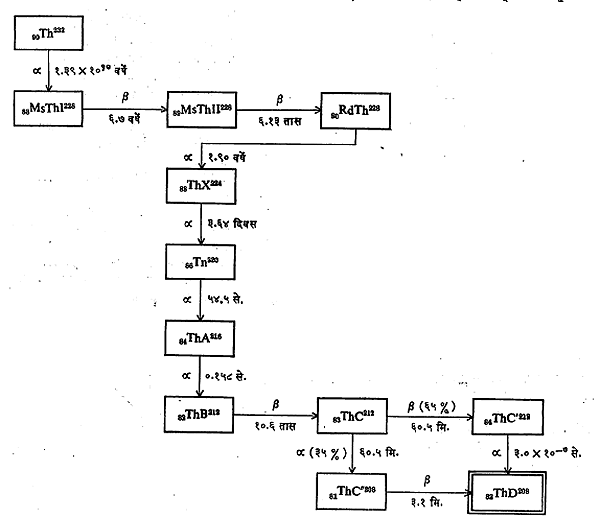
युरेनियमाचा क्षय होताना स्थायी मूलद्रव्य (शिसे) प्राप्त होईपर्यंत मध्यंतरी १४ मूलद्रव्ये प्राप्त होतात. युरेनियम अणूपासून जी मालिका तयार होते त्यामध्ये एकूण आठ α कण व सहा β कण उत्सर्जित होऊन शेवटी शिसे (२०६) हे स्थायी मूलद्रव्य मिळते. या मालिकेत काही मूलद्रव्यांचे अर्धायुष्य अत्यल्प असते. तरीसुद्धा जनक अणूच्या दीर्घायुष्यामुळे दीर्घकालीन समतोलांच्या कल्पनेप्रमाणे अशा अल्पजीवी मूलद्रव्यांना जनक मूलद्रव्य जगविते. रेडॉन वायू युरेनियमाच्या खाणीत आढळतो याचे कारण हेच आहे. थोरियमाच्या मालिकेत १० मूलद्रव्ये आहेत.
या श्रेणीशिवाय काही इतर मूलद्रव्येही नैसर्गिक रीत्या किरणोत्सर्गी असून कोष्टक क्र. २ मध्ये त्यांचे गुणधर्म दिलेले आहेत.
कृत्रिम किंवा प्रवर्तित किरणोत्सर्ग : क्यूरी-झॉल्यो दांपत्याने प्रथम तथाकथित प्रवर्तित किरणोत्सर्गाचा शोध लावला. आता प्रयोगशाळेमध्ये कणांच्या भडिमाराने घडणाऱ्या अणुगर्भ-विघटन क्रियांमध्ये उत्पन्न होणाऱ्या सर्वच किरणोत्सर्गी मूलद्रव्यांना कृत्रिम-किरणोत्सर्गी द्रव्ये म्हणतात आणि या आविष्काराला कृत्रिम किरणोत्सर्ग म्हणतात. उदा., बोरॉन (११) वरील α कणांच्या आघाताने त्यातून प्रोटॉन बाहेर पडतो आणि कार्बन (१४) शिल्लक राहतो. ही विघटन क्रिया B11 (α ,p) C14 अशी थोडक्यात लिहितात. तसेच N14 (n,p) C14 या क्रियेमध्येही C14 उत्पन्न होतो. याचे अर्धायुष्य ५,५७० वर्षे आहे. नायट्रोजनाचे कार्बन (१४) मध्ये रूपांतर विश्वकिरणांतील (बाह्य अवकाशातून पृथ्वीवर येणाऱ्या अतिशय भेदक किरणांतील) न्यूट्रॉनांमुळे निसर्गात सतत होत असते. एकूण नैसर्गिक आणि कृत्रिम मिळून सु. १,००० किंवा अधिक अणुगर्भ प्रकार तयार झालेले आहेत.
कृत्रिम किरणोत्सर्गी द्रव्यांचे उत्पादन : समजा, एखाद्या A या मूलद्रव्यावर वेगवान कणाचा आघात करून कृत्रिम समस्थानिक निर्माण करावयाचा आहे B हे मूलद्रव्य आहे आणि त्याचा क्षयांक λB आहे. उत्पन्न झालेली कार्यप्रवणता BλB = Y/λB (1 –e-λBt) अशी मांडता येईल. येथे Y हा उतारा होय. त्याची व्याख्या अशी आहे उत्पन्न झालेल्या किरणोत्सर्गी द्रव्याची प्रतिसेकंदास (किंवा प्रत्येक तासास) ठराविक प्रयोग परिस्थितीत तयार होणारी कार्यप्रवणता म्हणजे त्या द्रव्याचा उतारा होय. Y ही प्रतिएकक कालात उत्पन्न होणारी कार्यप्रवणता आहे. उदा., सोडियम (२३) वर ड्यूटेरॉनाच्या (हायड्रोजनाच्या ड्यूटेरियम या समस्थानिकाच्या अणुगर्भाच्या) भडिमाराने सोडियम (२४) हे किरणोत्सर्गी मूलद्रव्य निर्माण होते : Na23 (d, p) Na24 ही ती विघटन क्रिया होय. येथे B = Na24; λB = १⋅४४; TB = २१⋅३ तास. ड्यूटेरॉन कणांचा प्रवाह एक मायक्रोअँपिअरचा असेल तर प्रत्येक तासाला Y = ११⋅१ मायक्रोक्यूरी इतका उतारा होईल. जास्तीत जास्त उत्पन्न होणारी कार्यप्रवणता YTB = ०⋅२३६ क्यूरी [→ समस्थानिक].

नैसर्गिक किरणोत्सर्गी श्रेणी : नैसर्गिक किरणोत्सर्गी मूलद्रव्यांच्या तीन श्रेणी उपलब्ध आहेत. (१) युरेनियम (२३८) ने सुरू होणारी (4n+ 2) श्रेणी (आ. २). (२) थोरियम (२३२) ने सुरू होणारी (4n) श्रेणी (आ. ३.). (३) युरेनियम (२३५) ने सुरू (4n + 3) श्रेणी (आ. ४). a उत्सर्जनामुळे द्रव्यमानांक ४ ने कमी होतो, पण b, g उत्सर्जनामुळे त्याच्यात फरक होत नाही, म्हणून एकाच श्रेणीतील मूलद्रव्यांचे द्रव्यमानांक (4n), (4n + 1), (4n + 2), (4n + 3) या पदांनी दाखवता येतात. पैकी (4n+1) ही माला कृत्रिम किरणोत्सर्गी मूलद्रव्यांची आहे. येथे n कोणताही पूर्णांक आहे.नैसर्गिक श्रेणीमधील प्रत्येक समस्थानिकाला दोन नावे मिळालेली आहेत. उदा., मेसोथोरियम-१ (२२८) आणि रेडियम (२२६) हे समस्थानिक आहेत.
(4n+1) ही कृत्रिम किरणोत्सर्गी मूलद्रव्यांची श्रेणी पुढीलप्रमाणे आहे.
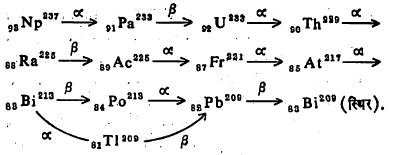
हिला नेपच्यूनियम श्रेणी म्हणतात. या श्रेणीमध्ये अधिकात अधिक अर्धायुष्य (२⋅२ x १०६ वर्षे) नेपच्यूनियमाचे आहे. त्यामुळे पृथ्वीचे वय लक्षात घेता, या श्रेणीचा आतापर्यंत संपूर्ण लोप झाला असला पाहिजे. यामध्ये स्थिर मूलद्रव्य बिरुमथ असून त्यामध्ये ८६ क्रमांकाचे मूलद्रव्य (वायुरूपी रेडॉन) नाही. यातील रेडियम β– किरणोत्सर्गी आहे. या मालेतील क्र. ८५ आणि क्र. ८७ मूलद्रव्यांना १९४७ मध्ये ॲस्टटीन (At) आणि फ्रॅन्सियम (Fr) ही नावे देण्यात आली.
आल्फा उत्सर्जनाने होणारा क्षय : नैसर्गिक α किरणोत्सर्गी मूलद्रव्य स्वभावत:च अस्थायी असली पाहिजेत. α किरणांची ऊर्जा ४ ते १० Mev या सुमाराची असते. कोणत्याही विघटन क्रियेची मीमांसा करताना कोणकोणत्या गोष्टी अक्षय्य किंवा स्थिर राहतात यांचा विचार करावा लागतो. या ठिकाणी अक्षय्यतेचे तीन सिद्धांत लागू पडतात. ते म्हणजे (१) ऊर्जेची अक्षय्यता, (२) संवेगाची (वस्तुमान गुणिले वेग या राशीची) अक्षय्यता आणि (३) विद्युत् भाराची अक्षय्यता. उदा., α विघटन क्रिया पुढील सूत्राने दर्शविता येईल.
ZMA → Z-2MA-4 + 2He4 + Qα ….. …… (१७)
येथे Z = अणुक्रमांक, M = अणुगर्भाचे निश्चित वस्तुमान, A = द्रव्यमानांक, Qα = विघटन उत्पन्न होणारी ऊर्जा म्हणजे α कण आणि अपत्य अणुगर्भ यांची गतिज ऊर्जा.
Qα = [ ZM- (Z-2M + MHe) C2 ….. (१८)
येथे C = प्रकाशाचा वेग. या सूत्रावरून वस्तुमानातील फरक पुरेसा असल्याशिवाय α कणांचे उत्सर्जन होणार नाही हे स्पष्ट होते. साधारणपणे
|
…. ….. (१८अ) |
Ta |
) |
A |
( |
= |
Qα |
|
A-4 |
Tα = α कणाची गतिज ऊर्जा असे मांडता येईल. पहिला प्रश्न असा उत्पन्न होतो की, α कणच का बाहेर पडतात ? प्रोटॉन, न्यूट्रॉन किंवा ड्यूटेरॉन किंवा ऑक्सिजन इ. कण का बाहेर पडत नाहीत ? याचे कारण Qα चे मूल्य हे होय. α कणाची वस्तुमान न्यूनता (वस्तुमानात झालेली घट बंधन ऊर्जा) इतकी मोठी आहे की, ऊर्जेच्या अक्षय्यतेच्या दृष्टीने α चे उत्सर्जन सहज शक्य होते, पण प्रोटॉनाच्या बाबतीत हे शक्य नाही. हे प्रायोगिक रीत्याही स्पष्ट झालेले नाही. α उत्सर्ग अणुक्रमांक ८३ च्या पुढे शक्य आहे. (हाच क्रमांक निश्चित होण्याचा संभव अणुगर्भातील कवचरूपी रचनेशी आहे. अपवाद Pt190, Hf174, Sm147 इ.). ऑक्सिजनाचे उत्सर्जन न होण्याचा संबंध अणुगर्भीय वर्चस (विद्युत स्थिती) अवरोधाशी आहे. शिवाय अणुगर्भांतर्गत कणांचे ऑक्सिजन सदृश गट बनण्याची संभाव्यता अत्यल्प आहे. अणुगर्भीय घटनांचे विवरण अणुगर्भ रचनेच्या निरनिराळ्या प्रतिमानांच्या आधाराने करता येते. यापैकी ‘स्वतंत्र कण किंवा कवचरचना’ आणि ‘द्रवबिंदू’ या दोन प्रतिमानांचा विस्तृत प्रमाणावर उपयोग झाला आहे [→ अणु व आणवीय संरचना].

अणुगर्भीय विघटनांचे विवेचन संयुक्त अणुगर्भाच्या कल्पनेने (उच्च ऊर्जेची विघटने सोडल्यास) उत्तम तऱ्हेने होते. संयुक्त अणुगर्भाचे कणाच्या उत्सर्जनाने विघटन होते, म्हणजे अणुगर्भ क्षोभित अवस्थेत असताना त्यातील मूलकणांमध्ये ऊर्जेची देवाणघेवाण होत असली पाहिजे आणि ज्यावेळी एखाद्या कणाला किंवा कण समूहाला पुरेशी ऊर्जा मिळते तेव्हा तो संयुक्त अणुगर्भातून उत्सर्जित होतो. या उत्सर्जनाच्या क्रियेमध्ये (शोषणाच्या) क्रियेमध्ये अणुगर्भीय वर्चस् अवरोधातून पलीकडे जाण्याचा प्रश्न उपस्थित होतो. रूढ यामिकीनुसार (प्रेरणांची वस्तूवर होणारी क्रिया व त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रानुसार) α उत्सर्जनाची मीमांसा करता येत नाही. पण रदरफर्ड यांच्या α प्रकीर्णनाच्या (विखुरण्याच्या) प्रयोगात अणुगर्भाच्या बाहेरील क्षेत्र कुलंब नियमानुसार असल्याचे दिसून येते. (स्थितिवर्चस् U = Ze/r, r- – त्रिज्यीय अंतर) युरेनियमामधून बाहेर पडणाऱ्या α कणाची ऊर्जा ४⋅२ Mev असते. या α कणाला अपत्य अणू जो थोरियम (९०) त्याच्या वर्चस् अवरोधाला ओलांडून जावे लागेल. या वर्चस् अवरोधाची उंची B (आ. ५) सु. २९ Mev इतकी आहे. त्यामुळे हे अशक्य आहे. अणुगर्भाच्या मध्यापासून एका ठराविक अंतरावर कुलंब प्रतिसारणाचे रूपांतर अणुगर्भीय आकर्षणामध्ये झाले पाहिजे. हे अंतर म्हणजे अणुगर्भाची त्रिज्या R. अणुगर्भीय आकर्षण आणि कुलंब प्रतिसारण मिळून जे वर्चस् क्षेत्र निर्माण होते. त्यामुळे वर्चस् अवरोध तयार होतो (आ. ५).
α कण या वर्चस् अवरोधाच्या आरपार जाण्यासंबंधीचे विवरण तरंगयामिकीच्या [→पुंजयामिकी] साहाय्याने करता येते. तरंगयामिकीनुसार कोणताही ऊर्जायुक्त कण (ज्याची ऊर्जा वर्चस् अवरोधाच्या उंचीपेक्षा कमी असो वा अधिक असो) वर्चस् अवरोधाच्या पलीकडे जाण्याची काही एक निश्चित संभाव्यता असते. α उत्सर्जनाकरिता हे गणित गॅमो, काँडन आणि गर्नी यांनी (१९२८) प्रथम केले. कोणत्याही कणाचे वर्णन त्याच्या द ब्रॉग्ली तरंगाने करावयाचे असून त्याकरिता
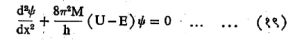
येथे Ψ = तरंगाचे फलन; h = प्लांक स्थिरांक; E = गतिज ऊर्जा; U = एकूण स्थितिवर्चस् व M = कणाचे वस्तुमान आहे. यासारखे श्रोडिंजर समीकरण निरनिराळ्या प्रदेश सीमांवर प्राप्त होण्याच्या अटी सांभाळून सोडवावयाचे असते. कणाच्या गतीचे आकलन संबंधित तरंगाच्या परावर्तन आणि संक्रमण क्रियांच्या रूपाने होते. संक्रमणाची संभाव्यता आणि वर्चस् अवरोधाची भेदनक्षमता (भेदून जाण्याची क्षमता) यांची व्याख्या, संक्रमित तरंगाची तीव्रता (परमप्रसराचा म्हणजे स्थिर स्थितीपासून होणाऱ्या कमाल स्थानांतरणाचा वर्ग) आणि आपाती तरंगाची तीव्रता यांच्या गुणोत्तराने होते. α किरणोत्सर्गी मूलद्रव्याच्या केंद्रामध्ये नेहमीच α कण उपस्थित असतो असे समजण्यास हरकत नाही (संभाव्यता = १) हा कण a जाडीच्या वर्चस् अवरोधावर आघात करीत असतो प्रत्येक आघाताच्या वेळी तो पलीकडे जाण्याची काही एक ठराविक संभाव्यता असते (सुरंग परिणाम).
|
या ठिकाणी आला की, कुलंब |
Zeze |
एकदा का α कण b = |
|
Eα |
|
Zze2 |
प्रतिसारण क्षेत्रामुळे (अणुगर्भापासून दूर गेल्यावर) त्याला Eα = |
|
b |
ही गतिज ऊर्जा प्राप्त होते (आ. ५).
भेदनक्षमता (पार्यता) म्हणजे प्रत्येक आघातास पलीकडे जाण्याची संभाव्यता आणि प्रतिसेकंदास संक्रमण संभाव्यता म्हणजेच मूलद्रव्याचा क्षयांक λ (λ=1/T, माध्य आयुष्याचा व्यस्तांक). श्रोडिंजर समीकरण सोडवून ही भेदनक्षमता किंवा संभाव्यता याकरिता

यांपैकी फक्त पहिलेच पद वापरले, तर स्थूल मानाने भेदनक्षमता मिळते. त्याला गॅमो गुणक G म्हणतात. भेदनक्षमता

गायगर – नटॉल नियम : गायगर व नटॉल यांनी पूर्वीच १९११ मध्ये अर्धायुष्य T चा लॉगरिथम आणि α कणाचा पल्ला यांचा आलेख सरळ रेषेत येतो, असे दाखवले होते. हा पल्ला स्थूलमानाने Eα1⋅5 च्या सम प्रमाणात असतो. तसेच सुरुवातीचा V वेग धरल्यास तो V3 च्या सम प्रमाणात असतो.
पल्ला R = स्थिरांक x V3 = स्थिरांक x Eα1⋅5 … (२६)
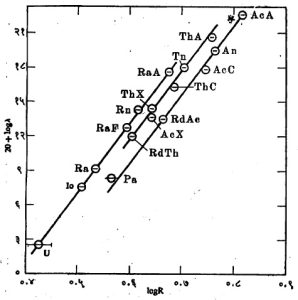
हा गायगर नियम म्हणून प्रसिद्ध आहे. या नियमाप्रमाणे अर्धायुष्य व आल्फाचा सुरुवातीचा वेग किंवा गतिज ऊर्जा यांचा परस्पर संबंध आहे. हे आ. ६ मधील गायगर-नटॉल आलेखात दर्शविले आहे.
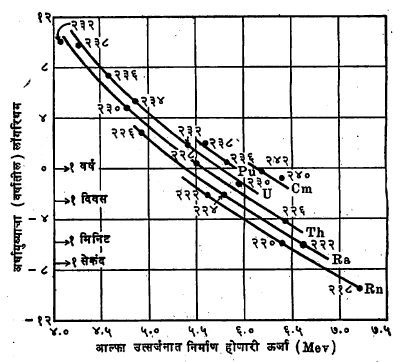
हे आलेख आणि आ. ७ मध्ये दर्शविलेले अर्धायुष्याचा लॉगरिथम व α विघटनात निर्माण होणारी एकूण ऊर्जा (Mev) यांचे, समीकरण (२४) वा (२५) प्रमाणे येणारे आलेख सैद्धांतिक दृष्ट्या एकच आहेत. काँडन, गॅमो आणि गर्नी यांनी गायगर नियम आणि गायगर-नटॉल नियम यांची मीमांसा अणुगर्भीय वर्चस् अवरोधाच्या भेदन क्षमतेच्या कल्पनेला तरंगयामिकीची जोड देऊन उत्तम प्रकारे स्पष्ट केली.
आकृती ७ मध्ये अर्धायुष्याचा लॉगरिथम व α उत्सर्गात उत्पन्न होणारी एकूण ऊर्जा यांचा आलेख दाखविलेले बिंदू प्रायोगिक असून, जोडणाऱ्या रेषा α विघटनाच्या मीमांसेप्रमाणे सैद्धांतिक दृष्ट्या येणाऱ्या आहेत. Z आणि A ची मूल्ये जनक अणुगर्भाची आहेत.
बीटा उत्सर्जनाने होणारा क्षय : उच्च अणुक्रमांकांच्या मूलद्रव्यांचे अस्थैर्य हे α उत्सर्जनाचे कारण आहे. परंतु α उत्सर्जनामुळे अणुक्रमांक २ या संख्येने कमी होतो आणि न्यूट्रॉन/प्रोटॉन संख्या हे गुणोत्तर वाढते. म्हणून उच्च अणुक्रमांकाच्या मूलद्रव्यामध्ये न्यूट्रॉनची संख्या कमी होईल अशी β उत्सर्जनासारखी क्रिया अपेक्षित आहे. मात्र β उत्सर्जन उच्च अणुक्रमांकाच्या अणुपुरतेच मर्यादित आहे असे नव्हे, तर सर्व अणुक्रमांकांमध्ये दोन सममूल्य द्रव्यमानांकांच्या अणुगर्भाशी ही क्रिया निगडित असते. β– किंवा इलेक्ट्रॉनाच्या उत्सर्जनामध्ये अपत्य अणुगर्भाचा अणुक्रमांक १ या संख्येने वाढतो व तो Z+1

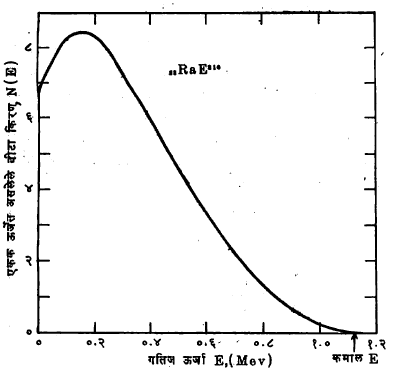
इतका होतो; β+ किंवा पॉझिट्रॉन उत्सर्जनामध्ये किंवा इलेक्ट्रॉन – ग्रास या क्रियेमध्ये तो Z -1 इतका होतो. β कणांचे स्वरूप इलेक्ट्रॉन किंवा पॉझिट्रॉन रूपीच आहे. कर्षुकीय β वर्णपटलेखकाच्या साहाय्याने β कणांचे ऊर्जामापन करता येते. β कणांच्या ऊर्जावितरण आलेखाला β वर्णपट म्हणतात. हा वर्णपट अखंड आढळतो. म्हणजे एका महत्तम ऊर्जामूल्याच्या Eβmax खाली शून्यापर्यंत निरनिराळ्या ऊर्जांचे β कण आढळतात. अशा नमुन्याचा 83RaE210 मूलद्रव्याचा β वर्णपट आ. ८ मध्ये दाखविला आहे.
काही वर्णपटांमध्ये या अखंड वर्णपटावर काही ‘शृंगे’ अधिष्ठापित झालेली आढळतात. त्यांचा संबंध अणुगर्भबाह्य इलेक्ट्रॉनाशी असल्यामुळे त्यांना शुद्ध β कण म्हणता येत नाही. β उत्सर्जन क्रियेमध्ये उत्पन्न होणारी ऊर्जा Qβ पुढील सूत्राने मिळते.
zMA – z+1 MA – m0 = Qb …. …… (२७)
( M ही अणुगर्भीय द्रव्यमाने, m0 इलेक्ट्रॉनाचे द्रव्यमान), आणवीय द्रव्यमाने वापरल्यासzMA – z+1 MA – m0 = Qb असे सूत्र मिळेल म्हणून सर्व β कण एका निश्चित Qβ ऊर्जेचे असावयाला हवेत. प्रायोगिक रीत्या मात्र Eβmaxफक्त Qβ च्या समान असते आणि सरासरी β कण ऊर्जा त्याच्या सु. १/३ असते. Qβ – Eβ या ऊर्जेतील फरकांची संगती लागली पाहिजे ती कशी लागते ते पुढे न्यूट्रिनो व प्रतिन्यूट्रिनो यांच्या संबंधात दिले आहे. अपत्य गुणधर्म आणि β कण यांमध्येच संवेगाचा विनिमय होणार असेल तरच सर्व β कणांची ऊर्जा एकसारखी Qβ इतकी मिळेल.
न्यूट्रिनो आणि प्रतिन्यूट्रिनो : ज्या अर्थी β कणांचा अखंड वर्णपट मिळतो त्या अर्थी संवेगाच्या अक्षय्यतेच्या तत्त्वाने β उत्सर्जनामध्ये तीन कणांचा अंतर्भाव झाला पाहिजे. ऊर्जेची अक्षय्यता व संवेगाची अक्षय्यता यांच्याशी सुसंगत अशी संकल्पना प्रथम पाउली यांनी १९३१ च्या सुमारास सुचविली. हा तिसरा कण विद्युत् भाररहित जवळजवळ वस्तुमानरहित
| परंतु अंगभूत परिवलन (कोनीय संवेग) | 1 | . | h | असणारा |
| 2 | 2π |
असा असला पाहिजे, ही ती संकल्पना होय (h हा प्लांक स्थिरांक होय). फेर्मी यांनी पुढे या कणाला न्यूट्रिनो हे नाव दिले. न्यूट्रिनो (v) हा पॉझिट्रॉन उत्सर्जनाशी संबंधित असतो आणि प्रतिन्यूट्रिनोचा (v–) संबंध इलेक्ट्रॉन उत्सर्जनाशी येतो. या दोहोंमध्ये फरक फक्त परिवलनाच्या दिशेमध्ये असतो. कोणतीही β– उत्सर्जन क्रिया म्हणजे अणुगर्भातील न्यूट्रॉनमधून होणाऱ्या β– उत्सर्जनाचीच क्रिया होय. जसे
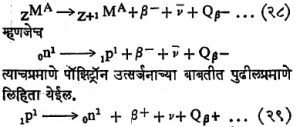

पाउली यांच्या संकल्पनेप्रमाणे Qβ ही ऊर्जा महत्तम β ऊर्जेबरोबर असली पाहिजे. असे असेल त्यावेळी ν ऊर्जा शून्य असेल आणि β ऊर्जा शून्योपयोगी असेल तेव्हा v ऊर्जा Qβ इतकी वाढेल. कोणत्याही β साठी Eb + En = Eβmax. पुंजयामिकितील ⇨ अनिश्चिततेच्या तत्त्वाप्रमाणे इलेक्ट्रॉन निर्माण झाल्यावर तो अणुगर्भात राहणे अशक्य आहे म्हणून तो बाहेर पडतो. प्रायोगिक निरीक्षणांशी सुसंगत अशी β उत्सर्जनाची उपपत्ती १९३४ मध्ये फेर्मी यांनी प्रथम सुचविली (त्यावेळी न्यूट्रिनो आणि प्रतिन्यूट्रिनो हा भेद ज्ञात नव्हता). या उपपत्तीप्रमाणे इलेक्ट्रॉन आणि न्यूट्रिनो हे दोन्हीही अणुगर्भात निर्माण होतात आणि त्यांचे उत्सर्जन होते. फेर्मी उपपत्तीप्रमाणे W ऊर्जा असणाऱ्या β कणांची संख्या N (W) पुढील सूत्राने मिळते.

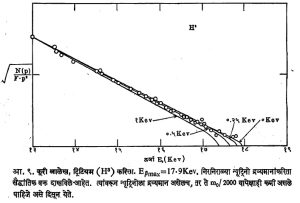
W व W + dW यांमध्ये एकूण ऊर्जा असणाऱ्या β कणांची संख्या, F (Z, W) फेर्मी फलन lPl2 संक्रमणाचा वर्ग केलेला आव्यूह घटक T0 = व एक स्थिरांक. β वर्णपटाच्या आकाराचा न्यूट्रिनोच्या द्रव्यमानाशी (mv शी) फार संबंध आहे. शून्य धरल्यास आणि β कणांची संख्या N(p), संवेग p च्या वितरणाच्या दृष्टीने मांडल्यास ![]() मूल्याचा व E यांचा काढलेला आलेख सरळ रेषात्मक असला पाहिजे. ट्रिटियम (H3) करिता हा आलेख आ. ९ मध्ये दिला आहे. अशा आलेखांना एफ्. एन्. कूरी या संशोधकांचे नाव दिले आहे.
मूल्याचा व E यांचा काढलेला आलेख सरळ रेषात्मक असला पाहिजे. ट्रिटियम (H3) करिता हा आलेख आ. ९ मध्ये दिला आहे. अशा आलेखांना एफ्. एन्. कूरी या संशोधकांचे नाव दिले आहे.
विशिष्ट β उत्सर्जनाचा β वर्णपट फेर्मी उपपत्तीशी कितपत मिळताजुळता आहे हे कूरी आलेखांवरून समजते. १९३३ मध्ये सार्जेट यांनी काढलेल्या काही विशिष्ट आलेखांवरून असे दिसून आले की, नैसर्गिक β उत्सर्जकांचे सामान्यत: दोन प्रकार होतात.
या गोष्टीचा खुलासा करण्यासाठी गॅमो यांनी अशी कल्पना मांडली की, β उत्सर्जनाला जबाबदार असणारी अणुगर्भीय संक्रमणे दोन प्रकारची असली पाहिजेत. या संक्रमणांना त्यांनी अनुमत (आडकाठी नसलेले) व निषिद्ध (आडकाठी असलेले) ही नावे दिली. अनुमत संक्रमणासाठी समी. (३०) मधील lPl2 या राशीचे मूल्य १ असते. कृत्रिम β उत्सर्जकाच्या विशेष अभ्यासावरून या कल्पनेत आणखी फेरफार करणे भाग पडले व निषिद्ध संक्रमणाच्या पहिली, दुसरी व तिसरी अशा श्रेणींमध्ये वर्गीकरण करण्यात आले आणि अनुमत व निषिद्ध संक्रमणाच्या सर्व श्रेणींचे अनुगृहीत व नानुगृहीत असे प्रत्येकी देान उपविभाग पाडण्यात आले. समी. (३०) मधील फेर्मी फलन F (Z, W) व उत्सर्जकाचे अर्धायुष्य यांच्या गुणाकाराला ‘तौलनिक अर्धायुष्य’ (ft) ही संज्ञा दिली आहे. अनुमत – अनुगृहीत संक्रमणासाठी ft = १,००० ते ५,००० सेकंद, अनुमत – नानुगृहीतासाठी ft = ५,००० ते ५,००,००० से. येतात. पहिल्या श्रेढीच्या निषिद्ध संक्रमणासाठी ft = १०६ ते १०८ से. आणि त्यावरच्या श्रेढीसाठी ft याहून जास्त येईल. म्हणजे ft मूल्यावरून आपणाला संक्रमणाचा प्रकार कळू शकतो.
न्यूट्रिनो आणि प्रतिन्यूट्रिनो यांचे अस्तित्व : हा विषय आणि त्याचप्रमाणे न्यूट्रिनोचे दोन प्रकार – इलेक्ट्रॉन विशिष्ट आणि μ मेसॉन विशिष्ट – यांविषयीचे संशोधन अगदी अलीकडचे आहे. येथे फक्त काही मर्यादित गोष्टीचाच उल्लेख केला आहे. कूरी आलेखावरून न्यूट्रिनोचे वस्तुमान अत्यल्प श्रेणीचे (<×m0/2000) असले पाहिजे हे अनुमान निघते.
β कण व प्रतिक्षेपित (मागे उलटलेला) अपत्य गुणधर्म यांच्या संवेगाच्या मापनाने न्यूट्रिनोच्या संवेगाचे गणित करता येते आणि त्यावरून त्याची ऊर्जाही मिळते. तिच्यावरू येणारा न्यूट्रिनोचा वेग c या प्रकाशाच्या वेगाइतका आढळतो, म्हणून त्याचे द्रव्यमान जवळजवळ शून्य असले पाहिजे. अशा प्रकारचे शरविन यांचे प्रयोग आणि इलेक्ट्रॉन-ग्रास क्रियेचे ॲलन यांचे प्रयोग यांवरून न्यूट्रिनोचे अस्तित्व सिद्ध होते. यापेक्षाही प्रतिन्यूट्रिनाच्या अस्तित्वाविषयी प्रत्यक्ष प्रमाण राइनेस आणि कॉवन यांच्या १९५३ मध्ये सुरू झालेल्या आणि अखेरीस १९५६ मध्ये प्रसिद्ध झालेल्या प्रयोगात मिळते. या प्रयोगात प्रतिन्यूट्रिनोची अणुविक्रियांतून उत्पत्ती, त्यांच्या प्रोटॉनवरील विक्रियेत उत्पन्न होणारे न्यूट्रॉन व पॉझिट्रॉन न्यूट्रॉनाचा कॅडमियमामध्ये ग्रास व γ ची उत्पत्ती आणि पॉझिट्रॉन-इलेक्ट्रॉन यांच्या संयोगाने γ ची उत्पत्ती या सगळ्यांची नीट संगती लागते.
न्यूट्रिनोचे एरव्ही अस्तित्व ओळखणे कठीण व जवळजवळ अशक्यच आहे कारण कोणत्याही विक्रियेशिवाय सूर्यामधून ते आरपार जाऊ शकतात. त्यांची संख्या ३७ टक्के होण्यासाठी १०० प्रकाशवर्षे इतक्या जाडीचे शिसे लागेल ! मात्र वर उल्लेखिलेल्या प्रयोगावरून पाउली यांची न्यूट्रिनोची संकल्पना आता निव्वळ सैद्धांतिक राहिली नसून ती प्रयोगाने सिद्ध झाली आहे.
गॅमा किरणोत्सर्ग : विद्युत् चुंबकीय प्रारणाचे नामाभिधान त्याच्या उगमावरून ठरविले पाहिजे. निव्वळ ऊर्जेवरून वर्गीकरण केले तर ते सोईस्कर होणार नाही. हे प्रारण कणमय असते अशा ऊर्जाकणांना फोटॉन म्हणतात. क्षुब्धावस्थेतील अणुगर्भापासून उत्सर्जित झालेल्या प्रारणालाच γ किरण म्हणतात. किरणोत्सर्गी अणुगर्भामधून α किंवा β यांचे उत्सर्जन होते, तेव्हा अपत्य अणुगर्भ किंवा मूळचे जनक अणुगर्भ क्षुब्धावस्थेत असण्याचा संभव असतो. विद्युत् चुंबकीय प्रारणाच्या उत्सर्जनाने क्षुब्ध अणुगर्भाला स्थैर्यावस्था प्राप्त होते. किरणोत्सर्गी अणुगर्भातून निघणाऱ्या γ फोटॉनाची ऊर्जा २⋅६२ Mev पर्यंत असू शकते. γ किरणांचा नेहमी रेखा वर्णपट असतो. γ किरणांची तरंगलांबी आणि ऊर्जा ब्रॅग यांच्या स्फटिक वर्णलेखकाच्या [→ स्फटिकविज्ञान] साहाय्याने निश्चित करता येतात.
अणुगर्भ फोटॉन व्यवस्थेमध्ये फोटॉनाच्या क्षेपण क्रियेत एकंदर कोनीय संवेग अक्षय राहिला पाहिजे. कोनीय संवेगाचे एकक h/2π घेतल्यास संवेग पुजांकामध्ये मांडता येतो. फोटॉनाच्या अंगभूत परिवलनाचा संवेग पुंजांक १ असतो. अणुगर्भाच्या या Ι कोनीय संवेगाच्या पुंजांकामध्ये ΔΙ हा बदल ± १ असेल तर γ उत्सर्जन सहज शक्य होते. या क्रियेचे सरासरी आयुर्मान १०-१६ से. या मानाचे असते. ΔΙ = 0 ही क्रिया अशक्य आहे. ΔΙ = ± २ किंवा अधिक असेल, तर त्यामानाने ती क्रिया निषिद्ध असते. पुंजयामिकीप्रमाणे γ उत्सर्जनाचे वर्णन आणि वर्गीकरण कोनीय संवेगाच्या बदलावरून करतात. ΔΙ = १ यांचे वर्णन द्विध्रुवी प्रारण ΔΙ = २ असेल तर चतुर्ध्रुवी प्रारण, ΔΙ = ३ असेल तर अष्टध्रुवी प्रारण, असे करतात. अणुगर्भाची सुरुवातीची अवस्था आणि अखेरची अवस्था यांमधील कोनीय संवेगातील फरकावरून ध्रुवाचा क्रम ठरतो. याशिवाय या संक्रमणक्रियांचे विद्युत ध्रुवी आणि कर्षुक ध्रुवी असे वर्गीकरण होते.
गॅमा संक्रमण क्रियेचे सरासरी आयुर्मान : अनेकध्रुवी संक्रमणाची संभाव्यता अल्प असते. उदा., १ Mev गॅमा उत्सर्जन व्हावयाचे असेल आणि ΔΙ = २ असेल तर सरासरी आयुर्मान १०-११ से. असेल. परंतु ΔΙ = ५ करता ते सु. १ वर्ष असेल. हे झाले विद्युत् ध्रुवी संक्रमणासंबंधी कर्षुक ध्रुवी संक्रमणाचे आयुर्मान वाइसकॉफ यांच्या उपपत्तीप्रमाणे 4.4 A 2/3 या पटीने अधिक असते.
अंतर्गत रूपांतर : अखंड β कण वर्णपटावर काही वेळा एका निश्चित ऊर्जेच्या β कणांची शृंगे आढळतात. हे β कण खरोखरी अणुगर्भबाह्य इलेक्ट्रॉन असून अंतर्गत रूपांतर क्रियेमुळे ते सोडले जातात, क्षुब्ध अणुगर्भाची जादा ऊर्जा अणुगर्भबाह्य बद्ध इलेक्ट्रॉनाला मिळून त्याचे उत्सर्जन होते. अणुगर्भीय अनेकध्रुवी क्षेत्र आणि बद्ध इलेक्ट्रॉन यांमधील या अन्योन्य क्रियेला अंतर्गत रूपांतर क्रिया म्हणतात. एरव्ही या क्षेत्रामुळे γ चे प्रारण व्हावयास पाहिजे. अंतर्गत रूपांतर क्रियेची γ प्रारणाशी नेहमी स्पर्धा असते. अंतर्गत रूपांतराची संभाव्यता आणि γ क्षेपणाची संभाव्यता यांच्या गुणोत्तराला अंतर्गत रूपांतराचा गुणक (α) म्हणतात. α=Ne/Nr
येथे Ne = अंतर्गत रूपांतर इलेक्ट्रॉनांची संख्या आणि Nr = त्याच कालात होणारी प्रोटॉनांची संख्या. अणुगर्भीय ऊर्जा पातळींवरील ऊर्जेचा फरक Wα चे इलेक्ट्रॉनाच्या ऊर्जेमध्ये रूपांतर होते म्हणून निरनिराळ्या K, L, M वगैरे कवचांमध्ये सिद्ध असणाऱ्या इलेक्ट्रॉनांची गतिज ऊर्जा
Eβ = W – Ei ; [ i = K, L, M वगैरे ],
या सूत्राने मिळेल. Eβ च्या मापनाने EK – EL वगैरे K, L इ. कवचांतील बंधन ऊर्जांमधील फरक अचूकपणे काढता येतो आणि त्यावरून अणुक्रमांकही ठरवता येतो.
समघटक संक्रमणे : मितस्थायी अवस्था : बीटा उत्सर्जनानंतर जे अणुगर्भ मितस्थायी पोहोचतात त्यांना समघटक गुणधर्म म्हणतात. γ क्षेपण किंवा β उत्सर्जन काही कारणाने निषिद्ध असल्यामुळे हे घडते. मितस्थायी अवस्थांतील अणुगर्भातील γ किरण किंवा रूपांतरित इलेक्ट्रॉन किंवा या क्रियांना फार विलंब होणार असेल, तर β उत्सर्जनही संभवते. मितस्थायी अवस्था किंवा स्थिरावस्था यांतील कोनीय संवेगाचा फरक ΔΙ हा २ पेक्षा बराच अधिक असला तर ही घटना घडते. बेरियम (१३७) च्या उदाहरणाने याचे स्पष्टीकरण होईल. तळस्थितीची ऊर्जा पातळी आणि समघटकाची क्षोभित पातळी यांमध्ये ०⋅६६ Mev इतका फरक आहे व कोनीय संवेग फरक ४ आहे. क्षोभित पातळीचे अर्धायुष्य २⋅६ मिनिटे आहे. क्षोभित पातळीपासून त्याच्या (Ba137 च्या) तळस्थितीत येताना ०⋅६६ Mev विलंबित गॅमा किरण व रूपांतरीत इलेक्ट्रॉन यांचे उत्सर्जन होते.
कृत्रिम रीत्या समघटक अणुगर्भाची निर्मिती प्रथम ब्रोमीन (८०) ची झाली. ब्रोमीन (७९) वर मंदगती न्यूट्रॉनांच्या भडिमाराने ब्रोमीन (८०) निर्माण होतो. त्यामधून β कण बाहेर पडतात पण दोन अर्धायुष्य ४⋅४ तास आणि १८ मिनिटे अशी आढळतात. याची मीमांसा तळस्थिती आणि समघटक क्षोभित पातळी अशा दोन पातळ्यांच्या अस्तित्वाने करता येते. मितस्थायी Br80 (समघटक) मधून उत्सर्जनाने Br80 (स्थिर) निर्माण होतो. या क्रियेचे अर्धायुष्य ४.४ तास आहे. Br80 (स्थिर) मधून उत्सर्जन होते. त्याचे अर्धायुष्य १८ मिनिटे आहे. लवकरच मितस्थायी Br80 आणि Br80 (स्थिर) मध्ये किरणोत्सर्गी चिरस्थायी समतोल निर्माण होऊन β उत्सर्जनाचे अर्धायुष्य समघटक संक्रमणाच्या अर्धायुष्याइतके आढळते. समघटक अणुगर्भ विषम प्रोटॉन वा विषम न्यूट्रॉन असणाऱ्या विषम द्रव्यमानांकाच्या मूलद्रव्यांत विशेषत: आढळतात.
मॉसबावर परिणाम : अनुस्पंदन (दोन सारख्या कंपन संख्यांमुळे होणारा एकमेकांचा प्रतिसाद) ही घटना भौतिकीच्या सर्व शाखांमध्ये परिचित आहे. अणुगर्भातून बाहेर पडणाऱ्या γ किरणांच्या बाबतीतही ही घटना अपेक्षित आहे. γ फोटॉनाची कंप्रता (दर सेकंदास होणारी कंपनसंख्या) ν अणुगर्भपातळ्यांमधील ऊर्जेच्या फरकाच्या रूपात मिळते ती अशी : hν = Eex – Eg. येथे h = प्लांक स्थिरांक, Eex = क्षुब्ध पातळीची ऊर्जा, Eg = तळपातळीची ऊर्जा. ν कंप्रतेचे हे फोटॉन त्याच प्रकारच्या अणुगर्भावर आघात करतील तर त्याचे अनुस्पंदन आविष्काराप्रमाणे शोषण होऊन, तो अणुगर्भ क्षोभित व्हावयास हवा आणि पुन्हा तो γ फोटॉन उत्सर्जित व्हावयास हवा. पण अशी घटना क्वचित घडते. याचे कारण असे की, फोटॉन उत्सर्जित होताना प्रतिक्षेपित अणुगर्भाला ER ही ऊर्जा मिळते
| [ | ER = | P2 | ; p = | hv | व M अणुगर्भाचे द्रव्यमान | ] |
| 2M | c |
म्हणजे v कंप्रता (Eex – Eg)-ER यांच्याशी सुसंगत असेल. त्याचप्रमाणे शोषणाच्या वेळी अणुगर्भास (Eex – Eg)+ER इतकी ऊर्जा द्यावी लागेल म्हणून या दोन ऊर्जांमध्ये 2ER ~ 0⋅1 ev चे अंतर पडते. आता ν कंप्रतेच्या वर्णरेषेचे रूंदावणे ⇨ डॉप्लर परिणामांवर आणि अनिश्चिततेच्या तत्त्वानुसार होणाऱ्या संक्रमणाच्या आयुर्मानावर अवलंबून असते. पैकी दुसऱ्या कारणाने होणारे रुंदावणे 0⋅4ev च्या मानाचे असते आणि डॉप्लर रुंदावणे
| Δv = v. | v | इतके असते. ऊर्जा विस्तार | ΔE = E. | v |
| c | c |
हा तापमानावर अवलंबून असतो. त्यामुळे अनुस्पंदन साधण्याकरिता ΔE ~ 0⋅1 ev या मानाचा करण्यासाठी तपमान T ~ १,२००० के.(केव्हिन निरपेक्ष तपमान) या मानाचे हवे. वर उल्लेख केल्याप्रमाणे प्रतिक्षेपणाची ऊर्जा p2/2M इतकी असते. येथे M हे अणुगर्भाचे (किंवा अणूचे) द्रव्यमान होय. M जेवढे मोठे तेवढे प्रतिक्षेपणाची (ऊर्जा कमी. गॅमाचा उगम असणारा अणू एखाद्या स्फटिकात बद्ध असेल, तर M जवळजवळ त्या स्फटिकाच्या द्रव्यमानाइतके होईल आणि म्हणून अणूच्या द्रव्यमानाशी तुलना करता ते अनंत (∞) समजावयसा हरकत नाही. त्यामुळे वर्णरेषा रुंदावणे शून्यप्राय होईल. म्हणून अशा प्रारणास किंवा शोषणास प्रतिक्षेपरहित प्रारण वा शोषण म्हणतात. हा शोध मॉसबावर यांनी १९५८ मध्ये लावला. म्हणून यास मॉसबावर परिणाम म्हणतात. प्रतिक्षेपरहित गॅमा फोटॉनाचे शोषण असे थोडक्यात मॉसबावर परिणामाचे वर्णन करता येईल.
किरणोत्सर्गी कार्यप्रवणतेची एकके व प्रमाण मापे : कार्यप्रवणतेचे एकक क्यूरी : ज्या किरणोत्सर्गीय द्रव्यामध्ये प्रतिसेकंदास ३⋅७ x १०१० इतकी अणुविघटने होतात त्या द्रव्याची कार्यप्रवणता म्हणजे एक क्यूरी होय. जुन्या क्यूरी एककाशी हे एकक जुळते असावे म्हणून ३⋅७ हा गणक स्वेच्छ निवडलेला आहे. याप्रमाणे एक ग्रॅम रेडियमाची कार्यप्रवणता बऱ्याचशा प्रमाणात एक क्यूरी आहे असे म्हणता येते. कोणत्याही द्रव्याच्या, विशेषत: ज्यातून α उत्सर्जन होत नाही, अशा द्रव्याच्या विघटनाची केवल त्वरा निश्चित करणे मोठे किचकट व अवघड काम आहे. विघटनक्रियेचे संपूर्ण ज्ञान म्हणजे β आणि γ वर्णपटाचे संपूर्ण ज्ञान होय आणि प्रत्येकाची एकंदर उत्सर्जनामधील टक्केवारी आणि किरणांची ऊर्जा यांचे ज्ञान असणे आवश्यक आहे. तुलनात्मक अभ्यासाकरिता वरील कारणांमुळे आणि प्रयोगासाठी लागणाऱ्या कालाच्या मानाने अतिदीर्घ (जवळजवळ अनंत) असणाऱ्या अर्धायुष्यामुळे (१,६२० वर्षे) रेडियम हे मूलद्रव्य, प्रमाण मापाकरिता उपयुक्त ठरले आहे. अंती किती अणुविघटने होतात हे प्रत्येक पदार्थाकरिता तुलनेने निश्चित करावयाचे असते.
राँटगेन : हे प्रारणाच्या ऊर्जेचे एकक आहे. मुळात जीवशास्त्रीय परिणामाच्या मात्रामापनाचे एकक म्हणून याची निर्मिती झाली. १९३७ मध्ये शिकागो येथे रेडिऑलॉजिकल काँग्रेसमध्ये राँटगेन एककाची (r) नवीन व्याख्या करण्यात आली. ती अशी : ज्या क्ष-किरण किंवा γ किरणराशीमुळे संबंधित प्रत्येक ०⋅००१२९३ ग्रॅम (०० से.तपमान व १ वातावरण दाब) हवेत कणरूपी उत्सर्जनाने हवेमध्ये उत्पन्न होणाऱ्या ऋण किंवा धन विद्युत् भार असणाऱ्या आयनांचा (विद्युत् भारित अणू, रेणू वा अणुगट यांचा) एकत्रित (ऋण आयनांचा किंवा धन आयनांचा) विद्युत् भार एक स्थिर विद्युत् एकक (इलेक्ट्रो स्टॅटिक यूनिट) इतका असतो ती राशी. म्हणून एक r मुळे प्रमाण तपमान (०० से.) व दाब (१ वातावरण दाब) असणाऱ्या एक ग्रॅम हवेत १⋅६१ x १०१२ आयने युग्मे तयार होतात. याप्रमाणे एक r एककामुळे हवेमध्ये प्रतिग्रॅम ८३⋅८ अर्ग इतक्या ऊर्जेचे शोषण होते. राँटगेन हे आयनीकरणाचे एकक आहे. म्हणून γ किरण मात्रेचे मापन प्रतिसेकंद राँटगेन यांनी करावयास हवे. या एककाने किती ऊर्जा आपातित झाली (पडली) याचा बोध न होता किती ऊर्जेचे शोषण झाले याचा बोध होतो.
रॅड : हे शोषित प्रारणाच्या मात्रेचे एकक असून ते शोषक द्रव्याच्या एक ग्रॅममध्ये १०० अर्ग ऊर्जा असणाऱ्या प्रारणाच्या मात्रेबरोबर असते. हे एकक सर्व प्रकारच्या प्रारणांना व कणांना लागू आहे. स्नायूचा प्रत्येक घन मायक्रॉनमध्ये (१ मायक्रॉन = १०-४ सेंमी). सु. दोन आयनीभूत रेणू आणि सु. तितकेच क्षोभित रेणू एका रॅडमुळे उत्पन्न होतात.
राँटगेन भौतिक सममूल्य (rep) : हे किरणोत्सर्गाच्या मात्रेचे माप आहे. एक राँटगेन γ प्रारणाची हवेमध्ये जितकी ऊर्जा शोषली जाते तितकीच ऊर्जा स्नायुतंतूमध्ये आयनीकरणामुळे शोषली गेली, तर त्या मात्रेस राँटगेन भौतिक सममूल्य म्हणतात.
१ r (फोटॉन) = १ rep हे अगदी स्थूल असे विधान आहे.
राँटगेन मानव सममूल्य (rem) : किरणोत्सर्गीय सापेक्ष जीवशास्त्रीय परिणाम (RBE) हा किरणांचा प्रकार आणि जीवशास्त्रीय पदार्थ यांवर अवलंबून असतो. हा परिणाम एकाच प्रारणाकरिता ०⋅५ ते २० पट इतका निरनिराळा आढळतो. RBE न्यूट्रॉन/ RBE गॅमा हे गुणोत्तर ४ ते १० असू शकते. एक r गॅमा किंवा क्ष-किरणामुळे मानवी शरीरात जो परिणाम होतो तोच परिणाम स्नायुतंतूमध्ये (अंदाजे) जी ऊर्जा शोषण झाल्यामुळे होतो त्यास राँटगेन मानव सममूल्य म्हणतात.
| १ rem = | ८३ अर्ग | = ०.२ rep |
| RBE स्नायुतंतू ग्रॅम |
राँटगेन प्रतितास मीटर (rhm) : एक मीटर अंतरावर प्रतितास राँटगेन हे एकक किरणोत्सर्गी द्रव्याच्या तीव्रतेचे दर्शक आहे. विघटन क्रियेचा तपशील ज्ञात असो वा नसो γ किंवा क्ष-किरण उत्सर्ग करणाऱ्या किरणोत्सर्गी द्रव्याच्या एकूण राशीचे ते निर्देशक आहे. rhm हे वैद्यकीय, जीवशास्त्रीय मात्रेचे किंवा संरक्षणमापनाचे एकक नव्हे. उदा., १ ग्रॅम रेडियम = ०⋅९६९ rhm. राँटगेन प्रतितास मीटरामध्ये मापलेले मूल्य रेडियमाच्या कार्यप्रवणतेवर अवलंबून आहे. १ rhm कोबाल्ट (६०) अनावृत्त (आवरणाने वेष्टित नसलेले) असेल तर एक मीटर अंतरावर प्रतितासास १ r आयनीकरण (हवेमध्ये) उत्पन्न करील. तेच शिशाच्या आवरणाने वेष्टित असेल आणि एक मीटर अंतरावर ०⋅१ r इतकेच आयनीकरण प्रतितास होत असेल, तर आवृत्त (वेष्टित) किरणोत्सर्गीय द्रव्याची तीव्रता ०⋅१ rhm इतकी असेल.
मात्रामापन, मात्रा एकके : किरणोत्सर्गी पदार्थापासून निघणाऱ्या किरणांमुळे मिळणाऱ्या मात्रेचे मापन करण्यास मात्रामापन म्हणतात. मात्रामापन करणाऱ्या उपकरणास मात्रामापक म्हणतात. प्रयोगशाळेत, कारखान्यात अथवा अणुविक्रियक (अणुभट्टी) असलेल्या ठिकाणी काम करणाऱ्या लोकांना वैयक्तिक सूचना मिळण्यासाठी आणि संरक्षक उपाय योजण्यासाठी व्यक्तिगत उपकरणे वापरावी लागतात ती अशी :
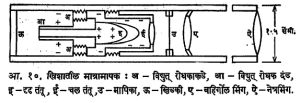
(१) छायाचित्रण फिल्म असलेला बिल्ला : हा मनगटाशी, छातीवर वा कमरेशी बाळगता येते. आयनीकरणामुळे छायाचित्रण फिल्मवर परिणाम होतो व ती धुवून विकाशित केल्यास तिच्या काळसरपणाच्या तीव्रतेवरून मात्रेचे अनुमान होते. β, γ व क्ष-किरण यांकरिता याचा चांगला उपयोग होतो. परंतु फोटॉन, वेगवान न्यूट्रॉन यांकरिता ही पद्धत उपयोगी पडत नाही. (२) खिशातील मात्रामापक : हा फाउंटनपेनच्या आकाराचा असून खिशात ठेवता येतो. त्याचे कार्य लॉरिटसेन विद्युत् दर्शकाप्रमाणे आयनीकरण पात्रांमध्ये उत्पन्न होणाऱ्या विद्युत्भाराच्या मापनावर अवलंबून असते. आ. १० मध्ये (इ) हा धातुविलेपन केलेला क्वॉर्ट्झाचा तंतू आणि (ई) तसाच सूक्ष्मचलनक्षम क्वॉर्ट्झाचा तंतू हे दोन्ही U अशा आकारात वळवून टोकाशी जोडले आहेत. उपकरणामध्येच सूक्ष्मदर्शकाचा अंतर्भाव आहे. (ऊ) या खिडकीतून प्रारण आत येते. त्याच्यावर नेहमी एक संरक्षक आच्छादन असते. हे झाकण काढून विद्युत् घटमालेच्या साहाय्याने बाहेर असणाऱ्या अग्रांच्या द्वारा तंतूंना विद्युत् भार देता येतो. तंतूंची प्रतिमा (उ) या मापिकेवरील शून्य वा खुणेवर आणता येते. आयनीकरणामुळे विद्युत् भार कमी कमी होत जातो आणि तंतूंच्या विचलनावरून मात्रेचे अनुमान करता येते. अशी उपकरणे चांगली मजबूत असून हालचालीमुळे किंवा कधी खाली पडली तरी ती नादुरुस्त होत नाहीत. (३) विवर्ण होणारी रंगीत काच : एका विशिष्ट प्रकारच्या काचेतील रंगमय द्रव्यावर आयनीकरणाचा परिणाम होऊन त्याची छटा बदलते. प्रमाण छटेशी या वर्णछटेची तुलना करून मात्रेचे अनुमान करता येते. (४) किरणोत्सर्गी परीक्षा, पहाणी किंवा मापन यंत्रामध्ये मुख्यत: गायगर-म्यूलर गणित्राचा उपयोग करतात. त्यावरून उत्पन्न झालेला विद्युत् भार किंवा प्रतिमिनिटास मोजलेली कणसंख्या कळते [→ कण अभिज्ञातक].
किरणोत्सर्गापासून संरक्षण कसे करावे, सह्य मात्रा किती इत्यादींचा विचार [→प्रारण जीवविज्ञान (विविध आयनीकारक प्रारणांचा जीवसृष्टीवर कोणता परिणाम होतो याचा अभ्यास करणारे विज्ञान)] या स्वतंत्र शाखेत करण्यात येतो. अणुबाँबच्या स्फोटानंतर निर्माण होणाऱ्या किरणोत्सर्गी धुळीसंबंधी ⇨किरणोत्सर्गी अवपास या नोंदीत माहिती दिली आहे. अणुगर्भीय विक्रियकांत निर्माण होणारे किरणोत्सर्गी द्रव्य व त्याची विल्हेवाट लावण्याची समस्या हेही महत्त्वाचे प्रश्न आहेत [→ अणुकेंद्रीय अभियांत्रिकी].
उपयोग : किरणोत्सर्गाचा उपयोग विविध क्षेत्रांमध्ये दोन प्रकारांनी करता येतो. एकतर किरणोत्सर्गी द्रव्यांमधून निघणाऱ्या किरणांची मात्रा मर्यादित कालापर्यंत देऊन त्याच्या अनिष्ट परिणामाचा उपयोग रोगट कोशिकांचा (पेशींचा) नाश करून निरोगी कोशिका वाढविण्यास साहाय्य करण्याकडे करता येतो. असा उपयोग जीवशास्त्र, वैद्यक, शेतीविषयक समस्या यांमध्ये करता येतो. दुसरा प्रकार म्हणजे किरणोत्सर्गी द्रव्याचा मार्गण (हे द्रव्य ठिकठिकाणी कसे कसे जाते याचा उपकरणाद्वारे मागोवा घेण्याकरिता) म्हणून उपयोग करणे. रासायनिक रचनेचा अभ्यास, भूविज्ञान, अभियांत्रिकी वगैरेंच्या संशोधनासाठी यांचा उपयोग करता येतो. किरणोत्सर्गी समस्थानिक द्रव्ये रासायनिक विक्रियांमध्ये सहभागी होतात. या गुणधर्मावरच किरणोत्सर्गी समस्थानिकांचा मार्गण म्हणून होणारा उपयोग अवलंबून आहे.
(अ) जीवशास्त्रीय उपयोग : वनस्पती व प्राणी यांच्यामध्ये इष्ट परिणाम उत्पन्न करण्यासाठी किरणोत्सर्गाचा उपयोग करता येतो. विशेषत: वनस्पतीच्या बीजांच्या वृद्धीतील बदल त्यांच्या उत्परिवर्तनाच्या (आनुवंशिक बदलांचा अंतर्भाव होण्याच्या) वेगावर अवलंबून असतो. तांदूळ, गहू यांसारख्या अन्नधान्याच्या बीजांवर असे प्रयोग (उदा., γ किरणांची मर्यादित मात्रा देणे) यशस्वी झाले आहेत असे दिसते. भाजीपाल्याची वाढही या उपायाने पुष्कळ वाढवता येते हे प्रयोगाने दिसून आले आहे. शेतातील हानिकारक कीटकांचा किंवा त्यांच्या बीजांचा नाशही किरणांच्या भडिमाराने होऊ शकतो. याशिवाय रासायनिक खतांचे शोषण वनस्पतीमध्ये कसकसे होते, जमिनीचा ओलावा किती खोलपर्यंत आहे, प्रकाश संश्लेषण (प्रकाशीय ऊर्जेचे कार्बन डाय-ऑक्साइड व पाणी यांच्यापासून कार्बोहायड्रेटे तयार होणे) कसे होते इत्यादींसंबंधीची माहिती मार्गण द्रव्यांच्या साहाय्याने मिळते.
(आ) वैद्यकीय उपयोग : रोगाचे निदान करणे व रोगग्रस्त कोशिका नष्ट करणे असा दुहेरी उपयोग किरणोत्सर्गी समस्थानिकाने करता येतो. काही समस्थानिक द्रव्ये शरीरातील विशिष्ट कोशिकांमध्ये शोषली जातात आणि तेथे त्यांचा साठा होतो. अर्थात त्या भागातच त्यांचा परिणाम होतो. अवटू (श्वासनालाच्या दोन्ही बाजूस असलेल्या, थायरॉइड) ग्रंथींची जास्त वाढ आयोडीन (१३१) हा समस्थानिक वापरून कमी करता येते. सुवर्ण (१९८) या समस्थानिकाचा उपयोग गुल्म (शरीरक्रियेस निरुपयोगी असलेल्या गाठीच्या) निर्मूलनाकरिता होतो. कर्करोगाच्या घातकी कोशिका काही ठराविक मात्रा देऊन (क्ष किंवा β किरण) नष्ट करता येतात. मात्र शरीराच्या पृष्ठभागी हा रोग असेल तरच हे साध्य होते, शरीराच्या अंतर्भागामध्ये ही पद्धत वापरता येत नाही. पांडुरोगावर (ॲनिमियावर) किरणोत्सर्गी फॉस्फरसचा उपयोग होतो. हे शास्त्र अद्यापि पूर्णत्वास गेलेले नाही.
(इ) औद्योगिक क्षेत्रातील उपयोग : कापड, कागद, धातुपटल, प्लॅस्टिक, रबर वगैरे पदार्थांच्या तक्त्यांची किंवा पट्ट्यांची जाडी मोजणे आणि उत्पादनामध्ये ती विशिष्ट मर्यादेमध्ये कायम राखणे हे कार्य किरणोत्सर्गी द्रव्यांच्या साहाय्याने अचूक साधता येते. रबराच्या कारखान्यात रबराचा पातळ पट्टा किंवा कागदाच्या कारखान्यातील कागद एका गोल दंडावर गुंडाळला जातो, त्याची जाडी ठराविक असते. पट्ट्याच्या खाली सोईस्कर असे α, β किंवा γ किरणोत्सर्गी द्रव्य असते. पट्ट्याच्या विशिष्ट जाडीमध्ये शोषण होऊन पार जाणाऱ्या किरणांची तीव्रता किती असली पाहिजे हे आधी निश्चित करता येते. बाहेर पडणारे किरण गायगर गणित्राने किंवा प्रकाशविद्युत् घटामध्ये (प्रकाश पडल्याने ज्याच्या विद्युत् स्थितीत बदल होतो अशा प्रयुक्तीमध्ये) उत्पन्न होणाऱ्या विद्युत् स्पंदाच्या (अल्प कालीन तरंगाच्या) गणनाने मोजता येतात. यावरून जाडी सारखी राहिली की नाही एवढेच नव्हे तर या गणित्राच्या साहाय्याने जाडी नियंत्रण करणाऱ्या उपकरणाचे आपोआप नियंत्रणही करता येते. हेच तंत्र रंगाचे थर, छापखान्यातील छपाईच्या शाईची जाडी, शुद्ध धातूच्या पटलाची जाडी इत्यादींचे अचूक नियंत्रण करण्याकरिता वापरता येते. छपाईच्या शाईमध्ये फॉस्फरस (३२) पेंटाक्लोराइड हे मार्गण द्रव्य वापरून शाईमधून निघणाऱ्या कणांच्या साहाय्याने छपाईमध्ये किती शाई वापरली जाते ते पाहता येते. प्लॅस्टीकमध्ये ठराविक रासायनिक द्रव्याचे कसे विसरण होते हे किरणोत्सर्गी फॉस्फरस (३२) वापरून पाहता येते. पोलादाच्या भट्टीमध्ये जो दगडी कोळसा वापरतात त्यामध्ये नको असलेला गंधक असतो. दोन प्रकारच्या गंधकातील कोणता प्रकार या कोळशामध्ये जातो याचा अभ्यास करणे आवश्यक असते. सल्फर (३५) हा समस्थानिक वापरून कृत्रिम पायराइड कोळशामध्ये मिसळून हा भट्टीमध्ये जाळल्यानंतर उत्पन्न होणाऱ्या वायूमध्ये तो कोठे जातो याचा शोध घेता येतो. अनेक यंत्रांमधील गतिमान भागांमधील घर्षण आणि झीज यांच्या अभ्यासासाठी किरणोत्सर्गी मार्गणाचा फार उपयोग झाला आहे. वंगण द्रव्यांचे कार्य कसे होते, याचाही अभ्यास त्याने करता आलेला आहे. धातूचे ओतकाम किंवा जोडकाम व्यवस्थित झाले आहे की नाही हे क्ष-किरण किंवा गॅमा किरणांच्या छायाचित्रणाने निश्चित करता येते. विमानांतील धातूंचे भाग, बाष्पित्रे (बॉयलर) आणि मोठे नळ इत्यादींच्या परीक्षणाकरिता ही पद्धत आता प्रमाण ठरली आहे. अनेक औद्योगिक क्रियांमध्ये मार्गण द्रव्यांचा उपयोग होतो. किंबहुना अनेक प्रश्न मार्गण द्रव्यांच्या तंत्राने सोडवता येतील आणि त्याकरिता लागणारी रचना साधता येईल असे म्हटले तर वावगे होणार नाही.
(ई) कालनिर्णयाकरिता कार्बन (१४) या समस्थानिकाचा उपयोग : नायट्रोजनावर विश्वकिरणातील न्यूट्रॉनांच्या होणाऱ्या आघातांमुळे किरणोत्सर्गी कार्बन (१४) निर्माण होतो.
7N14 + 0n1 → 6C14 + 1H1 + 0.61 Mev ऊर्जा
6C14 → 7N14 (स्थिर) + β– कण + 0.16 Mev ऊर्जा
कार्बन (१४) चे अर्धायुष्य ५,५७० ± ४० वर्षे आहे आणि माध्य आयुष्य ८,००० वर्षांचे आहे. सु. २० अर्ध्यायुष्याच्या कालात म्हणजे सु. १,००,००० वर्षांत वातावरणामध्ये कार्बन (१४) चा समतोल निर्माण होतो. म्हणजे कोणत्याही कालात जेवढे कार्बन (१४) चे द्रव्यमान निर्माण होते तेवढेच त्या कालात त्याच्या ऱ्हासामुळे नष्टही होते. वातावरणातील कार्बनाबरोबर या उत्पन्न झालेल्या कार्बन (१४) चे प्रमाण प्रत्येक ग्रॅमला ७ मायक्रोमायक्रो क्यूरी कार्यप्रवणता असणारे द्रव्यमान इतके असते. आता कार्बन (१४) लाकूड किंवा खडक यांमध्ये बंदिस्त झाला तर हे प्रमाण त्याच्या ऱ्हासामुळे ५,५७० वर्षे या अर्धायुष्याला अनुसरून कमी होत जाईल. कार्बन (१४) च्या उपयोगाने कालमापन करण्याच्या पद्धतीचे हे तत्त्व आहे. अचूक कालमापनाकरिता मापन करण्याचा काल ५,५७० वर्षे याच्या मानाने फार मोठा किंवा फार लहानही असता कामा नये. या पद्धतीने जुने खडक किंवा लाकूड याचा काल सु. १० – १५ हजार वर्षे किंवा फारतर ४० – ५० हजार वर्षांपर्यंत मोजण्याची शक्यता आहे. ही पद्धत डब्ल्यू. एफ्. लिबी यांनी बसविली आणि असा निश्चित केलेला काल इतर भूवैज्ञानिक पद्धतींनी जुळता येतो असे आढळले आहे [→ किरणोत्सर्गी कार्बन कालनिर्णय पद्धति].
(उ) इतर उपयोग : रासायनिक विक्रियांवरील नियंत्रण आणि त्यांचे पृथ:क्करण यांकरिताही किरणोत्सर्गी मार्गण द्रव्यांचा उपयोग होतो. रासायनिक संयुगाची रचना कशी आहे तेही या तंत्राने अभ्यासिता येते. गोदामातील धान्य उत्तम स्थितीत राखणे, दूध, मांस हे पदार्थ टिकविणे, ऐतिहासिक कालीन विषप्रयोगाविषयक पुरावा वगैरे नाना प्रश्न मार्गण द्रव्यांनी सोडविता येतात.
पहा : अणुऊर्जेचे शांततामय उपयोग; प्रारण जीवविज्ञान; समस्थानिक.
संदर्भ : 1. Evans, R. D. The Atomic Nucleus, New York, 1965.
2. Lapp, R. E.; Andrewa, H. L. Nuclear Radiations Physics, 1954.
3. Segre, E. Nuclei and Particles, New York, 1964.
4. Semat, H. Introduction to Atomic and Nuclear Physics, New York, 1962.
5. The Publications Division, Government of India, Nuclear Explosions and their Effects, New Delhi, 1958.
बापट, अ. वा.