कालश्रेढी विश्लेषण : स्थूलमानाने एखाद्या चलाच्या ( बदलत्या राशीच्या) मूल्यांचा कालक्रमानुसार अनुक्रम लावला, तर त्याला कालश्रेढी म्हणतात. स्वाभाविकच, अशा कालश्रेढीच्या अभ्यासामध्ये कालमान हे स्वयंचल ( स्वत: बदलणारा चल) आणि अभ्यास करावयाचा चल तो परचल (स्वयंचलाच्या मूल्यांनुसार बदलणारा चल) मानून त्यांचा अन्योन्य संबंध अजमाविणे हे उद्दिष्ट असते. अशा अभ्यासामुळे त्या विशिष्ट चलाचे स्वरूप कळण्यास मदत तर होतेच, पण शिवाय दोन कालश्रेढींच्या अभ्यासावरून दोन निरनिराळ्या चलांच्या परस्परसंबंधावर व कार्यकारणभावांवरही प्रकाश पडू शकतो.
सांख्यिकीच्या अनेक शाखांमध्ये एखाद्या चलाच्या निरीक्षित मूल्यांचा ज्यावेळी अभ्यास करण्यात येतो ( उदा., प्रतिदर्शावरून म्हणजे चलाच्या मूल्यांच्या नमुन्यावरून समष्टीबद्दल म्हणजे चलाच्या मूल्यांच्या समग्र समुदायाबद्दल अनुमाने काढण्याकरिता) त्यावेळी बहुधा या निरीक्षणांचा कालानुसार काही अनुक्रम नसतो किंवा असला तरी त्याला विशेष महत्त्व नसते. परंतु काही परिस्थितींत या निरीक्षणांचा कालानुसार अनुक्रम लावणे शक्य असते आणि तो तसा लावला, तर त्यावरून त्या चलाचे स्वरूप समजण्यास मदत होऊन त्यापासून विशिष्ट प्रकारची योग्य ती अनुमाने काढणे शक्य होते. उदा., एखाद्या शहरातील निरनिराळ्या पंचवीस दुग्धालयांतील एखाद्या विशिष्ट दिवशी असलेले भाव नोंदले, तर त्यांवरून त्या शहरातील दुधाच्या सरासरी भावाची व त्या भावांच्या अपस्करणाची (बदलाच्या मर्यादांची) कल्पना येईल. या पाहणीमध्ये घेतलेल्या निरीक्षणांचा कालानुसार काही क्रम नसतो आणि ही निरीक्षणे कोणत्याही क्रमाने विचारात घेतली तरी चालतात. याउलट समजा, त्याच शहरातील दुधाचा सरासरी भाव पंचवीस आठवडे नोंदला आणि त्यांचा अभ्यास केला, तर त्या भावातील कालानुसार होणाऱ्या चढउतारावरून बरीच उपयुक्त अनुमाने काढता येतील. एखाद्या रोग्याच्या शरीराचे तपमान दर तासानंतर नोंदल्यास, त्या तपमानातील कालमानानुसार होणाऱ्या फेरबदलांच्या अभ्यासावरून रोगाचे निदान करण्यास व त्यावर करण्यात येणाऱ्या उपचारांचा परिणाम अजमावण्यास मदत होईल. वरील दोन्ही उदाहरणांत नोंदलेल्या निरीक्षणांचा कालानुसार असलेला क्रम बदलून चालणार नाही. विशेषत: अर्थशास्त्रीय व व्यापारविषयक प्रश्न्नांमध्ये एखाद्या चलाच्या कालक्रमानुसार होणाऱ्या बदलांना वा चढउतारांना फारच अर्थ व महत्त्व असणे शक्य असते आणि त्यांच्या अभ्यासामुळे बऱ्याच उपयुक्त बाबींवर प्रकाश पडू शकतो.
कालश्रेढीचे प्रमुख घटक : स्थूलमानाने पाहता असे दिसून येते की, प्रत्येक कालश्रेढीमध्ये तीन–चार वेगवेगळ्या प्रकारचे घटक एकाच वेळी उपस्थित असतात. या घटकांचे स्वरूप निरनिराळे असते आणि ते स्थूलमानाने एकमेकांपासून स्वतंत्र असतात. अभ्यास करावयाच्या चलाचे एखाद्या विशिष्ट काळचे निरीक्षित मूल्य हे या घटकांच्या एकमेकांवरील अध्यारोपणातून निष्पन्न झालेले असते, असे मानावयास हरकत नाही. हे अध्यारोपण योगशील (घटकांची बेरीज करता येण्यासारखे) किंवा गुणनक्षम (घटकांचा गुणाकार करता येण्याजोगे ) असू शकते. बहुतेक कालश्रेढींमध्ये पुढील घटक आढळतात. (१) दीर्घकालीन प्रवृत्ती : यात चलाच्या मूल्यातील तात्कालिक स्वरूपाच्या फेरबदलांचा विचार न करता ठोकळमानाने दीर्घ मुदतीवर पसरलेल्या चढउतारांचा अंतर्भाव होतो. (२) हंगामी चढउतार : यात ऋतुमानाप्रमाणे कमी जास्त होणाऱ्या आणि म्हणूनच एक वर्ष किंवा कमी आवर्तकाल ( एका चढउतारास लागणारा काल ) असलेल्या नियतकालिक फेरबदलांचा समावेश होतो. (३) चक्रीय चढउतार : यात वर्षापेक्षा जास्त आवर्तकाल असलेल्या नियतकालिक चढउतारांचा अंतर्भाव होतो. (४) अनियमित चढउतार : यात तात्कालिक आणि यद्दच्छ स्वरूपाच्या फेरबदलांचा समावेश होतो.
खालील कोष्टकामध्ये एका चलाचे प्रत्येक वर्षाला आढळणारे प्रत्यक्ष मूल्य स्तंभ (५) मध्ये दाखविले आहे. हे मूल्य (अ) स्तंभ (२) मध्ये दाखविलेल्या य = ½ क्ष२ + ½ क्ष –१ या सूत्राने दिलेल्या अन्वस्तीय (पॅराबोलिक) दीर्घकालीन प्रवृत्तीनुसार होणारे मूल्य, (आ) स्तंभ (३) मध्ये दाखविलेल्या पाच वर्षांचा आवर्तकाल असलेल्या
| वर्ष | दीर्घकालीन प्रवृत्ती | चक्रीय फेरबदल | अनियमित फेरबदल | एकूण प्रत्यक्ष मूल्य |
| १ | २ | ३ | ४ | ५ |
| १ | ० | +३ | –१ | २ |
| २ | २ | +१ | +२ | ५ |
| ३ | ५ | ० | +१ | ६ |
| ४ | ९ | –१ | ० | ८ |
| ५ | १४ | –३ | –२ | ९ |
| ६ | २० | +३ | +१ | २४ |
| ७ | २७ | +१ | +१ | २९ |
| ८ | ३५ | ० | –३ | ३२ |
| ९ | ४४ | –१ | ० | ४३ |
| १० | ५४ | –३ | –१ | ५० |
| ११ | ६५ | +३ | +२ | ७० |
| १२ | ७७ | +१ | +१ | ७९ |
| १३ | ९० | ० | –१ | ८९ |
| १४ | १०४ | –१ | –२ | १०१ |
| १५ | ११९ | –३ | +१ | ११७ |
| १६ | १३५ | +३ | +१ | १३९ |
चक्रीय चढउताराचे मूल्य आणि (इ) स्तंभ (४) मध्ये दाखविलेले अनियमित स्वरूपाचे फेरबदल यांच्या अध्यारोपणातून मिळालेले आहे. या कालश्रेढीमध्ये कालमानाचे एकक वर्ष असल्यामुळे यात ऋतुमानानुसार होणाऱ्या हंगामी फेरबदलांचा समावेश नाही. कालश्रेढीच्या वर दिलेल्या घटकांपैकी पहिल्या तीन घटकांची पुढील आकृत्यांवरून चांगली कल्पना येईल.
कालश्रेढीच्या चार प्रकारच्या घटकांचा विस्तारश: विचार खाली केला आहे.
दीर्घकालीन प्रवृत्ती : बऱ्याच कालश्रेढींमध्ये असे आढळते की, त्यांतील मूल्ये ( अल्पकालीन व किरकोळ स्वरूपाचे फेरबदल विचारात न घेतल्यास ) स्थूलमानाने एखाद्या विशिष्ट सूत्रानुसार वाढत किंवा कमी होत जातात. ही वाढ किंवा घट दीर्घकालपर्यंत पसरलेली असते. उदा., भारतातील गेल्या पन्नास वर्षांतील साक्षरतेचे प्रमाण वाढत चाललेले आढळते, तर बालमृत्यूंचे प्रमाण कमी होत गेलेले दिसते. चलाचे एखाद्या वेळचे प्रत्यक्ष मूल्य या दीर्घकालीन प्रवृत्तीनुसार अनुमान केलेल्या मूल्याच्या जवळपास असल्याने या प्रवृत्तीचे स्वरूप ठरविणे व जमल्यास ती सूत्रबद्ध करणे जरुरीचे व हितावह असते. हे स्वरूप अनेक प्रकारचे असू शकते. त्यांतील काही प्रकार पुढीलप्रमाणे ( येथे कालमान क्ष ह्या अक्षराने आणि त्यानुसार बदलणाऱ्या चलाचे मूल्य य ह्या अक्षराने दर्शविले आहे).
(अ) रैखिक :य = क + खक्ष ( येथे क आणि ख हे स्थिरांक आहेत). हे क्ष आणि य या चलांमधील अन्योन्य संबंधाचे सर्वांत
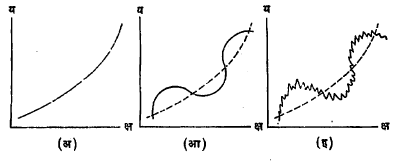 साधे संभाव्य स्वरूप आहे. ज्यावेळी क्ष च्या प्रत्येक एकक वाढीबरोबर (उदा., दर वर्षाला) य मध्ये ख या निश्चित मूल्याने वाढ होते त्यावेळी रैखिक कालश्रेढी संभवते.
साधे संभाव्य स्वरूप आहे. ज्यावेळी क्ष च्या प्रत्येक एकक वाढीबरोबर (उदा., दर वर्षाला) य मध्ये ख या निश्चित मूल्याने वाढ होते त्यावेळी रैखिक कालश्रेढी संभवते.
(आ) अन्वस्तीय :य = क + खक्ष + गक्ष२ किंवा य = क + खक्ष + गक्ष२ + . . . . + मक्षप . ज्यावेळी रैखिक सूत्र एखाद्या कालश्रेढीशी समाधानकारकपणे जुळत नाही, त्यावेळी वरीलसारख्या पदावलीतील योग्य तितकी पदे घेऊन कालश्रेढीची दीर्घकालीन प्रवृत्ती अजमावता येते. एखाद्या विशिष्ट कालश्रेढीसाठी किती पदे घेणे योग्य होईल हे ठरविण्याच्या पद्धतीही उपलब्ध आहेत. वर दिलेल्या कोष्टकातील कालश्रेढीमध्ये स्तंभ (२) मधील मूल्ये य = १/२क्ष२ + १/२ क्ष –१ या सूत्रानुसार आहेत.
(इ) घातीय : य = क.खक्ष या स्वरूपाचे. ज्यावेळी चलाच्या वाढीचा दर हा चलाच्या प्रमाणात असतो त्यावेळी अशा प्रकारची कालश्रेढी संभवते. उदा., एखाद्या देशाचे राष्ट्रीय उत्पन्न दरवर्षी त्या उत्पन्नाच्या प्रमाणातच ( उदा., ५ टक्के) वाढत असेल, तर त्या राष्ट्रीय उत्पन्नाची वाढ वरील प्रकारची असेल. अर्थात या स्वरूपात लॉग य आणि क्ष यांचा परस्परसंबंध रैखिक असेल.
(ई) वृद्धी वक्र आणि गॉम्पर्ट्स वक्र : यांची सूत्रे अनुक्रमे १/य = क + ख. घक्ष आणि लॉग य = क + ख.घक्ष अशी दिली जातात. अशा प्रकारची सूत्रे काही विशिष्ट वर्धिष्णू चलांना (उदा., एखादा उद्योगधंदा, लोकसंख्या) लागू पडतात.
एखाद्या कालश्रेढीच्या दीर्घकालीन प्रवृत्तीचे स्वरूप ठरविण्याच्या बऱ्याच पद्धती आहेत. त्यांपैकी काही पुढीलप्रमाणे आहेत.
(१) मुक्तहस्ताकृती किंवा निरीक्षणद्वारा आलेखन : या पद्धतीत कालमान हे स्वयंचल क्ष अक्षावर आणि परचल य अक्षावर दाखवून नेहमीच्या रीतीने बिंदूंची स्थापना केली जाते. अशा रीतीने मिळालेल्या बिंदू संचाच्या शक्यतो मधोमध जाणारा सफाईदार वक्र निरीक्षणाने काढला जातो. असे वक्र काढणाऱ्याच्या अनुभवावर आणि कौशल्यावर अवलंबून असल्यामुळे त्यांत अनिश्चितता येते. या पद्धतीने कालश्रेढीच्या प्रवृत्तीचा नुसता आलेख मिळतो, त्याचे सूत्र मिळत नाही. ह्या दोषामुळे ही पद्धती तितकीशी ग्राह्य नाही. तथापि फारशी गणनक्रिया न करता कालश्रेढीचे स्वरूप अल्पकाळात समजण्यास या पद्धतीची मदत होते
(२) लघुतम वर्ग पद्धती : या पद्धतीत कालमान (क्ष) आणि परचल (य) यांच्यामध्ये एखाद्या निश्चित स्वरूपाचा अन्योन्य संबंध गृहीत धरून त्यात येणाऱ्या प्रचलांची (विशिष्ट परिस्थितीत स्थिर राहणाऱ्या राशींची) मूल्ये काढली जातात. ही मूल्ये काढताना श्रेढीतील वेगवेगळी (प्रत्यक्ष) मूल्ये व गृहीत सूत्रानुसार येणारी ती ती अपेक्षित मूल्ये यांच्या फरकांच्या वर्गांची बेरीज लघुतम केली जाते. म्हणजेच कालश्रेढीतील चलाची य१, य२, य३, . . . ., यप ही प्रत्यक्ष मूल्ये असतील व गृहीत सूत्रानुसार ज१, ज२, ज३, . . . , जप ही संगत अपेक्षित मूल्ये असतील, तर त्या सूत्रातील प्रचलांची मूल्ये ( य१– ज१ )२ + ( य२ – ज२ )२ + . .. . . + ( यप –जप )२ ही राशी लघुतम होईल याप्रमाणे काढली जातात. कालश्रेढीची प्रवृत्ती रैखिक वा अन्वस्तीय असेल तर ती या पद्धतीने काढता येते. इतर प्रकारची असली तरीही बहुधा थोड्याफार फरकाने (उदा., य चा किंवा क्ष चा किंवा दोहोंचाही लॉगरिथम घेऊन) ही पद्धती वापरता येते. लघुतम केलेल्या वरील राशीचे मूल्य जेवढे कमी होईल तेवढ्या प्रमाणात दिलेल्या कालश्रेढीकरिता गृहीत धरलेले सूत्र योग्य आहे असे म्हणण्यास हरकत नाही.
(३) गतिमान सरासरी पद्धती : या पद्धतीमध्ये चक्रीय, स्वल्पकालीन व अनियमित घटकांचा योग्य त्या मुदतीची सरासरी घेऊन निरास करण्याचा प्रयत्न केला जातो. त्यासाठी आधी चक्रीय फेरबदलाचा आवर्तकाल अजमावा लागतो व त्याकरिता वेगळ्या पद्धती उपलब्ध आहेत. समजा, कालमानाचे एकक वर्ष आहे आणि श्रेढीचा आवर्तकाल ५ वर्षे आहे, तर चलाच्या पहिल्या ते पाचव्या वर्षाच्या मूल्यांची सरासरी तिसऱ्या ( म्हणजे केंद्रीय) वर्षी, दुसऱ्या ते सहाव्या वर्षाच्या मूल्यांची सरासरी चौथ्या वर्षी, तिसऱ्या ते सातव्या वर्षाच्या मूल्यांची सरासरी पाचव्या वर्षी याप्रमाणे सरासरी मांडल्या जातात आणि अशा सरासरी काढून आलेली मूल्ये त्या चलाची दीर्घकालीन प्रवृत्ती दर्शवितात, असे मानले जाते. ही स्वल्पकालीन व अनियमित फेरबदलांचा निरास करणारी व कालश्रेढीला सफाईदार वक्ररूप देणारी सोपी व सरळ रीत आहे. साधी सरासरी घेण्याऐवजी योग्य ती भारित सरासरी ( चलाच्या मूल्यांच्या महत्त्वानुसार त्यांना योग्य असे भार जोडून घेण्यात येणारी सरासरी ) घेण्याचीही पद्धत आहे. तसेच आवर्तकाल समसंख्या असेल, तर त्यानुसार काढलेली सरासरी केंद्रस्थ करण्यासाठी अशा दोन दोन सरासरींची पुन्हा सरासरी काढली जाते. जितक्या अनुगामी मूल्यांची सरासरी घेतली जाते, त्या संख्येला त्या गतिमान सरासरीची लांबी म्हणतात.
ही पद्धती वर दिलेल्या कोष्टकातील कालश्रेढीतील प्रत्यक्ष मूल्यांना लावल्यास ( पंचवार्षिक गतिमान सरासरी घेऊन) तिसऱ्या ते चौदाव्या वर्षांची मूल्ये ६, १०, १५, २०, २७, ३६, ४५, ५५, ६६, ७८, ९१, १०५ अशी आढळतील आणि ती त्याच कोष्टकातील स्तंभ (२) मधील त्या त्या वर्षाच्या मूल्यांशी उत्तम रीतीने जुळणारी आहेत.
ही पद्धती वर दिलेल्या रैखिक किंवा अन्वस्तीय दीर्घकालीन प्रवृत्ती कालश्रेढीला अन्वायोजित करण्याच्या (एखाद्या गणितीय वक्राची दिलेल्या सांख्यिकीय आकडेवारीला अनुरूप जुळणी करण्याच्या) पद्धतीसारखीच आहे. फरक इतकाच की, ही प्रवृत्ती या पद्धतीत सबंध श्रेढीला अन्वायोजित न करता श्रेढीच्या काही विशिष्ट लांबीच्या भागाला अन्वायोजित करण्यात येते आणि त्यावरून त्या त्या भागाच्या मध्यबिंदूस योग्य असे मूल्य काढले जाते. ही अन्वायोजित प्रवृत्ती रैखिक नसल्यास साध्या सरासरीऐवजी भारित सरासरी घ्यावी लागते. अशा सरासरीमध्ये वापरावयाचे भार निवडलेल्या अन्वस्ताच्या घातावर व सरासरीच्या लांबीवर अवलंबून असतात.
गतिमान सरासरी पद्धतीमधील एक दोष असा की, अशा सरासरीची लांबी ल असल्यास सरासरी काढून मिळालेली श्रेढी मूळ श्रेढीपेक्षा ल –१ मूल्यांनी लहान असते. म्हणून मूळ कालश्रेढीच लहान असल्यास ही पद्धती वापरणे योग्य होणार नाही. तसेच या पद्धतीचा कालश्रेढीतील भविष्यकालीन मूल्ये अजमाविण्यासाठीही उपयोग होत नाही. याकरिता वर दिलेली लघुतम वर्ग पद्धती जास्त सरस ठरते. तसेच गतिमान सरासरी घेऊन मिळालेल्या श्रेढीमध्ये मूळ श्रेढीत नसलेले चक्रीय चढउतार शिरल्याचे पुष्कळदा आढळते. यालाच स्लट्झ्की–यूल परिणाम ( स्लट्झ्की व यूल यांनी स्वतंत्रपणे अभ्यासल्यामुळे दोघांच्या संयुक्त नावाने ओळखण्यात येणारा परिणाम ) म्हणतात. हे सर्व दोष असूनही गतिमान सरासरी पद्धती तिच्या सरलपणामुळे फार उपयुक्त ठरली आहे.
हंगामी ( किंवा ऋतुवार) चढउतार : एखाद्या वस्तूच्या किंमती, उत्पादन, विक्री वगैरेंमध्ये ऋतुमानानुसार फेरबदल होत असतात. उदा., पेरणी जवळ आली म्हणजे धान्यांच्या किंमती वाढतात आणि नवे पीक हाती येऊन पुरवठा वाढल्याबरोबर किंमती उतरतात. तसेच दसरा–दिवाळीसारख्या उत्सवप्रसंगी किंवा लग्नाच्या मोसमात कापड, दागदागिने यांची विक्री वाढते. अशा विशिष्टकालीन फेरबदलांना हंगामी चढउतार म्हणतात आणि ते साप्ताहिक किंवा मासिक आकडेवारी गोळा केलेल्या कालश्रेढीमध्ये स्पष्ट दिसून येतात. अर्थात हे चढउतार दीर्घकालीन चढउतारांहून वेगळे आणि स्वतंत्र असून त्यांच्यावर अध्यारोपित असतात.
समजा, एका कारखान्याच्या विक्रीची १९५१ – ६० या दहा वर्षांची मासिक आकडेवारी उपलब्ध आहे आणि तीतील मासिक फेरबदलांचा अभ्यास करावयाचा आहे. यासाठी एक पद्धत म्हणजे जानेवारी, फेब्रुवारी, . . . . . अशी मासवार (दहा वर्षांची) सरासरी काढली जाते. उदा., दहाही वर्षांतील जानेवारीच्या आकड्यांची सरासरी काढल्यास ती जानेवारीची सरासरी होईल. नंतर या बारा मासवार सरासरींची अंतिम सरासरी काढली जाते. ही सरासरी १०० कल्पून प्रत्येक मासिक सरासरीचा निर्देशांक काढला जातो. उदा.,
| जानेवारीचा निर्देशांक = | जानेवारीची सरासरी | X १००· |
| अंतिम सरासरी |
असे बारा निर्देशांक मिळाल्यावर त्यांवरून त्या विक्रीच्या मासानुसार होणाऱ्या फेरबदलांची चांगली कल्पना येऊ शकते.
मासिक फेरबदलांचा अभ्यास करण्याची आणखी एक पद्धत म्हणजे दिलेल्या श्रेढीच्या आकडेवारीतून आधी दीर्घकालीन प्रवृत्तींचा गतिमान सरासरी ( किंवा इतर) पद्धतीने निरास करून राहिलेल्या घटकांची मासवार सरासरी काढणे. उदा., समजा, वरील उदाहरणात दहा वर्षांतील जानेवारीचे प्रत्यक्ष आकडे (टनांत) १८२, १६७, १९३, २१५, २५६, ३१५, ३३५, ३४२ व ३३६ असे आहेत आणि द्वादशमासिक (जानेवारी केंद्रित) गतिमान सरासरीने आलेले आकडे २२५, १९५, २०६, २६३, २९८, ३३५, ३५५, ३७६ व ३७८ असे आहेत. हे आकडे वजा जाता बाकी –४३,–२८, –१३, –४८, –४२, –२०, –२०, –४१,–३४,–४२ असे आकडे येतात. यांची सरासरी–३३ येते. हे विक्रीवरील जानेवारी –विशिष्ट हंगामी परिणामाचे मूल्यमापन होय. स्थूलमानाने याचा अर्थ असा की, विक्रीचा आकडा एखाद्या वर्षाच्या जानेवारीत दीर्घकालीन प्रवृत्तीनुसार जेवढा यावयास पाहिजे त्यापेक्षा तो सु. ३३ या संख्येने कमी येईल. याचप्रमाणे इतर महिन्यांचे मासविशिष्ट घटक काढता येतील. मासवार फेरबदलाऐवजी साप्ताहिक किंवा त्रैमासिक स्वरूपाचे नियतकालिक फेरबदल ( योग्य त्या कालश्रेढीमध्ये) अभ्यासण्याचीही पद्धती आहे.
चक्रीय चढउतार : वर्षानुवर्षे अवधीची ज्यांची आकडेवारी उपलब्ध आहे अशा बऱ्याचशा चलांमध्ये असे आढळून येते की, त्यांत दीर्घकालीन चढउतारांशिवाय काही विशिष्ट वर्षांचा आवर्तकाल असलेला चक्रीय घटक उपस्थित असतो. नियमितपणे येणाऱ्या तेजी आणि मंदीच्या लाटा असलेली व्यापारचक्रे हे अशा चक्रीय चढउतारांचे उत्तम उदाहरण आहे. अर्थात अर्थशास्त्रीय कालश्रेढींमध्ये अशा चक्रांचे अस्तित्व व त्यांचा नियमितपणा नेहमीच जरूर तितका स्पष्ट आढळत नाही. कारण अशा श्रेढींची आकडेवारी इष्ट तेवढ्या लांब मुदतीकरिता गोळा केलेली नेहमीच उपलब्ध असेल असे नाही आणि त्यांचा परिणाम पूर, दुष्काळ, लढाया, तांत्रिक, सुधारणा वगैरे कारणांमुळे पुष्कळदा झाकला जातो. एखाद्या पन्नास वर्षांच्या श्रेढीत आढळलेली दीर्घकालीन वर्धिष्णू (किंवा इतर) प्रवृत्ती ही वस्तुत: १०० किंवा २०० वर्षे आवर्तकाल असलेल्या चक्रीय चढउताराचा भाग असणे शक्य असते आणि म्हणून ती प्रवृत्ती तशीच पुढे चालू राहील असे अनुमान काढणे धोक्याचे असते.
अशा चक्रीय चढउतारांची छाननी करण्यासाठी कालश्रेढीतील इतर घटकांचा निरास करावा लागतो. एखाद्या कालश्रेढीमध्ये एकापेक्षा अधिक चक्रांचे अध्यारोपण किंवा त्यांचा समन्वय झालेला असणे शक्य असते किंवा चक्राचा आवर्तकाल निश्चित नसतो. या सर्व गोष्टींचा विचार करून चक्रांचा अभ्यास करावा लागतो. यासाठी मुख्यत्वे ‘आवर्तकाल – आलेख – विश्लेषण पद्धती’ चा उपयोग करतात.
जर मूळ कालश्रेढीमध्ये
| { | क x ज्या | ( | २pक्ष | ) | + ख x कोज्या | ( | २pक्ष | ) | } |
| ल | ल |
या स्वरूपाचे, म्हणजेच ल हा आवर्तकाल आणि Ö क२ + ख२ हा परमप्रसर (एखाद्या सरासरी मूल्यापासून शिखरावरील वा तळावरील जास्तीत जास्त दूरस्थ असणारे मूल्य) असलेले (एक किंवा अधिक) चक्रीय घटक असतील, तर असे ठळक प्रकारचे घटक आणि त्यांचे आवर्तकाल व परमप्रसर अजमावणे आवर्तकाल – आलेख – विश्लेषणाने शक्य होते.
अनियमित व यद्दच्छ फेरबदल : प्रत्येक कालश्रेढीमध्ये सूत्रबद्ध करण्याजोग्या नियमित वा चक्रीय घटकांशिवाय काही अनियमित व स्वल्पकालीन स्वरूपाचा भाग असतो. कारण एखाद्या वेळचे चलाचे मूल्य हे अनेक प्रकारच्या नियंत्रित – अनियंत्रित, अपेक्षित – अनपेक्षित कारणांच्या परिणामांतून बनलेले असते. उदा., एखाद्या पेठेतील मालाची विक्री किंवा एखाद्या कारखान्यातील मालाचे साप्ताहिक उत्पादन हे नित्य व हंगामी अशा काही कारणांशिवाय नैमित्तिक, तात्कालिक व अनिश्चित स्वरूपाच्या काही कारणांवरही अवलंबून असते व त्या प्रमाणात ते कमी जास्त होत असते. या प्रकारचे अनिश्चित फेरबदल एखाद्या कालश्रेढीच्या बाबतीत ठरविण्याची पद्धत म्हणजे वर उल्लेखिलेल्या पद्धतींनी दीर्घकालीन, चक्रीय व हंगामी फेरबदलांची छाननी करून ते प्रत्यक्ष मूल्यातून वजा करणे व शेष भाग अनियमित स्वरूपाचा समजणे, ही होय. उदा., वर दिलेल्या मासिक विक्रीच्या उदाहरणात दिलेल्या निरनिराळ्या जानेवारी महिन्यांच्या विक्रीच्या आकड्यांतून दीर्घकालीन प्रवृत्तीनुसार मिळालेले आकडे व जानेवारी मासविशिष्ट –३३ हा नियतकालीन आकडा वजा केला असता त्या त्या महिन्यातील –१०, + ५, +२०, –१५, –९, +१३, +१३,–८, –१ आणि –९ हे शेष घटक अनियमित स्वरूपाचे मानले जातील. याचा अर्थ असा की, ( उदा.,) जानेवारी १९५१ ची एकूण विक्री १८२ टन ही २२५ टन + (–३३ टन ) + ( –१० टन ) अशा घटकांची बनलेली आहे. असेच पृथक्करण त्या दहा वर्षांतील इतर सर्व महिन्यांतील आकड्यांचेही करता येईल. कालश्रेढीतील आकड्यांच्या अशा पृथक्करणालाच कालश्रेढी विश्लेषण म्हणतात.
अनियमित घटक व त्याचे विचरण (चलनशीलता दर्शविणारी एक राशी) काढण्याची ‘चर–अंतर पद्धती’ नावाची पद्धती टिंटनर यांनी दिली आहे. तिचे मुख्य तत्त्व स्थूलमानाने पुढीलप्रमाणे आहे: समजा, कालश्रेढीमध्ये क + खक्ष + गक्ष२ + . . . . मक्षप या स्वरूपाचा नियमित घटक आणि झ हा अनियमित घटकही आहे. अशा श्रेढीतील मूल्यांची ग१ = य२ – य१, ग२ = य३ – य२, . . . . अशी क्रमवार वजाबाकी व पुन्हा यांची घ१ = ग२ – ग१, घ२ = ग३– ग२, . . . अशी क्रमवार वजाबाकी व यांचीही पुन्हा तशीच क्रमवार वजाबाकी, असे क्रमवार करीत गेल्यास ज्या श्रेढी मिळत जातील त्यांत क्रमाने नियमित घटकाचा निरास होत जाईल, पण अनियमित घटक या पद्धतीने कमी होणार नाही. एवढेच नव्हे, तर वरीलप्रमाणे प +१ वेळा करून मिळालेल्या श्रेढीमध्ये नियमित घटकाचा पूर्ण निरास होऊन फक्त अनियमित घटक राहील. हे नक्की कोणत्या टप्प्यानंतर झाले आहे ते मिळालेल्या श्रेढींची विचरणे काढून आणि योग्य त्या कसोट्या लावून काढता येते व त्यावरून मूळ श्रेढीच्या नियमित घटकाचा घातांक, अनियमित घटक आणि त्याचे विचरण या गोष्टी काढता येतात.
दोन कालश्रेढींचे तुलनात्मक विश्लेषण : दोन कालश्रेढींच्या पृथक्करणावरून त्यांच्या अन्योन्य संबंधावर प्रकाश पडतो. अर्थात दोन चलांच्या सहसंबंधाचे स्वरूप कालश्रेढीच्या बाबतीत जरा वेगळ्या प्रकारचे असते. य आणि झ हे दोन चल जरी परस्पर संबद्ध असले, तरी त्यांच्या कालश्रेढीतील मूल्यांचा सहसंबंधांक (दोन चलांच्या एकमेकांवरील अवलंबित्वाचे मान दर्शविणारी राशी) ऋण स्वरूपाचा येऊ शकतो. याचे कारण असे की, झ हा य वर अवलंबून आणि य बरोबरच वाढणारा वा कमी होणारा असला, तरी य चा परिणाम झ वर जाणवेपर्यंत काही कालावधी लागतो. त्यामुळे य चे मूल्य वाढून त्यामुळे झ चे मूल्य वाढेपर्यंत य चे मूल्य पुन्हा कमी झालेले असते. परिणामी य चे मूल्य जास्त असेल त्यावेळी झ चे मूल्य कमी आणि य चे मूल्य कमी असेल त्यावेळी झ चे मूल्य जास्त अशी ऋण सहसंबंधांक दर्शविणारी परिस्थिती आढळून येते. म्हणून अशा चलांचा त्यांच्या कालश्रेढीवरून सहसंबंधांक काढताना त्यांच्या मूल्यांमध्ये योग्य तो कालावधी (म्हणजे विलंबकाल) सोडून मग काढावा लागतो. उदा., एखाद्या मालाचे उत्पादन य ह्याचा परिणाम त्याच्या किरकोळ विक्रीच्या किंमतीवर (झ वर) साधारण दोन वर्षांनंतर जाणवत असेल, तर य आणि झ यांच्यामधील परस्परसंबंधाचा अभ्यास करण्यासाठी वर्ष क मधील उत्पादन आणि वर्ष क + २ मधील किरकोळ विक्रीची किंमत यांच्यातील सहसंबंधांक काढणे योग्य होईल. हा विलंबकाल काढण्याच्या दोन मुख्य रीती आहेत. पहिली रीत म्हणजे निरनिराळ्या कालावधींचे विलंबकाल कल्पून सहसंबंधांक काढल्यावर जो उच्चतम सहसंबंधांक देईल, तो इष्ट विलंबकाल समजण्यात येतो. दुसरी रीत म्हणजे दोन्ही कालश्रेढी एकाच आलेखपत्रावर आलेखून त्यांच्या निकटच्या शिखरबिंदूंमधील कालावधी निरीक्षणाने अजमावून तोच विलंबकाल मानावयाचा.
अनुप्रयोग : कालश्रेढीच्या वर निर्देशिलेल्या पद्धतींनी केलेल्या अभ्यासाचा चलांच्या भविष्यकालीन संभाव्य मूल्यांचा अंदाज करण्यासाठी विशेष उपयोग होतो. उदा., एखाद्या देशाच्या लोकसंख्येची किंवा एखाद्या मालाच्या मागणीची वाढ पुढील दहा वर्षांत कशा स्वरूपाची होईल, याचा अंदाज त्या त्या चलाच्या मागील काही वर्षांतील वाढीच्या अभ्यासावरून करता येईल. असे अंदाज काढण्यासाठी कालश्रेढीचे विश्लेषण करून त्यातील घटकांचे स्वरूप ठरवावे लागते आणि इष्ट त्या भविष्यकालीन समयी लागू होणाऱ्या (अनियमित फेरबदल वगळून ) त्या घटकांची बेरीज करून त्यावेळचे अपेक्षित मूल्य काढावे लागते. तसेच झ या इष्ट चलाशी संलग्न असलेल्या दुसऱ्या एखाद्या य ह्या चलाची कालश्रेढीही उपलब्ध असेल आणि त्यांच्यातील विलंबकाल अजमावून काढलेला सहसंबंधांक ± १ च्या आसपास असेल, तर त्यांच्यामधील संबंध झ = क + ख य ह्या किंवा इतर तत्सम प्रकारचा कल्पून आणि य आणि झ यांमधील विलंबकाल लक्षात घेऊन य च्या योग्य त्या मूल्यावरून झ चे संभाव्य मूल्य अजमावता येते. या पद्धतीतील काही दोष असे: (१) य आणि झ यांच्यामधील परस्परसंबंध भूत व वर्तमानकाळी जे असतील, तेच भविष्यकाळी चालू राहतील असे नेहमीच गृहीत धरता येत नाही. कारण देशातील आर्थिक व्यवस्थेमधील फेरबदल, नवनवीन शोध, समाजातील बदलत्या चालीरीती व आवडीनिवडी इ. गोष्टींमुळे या संबंधात क्रांती वा विकास होत असतो. (२) वर उल्लेखिलेला सहसंबंधांक एखाददुसऱ्या चरम (दूरच्या ) मूल्यामुळे वाजवीपेक्षा कमी वा जास्त येऊन दिशाभूल होण्याचा संभव असतो. (३) विलंबकाल हा नेहमीच निश्चित असा नसतो. किंबहुना तो तेजीच्या वेळी एक आणि मंदीच्या वेळी दुसराच असणे शक्य असते. (४) झ चे भविष्यकालीन मूल्य अजमावताना य सारख्या संलग्न चलाचा उपयोग केला नाही तरी क्वचित असे घडते की, ( उदा.,) मागील काही वर्षांत आढळलेली झ ची वर्धिष्णू ( किंवा इतर ) प्रवृत्ती ही वर सुचविल्याप्रमाणे वस्तुत: दीर्घ आवर्तकाल असलेल्या चक्रीय चढउताराचा भाग असते आणि म्हणून ती प्रवृत्ती तशीच पुढे चालू राहील, असे गृहीत धरणे धार्ष्ट्याचे वा धोक्याचे असते.
असे काही दोष असले तरी कालश्रेढींच्या अभ्यासामुळे भविष्यकालीन परिस्थितीचा थोडाफार अंदाज येऊन व्यापारी, कारखानदार, सरकारी यंत्रणा वगैरेंना आपापल्या योजना, तंत्र, धोरणे इत्यादींबाबत योग्य ती आखणी व सुधारणा करणे शक्य होते असे म्हटल्यास अतिशयोक्ती होणार नाही. याच कारणांमुळे अशा अभ्यासाचा भारतामध्ये मोठ्या प्रमाणावर उपयोग करण्यात येत आहे. विशेषेकरून देशाच्या अर्थव्यवस्थेशी निगडित अशा विविध प्रकारच्या कालश्रेढींच्या हंगामी व दीर्घकालीन चढउतारांचा रिझर्व बॅंकेतर्फे अखंडपणे अभ्यास होत असून त्यावरून निघणारी आकडेवारी व निष्कर्ष नियमितपणे प्रसिद्ध केले जातात.
पहा : आर्थिक सांख्यिकी.
संदर्भ : 1.Croxton, F. E. Cowden, D.J. Applied General Statistics, Englewood Cliffs, N. J., 1955.
2. Croxton, F. E. Cowden, D.J. Practical Business Statistics, Englewood Cliffs, N.J., 1960.
3. Davis, H.T. The Analysis of Economic Time Series, Bloomington, Indiana, 1941.
4. Hannan, E. J. Time Series Analysis, New York, 1960.
5. Rao, K.S.Statistical Inference and Measurement of Structural Changes in an Economy, Bombay, 1964.
6. Umarji, R. K. Probability and Statistical Methods, Bombay, 1963.
नाडकर्णी, प्र. ना.
“