लाप्लास, प्येअर सीमाँ मार्कीद : (२३ मार्च १७४९-५ मार्च १८२७). फ्रेंच गणितज्ञ, ज्योतिर्विद व भौतिकीविज्ञ. सूर्यकुलाच्या स्थैर्यासंबंधी त्यांनी केलेले संशोधन कार्याबद्दल विशेष प्रसिद्ध. ज्योतिषशास्त्रातील त्यांच्या अनन्यसाधारण कामगिरीबद्दल त्यांना ‘फ्रेंच न्यूटन’ म्हणून कीर्ती मिळाली.
लाप्लास यांचा जन्म नॉर्मंडीतील बोमाँट-एन् ओझ येथे झाला. त्यांचे वडील थोडी संपदा असलेले एक यशस्वी शेतकरी होते. त्यांच्या प्रारंभीच्या आयुष्याबद्दल फारशी विश्वसनीय माहिती उपलब्ध नाही. कां विद्यापीठात धर्मशास्त्राचा अभ्यास करीत असताना गणितातील त्यांची बुद्धिमत्ता व उत्साह प्रकर्षाने दिसून आला. गणितातच कार्य करण्याचा निर्धार करून वयाच्या अठराव्या वर्षी ते पॅरिसला गेले. त्यांनी तत्कालिन प्रसिद्ध गणितज्ञ झां द ॲलांबेर यांना ⇨यामिकीच्या सर्वसाधारण तत्त्वांविषयी एक पत्र पाठविले. त्यामुळे प्रभावित होऊन ॲलांबेर यांनी थोड्याच काळात एकोल मिलितेर या संस्थेतील गणिताच्या प्राध्यापकपदासाठी लाप्लास यांची शिफारस केली.
त्यानंतर लवकरच लाप्लास यांनी कोणत्याही ⇨निर्धारक त्याच्या एकाद्या निवडलेल्या पंक्तीतील सर्व तयार होऊ शकणाऱ्या लघुकांपैकी प्रत्येक लघुकाला त्याच्या बैजिक पूरकाने गुणून मग केलेल्या त्यांच्या बेरजेबरोबर असतो, असे सिद्ध केले. या महत्त्वाच्या प्रमेयाला लाप्लास यांचेच नाव देण्यात आले आहे. न्यूटनीय गुयत्वाकर्षणाची संकल्पना संपूर्ण सूर्यकुलासाठी वापरणे हे लाप्लास यांनी आपल्या आयुष्यभराच्या कार्याचे ध्येय ठरविले होते आणि याची सुरुवात त्यांनी १७७३ मध्ये ‘गुरूची कक्षा सातत्याने आकुंचन पावत असल्याचे, तर शनीची सातत्याने प्रसारण पावत असल्याचे दिसते’ या विशेषेकरून क्लिष्ट अशा प्रश्नापासून केली. सूर्यकुलातील घटकांमधील परस्पर गुरुत्वाकर्षणीय आंतरक्रिया इतक्या जटिल होत्या की, या प्रश्नाचे गणितीय उत्तर काढणे अशक्य वाटत होते. यामुळे न्युटन यांनी सूर्यकुलाचा समतोल राखण्यासाठी ठराविक काळाने दैवी हा ईश्वरी मध्यस्थी आवश्यक आहे, असा निष्कर्ष काढला होता. लाप्लास यांनी ग्रहांच्या माध्य गती (सरासरी कोनीय वेग) स्थिर असतात असे सिद्ध केले आणि त्याकरिता ग्रहांच्या कक्षांच्या विकेंद्रता व क्रांतीवृत्ताच्या पातळीशी असलेला त्यांचा कल [⟶ कक्षा] यांची तृतीय घात असलेली पदेही विचारात घेतलेली होती. १७७३ मधील लाप्लास यांचा हा शोध भौतिकीय ज्योतिषशास्त्रातील न्यूटन यांच्यानंतरचा सर्वांत महत्त्वाचा शोध होता. या शोधाकरिता फ्रान्सच्या ॲकॅडेमी ऑफ सायन्सेसने लाप्लास यांना सहयोगी सदस्यत्वाचा बहुमान दिला.
आत्वांन लव्हॉयझर यांच्याबरोबर लाप्लास यांनी एक बर्फयुक्त उष्णतामापक तयार केला आणि १७८० मध्ये सजीव व निर्जीव प्रणालींच्या तुलनेसाठी त्याचा उपयोग केला. यावरून त्यांनी श्वसनक्रिया ही एक प्रकारची ज्वलनक्रियाच असल्याचे दाखविले या उष्णतामापकाचा उपयोग नंतर वायू रसायनशास्त्रातही करण्यात आला. त्यानंतर ग्रहांच्या विक्षोभांच्या (परस्परांतील गुरुत्वाकर्षणच्या परिणामांच्या ) ज्योतिषशास्त्रीय प्रश्नाकडे ते परत वळले आणि ग्रहांच्या कक्षांच्या विकेंद्रता व त्यांचे परस्परांशी असणारे कल नेहमी अल्प, स्थिर व स्वयं-सुधारक राहातील, असे १७८६ मध्ये सिद्ध केले. यामुळे विक्षोभांचे परिणाम संचही व विनाशक नसून स्थितीरक्षक व नियतकालिक आहेत उदा., गुरू व शनी यांच्या गतीतील विरुद्ध व दीर्घकालीन असमानता (अनुक्रमे प्रवेग व ॠण प्रवेग) ९२९ वर्ष आवर्तकाल असलेल्या बदलत्या परिणामामुळे उद्‌भवणाऱ्या आहेत आणि त्यामुळे या असमानता संचयी नसून नियतकालिक आहेत, असे लाप्लास यांनी दाखविले. गुरूच्या चंद्रांच्या माध्य गतींमधील नियतकालिक संबंधाचाही त्यांनी शोध लावला. लाप्लास यांच्या वरील सर्व संशोधनात सूर्यकुल अवकाशात अलग असून ते विखुरलेल्या द्रव्यापासून पूर्णपणे मुक्त आहे आणि सुर्य सद्यस्थितीत अमर्याद काळ राहील, असे गृहीत धरलेले होते.
लाप्लास यांनी १७८७ मध्ये चंद्राचा प्रवेग पृथ्वीच्या कक्षेच्या विकेंद्रतेवर अवलंबून आहे असे प्रतिपादन करून सूर्यकुलाच्या सैद्धांतिक वर्णनातील अखेरची दर्शनी विसंगती दूर केली. चंद्राची पृथ्वीभोवतीची माध्य गती प्रामुख्याने त्यांतील परस्पर गुरूत्वाकर्षणावर अवलंबून असली तरी सूर्याच्या चंद्रावरील ओढीमुळे ती थोडीशी कमी होते. तथापि, सूर्याची ही क्रिया इतर ग्रहांमुळे उद्‌भवणाऱ्या विक्षोभांनी पृथ्वीच्या कक्षेच्या विकेंद्रतेत निर्माण होणाऱ्या बदलावर अवलंबून असते. यामुळे जोपर्यंत पृथ्वीची कक्षा अधिक वर्तुळाकार होण्याची प्रवृत्ती असते तोपर्यंत चंद्राची माध्य गती प्रवेगीत होते व जेव्हा याउलट परिस्थिती असते तेव्हा चंद्राची गती कमी होते. यावरून ही गती खरोखरी संचयी नसून लक्षावधी वर्ष आवर्तकाल असलेली आहे, असा लाप्लास यांनी निष्कर्ष काढला.
इ. स. १७९६ मध्ये लाप्लास यांनी आपले ⇨खगोलीययामिकीमधील कार्य Exposition du system du monde या काहीशा सुबोध भाषेत लिहिलेल्या ग्रंथाद्वारे प्रसिद्ध केले. हा ग्रंथ गद्यरूप फ्रेंच लेखनाचा एक आदर्श मानला जातो. या ग्रंथात त्यांनी ‘अक्षीय परिभ्रमण करणाऱ्या एका वायुमय अभ्रिकेचे शीतलीकरण व आकुंचन होऊन सूर्यकुलाची उत्पत्ती झाली’ हे ‘अभिकीय गृहीतक’ मांडले [⟶ सुर्यकुल]. ग्रहांच्या उत्पत्तीसंबंधीच्या त्यानंतरच्या काळातील विचारसरणीवर या गृहीतकाचा फार मोठा प्रभाव पडला. इमॅन्युएल कांट यांनीही अशा स्वरूपाची संकल्पना १७५५ मध्ये मांडली होती. लाप्लास यांनी स्वतः केलेला गणितीय विकास व गुरुत्वाकर्षणाच्या नियमाचा अनुप्रयोग यांद्वारे मिळविलेले सिद्धांत व निष्कर्ष आणि विख्यात गणितज्ञांच्या तीन पिढ्यांनी केलेले गुरुत्वाकर्षणसंबंधीचे कार्य सारांशरूपाने १७९८ ते १८२७ या काळात पाच खंडांत Trait de mechanique celeste या ग्रंथाद्धारे प्रसिद्ध केले या ग्रंथात त्यांनी ग्रह व उपग्रह यांच्या गती तसेच त्यांचे विक्षोभ यांचे गणन करण्याच्या पद्धती योजून सूर्यकुलाचे संपूर्ण यामिकीय विवरण दिलेले होते. या ग्रंथामुळे लाप्लास यांना दिगंत कीर्ती प्राप्त झाली.
सर्वसामान्य वाचकासाठी संभाव्यतेच्या तत्वज्ञानाविषयी Essai Philosophique sur les probabilities हा सुबोध ग्रंथ १८१४ मध्ये लाप्लास यांनी प्रसिद्ध केला. हा ग्रंथ त्यांच्या Theorie analytique des probabilities या १८१२ मध्ये प्रथम प्रसिद्ध झालेल्या व्यापक व महत्त्वाच्या ग्रंथाच्या १८१४ मधील दुसऱ्या आवृत्तीला प्रस्तावना असलेल्या स्वरूपाचा होता. या दुसऱ्या ग्रंथात विशिष्ट घटना निसर्गात घडून येण्याच्या संभाव्यात गणितीय रीत्या वर्तविण्यासाठी गणन करण्याकरीता त्यांनी शोधिलेल्या अनेक गणितीय साधनांचे वर्णन केलेले आहे. त्यांनी आपल्या सिद्धातांचा सामान्य आकस्मिक घटनांचा (उदा., नाणे उडवून छाप वा काटा वर येणे अथवा फासा टाकून एखादा विशिष्ट आकडा वर येणे यांसारख्या घटनांच्या) बरोबरच विविध आविष्कारांच्या कारणांचा शोध घेणे, जन्म-मृत्यू, विवाह इत्यादींसंबंधीची आकडेवारी आणि भविष्यकालीन घटना यांकरिताही उपयोग केला. भौतिकी व ज्योतिषशास्त्र या विषयांतील संभाव्यता सिद्धांताच्या महत्त्वावरही त्यांनी भर दिलेला होता [⟶ संभाव्यता संभाव्यता सिद्धांत]. या ग्रंथाद्वारे त्यांनी शुद्ध गणितात महत्त्वाच्या कित्येक नव्या कल्पना [विशेषतः लाप्लास रूपांतराचा सिद्धांत ⟶ समाकल समीकरणे व रूपांतरे] प्रचारात आणल्या.
लाप्लास यांची आणखी एक महत्त्वाची कामगिरी म्हणजे त्यांनी ⇨वर्चस् या संकल्पनेचा केलेला विकास व तिचे लाप्लास समीकरणाद्वारे केलेले वर्णन ही होय. १७८५ मध्ये गोलांभाच्या गुरुत्वाकर्षणीय क्षेत्रांसबंधीच्या विख्यात संस्मरणिकेत हे त्यांचे कार्य प्रसिद्ध झाले. याद्धारे त्यांनी ⇨गोलीय हरात्मकविश्लेषणाचे तंत्रही पूर्णत्वास नेले.
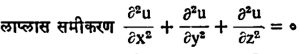हे एक क्षेत्र समीकरण आहे, म्हणजेच हे समीकरण गुरुत्वाकर्षणीय द्रव्यमान, विद्युत् भार, द्रायू (द्रव व वायू) प्रवाह इत्यादींमुळे निर्माण होणाऱ्या क्षेत्रात प्रत्येक बिंदूपाशी काय घडत आहे याचे वर्णन देते. हे समीकरण संपूर्ण सहततीमध्ये वर्चस् या भौतिक राशीच्या मूल्याशी संबंधित असते. वर्चस् फलन u हे प्रथमतः पूर्णपणे एक गणितीय राशी म्हणून प्रचारात आले व नंतर त्याला भौतिक अर्थ प्राप्त झाला. u ला निरनिराळे अर्थ (उदा., तापमान, वेग, वर्चस् इ.) दिल्यास या समीकरणाचा विद्युत् स्थितिकी, गुरूत्वाकर्षण, द्रायुगातिकी, चुंबकत्व, ध्वनी, प्रकाश, उष्णतेचे संवहन इत्यादींमधील सिद्धांतांत व्यापक उपयोग करता येतो, असे दिसून आले आहे. [⟶ गोलीय हरात्मके वर्चस् क्षेत्र सिद्धांत].
लाप्लास हे १७८५ मध्ये फ्रेंच ॲकॅडेमी ऑफ सायन्सेंसचे पूर्ण सदस्य झाले. कदाचित त्यांची राजकीय मते फारशी तीव्र नसल्याने फ्रेंच राज्यक्रांतीच्या काळात ते कारावास व फाशी यांतून बचावले असावेत. नेपोलियन बोनापार्ट यांना गणितात स्वाभाविक गोडी असल्याने त्यांनी या काळातील प्रसिद्ध गणितज्ञांना बक्षिसे दिली. लाप्लास १७९९ मध्ये केवळ सहा आठवडे नेपोलियन यांचे अंतर्गत मंत्री होते परंतु प्रशासक म्हणून त्यांची कामगिरी पसंत न पडल्याने त्यांना सिनेटर करण्यात आले. त्यांना काउंट ऑफ द एम्पायर हा किताब देण्यात आला. लाप्लास ब्यूरो द लाँजिट्यूड्सचे अध्यक्ष होते. मेट्रिक पद्धती संघटित करण्यास त्यांनी मदत केली. नंतरच्या काळात ते आर्कई या पॅरिसच्या उपनगरात राहू लागले. तेथे सी. एल्. बेर्‌तॉले या रसायनशास्त्रज्ञांच्या समवेत त्यांनी सोसायटी द आर्कई ही वैज्ञानिक संस्था स्थापन केली. बुरबाँ राजवटीच्या पुनरागमनानंतर अठरावे लूई यांनी त्यांना मार्की हा किताब दिला. लाप्लास हे केवळ स्वतःचा उत्कर्ष साधण्यास उत्सुक असलेले व दुसऱ्याचे संशोधन कार्य नामोल्लेखही न करता वापरणारे म्हणून गणितज्ञांत प्रसिद्ध असले, तरी त्यांनी इतर संशोधकांना अनेक प्रकारे मदत केली व फ्रेंच विज्ञानाच्या प्रगतीस सतत उत्तेजन दिले. ते पॅरिस येथे मृत्यू पावले. ॲकॅडेमी ऑफ सायन्सेसने त्यांचे संपूर्ण कार्य Euvres Completes (१८७८-९२) या शीर्षकाखाली चौदा खंडांत प्रसिद्ध केले.
काळीकर, मो. वि.; ओक, स. ज.