अपास्त

अपास्त: हा शांकव कुलातील एक वक्र होय [→ शंकुच्छेद].

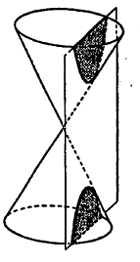
वृत्तशंकूच्या (वर्तुळाकृती पाया असलेल्या शंकूच्या) दोन्ही शाखांना छेदील अशा प्रतलाने (पातळीने) छेद घेतल्यास जो छेदवक्र मिळतो तो अपास्त होय. अपास्ताला विभक्त अशा दोन शाखा असतात. तसेच हा वक्र अनावृत्त (उघडा) आणि अनंतगामी आहे हे यावरून लक्षात येते. शांकव कुलातील सर्व वक्रांच्या बाबतीत वक्रावरील प्रत्येक बिंदूचे एका स्थिर बिंदूपासूनचे (या बिंदूला ‘नाभी’ म्हणतात) एका स्थिर) अंतर व एका स्थिर रेषेपासूनचे (या रेषेला ‘नियतरेषा’ म्हणतात) अंतर यांचे गुणोत्तर कायम (स्थिर) असते. या गुणोत्तराला ‘विकेंद्रता’ (इ) म्हणतात. अपास्ताच्या बाबतीत विकेंद्रतेचे मूल्य एकाहून अधिक (इ &gt १) असते. यावरून त्याचे बैजिक द्विघाती समीकरण काढता येते.

संदर्भ-अक्षांची योग्य निवड केल्यास पुढे दिल्याप्रमाणे अपास्ताचे समीकरण प्रमाणित स्परूपात काढता येते.

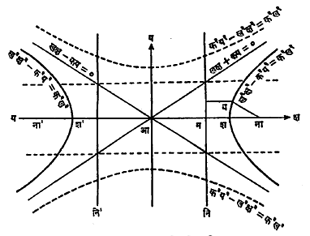समजा, ना हा स्थिर नाभिबिंदू आणि नि ही स्थिर नियतरेषा दिलेली  आहे. नाम हा नियतरेषेवर लंब टाकला. नाम लाइ : १ या गुणोत्तरात श, श’ या बिंदूत हरात्मकरीत्या विभागले (म्हणजे श या अंतर्गत  बिंदूने होणाऱ्या भागांचे गुणोत्तर नाश : शम आणि श’ या बाह्य बिंदूने होणाऱ्या भागांचे गुणोत्तर नाश‘ : श‘म सारखेच म्हणजे इ : १ येईल असे विभागणे), शश’ चा मध्यबिंदू आ हा आदिबिंदू आणि आना हा क्ष-अक्ष समजून य-अक्ष काढला. शश‘ = २ क समजले तर श आणि श’ यांचे सहनिर्देशक (स्थानदर्शक संख्या) अनुक्रमे (क, ०) आणि (-क, ०) असे होतील. जर मश ची लांबी ग मानली तर शना ची लांबी इ.ग होईल कारण शना : शम = इ : १ आहे. आता हरात्मक विभाजनाच्या गुणधर्माचा उपयोग करून  आश^२ = आम. आना असे लिहिता येते. म्हणजेच क^२ = ( क – ग)  ( क + इग). यावरून आना = क.इ आणि आम = क/इ असे दाखविता येईल. म्हणजेच ना चे सहनिर्देशक (कइ, ०)असून नियतरेषेचे समीकरण  क्ष = क/इ असे लिहिता येईल.

आता ब ( क्ष, य ) हा जर अपास्तावरील कोणताही बिंदू असला तर त्याचे ना पासूनचे अंतर आणि  नियतरेषेपासूनचे अंतर यांचे गुणोत्तर इ : १ इतके पाहिजे. म्हणून (क्ष – क)^२ + य^२ = इ ^२ ( क्ष-क/इ )^२ असले पाहिजे. म्हणून हे सोडवून आणि क^२ (इ^२ –१) याकरिता ख^२ घालून अपास्ताचे प्रमाणित समीकरण

किंवा ख ^२ क्ष^२ – क^२ य^२ = क^२ ख^२मिळते.

जर (क्ष, य) हा बिंदू अपास्तावर असेल म्हणजेच वरील समीकरणाची पूर्तता करीत असेल तर (क्ष,– य), (– क्ष, य) आणि (– क्ष, – य) हेही बिंदू अपास्तावर असले पाहिजेत. यावरून असे दिसून येईल की अपास्त हा वक्र क्ष– आणि य– अक्षांभोवती सममित (प्रमाणबद्ध) आहे. क्ष– आणि य– अक्षांस अनुक्रमे  जात्यछेदक आणि संयुग्म अक्ष असे म्हणतात. अपास्ताचे दोन बिंदू (हे अपास्ताच्या एकाच शाखेवर किंवा भिन्न शाखांवर असतील) जोडणाऱ्या रेषेस अपास्ताची जीवा म्हणतात. आ मधून जाणाऱ्या जीवेचा आ हा मध्यबिंदू असतो.आ ला अपास्ताचा केंद्रबिंदू म्हणतात अपास्ताच्या सममिततेवरून नाभी ना (क इ, ०) आणि नियतरेषा क्ष = क/इ यांच्याप्रमाणेच ना’ (–कइ, ०) आणि क्ष = –क/इ अनुक्रमे नाभी आणि नियतरेषा घेऊनही हाच अपास्त मिळतो. म्हणजेच अपास्ताला दोन नाभी आणि दोन नियतरेषा असतात.

ब हा अपास्तावरील कोणताही एक बिंदू असेल तर नाब आणि ना‘ब यांच्या लांबीतील फरक स्थिर ( = २ क) असतो असे सिद्ध करता येते. या गुणधर्माचा उपयोग करून अपास्ताची पुढील पर्यायी व्याख्या देणे शक्य आहे. जेव्हा एखादा बिंदू अशा तऱ्हेने फिरत असेल की, दोन स्थिर बिंदूपासूनच्या त्याच्या अंतरामधील फरक स्थिरांक आहे तेव्हा त्याचा बिंदूपथ हा अपास्त होय.

कोणत्याही  बिंदूपासून अपास्ताला दोन स्पर्शिका (स्पर्शरेषा) काढता येतात. तसेच कोणत्याही  बिंदूपासून अपास्ताला प्रलंब (लंबरूप) असतील अशा चार रेषा काढता येतात.

अपास्ताच्या अनंतस्थ बिंदूशी स्पर्शिका काढल्यास तिला अनंतस्पर्शिका म्हणतात. तिचे समीकरण पुढीलप्रमाणे मांडता येते. समजा, य = उक्ष + घ ही एक रेषा आहे. तिचे ख^२ क्ष^२ – क^२ य^२ = क^२ ख^२ याअपास्ताशी छेदनबिंदू काढण्याकरिता ही दोन्ही समीकरणे सोडवावी लागतील. यातून य चा निरास केला असता ख^२ क्ष^२–क^२ (उक्ष+घ )^२ = क^२ ख^२ असे समीकरण मिळते. याची बीजे क्ष_१ व क्ष_२ असल्यास ती छेदनबिंदूचे क्ष सहनिर्देशक दर्शवतील. जर वरील रेषा अनंतस्पर्शिका असेल तर क्ष_१ = क्ष_२ = ∞ असले पाहिजे. म्हणजे जर क्ष’= १/क्ष असा आदेश योजिला तर समीकरणाची दोन्ही बीजे शून्य असावी. म्हणजेच क^२ (ख^२ +घ^२)क्ष’^२ + २ क^२ उगक्ष’+ (क^२ उ^२ – ख^२) = ० याची बीजे शून्य असावी. असे होण्यास क^२ उघ = ० आणि  क^२उ^२ = ख^२ असले पाहिजे. म्हणजेच

यावरून

या अपास्ताच्या दोन अनंतस्पर्शिका होत हे सिद्ध होते.

जर क = ख असेल तर = अनंतस्पर्शिका य = क्ष आणि य = – क्ष ह्या परस्परांस लंब होतील आणि अपास्त क्ष ^२ – य ^२ = क^२होईल. अशा अपास्तास जात्य अपास्त म्हणतात. या ठिकाणी अनंतस्पर्शिका जर संदर्भ-अक्ष म्हणून वापरल्या तर अपास्ताचे समीकरण क्ष. य = स^२ (स स्थिरांक) असे दाखविता येते

या समीकरणाने दर्शविलेला वक्रही अपास्तच आहे, असे दाखविता येते (पहा : आ. २) या अपास्ताला

याचा संयुग्मी अपास्त असे म्हणतात.

ह्या संयुग्मनी अपास्ताच्याही अनंतस्पर्शिका असतात. 

 वरील विवेचनावरून असेही म्हणता येईल की, केंद्रबिंदू आ पासून अपास्ताला स्पर्शिका काढल्यास त्यांचे स्पर्शबिंदू अनंतस्थ असतात. म्हणजे या स्पर्शिका अपास्ताच्या अनंतस्पर्शिकाच   असतात. तसेच आ ची  स्पर्शजीवा ही  अनंतस्थ रेषा असते.

अपास्ताच्या नाभी व त्यांच्या संबंधित नियतरेषा ह्या परस्परांचे ध्रुव आणि ध्रुवीय रेषा असतात. [→   शंकु – च्छेद].

आगाशे, क.म.

“