पृष्ठताण

पृष्ठताण : द्रवाच्या पृष्ठाचे क्षेत्रफळ कमीत कमी करण्याची प्रवृत्ती असणारी व पृष्ठप्रतलात (पृष्ठाच्या पातळीत) कार्यकारी असणारी प्रेरणा. पृष्ठप्रेरणेमुळेच किंवा व्यापक दृष्टीने पाहता आंतरपृष्ठीय प्रेरणेमुळेच द्रवाकडून घन पदार्थ ओले होणे किंवा न होणे, दिव्याच्या वातीतून गुरुत्वाकर्षणाच्या विरूद्ध तेल चढणे वगैरे आविष्कार घडून येतात. रेवणीय प्रेरणा : पृष्ठताणाच्या स्पष्टीकरणार्थ द्रवातील रेवणीय प्रेरणांची माहिती करून घेणे आवश्यक आहे. रेवणीय प्रेरणा दोन प्रकारच्या असतात : (१) आसंजक प्रेरणा किंवा आसंजन, (२) संसंजक प्रेरणा किंवा संसंजन.

आसंजन ही दोन निरनिराळ्या पदार्थांच्या (विजातीय) रेणूंमधील आकर्षणाची प्रेरणा होय. ह्या प्रेरणेचे मूल्य निरनिराळ्या पदार्थांच्या जोड्यांसाठी वेगवेगळे असते. संसंजन ही एकाच पदार्थाच्या (सजातीय) रेणूंमधील आकर्षणाची प्रेरणा होय. प्रेरणा सर्वसामान्य गुरुत्वीय प्रेरणेपेक्षा वेगळी असून ती दोन रेणूंमधील वाढत्या अंतराप्रमाणे (अधिक) जलद रीत्या कमी होत जाते. जेव्हा रेणूंमधील अंतर अगदी कमी (सु. ४ × १०–१० मी.) असते तेव्हा ही प्रेरणा अधिक जोरदार असते आणि ठराविक अंतरापर्यंतच ही सक्रिय राहते. ज्या जास्तीत जास्त अंतरापर्यंत संसंजन प्रेरणा कार्य करू शकते, त्या अंतरास रेवणीय पल्ला असे म्हणतात. या रेवणीय पल्ल्याच्या अंतराइतकी त्रिज्या व कोठलाही रेणू हा मध्य घेऊन काढलेल्या गोलास त्या रेणूचा ‘ प्रभाव गोल ’ असे म्हणतात. फक्त त्याच्या प्रभावाच्या गोलात असलेल्या रेणूंच्या प्रेरणांचाच त्या रेणूवर परिणाम होतो.

 आ.१ मध्ये दाखविल्याप्रामाणे द्रवात खोलवर असलेल्या अ रेणूवर त्याच्या सर्व बाजूंस प्रभाव गोलात असलेल्या रेणूंच्या आकर्षक प्रेरणा कार्य करतात. ह्या सर्व आकर्षक प्रेरणांच्या निष्पन्न प्रेरणेचे मूल्य शून्य होते. परंतु द्रवाच्या मुक्त पृष्ठभागाजवळ असलेल्या इ रेणूवर निष्पन्न प्रेरणा शून्य होणार नाही. कारण या ठिकाणी प्रभाव गोलाचा काही भाग हवेत जातो. अशा स्थितीत निष्पन्न प्रेरणा रेणूला द्रवाच्या अंतर्भागात खेचते म्हणजेच ती अंतर्मुखी असते. जे रेणू द्रवाच्या पृष्ठभागाजवळ अथवा पृष्ठभागावर असतील त्या प्रत्येकाच्या प्रभाव गोलाचा कमी अधिक भाग द्रवाच्या बाहेर राहतो. अशा सर्व रेणूंवर अंतर्मुखी निष्पन्न प्रेरणा कार्यान्वित होते. ही प्रेरणा मुक्त पृष्ठभागाजवळच्या अतिशय पातळ थरातच क्रियाशील असते. या थराला पृष्ठपटल म्हणतात व त्याची जाडी प्रभाव गोलाच्या त्रिज्येइतकी असते. रेणूवरील अंतर्मुखी प्रेरणांमुळे स्वतःच्या मुक्त पृष्ठाचे क्षेत्रफळ जितके कमी होईल तितके कमी करण्याची द्रवाची प्रवृत्ती असते. कारण त्यामुळे द्रवाची ऊर्जा किमान होते. विशिष्ट आकारमानासाठी गोलाचे पृष्ठक्षेत्र सर्वांत कमी असते. त्यामुळे द्रवाचा बिंदू गोलाकार रूप धारण करतो. पृष्ठक्षेत्र शक्य तितके कमी बनविण्याच्या प्रयत्नात द्रव अशा रीतीने वागतो की, जणू त्यावर एखादे ताणलेले स्थितिस्थापक (ताण काढून घेतला असता मूळ स्थितीत परत येणारे) आवरण आहे.

अशा आवरणाची प्रवृत्ती आकुंचन पावण्याकडे असते. द्रवाचे पृष्ठक्षेत्र शक्य तितके कमी करण्याचा प्रयत्न करणाऱ्या द्रवाच्या पृष्ठभागातील प्रेरणेला पृष्ठताण म्हणतात. त्याची व्याख्या पुढीलप्रमाणे करता येईल. प्रभाव गोलाच्या त्रिज्येइतकी जाडी असलेल्या द्रवाच्या पृष्ठभागावरील थरात एकक लांबी असलेल्या कोणत्याही कल्पित रेषेवरील प्रत्येक बिंदूवर रेषेला लंब दिशेने लागू होणाऱ्या व पृष्ठप्रतलात असलेल्या प्रेरणेला पृष्ठताण म्हणतात. पृष्ठताणाचे एकक सी. जी. एस. (सेंटीमीटर-ग्रॅम-संकद) पद्धतीत डाइन/सेंमी. आणि एम. के. एस. (मीटर-किलोग्रॅम-सेकंद) पद्धतीत न्यूटन/मी. आहे. पृष्ठताण व पृष्ठऊर्जा : वर दर्शविल्याप्रमाणे पृष्ठताणामुळे पृष्ठभाग आकुंचन पावण्याचा प्रयत्न करतो. म्हणून द्रवाच्या अंतर्भागातून रेणू पृष्ठभागावर आणून पृष्ठभागाचे क्षेत्र जर वाढविले, तर पृष्ठभागातील रेणूंमध्ये असणाऱ्या संसंजक प्रेरणेविरूद्ध कार्य केले जाते. हे कार्य करण्यासाठी जी ऊर्जा खर्च केली जाते, ती द्रवाच्या पृष्ठात स्थितिज ऊर्जेच्या रूपात साठविली जाते. द्रवपृष्ठाचे एकक क्षेत्र वाढविण्यासाठी जे कार्य करावे लागते त्याला पृष्ठऊर्जा म्हणतात. सी. जी. एस. पद्धतीत पृष्ठऊर्जेचे एकक अर्ग/सेंमी.२ आणि एम. के. एस. पद्धतीत जूल/मी.२ आहे. समताप (तापमान न बदलणाऱ्या) स्थितीत द्रवाचा पृष्ठताण व पृष्ठऊर्जा समान असतात. ही गोष्ट खालील प्रयोगावरून सिद्ध करता येते.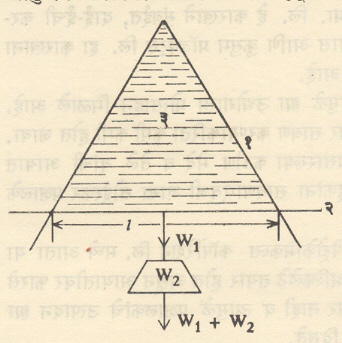   

आ. २ मध्ये दाखवल्याप्रमाणे प्रयोगात एक साधा तारेचा तुकडा इंग्रजी उलट्या V अक्षराच्या आकारात वाकवून त्यावर तारेचा दुसरा एक तुकडा घर्षणाशिवीय सरकू शकेल अशा तऱ्हेने लावण्यात येतो. जर सरकत्या तारेचे वजन (W1 ग्रॅ.) फार नसेल, तर तारेची चौकट साबणाच्या विद्रावात बुडवून वर काढली असता सरकती तार खाली न पडता, तयार झालेल्या साबणाच्या विद्रावाच्या पटलामुळे वरच्या बाजूला खेचली जाते. समतोल स्थितीत ठेवण्यासाठी सरकत्या तारेला थोडे जास्त वजन (W2 ग्रॅ.) लावावे लागते. अशा स्थितीत तारेवर लागणारी अधोमुखी प्रेरणा F=W1 + W2 होईल. जर पटलाचे तापमान बदलत नाही असे मानले, तर F व पृष्ठताणीय प्रेरणा यांचा समतोल होऊन सरकती तार स्थिर राहील.

साबणाच्या विद्रावाचे पटल जरी पातळ असले, तरी त्याची जाडी रेणूच्या व्यासापेक्षा बरीच जास्त असते. या पटलाला दोन (एक पुढचा व दुसरा मागचा) पृष्ठभाग असतात व या प्रत्येक पृष्ठात तारेच्या एकक लांबीवर T ही पृष्ठताणीय प्रेरणा लागू होईल. सरकत्या तारेची लांबी l आहे व साबणाच्या पटलाचा पृष्ठताण T आहे असे गृहीत धरल्यास सरकत्या तारेवर ऊर्ध्वमुखी कार्य करणारी प्रेरणा 2l.T होईल पटल समतोल स्थितीत असल्यामुळे अधोमुखी व ऊर्ध्वमुखी प्रेरणा समान होतील म्हणजे F=2l .T पटलाच्या समताप स्थितीत सरकती तार समजा X अंतर खाली सरकवली. यामुळे पटलाच्या पृष्ठभागाचे क्षेत्र प्रत्येक बाजूस l.X ने वाढेल म्हणून F प्रेरणेविरुद्ध पृष्ठाचे क्षेत्र वाढविण्यासाठी करावे लागणारे कार्य W खालीलप्रमाणे लिहिता येते.

                                                               W= F.X = 2 l.Tx = 2 TA

              यात      2 A = 2 l.x    आहे. यावरून समताप स्थितीत पटलाचे एकक क्षेत्रफळ वाढविण्यासाठी करावे लागणारे कार्य   W/2A = T   असे दिसून येईल. परंतु      W/2A       ही पृष्ठऊर्जा आहे म्हणून समताप परिस्थितीत एकक क्षेत्रफळाची पृष्ठऊर्जा व पृष्ठताण समान असतात हे सिद्ध होते. कैशिकता : जेव्हा कोणत्याही द्रवाचा घन पदार्थाशी संपर्क होतो तेव्हा रेणवीय प्रेरणांमुळे घनाजवळील द्रवाचा पृष्ठभाग सामान्यपणे वक्र होतो. स्पर्शबिंदू द्रवाच्या पृष्ठभागास काढलेली स्पर्शरेषा व घनाचा पृष्ठभाग यांतील द्रवाच्या आत होणाऱ्या कोनास, त्या द्रव व घनाच्या जोडीचा स्पर्शकोन म्हणतात. एखादी घन पट्टी द्रवात बुडविली असता, द्रवाचे मुक्त पृष्ठ घनास ज्या कोनात (φ) स्पर्श करील त्याला स्पर्शकोन म्हणतात. जेव्हा द्रव घनास ओला करू शकतो तेव्हा हा कोन लघू असतो [आ. ३ (अ)].

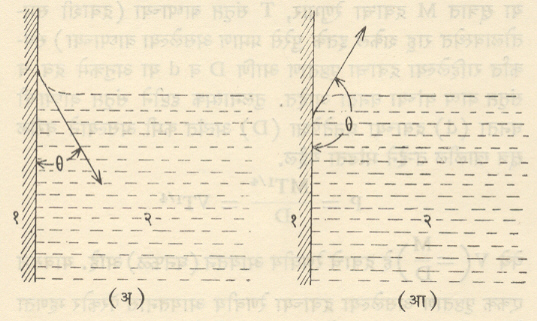पारा काचेस ओला करू शकत नाही अशा वेळी स्पर्शकोन विशाल असतो [आ. ३(आ)]. 

दोन्ही टोकांस उघडी असलेली केशनलिका (सूक्ष्म व्यासाची नलिका) तिला ओली करणाऱ्या द्रवात बुडविली असता, द्रव गुरुत्वीय प्रेरणेविरुद्ध त्या नलिकेतून वर चढतो. या आविष्कराला कैशिकता किंवा केशाकर्षण म्हणतात. भांड्यात ठेवलेल्या द्रवाच्या मुक्त पृष्ठभागापासून केशनलिकेत द्रवाची पातळी h सेंमी. उंचीवर आहे असे समजू (आ.४) केशनलिकेची आतील त्रिज्या r व द्रवाची घनता p आहे असे समजू.

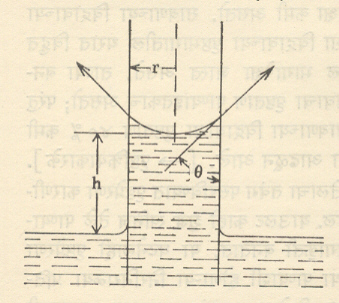नलिकेतील द्रवावर कार्य करणाऱ्या प्रेरणा खालीलप्रमाणे आहेत. (१) द्रवाच्या मुक्त पृष्ठभागावर नळीत चढलेल्या द्रवाच्या वजनामुळे अधोमुखी प्रेरणा व (२) पृष्ठताणामुळे लागणारी ऊर्ध्वमुखी प्रेरणा. (१) नलिकेतील द्रवाचे वजन = आकारमान × pg = πr2 hρg येथे g हा गुरुत्वीय प्रवेग आहे. जर नलिकेचा आतील व्यास अतिशय कमी असेल, तसेच नलिकेच्या सर्व ठिकाणी तो सारखाच असेल, तर तिच्या बाहेरील मुक्त पृष्ठाभोवती किंचित चढलेले द्रवाचे आकारमान, h उंची असलेल्या स्तंभातील द्रवाच्या मानाने उपेक्षणीय ठरते. म्हणून नलिकेतील द्रवाचे आकारमान  πr2h   धरता येते आणि द्रवावरील अधोमुखी प्रेरणा वर दाखविल्याप्रमाणे,   πr2   hρg  होते. (२) मुक्त पृष्ठ नलिकेला वर्तुळात भिडते. त्यामुळे वर्तुळाची त्रिज्या  r  होईल. पृष्ठताण (T) वर्तुळाच्या प्रत्येक बिंदूवर कार्य करीत असल्यामुळे पूर्ण ऊर्ध्वमुखी प्रेरणा   2π rT cos  Θ  होईल. येथे Θ हा स्पर्शकोन आहे. समतोल स्थितीत,

                                                                    2πrT cos Θ = πr2 hρg

                                                                        T= rghρ /2 cos Θया समीकरणावरून द्रवाचा पृष्ठताण T काढता येतो. कैशिकतेच्या या गुणधर्मामुळे गुरुत्व प्रेरणेविरुद्ध दिव्यातील तेल वातीच्या वरील टोकास पोहोचते.तापमानाचा परिणाम : द्रवाचा पृष्ठताण वाढत्या तापमानाबरोबर कमी होतो आणि त्याच्या सीमांत तापमानाला पृष्ठताण नाहीसा होतो. जर तापमान बदल कमी असेल, तर पृष्ठताण व तापमान व्यस्त प्रमाणात बदलतात. जर Tt हा t° से. ला. पृष्ठताण असेल आणि T0 हा o° से.ला पृष्ठताण असेल, तर

                                                                          Tt = T0 (1 – αt)

हे समीकरण मिळते. यात α हा पृष्ठताणाचा तापमान गुणांक आहे. एटव्हॅश – रॅम्झी – शिल्ड्स सूत्र (आर्. बी. फोन एटव्हॅश, डब्ल्यू. रॅम्झी व जे. शिल्ड्स यांच्या नावाने ओळखण्यात येणारे सूत्र) पृष्ठताणामध्ये तापमानातील फरकामुळे होणारा बदल जास्त अचूक दर्शवते ते सूत्र पुढील प्रमाणे आहे :

                                                                  T(M/p)2/3 = k (Θc -Θ- d)

येथे T = पृष्ठताण, Θ= द्रवाचे निरक्षेप तापमान, M = द्रवाचा रेणुभार, ρ = द्रवाची घनता, Θ C = निरपेक्ष सीमांत तापमान आणि k व d हे स्थिरांक आहेत.

द्रवाचा वक्रपृष्ठभाग : आ. ५ मध्ये दर्शविल्याप्रमाणे समजा की, ABCD हा द्रव पटलाच्या वक्रपृष्ठाचा एक लहान आयत आहे. आयताच्या बाजूंच्या लांब्या x व y आहेत. तसेच त्याच्या प्रधान वक्रत्रिज्या अनुक्रमे R1 व R2 आहेत. पटलाच्या समतोल स्थितीमध्ये त्याच्या अंतर्वक्र बाजूला दाब-आधिक्य P आहे असे गृहीत धरू. जर पटलाच्या लंब दिशेने काल्पनिक किंचित स्थानांतर δz केले, तर ते पटल थोडे ताणले जाईल व त्यामुळे पटलाला A’B’C’D’ ही स्थिती प्राप्त होईल. दाबामुळे झालेले कार्य (W) पुढीलप्रमाणे मांडता येते.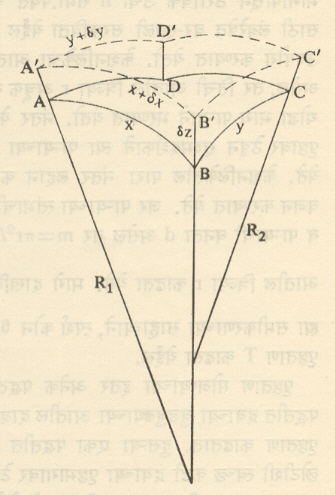                                                  W = p.xy.δz

जर पटलाच्या बाजू δx, δy या मूल्यांनी वाढल्या, तर त्याच्या क्षेत्रफळात

                              (x+δx) (y+δy) – xy = x. δy + y.δx

इतकी वाढ होईल. (येथे δx आणि δy ही फार लहान असल्यामुळे त्यांचा गुणाकार उपेक्षणीय समजण्यात आला आहे).म्हणून पृष्ठताण T विरुद्ध झालेले कार्य T (x.δy + y.δx)होते. पृष्ठताणाविरुद्ध झालेले कार्य व दाब-आधिक्याच्या द्वारा झालेले कार्य समान असले पाहिजे, म्हणून

                   p.xy.δz = T (x.δy + y.δx)पण आकृतीवरून असे दाखविता येते की,                     δx = x.δz/R1 δy = y.δz/ R2म्हणून δy व δx यांची मूल्ये घालता व xyδz ने भागून                   p = T (1/R1 + 1/R2) …     …     (१)हे समीकरण मिळते. जर दोन वक्रपृष्ठांपैकी एक अंतर्वक्र व दुसरे बहिर्वक्र असेल, तर वक्रता त्रिज्यांची चिन्हे परस्पर विरोधी होतील तेव्हा                        P = T (1/R1 – 1/R2)…    …    …    (२)असे समीकरण मिळेल. समीकरण (१) व (२) यांचा समन्वय करता                   P = T (1/R1 +- 1/R2)असे येईल. पटलाला दोन पृष्ठे असल्यास दाब-आधिक्य p खालील समीकरणाने दिले जाते.                      P = 2T (1/R1 +- 1/R2) पृष्ठताणाचे मापन : काचेच्या केशनलिकेत वर चढलेल्या द्रवाच्या स्तंभाच्या उंचीवरून पृष्ठताण (T) काढण्याच्या पद्धतीमध्ये प्रथम केशनलिका पूर्णपणे साफ करण्यात येते. नंतर काचेच्या पात्रात घेतलेल्या द्रवात या केशनलिकेचा खालील भाग बुडवून ती उदग्र रेषेत ठेवण्यात येते. कैशिकतेमुळे पात्रातील द्रव केशनलिकेत द्रवाच्या पृष्ठभागापासून ठराविक उंची h सेंमी. पर्यंत चढेल. उंची h मोजण्यासाठी लंबरेषेत वर-खाली सरकविता येईल अशा चल सूक्ष्मदर्शकाचा उपयोग करण्यात येतो. केशनलिकेचा आतला व्यास सर्वत्र सारखा असेल, तर तिची आतील त्रिज्या r अचूक रीत्या मोजण्यासाठी तिचा थोडा भाग पाऱ्याने भरण्यात येतो. नंतर केशनलिका क्षैतिज समतल पृष्ठावर ठेवून सूक्ष्मदर्शकाने त्या पाऱ्याच्या स्तंभाची लांबी मोजण्यात येते. केशनलिकेतील पारा नंतर लहान काचपात्रात घेऊन पाऱ्याचे वजन करण्यात येते. जर पाऱ्याच्या स्तंभाची लांबी l व त्याचे वजन m व पाऱ्याची घनता d असेल तर   m = πr2l.d ह्यावरून केशनलिकेची आतील त्रिज्या r काढता येते. मागे दाखविल्याप्रमाणे T = rghρ/2cosθ ह्या समीकरणाच्या साहाय्याने, स्पर्श कोन  θ माहीत झाल्यास, द्रवाचा पृष्ठताण T काढता येईल. पृष्ठताण मोजण्याच्या इतर अनेक पद्धती प्रचारात आहेत. एका पद्धतीत द्रवाच्या बुडबुड्याच्या आतील दाब-आधिक्य मोजून त्यावरून पृष्ठताण काढतात. दुसऱ्या एका पद्धतीत प्लॅटिनमाच्या तारेची एक छोटीशी स्वच्छ कडी द्रवाच्या पृष्ठभागावर टेकवतात व ती द्रवापासून अलग करण्यासाठी लागणाऱ्या किमान प्रेरणेचे मापन करतात. त्यावरून पृष्ठताण काढता येतो. ही पृष्ठताण काढण्याची सर्वांत अचूक पद्धती असून तिच्याकरिता ‘पृष्ठताण तराजू’ हे खास उपकरण तयार करण्यात आले आहे. द्रवाच्या पृष्ठभागावर ज्ञात कंप्रतेचे (दर सेकंदास होणाऱ्या कंपनांच्या संख्येचे) तरंग निर्माण करून त्यांची तरंगलांबी मोजतात. त्यावरून पृष्ठताण काढण्याची एक पद्धती लॉर्ड रॅली (जे. डब्ल्यू. स्ट्रट.) यांनी शोधून काढली आहे.

पॅरकोर : पॅरकोर ही अनुभवनिर्णित राशी असून ती द्रवाच्या पृष्ठताण, रेणुभार व घनता यांचे फलन आहे. डी. बी. मॅक्डॉनल्ड यांनी पूर्वी मांडलेल्या प्रायोगिक पुराव्याच्या आधारे १९२४ मध्ये एस्. सुगडेन यांनी पॅरकोर P चे अनुभविक सूत्र पुढीलप्रमाणे दिले.                                                                                     P =     MT1/4

                                                                                                ——-                                                                                                   D-dया सूत्रात M द्रवाचा रेणुभार, T संतृप्त बाष्पाच्या (द्रवाशी समतोलावस्थेत राहू शकेल इतके पुरेसे प्रमाण असलेल्या बाष्पाच्या) संपर्कात राहिलेल्या द्रवाचा पृष्ठताण आणि D व d या अनुक्रमे द्रव व संतृप्त बाष्प यांच्या घनता आहेत. तुलनात्मक दृष्टीने संतृप्त बाष्पाची घनता (d) द्रवाच्या घनतेपेक्षा (D) अत्यंत कमी असल्याने वरील सूत्र खालील तऱ्हेने मांडता येईल.                                                                               P = MT1/4    =  VT1/4

                                                                                                              ——                                                                                                                   Dयेथे V (=M/D) हे द्रवाचे रेणवीय आयतन (घनफळ) आहे. यावरून एकक पृष्ठताण असलेल्या द्रवाच्या रेणवीय आयतनास पॅरकोर म्हणता येईल. निरनिराळ्या द्रवांचे पृष्ठताण ज्या वेगवेगळ्या तापमानांना एकसारखे होतील त्या तापमानांना, द्रवांचे पॅरकोर, त्यांच्या रेणवीय आयतनाशी समप्रमाणात असतात. रासायनिक संरचना निश्चित करण्यासाठी पूर्वी पॅरकोरचा उपयोग करीत असत परंतु आता ही पद्धत अशास्त्रीय समजली जाते व हिच्यापेक्षा जास्त चांगल्या पद्धतीही उपलब्ध झालेल्या आहेत.

विद्रावाचा पृष्ठताण : जेव्हा पदार्थ पाण्यात अतिशय विद्राव्य (विरघळणारा) असतो तेव्हा विद्रुत रेणूंचे पाण्याच्या रेणूंशी प्रबल आकर्षण असते. पाण्याच्या रेणूंच्या एकमेकांशी असलेल्या आकर्षणापेक्षा वरील आकर्षण जर अधिक जोरदार असेल, तर विद्रावाच्या पृष्ठभागावर विद्रुत रेणू वास्तव्य करतात. त्यामुळे पृष्ठऊर्जेत वाढ होते आणि म्हणून पृष्ठताणही वाढतो. पुष्कळशा अकार्बनी पदार्थांच्या (उदा., झिंक सल्फेट) जलीय विद्रावांच्या बाबतीत असे होते. तथापि विद्रावाच्या स्थितिज ऊर्जेचा कल लघुतम मूल्यांक प्राप्त करण्याकडे असल्यामुळे विद्रुत रेणू विद्रावाच्या आतील भागात खेचले जातात. याचाच अर्थ विद्रुत संहती (विरघळलेल्या पदार्थांचे प्रमाण) विद्रावाच्या पृष्ठाभागातील थरात आतील भागापेक्षा कमी होईल. त्याचप्रमाणे जेव्हा विद्रुत पदार्थ अल्प प्रमाणात विद्राव्य असेल तेव्हा विद्रावाच्या पृष्ठभागातील थरात एकमेकांशी प्रबल आकर्षण असणाऱ्या पाण्याच्या रेणूंची जागा काही विद्रुत रेणू घेतात. त्यामुळे विद्रावाचा पृष्ठताण शुद्ध विद्रुताच्या पृष्ठताणापेक्षा कमी असतो. साबणाच्या विद्रावाच्या बाबतीत असेच होते. अशा विद्रावाच्या पृष्ठभागातील थरात विद्रुत संहती विद्रावाच्या आतील भागापेक्षा जास्त असते. ताज्या बनविलेल्या साबणाच्या विद्रावाचा पृष्ठताण पाण्याइतकाच असतो परंतु समतोल पाप्त झाल्यावर साबणाच्या विद्रावाचा पृष्ठताण ४०% कमी होतो, असे लॉर्ड रॅली यांना आढळून आले. [⟶  पृष्ठक्रियाकारके].

पृष्ठतवंग: पाण्यावर तेलाचा तवंग पसरविण्यात पृष्ठप्रेरणा कारणीभूत असतात उदा., एरंडेल. याउलट काही शुद्ध खनिज तेले पाण्यावर न पसरता त्यावर भिंगाकृती बनतात. या घटनेलाही पृष्ठप्रेरणा कारणीभूत आहेत. तेलाच्या पाण्याशी होणाऱ्या निरनिराळ्या प्रतिक्रिया रासायनिक अन्योन्य क्रियेवर अवलंबून असतात. पसरणारी तेले पृष्ठताण कमी करतात. भिंगाकृती बनणाऱ्या तेलांचे रेणू पाण्याच्या रेणूच्या संगतीत राहण्यापेक्षा एकमेकांशी दृढ सहचरण करण्याचे पसंत करतात. लॉर्ड रॅली आणि इतरांच्या संशोधनावरून असे निश्चित स्वरूपात सांगता येते की, जी तेले पाण्यावर पसरतात ती पृष्ठभागावर तेलाच्या रेणूंचा एकस्तर (एका रेणूच्या जाडीचा स्तर) बनवितात. पाण्याच्या पृष्ठभागावर ह्या रेणूंची रचना ठराविक पद्धतीची असते. प्रत्येक रेणूचा पाण्यात विद्राव्य अथवा ध्रुवीय भाग पाण्याच्या पृष्ठभागावर असतो आणि त्याचा पाण्यात अविद्राव्य भाग पाण्याच्या पृष्ठभागापासून दूर जाण्याचा प्रयत्न करतो. जी तेले पाण्यावर पसरत नाहीत त्यांच्या रेणूंमध्ये पाण्यात विद्राव्य असा भाग नसतो, म्हणून ते पाण्याच्या पृष्ठभागावर एकत्र येऊन भिंगाकृती बनवितात. पाण्यावरील तेलाचा तंवग ‘वायुरूप’ किंवा संघटित स्वरूपाचा असू शकतो. वायुरूप तंवगात तेलाचा प्रत्येक रेणू त्याच्या शेजारच्या रेणूपासून दूर असतो, तर संघटित तवंगात तेलाचे रेणू गर्दी करून एकत्र राहतात. एक-रेणुस्तर : एक-रेणुस्तर किंवा एकस्तर म्हणजे विशिष्ट द्रव्याच्या एका रेणूइतक्या जाडीचा पातळ थर होय. पदार्थांच्या आंतरपृष्ठावरील पातळ स्तरामुळे घर्षण व झीज कमी करणे, गंजण्याची क्रिया कमी करणे, पायस (एका द्रवाचे सूक्ष्म बिंदू दुसऱ्या लोंबकळत्या स्थितीत असलेले मिश्रण) व फेस यांना स्थैर्य देणे, निर्जल प्रदेशातील जलाशयापासून बाष्पीभवनामुळे होणारा पाण्याचा अपव्यय कमी करणे अशी विविध कार्ये होतात. पाण्याचे प्रदूषण कमी करण्यासाठी त्याच्यावरील प्रदूषकांच्या स्तराचे निराकरण करणे जरूर असते. खनिजतेलाचे परिष्करण व इतर अनेक रासायनिक उद्योगधंद्यांत उत्प्रेरकांचे (रासायनिक विक्रियेची त्वरा बदलणाऱ्या पण विक्रियेच्या शेवटी मूळ स्वरूपातच राहणाऱ्या पदार्थांचे) कार्य अशा पातळ स्तरांद्वाराच होत असते. जीवविज्ञानातील कित्येक गुंतागुंतीच्या प्रक्रिया प्रथिने, कोलेस्टेरॉल किंवा तत्सम रसायनांच्या पातळ स्तरांतून होत असतात. म्हणून अशा स्तरांच्या गुणधर्मांचा अभ्यास करणे फार उपयुक्त आहे. पाण्याच्या अगदी स्वच्छ मुक्त पृष्ठावर (ईथरासारख्या) बाष्पनशील (बाष्परूपाने उडून जाणाऱ्या) द्रवात स्टिअरिक अम्लासारख्या पदार्थाच्या विद्रावाचा थेंब टाकल्यास त्या पृष्ठावर विद्रुत द्रव्याचा एकस्तर तयार होतो. या स्तराचा दाब एका खास उपकरणाने मोजता येतो. विशेष प्रक्रिया करून अशा स्तराचे इलेक्ट्रॉन सूक्ष्मदर्शकाच्या साहाय्याने परीक्षण करता येते. अशा प्रयोगावरून त्या विद्रुताच्या रेणूच्या काटच्छेदाचे मान काढता येते. त्याचप्रमाणे स्तराची पृष्ठभाग झाकण्याची क्षमताही काढता येते. अशा प्रयोगावरून गंज प्रतिबंधनासाठी योग्य अशा द्रव्याची निवड करता येते. पृष्ठवक्रता व पावसाच्या बिंदूंची घडण : संतृप्त बाष्पदाब द्रवाच्या सपाट पृष्ठापेक्षा द्रवाच्या अंतर्वक्र पृष्ठावर कमी असतो व बहिर्वक्र पृष्ठावर जास्त असतो म्हणून सपाट पृष्ठसंबंधात संतृप्तता असलेल्या जागेत जर पाण्याचा बिंदू ठेवला, तर त्या भोवतालच्या बाष्पाचा दाब बिंदूच्या संतृप्त बाष्पदाबाइतका वाढविण्यासाठी बिंदूच्या बाष्पीभवनास सुरुवात होईल. परंतु बिंदूचे बाष्पीभवन होत असता त्याची त्रिज्या कमी होते अथवा त्याची बहिर्वक्रता वाढते. त्यामुळे त्याचा संतृप्त बाष्पदाब वाढतो. यामुळे बिंदूंच्या बाष्पीभवनाची त्वरा वाढते. ह्याचा अर्थ अतिशय लहान बिंदू तयार झाल्यावर लगेच त्याच्या बाष्पीभवनास सुरुवात होते आणि म्हणून संतृप्त बाष्पाचे मोठ्या बिंदूत रूपांतर होत नाही. पाण्याच्या वाफेच्या द्रवीभवनाने घडून येणाऱ्या पावसाच्या घटनेशी ह्या गोष्टीचा महत्त्वाचा संबंध आहे. यावरून स्पष्ट होते की, अतिसूक्ष्म बिंदू द्रवीभवन क्रियेने वाढून मोठा बिंदू होण्याऐवजी त्याचा आकार कमी होतो. धूर अथवा धूलिकणांच्या मर्यादित विस्तारामुळे त्यांचा पृष्ठभाग सर्वसाधारणपणे सपाट म्हणता येईल. असे कण जर संतृप्त बाष्पात असतील, तर बाष्पाचे द्रवीभवन होऊन बिंदू तयार होण्यात येणाऱ्या सुरुवातीच्या अडचणी, अशा कणांच्या बाबतीत राहणार नाहीत. जसा बिंदू वाढेल तसा त्याचा संतृप्त बाष्पदाब कमी होईल आणि म्हणून त्याची बाष्पीभवनाची प्रवृत्ती कमी होईल. म्हणजेच द्रवीभवनास एकदा सुरुवात झाली की, तयार होणारा प्रत्येक बिंदू वाढत राहील. धूलिमय वातावरणात तापमान कमी झाल्याने तयार होणाऱ्या संतृप्त बाष्पापासून ढग अथवा धुके बनते. तसेच धूलिहीन वातावरणात दवबिंदूंपेक्षा (ज्या तापमानास हवा जलबाष्पाने संतृप्त होते त्या तापमानापेक्षा) तापमान कमी झाले असताही लवकर द्रवीभवन होत नाही. ह्या गोष्टी वरील विवेचनावरून समजून येतील. जलबिंदू विद्युत् भारित केल्यास त्यामुळे बिंदूच्या पृष्ठावर एक प्रकारचा दाब निर्माण होतो त्याला विद्युत् स्थितिकीय दाब असे म्हणतात. या दाबामुळे बिंदूचे आकारमान वाढण्याची प्रवृत्ती निर्माण होते. म्हणजेच पृष्ठताणाच्या विरुद्ध प्रकारचा परिणाम होतो व मोठे जलबिंदू तयार होण्यास मदत होते. सी. टी. आर्. विल्सन यांच्या बाष्प कोठीत आल्फा-कणांचे मार्ग आरेखित होतात त्याचे तत्त्व हेच आहे. [⟶  कण अभिज्ञातक]. पायस व फेस : दोन द्रवांपैकी एक द्रव प्रकृतीने जलीय असला, तर अशा दोन द्रवांच्या झालेल्या मिश्रणास पायस म्हणतात. पायसाचे सर्वसाधारण दोन प्रकार आहेत : (१) तेलात — पाणी आणि (२) पाण्यात — तेल. तेल ही संज्ञा स्थूलमानाने ‘पाण्यात अविद्राव्य प्रवाही पदार्थ’ या अर्थाने वापरली आहे. तसेच ‘पाणी’ हा शब्द जलीय अवस्था दर्शवितो. अशा मिश्रणात एक द्रव अखंड स्थितीत असतो व दुसरा द्रव त्यात चांगल्या तऱ्हेने अपस्कारित झालेला (विखुरलेला) असतो. पायसाचे स्थैर्य बऱ्याच अंशी स्थैर्य प्राप्त करून देणाऱ्या साबणासारख्या घटकांवर अवलंबून असते. अशा घटकांच्या रेणूंचे तेल व पाणी यांच्या आंतरपृष्ठाशी एकीकरण होते. या रेणूंच्या रचनेतील एक भाग तेलात विद्राव्य असतो व दुसरा भाग पाण्यात विद्राव्य असतो. याप्रमाणे हे रेणू आंतरपृष्ठाशी दोन द्रवातील दुव्याचे काम करतात. त्यांच्यामुळे सामान्यत: त्या दोन द्रवांमधील आंतरपृष्ठीय ताण कमी होतो. [→ पायस]. फेस निर्माण झाला असता ज्या विद्रावांचा पृष्ठताण कमी होतो अशा सर्व विद्रावांवर फेस तयार होतात. शुद्ध द्रवावर फेस अगदी थोड्या प्रमाणात तयार होतो किंवा जवळ जवळ तयार होत नाही आणि जे बुडबुडे तयार होतात ते त्वरित नाहीसे होतात. स्थैर्य प्राप्त झालेला फेस मिळविण्यासाठी पृष्ठपटल श्यान (दाट) असावयास हवे किंवा ते तसे बनवावयाला हवे. फेस तयार होण्याची पृष्ठघटना पृष्ठभाग स्वच्छ करण्याच्या बाबतीत अगत्याची आहे. अग्निशमनासाठी वापरण्यात येणारा कार्बन डाय-ऑक्साइडयुक्त फेस महत्त्वाच्या प्रकारचा आहे. अशा वेळी अर्धटिकाऊ जलीय आवरणाची जरूरी असते व त्यासाठी लागणारा फेस सोडियम बायकार्बोनेट व धातुयुक्त लवण (उदा., ॲल्युमिनियम सल्फेट) यांपासून बनवितात. [→ फेस आगनिवारण ].

थेंब व बुडबुडे यांचे उपयोग : मोटारी रंगविणे, जंतुनाशकाची फवारणी करणे अशासारख्या क्रियांमध्ये अल्प द्रवाने जास्तीत जास्त क्षेत्रफळ व्यापता यावे हा उद्देश असतो. यासाठी सूक्ष्म थेंबांच्या फवाऱ्याचा उपयोग करतात. वायुरूप माध्यमात असा फवारा मारला असता माध्यम व द्रव यांच्यात संपर्क येणारे क्षेत्रफळ वाढते. त्यामुळे वाळविणे किंवा रासायनिक विक्रिया होणे यासारख्या क्रिया जास्त कार्यक्षमतेने घडून येतात. उधा., तप्त वायूच्या प्रवाहात फळांचे रस किंवा दूध यांचे फवारे मारून ते सुकवून त्यांच्या भुकट्या बनविल्या जातात. डीझेल एंजिनात इंधनाचा फवारा मारून त्याच्या ज्वलनाची क्रिया जास्त संपूर्णपणे घडवून आणली जाते. संघटित द्रवापेक्षा त्याच्या थेंबाच्या मुक्तपृष्ठाचे क्षेत्रफळ जास्त असते. त्यामुळे द्रवाची थेंबात विभागणी होण्यासाठी पृष्ठताणाच्या प्रेरणेविरुद्ध कार्य करावे लागते व म्हणून द्रवाला जास्त दाब देणे वा वेग देणे इ. उपायांनी त्याला ऊर्जा पुरवावी लागते. प्रत्येक क्रियेसाठी थेंबांचा सुयोग्य आकार वेगळा असू शकतो. तो मिळावा यासाठी दाब, द्रवाचा वेग व फवाऱ्याच्या पंपाच्या छिद्राचा व्यास यांची निवड योग्य प्रकारे करावी लागते.

द्रव माध्यमात वायूचे बुडबुडे उत्पन्न करूनही त्या दोहोंमधील संपर्क क्षेत्रफळ वाढवता येते. द्रव उकळतो तेव्हा (उष्णता ऊर्जा पुरवून) द्रवात बुडबुड्यांची मालिकाच तयार केली जाते. सूक्ष्म छिद्रातून मोठ्या दाबाने द्रवात वायू सोडूनही बुडबुडे उत्पन्न करता येतात. बाष्पीभवन, ऊर्ध्वपातन (द्रवमिश्रणाची वाफ करून व मग ती थंड करून क्रमाक्रमाने घटक अलग करणे), प्रशीतन, शोषण इ. प्रक्रियांत बुडबुडे कार्यरत होत असतात. प्रदूषण कमी करण्यासाठी कारखान्यांच्या धुराड्यांतून किंवा मैला पाण्यातून उत्सर्जित होणारे वायू ‘शोषण स्तंभा’ तून बुडबुड्यांच्या स्वरूपात जाऊ देतात. इष्ट वायू ज्यात विद्रुत होतील अशा द्रवाचा हा स्तंभ असतो. द्रायवीकरणामध्येही बुडबुड्यांचाच उपयोग केला जातो.

पहा : पृष्ठक्रियाकारके पृष्ठविज्ञान.

संदर्भ : 1. Adamson, A. W. The Physicsl Chemistry of Surfaces, New York, 1967.

             2. Alexander, A. E. Surface Chemistry, London

             3. Davis, J. T. Rideal, E. K. Interfacial Phenomena, New York, 1963.

             4. Newman, F. H. Searl, V. H. L. The General Properities Of Matter, London, 1962.

             5. Poynting, J. H. Thomson, J. J. (Revosed by Todd, G. W.) University Textbook of Physics, Vol. 1, London, 1947.

जोशी, र. वि. पुरोहित, वा. ल.

“