नैकरेषीय आविष्कार

नैकरेषीय आविष्कार : (अरेषीय आविष्कार). भौतिकी शास्त्रात अशा अनेक राशी आहेत की, ज्यांचे परिवर्तन सामान्यतः रेषीय स्वरूपाचे आहे (म्हणजे ज्याचे इतर राशींशी असलेला संबंध दर्शविणारे समीकरण एकघाती असते किंवा या संबंधाचा आलेख सरळ रेषेच्या स्वरूपाचा आहे) असे मानले जाते पण काटेकोरपणे पाहिले असता हे चलन वस्तुतः रेषीय असत नाही. उदा., (१) वाढत्या तापमानामुळे धातूच्या दंडाच्या लांबीमध्ये होणारी वाढ, (२) स्थितिस्थापक (लावलेला ताण काढून घेतल्यानंतर मूळ स्थितीत परत येणारा) तंतू ताणला असता त्याच्या लांबीमध्ये होणारे विस्तारण ताणणारी प्रेरणा व त्यामुळे होणारे विस्तारण यांमधील संबंध हूक यांच्या नियमानुसार मिळतो, (३) विद्युत् संवाहकाकरिता लावलेले विद्युत् वर्चसांतर (विद्युत् पातळ्यांतील फरक, V) व मिळणारे विद्युत् प्रवाहाचे मूल्य (І) यांमधील संबंध ओहम यांच्या नियमाने दिला जातो. हा संबंध संवाहकाकरिता V-І अभिलक्षण वक्राने (आलेखाने) दाखविला जातो, (४) एखादा उष्ण पदार्थ त्यापेक्षा कमी तापमानाच्या वातावरणात ठेवला, तर त्याचे होणारे शीतन हे न्यूटन यांच्या शीतन नियमानुसार मिळते. भौतिकीय राशीत होणारा बदल जर फार मोठ्या मूल्याचा नसेल, तर हा बदल आसन्नपणे (जवळजवळ) रेषीय स्वरूपाचा असतो असे मानणे सोईस्कर पडते. कारण या प्रकारच्या रेषीय बदलाचे गणितीय विश्लेषण करणे सोपे असते. हे परिणाम घडवून आणणारी विक्षोभक कारके एकाहून जास्त असतील व ती एकाच वेळी कार्य करीत असतील, तर त्याकरिता अध्यारोपण तत्त्वाचा उपयोग करता येतो. प्रत्येक कारकाकरिता त्यापासून मिळणाऱ्या परिणामाचे गणन करून सर्व कारके एकाच वेळी उपयोजित केली, तर परिणामाचे मूल्य काय मिळेल हे काढणे सोपे पडते.

जास्त अचूक प्रयोग करून असे दाखविता येते की, भौतिकीमधील बहुसंख्य परिणाम नैकरेषीय आहेत. निरनिराळ्या प्रकारच्या निर्वात नलिका, अर्धसंवाहक द्विप्रस्थ [→ इलेक्ट्रॉनीय प्रयुक्ति], ⇨ थर्मिस्टर इ. प्रयुक्तींचा शोध लागल्यापासून नैकरेषीय आविष्कारांच्या अभ्यासास महत्त्व आले आहे. मापन तंत्रविद्येमध्ये झालेल्या मोठ्या सुधारणेमुळे हे कार्य शक्य झाले आहे. आधुनिक काळात असे काही नवीन आविष्कार आढळले आहेत की, ज्यांची तुलना मागे संशोधिलेल्या कोणत्याही आविष्काराशी होऊ शकत नाही. या नवीन आविष्काराचे विशदीकरण करण्याकरिता सर्वस्वी नवीन अशी भौतिकीय तत्त्वे वापरावी लागतात. ⇨ नियंत्रण प्रणाली व ⇨ ध्वनी या नोंदींमध्ये अशा काही नैकरेषीय आविष्कारांविषयी उल्लेख आलेला आहे. प्रस्तुत नोंदीत (१) नैकरेषीय विद्युत् मंडले व मंडल घटक आणि (२) नैकरेषीय प्रकाशकी या दोन आविष्कारांविषयी सविस्तर माहिती दिलेली आहे.

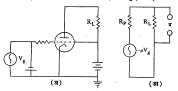
विद्युत् मंडल घटक : विद्युत् मंडलातील घटक मुख्यत्वेकरून दोन प्रकारचे असतात. (१) रोधक, धारित्र (विद्युत् भार साठविणारे साधन), प्रवर्तक (बदलत्या चुंबकीय क्षेत्रामुळे ज्यात विद्युत् चालक प्रेरणा – मंडलात विद्युत् प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा–निर्माण होते असा घटक, उदा., तारेचे वेटोळे) यांसारखे अक्रिय घटक. (२) विद्युत् घटाच्या द्वारे मिळणारी सरल विद्युत् चालक प्रेरणा व प्रत्यावर्ती (उलट सुलट दिशांनी कार्य करणारा) विद्युत् चालक उद्‌गम (प्रत्यक्ष वा समतुल्य) यांस जनित्रे किंवा सक्रिय घटक म्हणतात.

वरील मंडलात विद्युत् वर्चस् हे आदान होते, तर त्यापासून मंडलात मिळणाऱ्या विद्युत् प्रवाहास प्रदान म्हणतात. सक्रिय जनित्र असल्याशिवाय मंडलात विद्युत् प्रवाह मिळणार नाही हे उघड आहे. निर्वात त्रिप्रस्थनलिकेला अथवा ट्रँझिस्टरला आदान संकेत दिला असता याचा परिणाम म्हणून त्याच्या प्रदान मंडलात समतुल्य विद्युत् वर्चस् अथवा विद्युत् प्रवाह जनित्र निर्माण होते असे मानून गणन करता येते. रोध भार असलेल्या त्रिप्रस्थ नलिका विवर्धकाकरिता [→ इलेक्ट्रॉनीय विवर्धक] समतुल्य जनित्र कसे घेतले जाते हे आ.१ वरून दिसून येईल. बऱ्याच अक्रिय मंडल घटकांची वर्तणूक त्यावर लावलेल्या जनित्राच्या विद्युत् वर्चसाच्या स्वरूपावर अवलंबून राहते असे दिसते. सर्वसाधारणपणे (१) सरल, (२) ज्या–वक्रीय (म्हणजे त्रिकोणमितीतील ज्या गुणोत्तराच्या आलेखासारखे) प्रत्यावर्ती, (३) कालपरिवर्ती (कालानुसार बदलणारे) उदा., करवती अथवा चौरसाकृती तरंगाकाराचे किंवा स्पंद स्वरूपी व (४) पायरी फलन (पायरीच्या स्वरूपाचा आलेख येणारे) या प्रकारचे विद्युत् वर्चस् प्रयोगशाळेत आढळतात. यांपैकी प्रकार १, २ व ४ हे विशेष महत्त्वाचे आहेत.

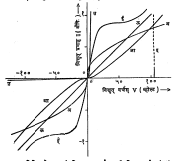
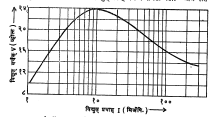
एखादा घटक किंवा मंडल रेषीय आहे की नाही हे ठरविण्याकरिता त्याला निरनिराळे आदान (विद्युत् वर्चस्) देऊन त्यातून मिळणारे तदनुरूप प्रदान (विद्युत् प्रवाह) मोजले जाते. सरल विद्युत् वर्चसाकरिता काही रोधांसाठी मिळणारे अभिलक्षण V-I वक्र आ. २ मध्ये दाखविले आहेत.

टंगस्टन तंतूकरिता मिळणाऱ्या वक्रासारखा वक्र सर्वसाधारणपणे सर्व शुद्ध धातूंकरिता मिळतो. अशा संवाहकाचा रोध निरपेक्ष तापमानाच्या रेषीय प्रमाणात वाढतो. या प्रकारचा दिवा जेव्हा प्रकाश देत असतो तेव्हाचा त्याचा रोध, त्याच्या कोठी तापमानाच्या (सर्वसाधारण तापमानाच्या) रोधापेक्षा साधारणपणे १० पटींनी जास्त असतो. ज्या घटकाकरिता रोध वाढत्या तापमानाबरोबर वाढत जातो त्याचा अभिलक्षण वक्र धन स्वरूपाचा आहे असे म्हणतात. (आ) या वक्रात दाखविलेले कार्बन तंतूच्या दिव्याकरिता मिळणारे चलन याच्या उलट आहे. या घटकाकरिता रोधताप गुणांक (घटकाच्या तापमानात एक अंश से. बदल झाल्यास त्याच्या रोधामध्ये होणारा बदल आणि ०^° से. ला असणारा त्याचा रोध यांचे गुणोत्तर) ऋण स्वरूपाचा आहे असे दिसते. आयर्न ऑक्साइडाच्या थर्मिस्टराकरिता अशाच प्रकारचे चलन काही भागात मिळते (आ. ३).

---

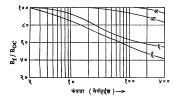
आ.४ मध्ये सिलिकॉन कार्बाइड व्हेरिस्टराकरिता दाखविलेला वक्र हाच आविष्कार दाखवितो.

आ.२ मध्ये एकदिशकारकांकरिता (प्रत्यावर्ती विद्युत् प्रवाहाचे एकाच दिशेने वाहणाऱ्या प्रवाहात रूपांतर करणाऱ्या साधनाकरिता) दाखविलेला (उ) हा वक्र एक निराळ्याच तऱ्हेची नैकरेषीयता दाखवतो. यामध्ये विद्युत् वर्चसाच्या एका दिशेकरिता रोध कमी असतो, तर त्याच्या उलट दिशेने वर्चस् लावले असता त्याचा रोध प्रचंड असल्यामुळे या स्थितीत मिळणारा विद्युत् प्रवाह नगण्य मानता येतो.

आ. २ मधील (ऊ) हा वक्र रेडिओ मंडलामध्ये वापरण्यात येणाऱ्या काटेकोर रोधकाकरिता मिळालेला आहे.

वरील वक्रांपेक्षा जास्त जटिल (गुंतागुंतीच्या) तऱ्हेचे फेरबदल आ. ५ व आ. ६ मध्ये अनुक्रमे मंदतेज प्रज्योत विद्युत् विसर्जन व चतुर्प्रस्थ निर्वात नलिका यांकरिता मिळतात.

या व इतर नैकरेषीय वक्रांवरून असे दिसते की, घटकाचा रोध त्याच्या कार्यकारी बिंदूवर (लावलेल्या वर्चसाने निश्चित केलेला) अवलंबून असतो. याकरिता अल्पबदली रोध (R_AC) ही राशी वापरणे जास्त सुयोग्य ठरते. R_AC=dV/DI येथे या अवकल समीकरणाने [→ अवकल समीकरणे] दिला जातो. कोणत्याही घटकाचा सरल विद्युत् वर्चसाकरिता असणारा रोध R_DC व अल्पबदली रोध R_AC यांमध्ये सर्वसामान्यपणे फरक राहतो. R_AC हा रोध विद्युत् वर्चस् जेव्हा कालपरिवर्ती असेल तेव्हा वापरणे आवश्यक ठरते.

सरल विद्युत् वर्चसाकरिता ओहम नियमाप्रमाणे घटकामध्ये होणारे विद्युत् ऊर्जेचे अपचयन (लय होणे) हे R_DCया रोधमूल्यामुळे ठरते. जेव्हा वर्चस् कालपरिवर्ती असते तेव्हा हे अपचयन दुसऱ्या अनेक कारणांमुळे होऊ शकते. यामध्ये (१) आवर्त प्रवाहामुळे (चुंबकीय स्त्रोतात बदल झाल्याने संवाहकातच प्रवर्तित झालेल्या प्रवाहामुळे), (२) चुंबकीय पदार्थामधील मंदायन परिणामामुळे [→ चुंबकत्व], (३) निरोधकामधील विद्युत् अपारकातील (ज्यातून विद्युत् प्रवाह वाहू शकत नाही अशा पदार्थातील) ऊर्जा व्ययामुळे अपचयनास मदत होते.

रेषीयतेकरिता दिलेली सर्वग्राही व्याख्या अशा कालपरिवर्ती वर्चसाकरिता सुद्धा यथार्थ राहते असे मानले जाते. या व्याख्येप्रमाणे रेषीय घटकाकरिता प्रदान/आदान हे गुणोत्तर वर्चसाचा (१) परमप्रसर (स्थिर स्थितीपासून होणारे कमाल स्थानांतरण), (२) कंप्रता (एका सेकंदात होणाऱ्या कंपनांची संख्या) अथवा कला (एखाद्या स्वेच्छ स्थितीच्या संदर्भात असणारे कोनात मोजण्यात येणारे अंतर) यांपैकी कोणत्याही राशीवर अवलंबून नसले पाहिजे. असे झाले तरच आदान आणि प्रदान वर्चस् तरंगाकार एकाच स्वरूपाचे राहतील व घटक किंवा मंडल वापरल्यामुळे चल (बदलणारा) विलंब (आदान लावलेल्या क्षणापासून प्रदान मिळेपर्यंत लागणारा कालविलंब) आदी प्रकारही आढळणार नाहीत. सरल विद्युत् वर्चसाकरिता जे मंडल घटक बऱ्याच प्रमाणात रेषीय वर्तणूक दाखवितात ते कालपरिवर्ती वर्चसाकरिता साधारणपणे तशीच वर्तणूक दाखवतील, ही अपेक्षा खरी ठरत नाही. विविध प्रकारच्या परिणामांमुळे या घटकाच्या विद्युत् राशीमध्ये वर्चस् कंप्रतेबरोबर फेरबदल होतात असे आढळते. आ. ७ मध्ये भरीव संवाहकाचा रोध वर्चसाच्या कंप्रतेनुसार कसा बदलतो हे दाखविले आहे. हा फरक ⇨ त्वक् परिणामा मुळे होतो. या परिणामानुसार विद्युत् प्रवाहाची कंप्रता वाढविली असता भरीव संवाहकामधील विद्युत् प्रवाहाचे संवहन अधिकांशाने पृष्ठभागाजवळील थरामधून होऊ लागते.

आ. ८ मध्ये रेडिओ मंडलात वापरण्यात येणाऱ्या कार्बन रोधकाचा रोध कंप्रता बदलली असता कितपत बदलतो हे दाखविले आहे.

निरोधक हासुद्धा एक नैकरेषीय घटक आहे. जोपर्यंत लावलेले विद्युत् वर्चस् एका ठराविक मर्यादेच्यापेक्षा कमी असते तोपर्यंत निरोधकामधून वाहणारा विद्युत् प्रवाह नगण्य असतो पण विद्युत् वर्चसाचे मूल्य या ठाराविक सीमेपलीकडे नेले, तर तो निरोधक विद्युत् प्रवाहाचे संवहन करू शकतो. याचे हवा हे उत्तम उदाहरण आहे. हवा सामान्य विद्युत् वर्चसाकरिता निरोधक म्हणून कार्य करते पण उच्च व्होल्ट दाबाची तडित् तीमधून  सहज जाऊ शकते. विद्युत् वर्चस् संवेदनशील प्रयुक्तीचे हे एक उदाहरण आहे.

या सर्व आविष्कारांचा अंतर्भाव मंडल विश्लेषणामध्ये कसा केला जातो, याचे वर्णन इतर घटकांमधील नैकरेषीय आविष्काराच्या वर्णनानंतर केले आहे.

---

धारित्र : निरनिराळे विद्युत् वर्चस् असलेल्या संवाहकांमध्ये निरोधक माध्यम ठेवले असता त्यामुळे धारित्र तयार होते. यामध्ये स्थैतिक विद्युत् ऊर्जेचा संचय केला जातो. जर संवाहकावर असलेला संपूर्ण विद्युत् भार q, संवाहकामधील विद्युत् वर्चसांतर V असेल, तर धारित्राची धारणक्षमता C = q/v या सूत्राने मिळते.  q आणि V या राशींतील चलन रेषीय नसेल, तर अल्पबदली धारणक्षमतेचे मूल्य C_AC = dq/dv या समीकरणाने मिळते. विद्युत् वर्चस् उद्‌गमास जोडून धारित्र विद्युत् भारित केले जाते. तेव्हा मिळणारा अस्थिर विद्युत् प्रवाह i = C dV/dt या सूत्राने मिळतो. धारित्रामध्ये निरोधक असल्यामुळे ते सरल विद्युत् वर्चस् उद्‌गमाला जोडले असता विद्युत् मंडल पूर्ण होत नाही व त्यामुळे त्यात अखंडित वाहणारा विद्युत् प्रवाह मिळत नाही हे उघड आहे. धारित्र भारित झाल्यावर यामध्ये भाराचा जो संचय होतो त्यामुळे त्यात  ½CV² = ½qV एवढ्या स्थैतिक विद्युत् ऊर्जेचा संचय केला जातो. विद्युत् ऊर्जा संचयाचा हा प्रकार विद्युत् वर्चस् अथवा व्होल्टेज या तऱ्हेचा असतो असे दाखविता येते.

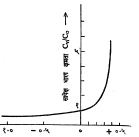सिलिकॉन (अथवा तत्सम अर्धसंवाहक) द्विप्रस्थाच्या संधी भागात पर्यावेश (इलेक्ट्रॉन किंवा पोकळ्या यांचा स्थिर संचय) जमतो व त्यामुळे अवरोध धारित्र परिणाम मिळतो. धारित्राच्या व्याख्येंचे व्यापकीकरण केल्यास ज्या ठिकाणी स्थैतिक विद्युत् ऊर्जेचा (विद्युत् भार अथवा वर्चस् याच्या स्वरूपात) संचय होतो त्यास धारणक्षमता आहे, असे म्हणता येते. यामुळे द्विप्रस्थाच्या संधी भागात काही १०^-१२ फॅराड एवढी धारणक्षमता असलेले नैकरेषीय धारित्र मिळते (आ. ९). अशा धारित्राची धारणक्षमता C पुढील सूत्राने मिळते. C = AV^-1/2 येथे V त्यावरील विद्युत् वर्चसांतर व A स्थिरांक. समांतर पट्टिका धारित्राची धारणक्षमता ही बऱ्याच अचूकतेने खालील सूत्राने मिळते.

C = Aε_o /d

येथे A पट्टिकेचे क्षेत्रफळ,  d त्यांमधील अंतर आणि Є_O निरोधकाची अपार्यता (सयुक्तिक एम. के. एस. पद्धतीप्रमाणे).

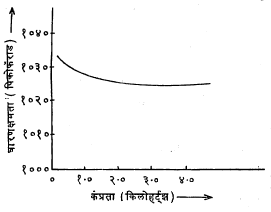यांपैकी निरोधकाची अपार्यता ही त्याच्या तापमानावर व विद्युत् वर्चसाच्या कंप्रतेवर अवलंबून असल्यामुळे या धारित्राच्या धारणक्षमतेने या दोन राशींप्रमाणे बदल दाखवावा हे अपेक्षित आहे. आ.१० मध्ये टेफ्लॉन, स्टायरीन आणि मायलर या निरोधक म्हणून उच्च प्रतीच्या धारित्राकरिता उपयोगात असलेल्या प्लॅस्टिक पदार्थाच्या धारित्राच्या धारणक्षमतेत वाढत्या तापमानाबरोबर होणारा बदल दाखविला आहे. आ.११ मध्ये धारित्राच्या धारणक्षमतेत कंप्रतेनुसार होणारा फरक दाखविला आहे. अति-उच्च कंप्रतेच्या संकेताकरिता त्यामुळे उत्पन्न होणाऱ्या चुंबकीय क्षेत्रामुळे सुद्धा परिणामी धारणक्षमतेत फरक पडतो. आदर्श धारित्रामध्ये विद्युत् ऊर्जेचे अपचयन शून्य असते असे सिद्ध करता येते पण प्रत्यक्षातील सर्व धारित्रांमध्ये अपचयन आढळतेच. हा व इतर काही परिणाम लक्षात घेण्याकरिता हवा निरोधक असलेल्या धारित्राकरिता आ. १२ मध्ये दाखवलेले समतुल्य मंडल गृहीत धरतात.

---

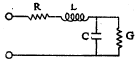
काही मंडल घटक व्यक्तीशः रेषीय असले, तरी अशा अनेक घटकांची मांडणी करून मिळविलेले मंडल रेषीय असतेच असे नाही (पहा : पृ. ९५७, २ रा परिच्छेद). या कारणाकरिता प्रत्यक्षातील धारित्राचे समतुल्य मंडल वर देण्यात आले आहे [→विद्युत् धारित्र].

प्रवर्तक : संवाहकातून विद्युत् प्रवाह पाठविला असता त्याच्या सभोवती चुंबकीय क्षेत्र निर्माण होते. या चुंबकीय क्षेत्रनिर्मितीमुळे एक ठराविक चुंबकीय स्त्रोत संवाहकाशी संलग्न होतो. संलग्न स्त्रोताचे मूल्य N व संवाहकातील विद्युत् प्रवाह i एवढा असेल, तर संवाहकाची प्रवर्तकता L ही L = N/i या सूत्राने मिळते. सरळ संवाहक तारेच्या ऐवजी तिचे वेटोळे केले, तर संलग्न स्त्रोताचे मूल्य वाढून प्रवर्तकता वाढते.

लोखंड किंवा तत्सम इतर लोहचुंबकीय पदार्थाच्या (उदा., फेराइट) गाभ्याभोवती जर विद्युत् प्रवाह वाहक वेटोळी गुंडाळली, तर त्याच्या प्रवर्तकतेत खूप वाढ होते व त्यांना इष्ट असे अनेक गुणधर्म प्राप्त होतात. प्रवर्तकतेत होणारी अशी वाढ १००–१,००० पटींची असते. गाभ्याच्या मंदायन व संपृक्तता या इतर परिणामामुळे लोखंडी गाभायुक्त प्रवर्तकाकरिता N व i या राशींचे एकमेकींबरोबरचे चलन आ.१३ मध्ये दाखविल्याप्रमाणे नैकरेषीय स्वरूपाचे होते. इतर राशींप्रमाणे अल्पबदली (अथवा प्रत्यावर्ती) प्रवर्तकतेचे मूल्य L_AC = dN/di या सूत्राने मिळते. आ.१३ मध्ये L_AC चे विद्युत् प्रवाहाबरोबर होणारे चलन वक्र (आ) मध्ये दाखविले आहे. लोखंडाचा गाभा असलेल्या प्रवर्तकाकरिता चुंबकीय स्त्रोत N व विद्युत् प्रवाह i यांमधील संबंध खालील सूत्राने मिळतो, असे सामान्यपणे मानले जाते.

i = aN + bN³

येथे a आणि b हे स्थिरांक आहेत.

धारित्राप्रमाणे प्रवर्तक विद्युत् ऊर्जेचा संचय करू शकतो. ही ऊर्जा चुंबकीय स्वरूपाची असल्यामुळे ही संचय पद्धती विद्युत् प्रवाहावर अवलंबून असलेल्या प्रकारची असली पाहिजे हे स्पष्ट आहे. हिचे मूल्य ½Li₀² या सूत्राने मिळते. येथे L हे प्रवर्तकत्व व i₀ हे विद्युत् प्रवाहाचे अंतिम स्थिर मूल्य आहे. संवाहक वेटोळ्यापासून बनविलेल्या प्रवर्तकास काही प्रमाणात रोध व काही प्रमाणात धारणक्षमता असते. या कारणाकरिता या प्रकारच्या प्रवर्तकाकरिता समतुल्य मंडल आ.१४ (आ) मध्ये दाखविल्याप्रमाणे असते. वेटोळ्याची प्रवर्तकता कंप्रता वाढविल्यास (≈ ४ किलोहर्ट‌्झ) जवळजवळ ७ % कमी होते. ही घट वेटोळ्याच्या निरोधकी रोधावर (R₁) अवलंबून राहते. नवीन प्रवर्तकता L_f ही खालील सूत्राने मिळते.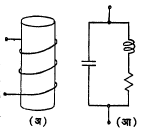

Lf =	L
	1+(2pfL/ R1)2

येथे L = प्राथमिक प्रवर्तकता , f = कंप्रता. त्वक् परिणामामुळे सुद्धा प्रवर्तकतेत घट होते. हिचा समावेश वरील घटीत केला गेलेला नाही.

---

विद्युत् मंडले : विद्युत् मंडलात रोधक, प्रवर्तक व धारित्र यांसारखे अक्रिय घटक एका ठराविक आकृतिबंधात मांडले असून ते एकमेकांबरोबर शून्य रोध, धारणक्षमता व प्रवर्तकता असलेल्या जोडपथांनी संलग्न केलेले असतात. या मंडलाकरिता चालक म्हणून एक किंवा अधिक प्रत्यक्ष जनित्रे असतात. त्यांमध्ये निर्वात नलिका, ट्रँझिस्टर अशा सक्रिय प्रयुक्ती असतील, तर त्यांचे निदर्शन समतुल्य मंडले वापरून केले जाते. या समतुल्य निदर्शनात विद्युत् प्रवाह अथवा विद्युत् वर्चस् जनित्र असे सक्रिय विभाग व त्याबरोबरच काही अक्रिय घटकांचा समावेश केला जातो. विद्युत् मंडलाकरिता बहुतांशी विद्युत् वर्चस् हे आदान असते, तर त्यापासून मिळणारा विद्युत् प्रवाह हा प्रदान असतो. काही वेळा प्रदान हे सुद्धा विद्युत् वर्चस् असू शकते (उदा., इलेक्ट्रॉनीय विवर्धक).

ज्या मंडलाकरिता प्रदान/आदान हे गुणोत्तर (म्हणेजच स्थानांतरण फलन) हे आदान संकेताच्या परमप्रसर, कंप्रता इ. कोणत्याही विशिष्ट राशीवर जर अवलंबून नसेल, तर ते मंडल रेषीय आहे असे समजले जाते. नैकरेषीय मंडलाकरिता स्थानांतरण फलन आदान वर्चसाचा परमप्रसर, कंप्रता किंवा कला यांप्रमाणे बदलते. जर मंडलात धारित्र व प्रवर्तक यांसारखे ऊर्जा संचायक असतील किंवा त्यामध्ये निर्वात नलिका, ट्रँझिस्टर यांसारखे सक्रिय घटक असतील आणि चालक विद्युत् वर्चस् कालपरिवर्ती असेल, तर या मंडलाच्या स्थैतिक अभिलक्षण वक्रावरून मंडल रेषीय किंवा नैकरेषीय आहे, हे ठरवता येत नाही. मंडलाची नैकरेषीयता ही त्यामध्ये वापरलेल्या घटकांच्या नैकरेषीयतेवर अवलंबून असते. काही वेळा हे घटक आसन्नपणे रेषीय असले, तरी त्यांची मांडणी अशा प्रकारे असू शकते की, त्यापासून मिळणारे मंडल नैकरेषीय असते. हा प्रकार विशेषतः ज्यामध्ये पुनःप्रदाय योजना (प्रदान संकेतापैकी काही भाग आदान संकेत होण्याची योजना) वापरलेली असते अशा इलेक्ट्रॉनीय मंडलात आढळतो. उदा., स्विचिंग मंडले. या मंडलांना पूर्णपणे स्थिर अथवा तात्पुरती स्थिर अशा दोनच अवस्था असतात.

सर्वसाधारणपणे मंडलाच्या वर्तणुकीचे वर्णन करण्याकरिता जी. आर्. किरखोफ यांच्या नियमांपैकी [→ एकदिश विद्युत् प्रवाह] कोणत्याही एका नियमाचा उपयोग करून एक अवकल समीकरण मांडता येते. मंडल जर रेषीय असेल, तर त्याचे नियंत्रण करणारे अवकल समीकरण रेषीयच असते. रेषीय समीकरण सोडविण्याकरिता निरनिराळ्या पद्धती उपलब्ध आहे. जर मंडल नैकरेषीय असेल, तर तद्नुरूप अवकल समीकरण सुद्धा नैकरेषीय असते. याकरिता चार प्रकारच्या पद्धती वापरल्या जातात. (१) काही थोड्या नैकरेषीय समीकरणांचे सम्यक निर्वाह (उत्तरे) काढणे शक्य असते. (२) नैकरेषीय मंडलाकरिता (इष्ट कार्यपल्ल्याकरिता) एक समतुल्य रेषीय मंडल गृहीत धरणे. (३) विभाग मर्यादित रेषीयकरण : या पद्धतीत वक्र स्थानांतरण फलनाचे एकापेक्षा अधिक असे रेषीय विभाग पाडून प्रत्येक विभागाकरिता फक्त यथार्थ अशी समतुल्य रेषीय मंडले गृहीत धरणे. (४) आलेखी विश्लेषण पद्धती. या कार्याकरिता संगणकाचा (गणितकृत्ये करणाऱ्या यंत्राचा) वापर मोठ्या प्रमाणात केला जातो. या पद्धतींचा प्रत्यक्षात कसा उपयोग केला जातो हे दाखविण्याकरिता काही उदाहरणे खाली दिली आहेत.

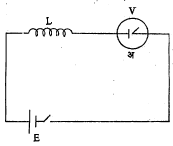पर्यावेश नियंत्रित निर्वात द्विप्रस्थ व प्रवर्तक यांमध्ये विद्युत् प्रवाहाची वाढ : (पायरी फलन विद्युत् वर्चस्). अ हा निर्वात द्विप्रस्थ असून मंडलाला E विद्युत् वर्चस् लावले असता त्यावरील t = 0 या क्षणी V एवढे विद्युत् वर्चस् आहे असे समजले आहे. मंडलाचा प्रतिसाद लावलेल्या विद्युत् वर्चसाच्या प्रकारावर अवलंबून असतो याचा उल्लेख मागे आला आहे. प्रस्तुत उदाहरणातील विद्युत् वर्चस् पायरी फलन आकाराचे आहे. याचे मूल्य t &lt 0 करिता शून्य आहे व t = 0 आणि t &gt 0 करिता स्थिर व सरल असे विद्युत् वर्चस् कार्य करते.

द्विप्रस्थाकरिता विद्युत् प्रवाह i = k V^3/2

येथे k हा स्थिरांक आहे. या मंडलाकरिता खालील अवकल समीकरणाची पूर्तता होते.

L	di	+ V = E
	dt
V+L		d	(kV3/2) = E
		dt

जर t = 0 या क्षणी i = 0,  V = 0 असेल तर वरील समीकरणाचानिर्वाह √E. tan h^-1 ( √ (V/E) ) – √ V =  t / 3KL हा आहे असे दाखविता येते.

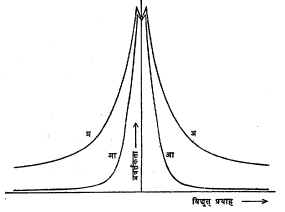
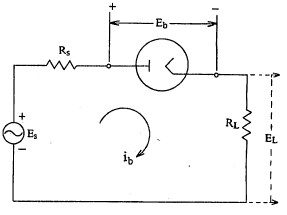प्रत्यावर्ती विद्युत् वर्चस् उद्‌गमाकरिता एकदिशकारकातून वाहणारा प्रवाह व भार रोधावर मिळणारे प्रदान : (प्रत्यावर्ती विद्युत् वर्चस् स्थिर स्थिती प्रतिसाद). उदाहरणादाखल घेतलेले प्रत्यक्ष मंडल आ.१६ मध्ये दाखविले आहे. E_S हे प्रत्यावर्ती विद्युत् वर्चस् आहे आणि त्याचे मूल्यE_S = E_OS sin wt या सूत्राने मिळते. येथे E_OS हे प्रत्यावर्ती विद्युत् वर्चसाचे शिखर मूल्य असून ω/2^π ही कंप्रता आहे. त्याचा आंतरिक रोध R_S एवढा आहे. R_L हा भार रोध असून त्यावरील प्रदान E_L एवढे आहे. कोणत्याही एका क्षणी एकदिशकारकावरील विद्युत् वर्चसांतर E_b आहे व i_b या मूल्याचा विद्युत् प्रवाह वलयातून याक्षणी वाहतो असे गृहीत धरले आहे. जर एकदिशकारक निर्वात प्रकारचा असून त्यामधील विद्युत् प्रवाह पर्यावेश नियंत्रित आहे असे मानले, तर 

i_b = kE_b^3/2

 वलयाला किरखोफ नियम लावला असता

( R_S +R_L ) i_b + ( i_b/k)^2/3 = E_S = E_OS sinωt…. (१)

हे समीकरण मिळते. याचा निर्वाह काढून कोणत्याही क्षणी वलयातील विद्युत् प्रवाह i_b व त्यामुळे भारावरील प्रदान विद्युत् वर्चस् यांची मूल्ये काढणे हे विश्लेषणाचे उद्दिष्ट असते. (१) या समीकरणाचा निर्वाह काढणे तितके सोपे नाही. याकरिता खाली वर्णन केलेली विभाग मर्यादित रेषीयकरणाची पद्धत आपण वापरू शकतो.

---

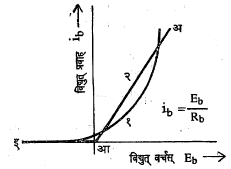विभाग मर्यादित रेषीयकरण : आ.१७ मध्ये एकदिशकारकाचा प्रत्यक्ष स्थैतिक अभिलक्षण वक्र (१) दाखविला आहे. हा अआ आणि आइ या दोन रेषीय विभागांबरोबर सममुल्य आहे असे या पद्धतीत मानले जाते. E_b धन असले म्हणजे एकदिशकारक प्रवाहाचे संवहन करतो व या परिस्थितीत तो R_b रोध असलेल्या रेषीय घटकाप्रमाणे वागतो. E_b जेव्हा ऋण असते तेव्हा प्रवाहाचे संवहन होत नाही.त्यामुळे या परिस्थितीत i_b = 0 असतो. वर्चसाच्या धन आवर्तनाकरिता आ.१८ मध्ये दाखविलेले समतुल्य मंडल गृहीत धरता येते.या मंडलावरून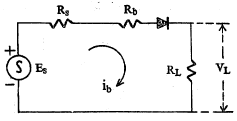

ib	=	Es
		Rs+ RL+Rb
VL	=	Es	X RL
		Rs+ RL+Rb

ही सूत्रे E_S च्या धन मूल्याकरिता मिळतात. E_S जेव्हा ऋण असेल तेव्हा i_b = 0 = V_L. प्रत्यक्ष मंडलाऐवजी त्याला अनुरूप असे विभाग रेषीयकरण केलेले मंडल गृहीत धरून आलेले परिणाम प्रत्यक्ष प्रयोगाने मिळालेल्या परिणामाशी काटेकोर जुळणार नाहीत. व्यक्तिगत नलिकेचे अभिलक्षण वक्र नलिका नियम पुस्तिकेत (मॅन्युअलमध्ये) दिलेल्या वक्राशी अगदी बरोबर जुळतातच असे नाही, ही गोष्ट या संदर्भात लक्षात घेण्यासारखी आहे. इलेक्ट्रॉनीय मंडलाच्या अभिकल्पनाकरिता (आराखडा तयार करण्याकरिता) क्षम्य त्रुटीचे प्रमाण जास्त असते. या मर्यादेत वरील पद्धत पुरेसे अचूक असे परिणाम देऊ शकते.

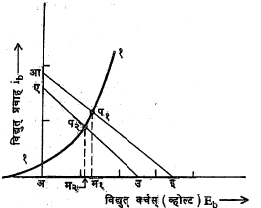
आलेखीय विश्लेषण : आ. १९ मध्ये द्विप्रस्थाचा नैकरेषीय आलेख (१) ने दाखविला आहे. गणितीय दृष्ट्या याचे निदर्शन

i_b = f (E_b)   …        …       …      …      …            (२)

या समीकरणाने करता येते. येथे f हे विशिष्ट फलन आहे. i_bव E_b यांमध्ये दुसरा एक संबंध आहे आणि हा

E_S – E_b = ( R_S + R_L) i_b …      …    ……   …. (३)

या समीकरणाने दाखविला जातो. 

समी. (३) करिता जेव्हा i_b = 0 तेव्हा E_S = E_b आणि

जेव्हा E_b = 0 तेव्हा

ib	=	Es	=	ib०
		Rs+ RL

(३) या समीकरणाचे निदर्शन -1 / R_S + R_L ही प्रवणता (उतार) असलेल्या एका रेषेने करता येते. या रेषेला भाररेषा म्हणतात. कोणत्याही क्षणी E_S, R_S, R_L यांची मूल्ये माहीत असून त्यावरून i_b व V_L चे मूल्य काढावयाचे असल्यास त्याकरिता क्ष-अक्षावर अइ = E_S व य-अक्षावर अआ = i_bo या दोन बिंदूंतून रेषा काढली जोते. i_b या राशीला एकाच वेळी समी. (२) व (३) यांची पूर्तता करावी लागते. त्यामुळे अइ = E_S एवढे विद्युत् वर्चसांतर असते तेव्हा इआ व वक्र (१) याच्या छेदबिंदूपासून लंब प_१ म_१ काढला असता त्यावरून त्याकरिता मिळणारे i_b चे मूल्य मिळते. काही काळानंतर E_S चे मूल्य कालपरिवर्ती गुणामुळे बदलून अउ एवढे झाले, तर हीच रीत वापरून या स्थितीकरिता i_b चे मूल्य प_२म_२ वरून मिळले. अशा रीतीने निरनिराळ्या भाररेषा काढून i_b ची आवश्यक क्रमिक मूल्ये काढता येतात.

नैकरेषीय प्रकाशकी : सर्वसामान्य परिस्थितीत प्रारण (तरंगरूपी ऊर्जा) व द्रव्य यांमधील परस्परक्रिया रेषीय स्वरूपाच्या असतात. याचा अर्थ द्रव्यातील अणू किंवा रेणू यांचा प्रारणामधील विद्युत् व चुंबकीय क्षेत्रांना मिळणारा प्रतिसाद रेषीय स्वरूपाचा असतो असे मानता येते. यामुळे रेषीय प्रकाशकीमध्ये प्रकाशासारखे प्रारण द्रव्यातून प्रगत होते तेव्हा त्याचा त्यामधील प्रसारण वेग, शोषण गुणांक इ. हे फक्त प्रकाशाच्या तरंगलांबीवर अवलंबून राहतात पण ते प्रकाशाच्या तीव्रतेबरोबर चलन दाखवीत नाहीत. परिणाम रेषीय मानल्यामुळे दोन किंवा अधिक तरंग एकाच वेळी द्रव्यातून प्रगत होत असतील, तर त्याचा संयुक्त परिणाम काढण्याकरिता अध्यारोपण तत्त्वाचा उपयोग करता येतो. वर वर्णन केलेल्या तत्त्वाचा उपयोग करून द्रव्याच्या पृष्ठभागापासून होणारे परावर्तन, त्याच्या आत मिळणारे प्रणमन (एका माध्यामातून दुसऱ्या माध्यमात शिरताना होणारा दिशेतील बदल), त्यामुळे होणारे व्यतिकरण (दोन तरंगमालिका एकमेकींवर येऊन पडल्यामुळे निर्माण होणारा आविष्कार) याचे विशदीकरण करता येते. ज्या परिस्थितीत द्रव्याचा विद्युत् व चुंबकीय क्षेत्रांना मिळणारा प्रतिसाद नैकरेषीय असतो, त्या परिस्थितीत द्रव्य व प्रारण यांच्या परस्परक्रियेमुळे सर्वस्वी भिन्न असे आविष्कार मिळतात. अशा आविष्कारांचा अभ्यास नैकरेषीय प्रकाशकीमध्ये केला जातो. काही घन, द्रव अथवा वायू पदार्थांच्या नैकरेषीय वर्तणुकीमुळे विशेष कुतूहल जागृत करणारे आविष्कार प्रयोगान्ती मिळतात. बेरियम सोडियम नायोबेट स्फटिकाच्या द्वारे अवरक्त (वर्णपटातील तांबड्या रंगाच्या अलीकडील अदृश्य स्वरूपातील) लेसर शलाकेचे हिरव्या रंगाच्या लेसर शलाकेत होणारे परिवर्तन [→ लेसर] हा नैकरेषीय प्रकाशकीमधील एक चित्ताकर्षक आविष्कार आहे.

---

प्रकाश प्रारणातील विद्युत् क्षेत्र १०^५– १०^६ व्होल्ट/सेंमी. या प्रमाणाचे असल्यास त्यापासून मिळणाऱ्या नैकरेषीय आविष्काराचे सुलभतेने निरीक्षण करता येते. १५० मेगॅवॉट ऊर्जेच्या रूबी लेसरपासून मिळणारी शलाका १०^–३ (मिमी.)^२ एवढ्या क्षेत्रफळावर केंद्रित केली असता त्यापासून मिळणारे क्षेत्र १०^७– १०^८ व्होल्ट/सेंमी. या दर्जाचे असते. यावरून या आविष्काराचे संशोधन करण्याकरिता लेसर शलाकेचाच उपयोग होऊ शकेल हे स्पष्ट आहे. ऐतिहासिक दृष्ट्या जरी अशा आविष्काराचा शोध लेसरच्या शोधाच्या आधी लागला असला, तरी त्यावरील संशोधनास खरी चालना लेसरच्या शोधानंतरच मिळाली. या प्रकारच्या प्रयोगाकरिता वापरलेल्या प्रकाशात उच्च तऱ्हेची एकवर्णता व दिश्यता आवश्यक असतात आणि हे गुणधर्म फक्त लेसर शलाकेतच मिळतात.

द्वितीय व उच्च प्रगुण कंप्रतेच्या कंपनांची निर्मिती : पी.ए. फ्रँकेन व त्यांचे सहाध्यायी यांनी १९६१ मध्ये प्रथम प्रयोगाद्वारे प्रकाशामध्ये उच्च प्रगुण कंप्रतेची कंपने (मूलभूत कंप्रतेच्या पूर्णांकी पटीत ज्यांची कंप्रता आहे अशी कंपने) निर्माण करता येतात हे दाखविले. रूबी लेसरपासून मिळणारे प्रकाश स्पंद विशिष्ट दिक्‌विन्यास (अक्षांच्या दिशांची अवकाशातील मांडणी) असलेल्या क्वॉर्ट्‌झ स्फटिकामध्ये केंद्रित करण्यात आले. आपाती लेसर प्रकाशाची तरंगलांबी ६३४३Å एवढी होती, तर स्फटिकातून बाहेर येणाऱ्या प्रकाशात ३४७२Å तरंगलांबीचा घटक मिळाला.

कोणत्याही पदार्थाच्या अणू किंवा रेणूवर विद्युत् क्षेत्र लावले असता त्याचे प्रवर्तित अथवा इतर प्रकारच्या विद्युत् द्विध्रुवात (परस्परांत अत्यल्प अंतर असलेल्या दोन समान व विरुद्ध विद्युत् भारांमध्ये) रूपांतर होते. या द्विध्रुवावर क्षेत्रामुळे प्रेरणायुग्मे कार्य करून त्याच्या विद्युत् परिबलाची (विद्युत् भार व त्यांतील अंतर यांच्या गुणाकाराने निर्देशित होणाऱ्या राशीची) दिशा क्षेत्राला जास्तीत जास्त समांतर करण्याचा प्रयत्न करतात. चुंबकीकरणाच्या सदृश अशीच विद्युत् ध्रुवीकरण क्रिया होते. विशदीकरण सुलभ करण्याकरिता ध्रुवीकरण (विद्युत् परिबल प्रती एकक घनफळ) P व लावलेले विद्युत् क्षेत्र E यांमध्ये एकमितीय, नैकरेषीय संबंध आहे व जो खालील श्रेढीद्वारे दाखविता येतो असे मानले, तर

P = a₁E + a₂ E² + a₃ E³ +  . . .

येथे a₁, a₂, a₃,….. स्थिरांक आहेत. 

आपाती प्रकाश शलाकेमुळे पदार्थावर पडणारे दोलायमान क्षेत्र

E = E₀ sin wt

 असेल, तर त्यामुळे ध्रुवीकरण होईल व तिचे मूल्य खालील असेल.

Pw =  a₁ E₀ sin wt + a₂ E_o² sin² wt + …

    =  a₁ E₀ sin wt + a₂/2 E₀² (1–cos·2wt) + …

यांपैकी दुसऱ्या पदामुळे दुसरा प्रगुण तर तिसऱ्या पदामुळे तिसरा प्रगुण मिळतो असे दिसते. वरील पदावलीमध्ये गृहीत धरलेला संबंध समदिक् अथवा ज्याच्या स्फटिक रचनेमध्ये केंद्रीय सममिती (प्रमाणबद्धता) आहे अशा अपारक पदार्थाकरिताच यथार्थ ठरतो. काच व निरनिराळे द्रव हे पहिल्या प्रकारात येतात, तर कॅल्साइट स्फटिक दुसऱ्या प्रकारात मोडतो. उच्च परमप्रसराच्या लेसर प्रकाश शलाकेद्वारे सुयोग्य स्फटिक उद्दिप्त केला असता पारक प्रारणामध्ये प्रगुण कंप्रतेचा प्रकाश मिळतो. या विक्रियेची परिवर्तनक्षमता २०% एवढी असू शकते. मिळालेला प्रकाश लेसर स्वरूपाचाच कलामेलित (शलाकेच्या काटच्छेदातील निरनिराळ्या बिंदूंपाशी असलेल्या कलांमध्ये निश्चित संबंध असलेला) असल्यामुळे या पद्धतीद्वारे ज्या कंप्रता सरळ लेसर क्रियेद्वारे मिळू शकत नाहीत त्या उपलब्ध करून घेता येतात.

प्रगुण कंप्रतेची शलाका निर्माण करण्याकरिता वापरलेल्या पदार्थाला (स्फटिकाला) जास्त जाडी असेल, तर त्यामधील अपस्करणामुळे (घटक कंप्रता अलग झाल्यामुळे) एक अडचण निर्माण होते. निर्माण झालेला उच्च प्रगुण कंप्रतेचा प्रकाश घटक आपल्या कंप्रतेनुसार पदार्थामधून प्रगत होतो. याचा प्रगतीचा वेग मूळ प्रकाश घटकाच्या वेगापेक्षा निराळा असतो आणि त्यामुळे आपाती प्रकाश जसा पदार्थाच्या आत शिरत जातो तसतसे निरनिराळ्या ठिकाणांवरून अथवा उगम स्थानांपासून उच्च कंप्रता प्रकाश घटक निर्माण होऊन प्रसारण पावतात. यामुळे सुरुवातीस निर्माण झालेला प्रगुण घटक व त्यानंतर काही अंतरावर निर्माण झालेला तसाच घटक यांच्या कलांमध्ये अंतर पडून त्यामध्ये भंजक व्यतिकरण होण्याचा संभव असतो. ही क्रिया टाळण्याकरिता विशेष काळजी घ्यावी लागते. KDP (पोटॅशियम डायफॉस्फेट) या स्फटिकामध्ये हे कार्य अत्यंत कल्पकतेने केले जाते. स्फटिकाचा दिक्-विन्यास असा ठेवलेला असतो की, आपाती प्रकाश शलाका त्यामध्ये ‘सामान्य’ किरण म्हणून प्रसारण पावते, तर निर्माण झालेला उच्च प्रगुण कंप्रतेचा प्रकाश असामान्य किरण म्हणून प्रगत पावतो. या दोन्ही प्रकाश शलाकांचा वेग एकच असतो आणि त्यामुळे आपोआप कलांचा सुजोड होण्याचे कार्य घडून येते. स्फटिकाला सरल विद्युत् वर्चस् अवपात लावला, तर प्रगुण कंप्रतानिर्मितीच्या कार्यास गती मिळते असे आढळते.

प्रचलीय मिश्रण : प्रगुण कंप्रतानिर्मितीच्या व्यतिरिक्त ज्या माध्यमास नैकरेषीय प्रकाशकीय गुणधर्म आहेत अशा माध्यमात दोन प्रकाश कंप्रतांचे मिश्रण होऊ शकते. या क्रियेमधून मिळणाऱ्या परिणामी कंप्रतेचा मूळ घटक कंप्रतेशी रेषीय संबंध असतो. ν₁ व ν₂ या घटक कंप्रतापासून ν₁ + ν₂ आणि ν₁ – ν₂या परिणामी कंप्रतांची निर्मिती हे या प्रकारच्या मिश्रण क्रियेचे सर्वांत सामान्यपणे आढळणारे उदाहरण आहे. या क्रियेला प्रचलीय मिश्रण क्रिया असे म्हणतात.

ज्यांच्या स्फटिकाला सममिती नाही व जी प्रकाशतः सक्रिय आहेत अशी द्रव्ये या कार्याकरिता उपयुक्त ठरतात. मिश्रण करण्याकरिता वापरलेल्या दोन्ही प्रकाश शलाका लेसरच्याच असल्या पाहिजेत असे नाही, असे आढळले आहे. एक उच्च तीव्रतेची लेसर शलाका व पाऱ्याच्या प्रज्योत दिव्यापासून मिळणारा त्या मानाने कमी तीव्रतेचा प्रकाश या दोहोंमध्ये सुद्धा अशा प्रकारचे मिश्रण होऊ शकते, हे दाखविण्यात आले आहे. हा परिणाम स्पंदित घनावस्थी किंवा अखंडित तरंग वायू लेसर [→ लेसर] या दोन्ही प्रकारे निर्माण केलेल्या प्रकाश शलाकांच्या बाबतीत मिळतो. दोन लेसर प्रकाश शलाकांचे मिश्रण करून विभेदी कंप्रतेच्या (दोन कंप्रतांच्या वजाबाकीने मिळणाऱ्या कंप्रतेच्या) द्वारे अवरक्त क्षेत्रात तर योग कंप्रतेच्या (दोन कंप्रतांच्या बेरजेने मिळणाऱ्या कंप्रतेच्या) द्वारे दृश्य अथवा जंबुपार (वर्णपटातील जांभळ्या रंगाच्या पलीकडील अदृश्य) क्षेत्रातील लेसर प्रकाश निर्माण केला जातो.

---

तीव्रता अवलंबी प्रसारण परिणाम : रेषीय सिद्धांताप्रमाणे प्रकाश तरंग जेव्हा माध्यमात प्रसारण पावतात तेव्हा तरंग वेग (माध्यमाचा प्रणमनांक म्हणजे निर्वातातील प्रकाश वेग व माध्यमातील प्रकाश वेग यांचे गुणोत्तर) आणि त्याकरिता माध्यमाचा शोषण गुणांक हे प्रकाश तीव्रतेवर अवलंबून नसतात, असे गृहीत धरलेले असते. माध्यमाची नैकरेषीय वर्तणूक लक्षात घेतली, तर प्रसारणाशी संबंधित असलेल्या वरील तिन्ही राशी तीव्रतेप्रमाणे बदलतात असे आढळते. या चलनामुळे खालील विशेष आविष्कार मिळतात.

(१) निरनिराळ्या तीव्रतांचे तरंग नैकरेषीय माध्यमातून भिन्न वेगाने प्रसारण पावतील. जर आपाती प्रकाश स्पंदाच्या स्वरूपात असेल, तर यामधील तीव्रता काही कालखंडाकरिता कालपरिवर्ती असते. अशा परिस्थितीत त्यामधील प्रथमतः मागे असलेला पण अधिक वेगाने प्रसारण पावणारा घटक, कमी वेगाने जाणाऱ्या घटकाला गाठून त्याच्या पुढेसुद्धा जाऊ शकेल. या क्रियेमुळे प्रदान तरंगाकार आदान तरंगाकारापेक्षा जास्त तीव्र होतो व काही वेळा स्पंदाचे आघात तरंगात [→ तरंग गति] रूपांतर होते.

(२) माध्यमामधून जाणाऱ्या प्रकाश शलाकेचे स्वरूप नैकविध असेल आणि तिच्यातील निरनिराळे विभाग भिन्न वेगाने प्रगत होत असतील व माध्यमाचा प्रणमनांक प्रकाश तीव्रतेनुसार वाढत असेल, तर प्रसारणामुळे शलाकेचे स्वयंकेंद्रीकरण होते. ज्या द्रायूकरिता (वायू किंवा द्रवाकरिता) कर गुणांक [→ कर परिणाम] उच्च प्रतीचा आहे अशांमध्ये हा परिणाम विशेष प्रमाणात आढळतो.

(३) नीच कंप्रतेची विद्युत् चुंबकीय क्षेत्रे माध्यमावर लावून त्यायोगे एका ठराविक तरंगलांबीच्या प्रकाशाच्या प्रसारणविषयक राशीचे नियंत्रण करून त्यामध्ये यथाप्रमाण बदल घडवून आणणे शक्य होते. या परिणामाचा उपयोग प्रकाशाद्वारा संदेशवहन करण्याकडे केला जातो [→ प्रकाशीय संदेशवहन].

(४) काही विशिष्ट शोषकद्रव्ये (ज्यांची शोषकता संपृक्त करता येते) ही सर्वसामान्यपणे सर्व आपाती प्रकाशाचे शोषण करीत असल्यामुळे ती अपारदर्शक असतात. यावर अति-उच्च तीव्रतेचा प्रकाश प्रथम टाकून त्याची शोषकता संपृक्त केली, तर ही द्रव्ये प्रकाशाकरिता पारदर्शक बनतात.

बहुविध फोटॉन शोषण परिणाम : द्रव्य आणि प्रकाशप्रारण यांच्या परस्परक्रियेमध्ये एकाच वेळी प्रकाशातील दोन फोटॉनांचे शोषण काही परिस्थितीत होण्याची शक्यता सैद्धांतिक दृष्ट्या पूर्वसूचित केली गेली होती. या प्रकारचे शोषण होण्याकरिता पदार्थाच्या ऊर्जा पातळ्यांमधील अंतरे आपाती फोटॉन ऊर्जेच्या काही पूर्णांकी पटीत असावी लागतात आणि हे ऊर्जा शोषण तद्नुरूप निवड नियमानुसार शक्य असावे लागते. लेसरच्या शोधामुळे या परिणामाचा प्रयोगाच्या साहाय्याने पडताळा पाहणे शक्य झाले आहे. एकाच क्रियेत एकाच वेळी दोन फोटॉनांचे शोषण प्रथम निओडिमियम क्लोराइडाच्या (NdCl₃) स्फटिकात आढळले. या स्फटिकाचे अवरक्त लेसर शलाकेच्या द्वारे उद्दीपन केले असता, त्यापासून मिळणारा अनुस्फुरण प्रकाश (विशिष्ट तरंगलांबीच्या प्रारणाचे शोषण करून उत्सर्जित होणारा जास्त तरंगलांबीचा प्रकाश) दृश्य वर्णपट विभागातील असतो असे आढळले.

बहुविध फोटॉन शोषण परिणामाचा अभ्यास करण्याकरिता नेहमी एकच प्रकाश शलाका वापरली जाते असे नाही. शोषक पदार्थावर एका तरंगलांबीचा प्रकाश टाकल्यामुळे त्याचे शोषण होत असताना त्यावर त्याच वेळी दुसऱ्या तरंगलांबीचा प्रकाश टाकला, तर प्राथमिक शोषण क्रियेत बदल होतो असे आढळते. या परिणामाचा उपयोग द्विफोटॉन वर्णपटविज्ञानात केला जातो. यामध्ये पदार्थावर एक नीच शक्तीचा अखंडित वर्णपटी प्रकाश पडत असताना त्यावर त्याच वेळी उच्च शक्तीचा पण बदलत्या तरंगलांबीचा एकवर्णी प्रकाशही टाकला जातो. नीच शक्तीच्या प्रकाशाकरिता पदार्थाच्या शोषण गुणांकाचे तरंगलांबीवरील अवलंबित्व नेहेमीच्याच रीतीने मोजले जाते. उच्च व नीच शक्तीच्या ज्या तरंगलांबींकरिता विशेष शोषण मिळते त्यावरून पदार्थाच्या ऊर्जापातळीविषयी माहिती मिळते. अशा प्रकारची माहिती इतर दुसऱ्या प्रकाराने मिळविणे सोपे नसते.

माध्यमामधून प्रकाशाचे प्रसारण झाले असता त्याचे अस्थितिस्थापक प्रकीर्णन (विखुरण्याची क्रिया) होऊन त्याची कंप्रता बदलते. कंप्रतेत होणारा बदल माध्यमातील रेणूंच्या कंपन तऱ्हा आणि तद्नुरूप ऊर्जा पातळ्या यांच्याशी संबंधित असतो. हा परिणाम सी. व्ही. रामन यांनी प्रथम संशोधिला. फोनॉन, पोलॅरीटॉन इ. घन पदार्थांमध्ये मिळणाऱ्या नवीन पुंजकणांबरोबर परस्परक्रिया होऊन फोटॉनांचे प्रकीर्णन होते. या प्रकराच्या संशोधनांचा समावेशही याच विभागात होतो.

स्वयंप्रेरित पारदर्शिका : प्रत्येक माध्यमाकरिता एक ठराविक लाक्षणिक कंप्रता असते. माध्यमाचा अपस्करण वक्र या कंप्रतेकरिता काही विशेष गुणधर्म दाखवितो. माध्यमामधून याच कंप्रतेच्या प्रकाशाचा स्पंद पाठविला, तर त्याचा आकार व उंची योग्य असल्यास त्याचे माध्यमामधून काही क्षीणन न होता प्रसारण होते. या प्रकारास स्वयंप्रेरित पारदर्शिका परिणाम असे म्हणतात. माध्यमाच्या अपस्करण वक्राच्या नैकरेषीय स्वरूपामुळे निर्माण होणारा हा एक परिणाम आहे.

संदर्भ : 1. Angelo, E. J. Electronic Circuits, New York, 1964.

   2. Armington, R. E. Volz, C. Introduction to Electric Circuit Analysis, New Jersey, 1961.

   3. Bloembergen, N. Non-linear Optics, New  York, 1965.

   4. Carrol, J. M. Electron Devices and Circuits, New York, 1962.

   5. Cockrell, W. D., Ed. Industrial Electronics Handbook, New York, 1958.

   6. Garbuny, M. Optical Physics, New York, 1965.

   7. Geyger, W. A. Nonlinear Magnetic Control Devices, New York, 1964.

   8. Henney, K., Ed. Radio Engineering Handbook, New York, 1959.

   9. Levi, L. Applied Optics, New York, 1968.

  10. Machol, R. E., Ed. System Engineers’ Handbook, New York, 1965.

  11. Pederson, D. O. Studer, J. J. Whinnery, J. R. Introduction to Electronic Systems, Circuits and Devices, New York, 1966.

  12. Smith, W. V. Sorokin, P.P. The  Laser, New York, 1966.

  13. Stern, J. E. Theory of Non-linear Networks and Systems, Reading, 1965.

  14. Van Heel, A. C. S. Advanced Optical Techniques, Amsterdam, 1967.

चिपळोणकर, व. त्रिं.

“