कॉम्पटन परिणाम : इलेक्ट्रॉनवरून क्ष-किरणांचे अथवा गॅमा किरणांचे प्रकीर्णन (विखुरणे) झाले असता प्रकीर्णित किरणांची तरंगलांबी वाढलेली दिसून येते या आविष्काराला कॉम्पटन परिणाम असे म्हणतात. हा परिणाम आर्थर हॉली कॉम्पटन यांना क्ष-किरणांच्या प्रयोगाच्या संबंधात १९२२ साली प्रथम आढळला व सैद्धांतिक रीत्या त्यांनी आणि त्याचवेळी स्वतंत्रपणे डेबाय यांनी तो सिद्ध केला म्हणून यूरोपमध्ये तो कॉम्पटन-डेबाय परिणाम म्हणूनही ओळखला जातो. प्रकीर्णन-कोनावर कॉम्पटन परिणाम अवलंबून असतो म्हणून तो ⇨रामन परिणामाहून भिन्न आहे. कॉम्पटन परिणामात तरंगलांबीत फरक होत असल्याने तो रॅली परिणामाहूनही (प्रकाशाच्या तरंगलांबीपेक्षा लहान असलेल्या कणांमुळे होणाऱ्या प्रकीर्णनाच्या रॅली यांनी शोधून काढलेल्या परिणामाहूनही) भिन्न आहे.
आइन्स्टाइन यांच्या प्रकाशविद्युत् परिणामाप्रमाणेच (विद्युत् निरोधित संवाहकावर प्रकाश पाडला असता त्या संवाहकाचा ॠण विद्युत् भार नाहीसा होणे वा त्याला धन विद्युत् भार प्राप्त होणे या परिणामाप्रमाणेच) या कॉम्पटन परिणामामुळे असे निश्चित झाले की, प्रारणाच्या (तरंगरूपी ऊर्जेच्या) सर्वांगीण स्पष्टीकरणाच्या दृष्टीने एकटा तरंगसिद्धांत पुरेसा नाही, तर यासाठी प्रारणाचे दुसरे स्वरूप म्हणजे प्रारण हे ऊर्जापुंजांचे (क्वांटमांचे) बनलेले असते, हेही विचारात घ्यावयास हवे. शिवाय या परिणामाचे आणखी एक महत्त्व असे आहे की, त्यावरून व त्यासारख्या इतर आविष्कारांवरून हायझेनबेर्क यांना स्वतःचे ⇨अनिश्चिततेचे तत्त्व मांडता आले.
प्रायोगिक व सैद्धांतिक स्पष्टीकरण : कार्बनासारख्या हलक्या मूलद्रव्याचा स्फटिक प्रकीर्णक म्हणून वापरला असता, आपाती (पडणाऱ्या) क्ष-किरणांच्या दिशेशी कोणताही θ हा कोन करून होणाऱ्या दिशेकडील प्रकीर्णनात कॉम्पटन परिणाम आढळतो. यासंबंधीची प्रायोगिक रचना आ. १ मध्ये आणि घडणारा परिणाम आ. २ मध्ये दाखविला आहे.
क्ष-किरणांची एक अरुंद शलाका (आ. १) स१, स२ या दोन रेखाछिद्रांतून जाऊन क या स्फटिकावर पडते व तेथे क्ष-किरणांचे प्रकीर्णन घडून, ते प्रकीर्णित किरण आयनीकरण (विद्युत् भारित अणू वा रेणू तयार करणाऱ्या) कोठीत शिरतात किंवा छायाचित्रण काचेवर पडतात. आकृती प्रतलास (पातळीस) प्रलंब अशा अक्षाभोवती क हा स्फटिक काही विशिष्ट कोनातून फिरविल्यास छायाचित्रण काचेवर वर्णपट उमटतो. वर्णपटावरून असे दिसून येते की, क्ष-अगर गॅमा-किरणांच्या
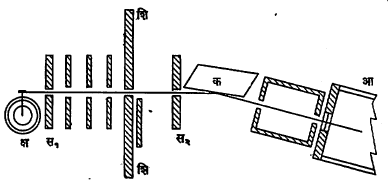
(क्ष-किरणांहून कमी तरंगलांबी असलेल्या किरणांच्या) कोणत्याही विशिष्ट v कंप्रतेच्या (दर सेकंदास होणाऱ्या कंपन संख्येच्या) व λ तरंगलांबीच्या प्रारणामुळे λ´ या वाढलेल्या तरंगलांबीची (कंप्रता v´ ) रेषा मिळते व या दोन तरंगलांब्यांतील फरक (λ´ – λ) म्हणजेच कॉम्पटन बदल, समी. (१) मध्ये दाखविल्याप्रमाणे प्रकीर्णन कोन θ बरोबर वाढत जातो.
|
λ´– λ =∆λ = |
c |
– |
c |
= |
h |
( 1 – cos θ ) |
|
v ´ |
v |
M0c |
= 0.0242 ( 1 – cos θ ) ….. (१)
या समीकरणात c हा प्रकाशवेग असून mo हे स्थिर इलेक्ट्रॉनाचे वस्तुमान आहे व h हा प्लांक विश्वस्थिरांक
आहे. क्ष-किरणरूपी फोटॉन (प्रकाशीय ऊर्जेची सर्वांत लहान राशी म्हणजे पुंज किंवा क्वांटम) व स्फटिकातील इलेक्ट्रॉन e यांच्या टकरीस ऊर्जा आणि संवेग (वस्तुमान गुणिले वेग) यांच्या अक्षय्यतेचा सिद्धांत लागू करून हे समीकरण सिद्ध करता येते तसे करताना फोटॉनांसही संवेग असतो असे गृहित धरावे लागते आणि या संवेगाचे मूल्य
|
P = |
hv |
= |
h |
या समीकरणाने दिले जाते. समी. (१) ची सिद्धता पुढे |
|
c |
λ |
थोडक्यात दर्शविली आहे.
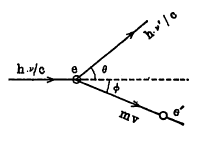
प्रकीर्णित इलेक्ट्रॉनाचा (आ. २) वेग v समजल्यास व प्रकीर्णित फोटॉन आणि इलेक्ट्रॉन यांच्या प्रकीर्णनानंतरच्या दिशा मूळ फोटॉनाच्या दिशेशी अनुक्रमे θ व φ हे कोन करतात असे समजल्यास ऊर्जेच्या अक्षय्यतेचा परिणाम म्हणून
hv + moc2 = mc2 + hv´ … … … (२)
हे समीकरण मिळते mc2 ही इलेक्ट्रॉनाची टकरीनंतरची ऊर्जा आहे. तसेच संवेगाच्या अक्षय्यतेच्या तत्त्वानुसार त्याच्या घटकासंबंधी पुढील समीकरण मिळते.
hv /c = (hv ´/c) cos θ + Pecos φ } … … (३)
(hv´/c) sin θ = Pe sin φ }
यात pe हा इलेक्ट्रॉनाचा टकरीनंतरचा संवेग आहे (Pe = m v). या (२) व (३) समीकरणांवरून गणितकृत्य करता समी. (१) मिळते. टकरीमुळे प्राप्त झालेल्या ऊर्जेमुळे इलेक्ट्रॉन अणूमधून बाहेर फेकला जातो. अशा इलेक्ट्रॉनास कॉम्पटन इलेक्ट्रॉन अथवा प्रतिक्षेप (मागे उलटलेला) इलेक्ट्रॉन म्हणतात. वरील उपपत्तीत इलेक्ट्रॉनाचे अणूशी बंधन करणाऱ्या प्रेरणा विचारात घेतलेल्या नाहीत, हे येथे लक्षात घेणे आवश्यक आहे. याचे कारण असे की, हलक्या अणूमध्ये अणूच्या बाहेरील कक्षांतील इलेक्ट्रॉनांची बंधन-ऊर्जा क्ष-किरणाच्या ऊर्जेच्या मानाने फार थोडी व म्हणून उपेक्षणीय मानता येते. याच्याच बरोबर उलट परिस्थिती दृश्य प्रकाशाचा ऊर्जाकण वापरल्यास असते व म्हणून दृश्य प्रकाश किरण हे कॉम्पटन परिणाम दाखवित नाहीत. कॉम्पटन यांच्या स्वतःच्या व नंतर ड्यूमाँड व कर्कपॅट्रिक यांच्या प्रयोगांनी समी. (१) ची सत्यता सिद्ध झाली. या प्रयोगांत आढळलेला कॉम्पटन परिणाम अनेक टकरींमुळे घडून आलेला ‘सरासरी परिणाम’ होता व त्यावरून एकच एक टकरीमुळे होणाऱ्या संवेगबदलाबद्दल काहीच माहिती मिळू शकली नाही. पण ती माहिती विल्सन बाष्पकोठी (विल्सन यांनी शोधून काढलेली आर्द्र हवायुक्त कोठी) वापरून मिळणाऱ्या पथांच्या छायाचित्रांवरून मिळू शकते (या कोठीत उच्च वेगयुक्त कण व हवेचे रेणू यांच्या टकरींमुळे निर्माण झालेल्या आयनांवर जलबिंदू साचून कणांचा मार्ग छायाचित्रित करता येतो.) गायगर व बेटे यांनी गणिताच्या साहाय्याने प्रकीर्णित फोटॉन आणि प्रतिक्षेप इलेक्ट्रॉन एकाच वेळी निर्माण होतात हे दाखवून दिले. समी. (१) मध्ये दिलेले ∆λ चे मूल्य, इलेक्ट्रॉनास द ब्रॉग्ली यांचे द्रव्यतरंग (अणू, रेणू किंवा इलेक्ट्रॉन, प्रोटॉन वगैरे सूक्ष्म द्रव्यकणांना तरंगांप्रमाणे असलेले) गुणधर्म लागू करून तरंग यामिकीच्या (द्रव्यतरंगांना लागू पडणाऱ्या प्रेरणाविज्ञानाच्या) साहाय्यानेही मिळू शकते.
रूढ भौतिकीनुसार प्रारणाचे प्रकीर्णन सर्व दिशांना सारखे व्हावयास हवे (म्हणजे आपाती प्रारणाच्या आणि त्या विरुद्ध अशा दिशांस सममित असे प्रकीर्णनाचे वितरण असावे) व प्रारणाची तरंगलांबी बदलू नये असे जे. जे. टॉमसन यांनी प्रतिपादिले होते पण प्रखर क्ष-किरण व गॅमा किरण यांच्याबाबतीत ऊर्जाकणांची संख्या व ऊर्जा ही प्रारणाच्या आपाती दिशेकडे अधिक असतात व मूळच्या कणाची ऊर्जा वाढेल त्या प्रमाणात त्या अधिकाधिक होत जातात. म्हणून वितरण असममित होते. क्लाइन व निशिना यांनी ⇨सापेक्षता सिद्धांतावर आधारलेल्या डिरॅक यांच्या तरंग यामिकीच्या समीकरणानुसार केलेले वितरणाचे प्रतिपादन सर्वांत जास्त यशस्वी ठरले आहे.
विशिष्ट कोन करून होणाऱ्या प्रकीर्णित प्रारणांच्या तीव्रता गणिताने काढता येतात अशा प्रकारे गणितक्रियेने काढलेली मूल्ये प्रायोगिक मूल्यांशी फोटॉनांच्या ऊर्जामूल्यांच्या विस्तृत भागात जुळती येतात. या संबंधात हॉफस्टॅडर व मॅकिंटायर यांनी आणि १९५२ मध्ये फोएलकर तसेच कोएन्सगेन यांनी उच्च ऊर्जा असलेले ऊर्जाकण वापरून केलेल्या प्रयोगांचा विशेष उल्लेख करावयास हवा.
कॉम्पटन प्रकीर्णनात सर्वसाधारणपणे एकच ऊर्जाकण प्रकीर्णित होत असला, तरी क्वचित दोन ऊर्जाकणांचेही प्रकीर्णन होऊ शकते. या घटनेची शक्यता सापेक्षतेवर आधारलेल्या ⇨पुंजयामिकीने आधीच दर्शविली होती. समी. (१) स्थापन करताना अणूमधील इलेक्ट्रॉन सुरुवातीस स्थिर आहेत असे गृहित धरले होते, परंतु ते स्थिर नसून अणुगर्भाभोवती स्वतःच्या कक्षांत वेगाने भ्रमण करीत असतात आणि म्हणून सुरुवातीस त्यांस संवेग असतो असे मानावयास हवे. ड्यूमाँड व कर्कपॅट्रिक यांच्या मते या घटनेमुळे कॉम्पटन-तरंगलांबी बदलावर आणखी एक बदल अध्यारोपित होतो (लादला जातो). या दुसऱ्या बदलास डॉप्लर बदल म्हणता येईल व त्याच्यामुळे इलेक्ट्रॉनाच्या मूळ संवेगाच्या दिशेप्रमाणे कॉम्पटन बदल रुंदावेल अगर बारीक होईल. ही गोष्ट सत्य आहे असे तत्संबंधीच्या वर्णपटरेषा तपासताना ड्यूमाँड व कर्कपॅट्रिक यांस आढळून आले. अणूमधील इलेक्ट्रॉन एकसारखे वेगाने भ्रमण करीत असतात, या गोष्टीचा हा अप्रत्यक्ष पुरावाच मानता येईल.
अनुप्रयोग : प्रायोगिक भौतिकीतील एक अवघड समस्या म्हणजे एकच तरंगलांबी व ऊर्जा असलेले गॅमा किरण प्राप्त करून घेणे व प्रयोगाच्या जरूरीप्रमाणे ते ऊर्जामूल्य बदलून आपणास हवे असलेले निरनिराळ्या ऊर्जामूल्यांचे (व तत्तुल्य तरंगलांबीचे) गॅमा किरण मिळविणे ही होय. ही बदलती ऊर्जामूल्ये का लागतात हे पुढील उदाहरणावरून स्पष्ट होईल : १० Mev पेक्षा (Mev म्हणजे मिलियन इलेक्ट्रॉन व्होल्ट, ऊर्जेचे एक एकक) कमी ऊर्जा असलेल्या गॅमा किरणांचा उपयोग अणूतील बद्ध इलेक्ट्रॉनांना क्षोभित करून अणुगर्भाच्या रचनेचा अभ्यास करण्याकडे होतो, सु. १० ते १५० Mev ऊर्जा असलेल्या गॅमा किरणांचा उपयोग अणुगर्भीय विक्रिया घडवून आणण्याकडे, तर १५० Mev पेक्षा अधिक ऊर्जा असलेल्या गॅमा किरणांचा उपयोग त्यांचा पदार्थावर मारा करून मूलकणांच्या उत्पत्तीचा अभ्यास करण्याकडे होतो. अशा बदलत्या ऊर्जा टॅंडन व मॅकिंटायर यांनी ॲल्युमिनियमाचा पत्रा प्रकीर्णक म्हणून वापरून व त्यावरून गॅमा किरणांचे प्रकीर्णन करून मिळविल्या. यासाठी कोबाल्ट (६०) या किरणोत्सर्गी (भेदक कण वा किरण उत्सर्जित करणाऱ्या) पदार्थापासून निघणारे गॅमा किरण त्यांनी वापरले आणि त्यांची मूळची ऊर्जा कॉम्पटन प्रकीर्णनाने कमी केली. प्रकीर्णन कोन बदलता ठेवून प्रकीर्णित गॅमा किरणांची ऊर्जा बदलती ठेवली. ॲल्युमिनियम प्रकीर्णकाचा आकार असा ठेवला की, त्यावरून प्रकीर्णित गॅमा किरण लक्ष्यावर संकेंद्रित (एका बिंदूत एकत्रित) करता येतील. अणुगर्भीय विक्रियकापासून निर्माण झालेले गॅमा किरणही कॉम्पटन प्रकीर्णनाचा उपयोग करून काही प्रयोगशाळांमध्ये शास्त्रज्ञांनी वापरले आहेत. याच पद्धतीचा उपयोग रिचर्ड मिलबर्न यांनी ध्रुवित (विशिष्ट प्रतलात कंपन पावत असलेल्या) गॅमा किरणांची शलाका मिळविण्याकडे केला. अशा तऱ्हेने ही पद्धत म्हणजे शास्त्रज्ञांस उपलब्ध झालेले एक उपयुक्त हत्यारच ठरले आहे.
आतापर्यंत इलेक्ट्रॉनांमुळे घडणारे फोटॉनांच्या (गॅमा किरणांच्या) प्रकीर्णनाचे वर्णन झाले तथापि इतर मूलकणांशी, उदा. प्रोटॉनांशी, फोटॉनांची याच तऱ्हेची क्रिया घडून येण्याची शक्यता नाकारता येत नाही. किंबहुना कॉम्पटन परिणामाप्रमाणे प्रोटॉनांकडून प्रकीर्णित झालेले फोटॉन उच्च ऊर्जा भौतिकीच्या प्रयोगात आढळले आहेत. प्रोटॉनाचे वस्तुमान इलेक्ट्रॉनाच्या वस्तुमानापेक्षा बरेच मोठे असल्याने, त्यास इलेक्ट्रॉनापेक्षा बराच कमी संवेग प्राप्त होतो आणि कॉम्पटन-तरंगलांबी बदलही त्याच मानाने लहान असतो.
वरील विवेचनावरून प्रारण व द्रव्य यांमधील परस्परक्रियेचा नीट उलगडा होण्यास कॉम्पटन प्रकीर्णनाचे अमोल साहाय्य झाले, हे स्पष्ट होईल.
संदर्भ : 1. Compton, A. H Allison, S. K. X-rays in Theory and Experiment, New York, 1960.
2.Kaplan, I. Nuclear Physics, Tokyo, 1964.
3.Richtmeyer, F. K. Kennard, E. H. Introduction to Modern Physics, Tokyo, 1964.
भावे, श्री. द.
“